四川省成都邛崃市2020届九年级上学期摸底（期中）考试数学试题

四川省成都邛崃市2020届九年级上学期摸底（期中）考试数学试题

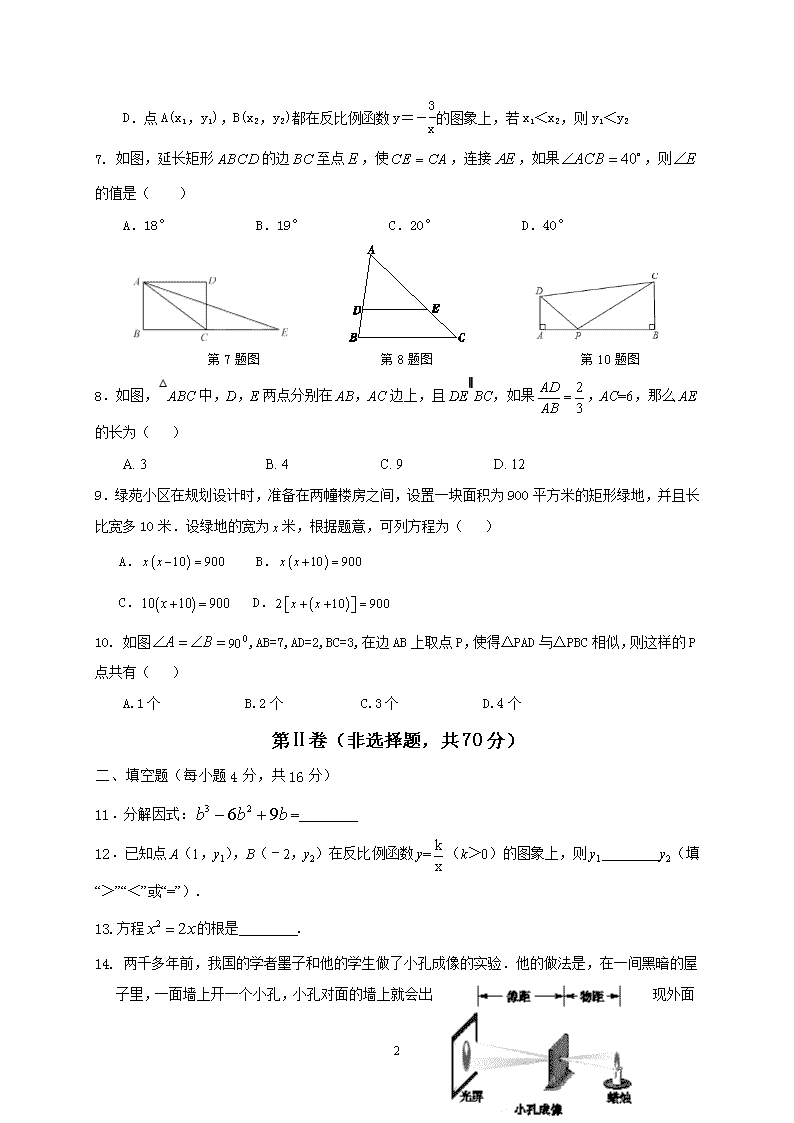
1 2019~2020 学年度上期九年级数学半期质量监测试题 数 学 A 卷（共 100 分） 一．选择题（共 10 小题，满分 30 分，每小题 3 分） 1. 如图，是由 4 个相同小正方体组合而成的几何体，它的左视图是（ ） A． B． C． D． 2. 函数 y= x 2x－1 有意义的 x 的取值范围是（ ） A．x≥0 B．x≠1 2 C．x≥0 且 x≠1 2 D．一切实数 3．七年级（1）班与（2）班各选出 20 名学生进行英文打字比赛，通过对参赛学生每分钟输入的单 词个数进行统计，两班成绩的平均数相同，（1）班成绩的方差为 17.5，（2）班成绩的方差为 15，由 此可知（ ） A．（1）班比（2）班的成绩稳定 B．（2）班比（1）班的成绩稳定 C．两个班的成绩一样稳定 D．无法确定哪班的成绩更稳定 4．已知 ，则 的值是（ ） A． B． C．1 D． 5．若关于 x 的方程 2 9 04x x a    有两个不相等的实数根，则实数 a 的取值范围是（ ） A. 2a≥ B. 2a ≤ C. 2a＞ D. 2a＜ 6．对于反比例函数 y＝－3 x ，下列说法不正确的是（ ） A．图象经过点(1，－3) B．图象分布在第二、四象限 C．当 x＞0 时，y 随 x 的增大而增大 2 D．点 A(x1，y1)，B(x2，y2)都在反比例函数 y＝－3 x 的图象上，若 x1＜x2，则 y1＜y2 7. 如图，延长矩形 ABCD 的边 BC 至点 E ，使CE CA ，连接 AE ，如果 40ACB   ，则 E 的值是（ ） A．18° B．19° C．20° D．40° 第 7 题图 第 8 题图 第 10 题图 8．如图，△ABC 中，D，E 两点分别在 AB，AC 边上，且 DE∥BC，如果 2 3 AD AB  ，AC=6，那么 AE 的长为（ ） A. 3 B. 4 C. 9 D. 12 9．绿苑小区在规划设计时，准备在两幢楼房之间，设置一块面积为 900 平方米的矩形绿地，并且长 比宽多 10 米．设绿地的宽为 x 米，根据题意，可列方程为（ ） A．  10 900x x   B．  10 900x x   C．  10 10 900x   D．  2 10 900x x     10. 如图 900 BA ,AB=7,AD=2,BC=3,在边 AB 上取点 P，使得△PAD 与△PBC 相似，则这样的 P 点共有（ ） A.1 个 B.2 个 C.3 个 D.4 个 第Ⅱ卷（非选择题，共 70 分） 二、填空题（每小题 4 分，共 16 分） 11．分解因式： 3 26 9b b b  = 12．已知点 A（1，y1），B（﹣2，y2）在反比例函数 y= k x （k＞0）的图象上，则 y1 y2（填“＞”“＜” 或“=”）. 13.方程 2 2x x 的根是 . 14. 两千多年前，我国的学者墨子和他的学生做了小孔成像的实验．他的做法是，在一间黑暗的屋 子里，一面墙上开一个小孔，小孔对面的墙上就会出 现外面 3 景物的倒像．小华在学习了小孔成像的原理后，利用如下装置来验证小孔成像的现象．已知一根 点燃的蜡烛距小孔 20cm，光屏在距小孔 30cm 处，小华测量了蜡烛的火焰高度为 2cm，则光屏 上火焰所成像的高度为 cm． 三、解答题（本大题共 6 个小题，共 54 分） 15．（本小题满分 12 分，每题 6 分） （1）解方程： 5 42 3 3 2 x x x    ． （2）先化简，再求值：（ ﹣ ）÷ ，其中 x= ． 16．（本小题满分 6 分）已知 2 5 4 0x x   ，求代数式 ( 2)( 2) (2 1)( 2)x x x x     的值． 17．（本小题满分 8 分）有 A，B 两个黑布袋，A 布袋中有两个完全相同的小球，分别标有数字 1 和 2．B 布袋中有三个完全相同的小球，分别标有数字-1，-2 和 2．小明从 A 布袋中随机取出一个小球，记 录其标有的数字为 x，再从 B 布袋中随机取出一个小球，记录其标有的数字为 y，这样就确定点 Q 的一个坐标为（x，y）． （1）用列表或画树状图的方法写出点 Q 的所有可能坐标； （2）求点 Q 落在直线 y=x-3 上的概率． 4 18．（本小题满分 8 分） 如图，在平面直角坐标系中，△ABC 的三个顶点坐标分别为 A(－2，1)，B(－1，4)，C(－3，2)． (1)画出△ABC 关于 y 轴对称的图形△A1B1C1，并直接写出点 C1 的坐标； (2)以原点 O 为位似中心，位似比为 1∶2，在 y 轴的左侧，画出△ABC 放大后的图形△A2B2C2， 并直接写出点 C2 的坐标； (3)如果点 D(a，b)在线段 AB 上，请直接写出经过(2)的变化后 D 的对应点 D2 的坐标． 19.(本小题满分 10 分) 如图，四边形 ABCD 是平行四边形，点 A（1，0），B（3，1），C（3，3）．反 比例函数 y= m x （x＞0）的函数图象经过点 D，点 P 是一次函数 y=kx＋3－3k（k≠0）的图象与该反 比例函数图象的一个公共点． （1）求反比例函数的解析式； （2）通过计算，说明一次函数 y=kx＋3－3k（k≠0）的 图象一定过点 C； （3）对于一次函数 y=kx＋3－3k（k≠0），当 y 随 x 的增 大而增大时，确定点 P 的横坐标的取值范围（不必写出 过程）． 5 20．（本小题满分 10 分）如图，在 Rt△ABC 中，∠ACB＝90°，AC＝6cm，BC＝8cm.动点 M 从点 B 出发，在 BA 边上以每秒 3cm 的速度向定点 A 运动，同时动点 N 从点 C 出发，在 CB 边上以每秒 2cm 的速度向点 B 运动，运动时间为 t 秒 0＜t＜10 3 ，连接 MN. (1)若△BMN 与△ABC 相似，求 t 的值； (2)连接 AN，CM，若 AN⊥CM，求 t 的值． B 卷（共 50 分） 一、填空题（每小题 4 分，共 20 分） 21．在矩形 ABCD 中，由 9 个边长均为 1 的正方形组成的“L 型”模板如图放置，此时量得 CF=3,则 BC 边的长度为 . 21 题图 22 题图 22．如图，在平面直角坐标系 xOy 中，点 D 为直线 2y x 上且在第一象限内的任意一点， 1DA ⊥ x 轴于点 1A ，以 1DA 为边在 1DA 的右侧作正方形 1 1 1A B C D ；直线 1OC 与边 1DA 交于点 2A ，以 2DA 为边 在 2DA 的右侧作正方形 2 2 2A B C D ；直线 2OC 与边 1DA 交于点 3A ，以 3DA 为边在 3DA 的右侧作正方形 3 3 3A B C D ，……，按这种方式进行下去，则直线 1OC 对应的函数表 达式为 ，直线 3OC 对应的函数表达式为 . 23．若关于 x 的分式方程 3 11 x a x x    无解，则 a  . 24．如图，在△ABC 中，AB=AC=10，BC=16，D 和 M 分别是 BC、AC 边上的动点，则 AD+DM 的最小值 是 . 6 24 题图 25 题图 25．如图，点 M 是反比例函数 y= 在第一象限内图象上的点，作 MB⊥x 轴于 B．过点 M 的第一条直 线交 y 轴于点 A1，交反比例函数图象于点 C1，且 A1C1= A1M，△A1C1B 的面积记为 S1；过点 M 的第二 条直线交 y 轴于点 A2，交反比例函数图象于点 C2，且 A2C2= A2M，△A2C2B 的面积记为 S2；过点 M 的 第三条直线交 y 轴于点 A3，交反比例函数图象于点 C3，且 A3C3= A3M，△A3C3B 的面积记为 S3；以此 类推…；S1+S2+S3+…+S6= ． 二、解答题（本大题共 3 个小题，共 30 分） 26．（本小题满分 8 分）已知关于 x 的一元二次方程（m﹣2）x2+（2m+1）x+m=0 有两个实数根 x1，x2．（1） 求 m 的取值范围．（2）若|x1|=|x2|，求 m 的值及方程的根． 27．（本小题满分 10 分） 如图①，△ABC 与△CDE 是等腰直角三角形，直角边 AC、CD 在同一条直线上，点 M、N 分别是斜边 AB、DE 的中点，点 P 为 AD 的中点，连接 AE、BD． （1）猜想 PM 与 PN 的数量关系及位置关系，请直接写出结论； （2）现将图①中的△CDE 绕着点 C 顺时针旋转α（0°＜α＜90°），得到图②，AE 与 MP、BD 分别 交于点 G、H．请判断（1）中的结论是否成立？若成立，请证明；若不成立，请说明理由； （3）若图②中的等腰直角三角形变成直角三角形，使 BC=kAC，CD=kCE，如图③，写出 PM 与 PN 的 数量关系，并加以证明． 7 28．（本小题满分 12 分）如图，在平面直角坐标系中，直线 l 平行 x 轴，交 y 轴于点 A，第一象限 内的点 B 在 l 上，连结 OB，动点 P 满足∠APQ=90°，PQ 交 x 轴于点 C． （1）当动点 P 与点 B 重合时，若点 B 的坐标是（2，1），求 PA 的长． （2）当动点 P 在线段 OB 的延长线上时，若点 A 的纵坐标与点 B 的横坐标相等，求 PA：PC 的值． （3）当动点 P 在直线 OB 上时，点 D 是直线 OB 与直线 CA 的交点，点 E 是直线 CP 与 y 轴的交点，若 ∠ACE=∠AEC，PD=2OD，求 PA：PC 的值． 8 2019~2020 学年度上期九年级数学半期质量监测 数学试题参考答案 全卷总分 150 分 考试时间 120 分钟 A 卷（共 100 分） 一、选择题（每小题 3 分，共 30 分） 1. C 2. C 3．B 4． D 5． C 6． D 7. C 8． B 9． B 10. C 二、填空题（每小题 4 分，共 16 分） 11． 2( 3)b b  12． ＞ 13. x1＝0，x2＝2 14. 3 三、解答题（本大题共 6 个小题，共 54 分） 15．（本小题满分 12 分，每题 6 分） （1） 解：去分母，得：x（3x－2）＋5（2x－3）＝4（2x－3）（3x－2）， 化简，得：7x2－20x＋13＝0， 解得：x1＝1， 2 13 7x  经检验知：x1，x2 是原方程的根。 （2） 解：原式=（ ﹣ ）• = • = • = ， 当 x= 时，原式= = ． 16．（本小题满分 6 分） 解： ( 2)( 2) (2 1)( 2)x x x x     = 2 24 (2 5 2)x x x    = 2 24 2 5 2x x x    = 2 5 6x x   ． 9 ∵ 2 5 4 0x x   ， ∴ 2 5 4x x  ． ∴ 原式= 2( 5 ) 6 4 6 10x x        ．… 17．（本小题满分 8 分） 解：（1）树状图如下： 或列表如下： ∴Q 点的所有可能是: Q（1，-1）；Q（1，2）；Q（1，-2）；Q（2，-1）；Q（2，2）；Q（2，-2）． （2）∵只有 Q（1，-2），Q（2，-1）在直线 y=x-3 上， ∴点 Q 落在直线 y=x-3 上的概率为： 2 6 = 1 3 18．（本小题满分 8 分） 解：(1)如图所示，点 C1 的坐标是(3，2)；(3 分) (2)如图所示，点 C2 的坐标是(－6，4)；(6 分) (3)点 D2 的坐标是(2a，2b)．(8 分) ． 19.(本小题满分 10 分) 解：（1）∵四边形 ABCD 是平行四边形，∴AD=BC。 ∵B（3，1），C（3，3），∴BC⊥x 轴，AD=BC=2。 而 A 点坐标为（1，0），∴点 D 的坐标为（1，2）。 ∵反比例函数 y= m x （x＞0）的函数图象经过点 D（1，2）， 10 ∴2= m 1 。∴m=2。∴反比例函数的解析式为 y= 2 x 。……………………………4 分 （2）当 x=3 时，y=kx＋3－3k=3， ∴一次函数一次函数 y=kx+3-3k（k≠0）的图象一定过点 C。……………………………7 分 （3）设点 P 的横坐标为 a，则 a 的范围为 2 3 ＜a＜3。……………………………10 分 20．（本小题满分 10 分） 解：(1)∵∠ACB＝90°，AC＝6cm，BC＝8cm， ∴BA＝ 62＋82＝10(cm)． 由题意得 BM＝3tcm，CN＝2tcm， ∴BN＝(8－2t)cm. 当△BMN∽△BAC 时，BM BA ＝BN BC ， ∴3t 10 ＝8－2t 8 ， 解得 t＝20 11 ； 当△BMN∽△BCA 时，BM BC ＝BN BA ， ∴3t 8 ＝8－2t 10 ，解得 t＝32 23.……………………………5 分 综上所述，△BMN 与△ABC 相似时，t 的值为20 11 或32 23 ； (2)如图，过点 M 作 MD⊥CB 于点 D. ∴∠BDM＝∠ACB＝90°. 又∵∠B＝∠B， ∴△BDM∽△BCA， ∴DM AC ＝BD BC ＝BM BA. ∵AC＝6cm，BC＝8cm，BA＝10cm，BM＝3tcm， ∴DM＝9 5tcm，BD＝12 5 tcm， ∴CD＝ 8－12 5 t cm. ∵AN⊥CM，∠ACB＝90°， ∴∠CAN＋∠ACM＝90°，∠MCD＋∠ACM＝90°， 11 ∴∠CAN＝∠MCD. ∵MD⊥CB， ∴∠MDC＝∠ACB＝90°， ∴△CAN∽△DCM， ∴AC CD ＝CN DM ， ∴ 6 8－12 5 t ＝2t 9 5t ， 解得 t＝13 12.……………………………10 分 B 卷（共 50 分） 一、填空题（每小题 4 分，共 20 分） 21． 7 22． 2 3y x 14 15y x 23． -2 或 1 24． 25． 255 512 二、解答题（本大题共 3 个小题，共 30 分） 26．（本小题满分 8 分） 解：（1）由题意得：△≥0 且 m﹣2≠0， ∴（2m+1）2﹣4m（m﹣2）≥0 解得 m≥﹣ 且 m≠2 （2）由题意得有两种情况： ①当 x1=x2，则△=0，所以 m=﹣ ，x1=x2=﹣ × = ． ②当 x1=﹣x2 时，则 x1+x2=0．，所以 m=﹣ ， 因为 m≥﹣ 且 m≠2，所以此时方程无解． 综上所述，m=﹣ ，x1=x2= ． 27．（本小题满分 10 分） 解：（1）PM=PN，PM⊥PN，理由如下： 12 ∵△ACB 和△ECD 是等腰直角三角形，∴AC=BC，EC=CD，∠ACB=∠ECD=90°． 在△ACE 和△BCD 中 ， ∴△ACE≌△BCD（SAS），……………………………2 分 ∴AE=BD，∠EAC=∠CBD， ∵点 M、N 分别是斜边 AB、DE 的中点，点 P 为 AD 的中点， ∴PM= BD，PN= AE，∴PM=PM，………………………………………3 分 ∵PM∥BD，PN∥AE，AE⊥BD， ∴∠NPD=∠EAC，∠MPA=∠BDC，∠EAC+∠BDC=90°， ∴∠MPA+∠NPC=90°， ∴∠MPN=90°，即 PM⊥PN；…………………………4 分 （2）∵△ACB 和△ECD 是等腰直角三角形， ∴AC=BC，EC=CD，∠ACB=∠ECD=90°． ∴∠ACB+∠BCE=∠ECD+∠BCE． ∴∠ACE=∠BCD． ∴△ACE≌△BCD．……………………………………5 分 ∴AE=BD，∠CAE=∠CBD． 又∵∠AOC=∠BOE，∠CAE=∠CBD，∴∠BHO=∠ACO=90°． ∵点 P、M、N 分别为 AD、AB、DE 的中点， ∴PM= BD，PM∥BD；PN= AE，PN∥AE． ∴PM=PN．……………………………………………………………… ………6 分 ∴∠MGE+∠BHA=180°． ∴∠MGE=90°． ∴∠MPN=90°． ∴PM⊥PN．……………………………………………………………………7 分 （3）PM=kPN ∵△ACB 和△ECD 是直角三角形，∴∠ACB=∠ECD=90°． 13 ∴∠ACB+∠BCE=∠ECD+∠BCE．∴∠ACE=∠BCD． ∵BC=kAC，CD=kCE，∴ =k． ∴△BCD∽△ACE．…………………………………………9 分 ∴BD=kAE． ∵点 P、M、N 分别为 AD、AB、DE 的中点， ∴PM= BD，PN= AE． ∴PM=kPN．………………………………………………………………10 分 28．（本小题满分 12 分） 解：（1）∵点 P 与点 B 重合，点 B 的坐标是（2，1）， ∴点 P 的坐标是（2，1）． ∴PA 的长为 2．……………………………2 分 （2）过点 P 作 PM⊥x 轴，垂足为 M，过点 P 作 PN⊥y 轴，垂足为 N，如图 1 所示． ∵点 A 的纵坐标与点 B 的横坐标相等， ∴OA=AB． ∵∠OAB=90°， ∴∠AOB=∠ABO=45°． ∵∠AOC=90°， ∴∠POC=45°． ∵PM⊥x 轴，PN⊥y 轴， ∴PM=PN，∠ANP=∠CMP=90°． ∴∠NPM=90°． ∵∠APC=90°． ∴∠APN=90°﹣∠APM=∠CPM． 在△ANP 和△CMP 中， ∵∠APN=∠CPM，PN=PM，∠ANP=∠CMP， ∴△ANP≌△CMP． ∴PA=PC． 14 ∴PA：PC 的值为 1：1．……………………………6 分 （3）①若点 P 在线段 OB 的延长线上， 过点 P 作 PM⊥x 轴，垂足为 M，过点 P 作 PN⊥y 轴，垂足为 N， PM 与直线 AC 的交点为 F，如图 2 所示． ∵∠APN=∠CPM，∠ANP=∠CMP， ∴△ANP∽△CMP． ∴ ． ∵∠ACE=∠AEC， ∴AC=AE． ∵AP⊥PC， ∴EP=CP． ∵PM∥y 轴， ∴AF=CF，OM=CM． ∴FM= OA． 设 OA=x， ∵PF∥OA， ∴△PDF∽△ODA． ∴ ∵PD=2OD， ∴PF=2OA=2x，FM= x． ∴PM= x． ∵∠APC=90°，AF=CF， ∴AC=2PF=4x． ∵∠AOC=90°， ∴OC= x． ∵∠PNO=∠NOM=∠OMP=90°， ∴四边形 PMON 是矩形． 15 ∴PN=OM= x． ∴PA：PC=PN：PM= x： x= ．……………………………9 分 ②若点 P 在线段 OB 的反向延长线上， 过点 P 作 PM⊥x 轴，垂足为 M，过点 P 作 PN⊥y 轴，垂足为 N， PM 与直线 AC 的交点为 F，如图 3 所示． 同理可得：PM= x，CA=2PF=4x，OC= x． ∴PN=OM= OC= x． ∴PA：PC=PN：PM= x： x= ．……………………………12 分 综上所述：PA：PC 的值为 或 ．