人教版九年级数学上册期中、期末检测数学试卷及答案【精品16套】,高分必备
人教版九年级数学上册
期中、期末检测数学试卷及答案【精品 16 套】,高分必备
九年级上册期中考试数学试卷附参考答案
(考试形式:闭卷 全卷共两大题 24 小题 卷面满分:120 分 考试时间:120 分钟)
一、选择题(在各小题给出的四个选项中,只有一项是符合题目要求的,请在答题卡上指定的位置填涂符合要求的选项
前面的字母代号。本大题共 15 题,每题 3 分,计 45 分)
1.在同一时刻的阳光下,小明的影子比小强的影子长,那么在同一路灯下 ( )
A.小明的影子比小强的影子长 B.小明的影子比小强的影子短
C.小明的影子和小强的影子一样长 D.无法判断谁的影子长
2.下列图形中,表示两棵小树在同一时刻阳光下的影子的图形可能是( )
3.关于 x 的一元二次方程 01)1( 22 axxa 有一个根为 0,则 a 的值是( )
A.±1 B.-1 C.1 D.0
4.不能判定四边形 ABCD 是平行四边形的条件是( )
A.∠A=∠C ∠B=∠D B.AB∥CD AD=BC C.AB∥CD ∠A=∠C D.AB∥CD AB=CD
5.三角形两边长分别为 3 和 6,第三边是方程 2 6 8 0x x 的解,则这个三角形的周长是( )
A. 11 B. 13 C. 11 或 13 D. 不能确定
6.如图,已知 MB=ND,∠MBA=∠NDC,下列哪个条件不能判定△MAB≌△NCD.
( )A.∠M=∠N B.AB=CD C.AM=CN D.AM∥CN
7.顺次连结等腰梯形各边中点得到的四边形是 ( )
A、矩形 B、菱形 C、正方形 D、平行四边形( )
8.用配方法解方程 2x 2 + 3 = 7x 时,方程可变形为( )
A.(x – 7
2
)2 = 37
4
B.(x – 7
2
)2 = 43
4
C.(x – 7
4
)2 = 1
16
D.(x – 7
4
)2 = 25
16
9.摄影兴趣小组的学生,将自己拍摄的照片向本组其他成员各赠送一张,全组共互赠了 182 张,若全组
有 x 名学生,则根据题意列出的方程是( )
A.x(x+1)=182 B.x(x-1)=182
�
N
�
M
�
D
�
C
�
B
�
A
E
A
C
D
B
C.2x(x+1)=182 D.0.5x(x-1)=182
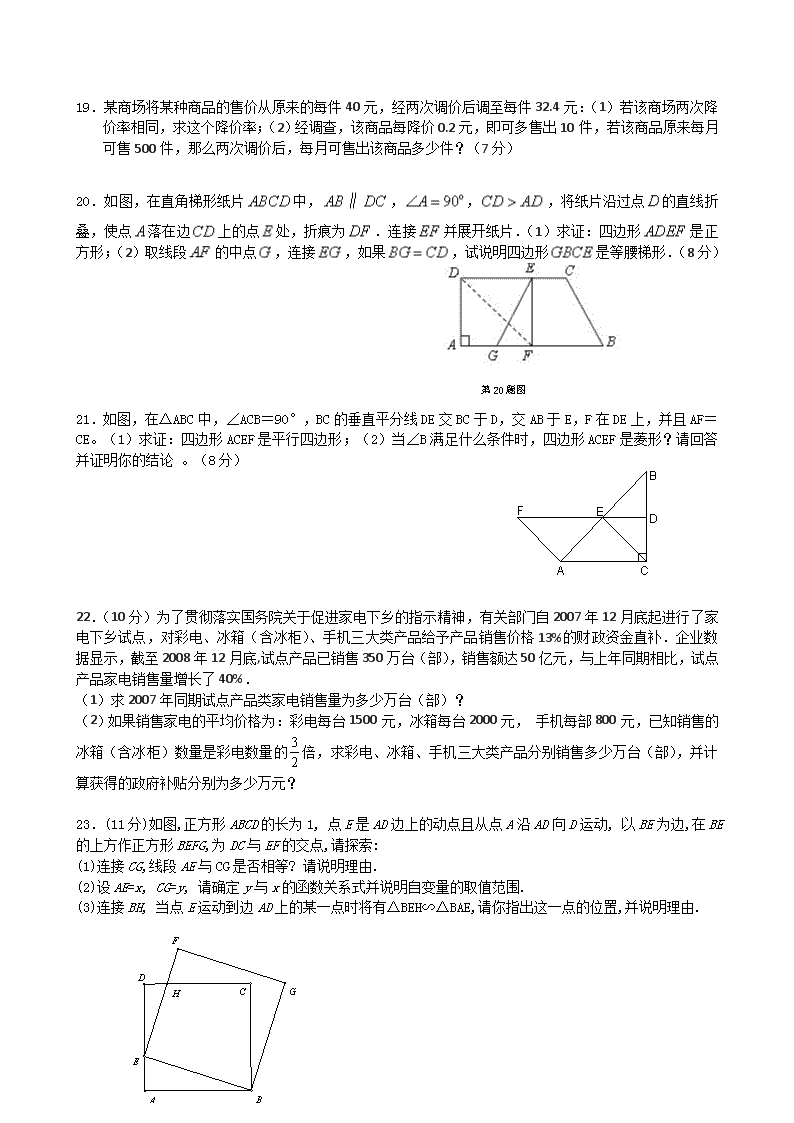
10、如图∠AOP=∠BOP=15°,PC∥OA 交 OB 于 C,PD⊥OA 垂足为 D,若 PC=4,则 PD=( )
A.4 B.3 C.2 D.1
11.如图,在正方形 ABCD 中,E 为 DC 边上的点,连接 BE,将ΔBCE 绕点 C 顺时针方向旋转 90°得到ΔDCF,
连接 EF,若∠BEC=60°,则∠ EFD 的度数为( )A.10° B.15° C.20° D.25°
12.如图,在 Rt⊿ABC 中,∠C=90°, ∠B=22.5°, DE 垂直平分 AB 交 BC 于 E, 若 BE= 2 2 , 则 AC=( )
A.1 B.2 C.3 D.4
13.设 a 和 b 是方程 2 2009 0x x 的两个实数根,则 2 2a a b 的值为( )
A.2006 B.2007 C. 2008 D.2009
14.如图,在等腰梯形 ABCD 中,AB∥CD,AD=BC=acm,∠A=60°,BD 平分∠ABC,则这个梯形的周长是( )
A.4a cm B.5a cm C.6a cm D.7a cm
15.小红按某种规律写出 4 个方程:① 2 2 0x x ;② 2 2 3 0x x ;③ 2 3 4 0x x ;④ 2 4 5 0x x .
按此规律,第五个方程的两个根为( )
A.-2、3 B.2、-3 C.-2、-3 D.2、3
二、解答题(本大题共 9 小题,共 75 分)
16.(6 分)画右边几何体的三种视图(注意符合三视图原则)
17、(6 分)已知,AB 和 DE 是直立在地面上的两根立柱,AB=5m,某一时刻 AB 在阳光下的投影 BC=3m。
(1)请你在图中画出此时 DE 在阳光下的投影;(2)在测量 AB 的投影时,同时测量出 DE 在阳光下的投影
长为 6m,请你计算 DE 的长。
18.(7 分)已知:关于 x 的方程 2 22( 1) 0x m x m (1)当 m 取什么值时,原方程没有实数根;
(2)对 m 选取一个你喜欢的非零整数....,使原方程有两个实数根,并求这两个实数根的平方和。
O D A
B
C P
A B
CD
A
E
D
CB
19.某商场将某种商品的售价从原来的每件 40 元,经两次调价后调至每件 32.4 元:(1)若该商场两次降
价率相同,求这个降价率;(2)经调查,该商品每降价 0.2 元,即可多售出 10 件,若该商品原来每月
可售 500 件,那么两次调价后,每月可售出该商品多少件?(7 分)
20.如图,在直角梯形纸片 中, , , ,将纸片沿过点 的直线折
叠,使点 落在边 上的点 处,折痕为 .连接 并展开纸片.(1)求证:四边形 是正
方形;(2)取线段 的中点 ,连接 ,如果 ,试说明四边形 是等腰梯形.(8 分)
21.如图,在△ABC 中,∠ACB=90°,BC 的垂直平分线 DE 交 BC 于 D,交 AB 于 E,F 在 DE 上,并且 AF=
CE。(1)求证:四边形 ACEF 是平行四边形;(2)当∠B 满足什么条件时,四边形 ACEF 是菱形?请回答
并证明你的结论 。(8 分)
22.(10 分)为了贯彻落实国务院关于促进家电下乡的指示精神,有关部门自 2007 年 12 月底起进行了家
电下乡试点,对彩电、冰箱(含冰柜)、手机三大类产品给予产品销售价格 13%的财政资金直补.企业数
据显示,截至 2008 年 12 月底,试点产品已销售 350 万台(部),销售额达 50 亿元,与上年同期相比,试点
产品家电销售量增长了 40%.
(1)求 2007 年同期试点产品类家电销售量为多少万台(部)?
(2)如果销售家电的平均价格为:彩电每台 1500 元,冰箱每台 2000 元,手机每部 800 元,已知销售的
冰箱(含冰柜)数量是彩电数量的
2
3 倍,求彩电、冰箱、手机三大类产品分别销售多少万台(部),并计
算获得的政府补贴分别为多少万元?
23.(11 分)如图,正方形 ABCD 的长为 1, 点 E 是 AD 边上的动点且从点 A 沿 AD 向 D 运动, 以 BE 为边,在 BE
的上方作正方形 BEFG,为 DC 与 EF 的交点,请探索:
(1)连接 CG,线段 AE 与 CG 是否相等? 请说明理由.
(2)设 AE=x, CG=y, 请确定 y 与 x 的函数关系式并说明自变量的取值范围.
(3)连接 BH, 当点 E 运动到边 AD 上的某一点时将有△BEH∽△BAE,请你指出这一点的位置,并说明理由.
第 20 题图
�
H
�
G
�
E
�
B
�
C
�
A
�
D
�
F
24.(12 分)如图 1,在 2, 90ABC AC AB A 中, ,将一块与 ABC 全等的三角板的直角顶点放在
点 C 上,一直角边与 BC 重叠。
(1)操作 1:固定 ABC ,将三角板沿C B 方向平移,使其直角顶点落在 BC 的中点 M,如图 2 所示,
探究:三角板沿 C B 方向平移的距离为___________;
(2)操作 2:在(1)的情况下,将三角板 BC 的中点 M 顺时针方向旋转角度 (0 90 ) ,如图 3 所示,
探究:设三角形板两直角边分别与 AB、AC 交于点 P、Q,观察四边形 MPAQ 形状的变化,问:四边形 MPAQ
的面积 S 是否改变,若不变,求其面积;若改变,试说明理由;
(3)在(2)的情形下,连 PQ,设 ,BP x MPQ 记 的面积为 y,试求 y 关于 x 的函数关系式,并求 x 为
何值时,y 的值是四边形 MPAQ 的面积的一半,此时,指出四边形 MPAQ 的形状。
期中考试九年级数学参考答案
一、 选择题
1、B 2、A 3、B 4、B 5、B 6、C 7、B 8、D 9、C
10、B 11、B 12、B 13、C 14、B 15、C
二、解答题
16、略
17、(1)略 (2)10m
18、(1)m<-12 (2)、略
19、(1)、10% (2)、880 件
20、(1)、利用“一组邻边相等的矩形是正方形”证明
(2)、过点 C 作 CH⊥AB,证△EFG≌△CHB 得 EG=CB
21、(1)、略 (2)、∠B=30°时,四边形 ACEF 时菱形
22、(1)、250 万台(2 分)
(2)、彩电:88 万台;冰箱:132 万台;手机:130 万部(4 分)
C
A B
M
A B
C
A B
C
M
Q
P
彩电补贴:17160 万元;冰箱补贴:34320 万元;
手机补贴:13520 万元(4 分)
23、(1)、AE=CG 证△ABE≌△CBG(3 分)
(2)、Y=X 0≤ X≤1(3 分)
(3)、当 AE=12 时,△BEH∽△BAE(5 分)
24、(1) 2 ……………………………………………………2 分
(2)不变,连 AM,证 MAQ MBP …………………4 分
AMB ABCMPAQ
1S =S = S =12 四边形
………………………6 分
(3)
1 (2 )2y x x
…………………………………………8 分
由
1 1(2 ) 12 2x x
,解得 1x ………………………10 分
四边形 MPAQ 为正方形………………………………12 分
九年级上数学期中试卷附参考答案
(时间:120 分钟 满分:120 分)
一、选择题(共 12 小题,每小题 3 分,共 36 分.在每小题给出的四个选项中只有一项是符合要求的,请.
将答案填在下面的答题栏内............).
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案
1.下列图形中,既是轴对称图形,又是中心对称图形的个数是( )
A.1 个 B.2 个 C.3 个 D.4 个
2.已知四边形 ABCD ,有以下四个条件:① AB ∥CD ;② CDAB ;③ BC ∥ AD ;④ ADBC .从
这四个条件中任选两个,能使四边形 ABCD 成为平行四边形的选法共有( )
A.6 种 B.5种 C.4 种 D.3 种
3.下列说法中,错误的是( )
A.平行四边形的对角线互相平分 B.矩形的对角线互相垂直
C.菱形的对角线互相垂直平分 D.等腰梯形的对角线相等
4.下列四边形中,两条对角线一定不相等的是( )
A.正方形 B.矩形 C.等腰梯形 D.直角梯形
5.下列说法中:①位似图形一定是相似图形;②相似图形一定是位似图形;③两个位似图形若全等,则位
似中心在两个图形之间;④若五边形 ABCDE 与五边形 A'B'C'D'E'位似,则在五边形中连线组成的△ABC 与
△A'B'C'也是位似的。正确的个数是( )
A.1 B.2 C.3 D.4
6.如图,小区的一角有一块形状为等腰梯形的空地,为了美化小区,社区居委会计划在空地上建一个四
边形的水池,使水池的四个顶点恰好在梯形各边的中点 上,则水池的形状
一定是( )
A.等腰梯形
B.矩形
C.菱形
D.正方形
第 6 题图 第 7 题图 第 8 题图
7.如图,四边形 ABCD 的对角线互相平分,若要使它成为矩形,需要添加的条件是( )
A. CDAB B. BCAD C. BCAB D. BDAC
8.如图,在方格纸上 DEF 是由 ABC 绕定点 P 顺时针旋转得到的.如果用(2,1)表示方格纸上 A 点
的位置,(1,2)表示 B 点的位置,那么点 P 的位置为( )
A.(5,2) B.(2,5) C.(2,1) D.(1,2)
9.如图,在□ABCD 中, E 是 BC 的中点,且 AEC DCE ,则下列结论不正确...的是( )
A.两三角形面积 BEFADF SS 2 B. 1
2BF DF
C.四边形 AECD 是等腰梯形 D. AEB ADC
10.如上图,在平
面 直角坐标系中,将
线 段 OC 向 右 平 移 到
AB,且 OA=O C,形成
菱 形 OABC 的 顶 点
C 的坐标是(3,4),则顶点 A 、 B 的坐标分别是( )
A.(4,0) (7,4) B.(4,0) (8,4)
C.(5,0) (7,4) D.(5,0) (8,4)
11.如上图,在一块形状为直角梯形的草坪中,修建了一条由 A → M → N →C 的小路( M 、 N 分别是
AB 、CD 中点).极少数同学为了走“捷径”,沿线段 AC 行走,破坏了草坪,实际上他们仅少走了( )
A.7 米 B.6 米 C.5 米 D.4 米
12.如右图,两个三角形是位似图形,它们的位似中心 是( )
A.点 P B.点 O C.点 M D.点 N
二、填空题(共 6 小题,每小题 3 分,共 18 分.).
�
E
�
D
�
C
�
B
�
A
13.如图所示,平行四边形 ABCD 的周长是 18cm,AB < AD .对角线 AC 、BD 相交于点O ,若 AOD 与
AOB 的周长差是 5cm,则边 AB 的长是________ cm.
�
O
�
D
�
C
�
B
�
A
第 13 题图
14.如图所示,在等腰梯形 ABCD 中, AD ∥ BC , 60B , 4AD , 7BC ,则梯形 ABCD 的
周长是_____________.
15. 将点 A (3,l)绕原点 O 按顺时针方向旋转 90°到点 B,则点 B 的坐标是 .
16.若两个位似图形中,对应点到位似中心的线段比为 2 :3,则这两个图形对应边的比是
17.将点 P(2,5)沿 X 轴正方向平移 3 个单位,再沿 Y 轴负方向平移 4 个单位后的坐标是
18.如图所示, OAB 绕点O 逆时针
旋转 80 得到 OCD ,若 110A ,
40D ,则 的度数为_________.
三、解答题(本大题共 8 题,共 66 分).
19.(8 分)已知:如图, E 、 F 是□ ABCD 的 对 角 线 AC 上 的 两
点, CFAE .
求证:(1) CBEADF ;(2) EB ∥ DF .
�
F
�
E
�
D
�
C
�
B
�
A
第 19 题图
20.(8 分)如图,在 ABC 中, ACAB , D 为 BC 中点,四边形 ABDE 是平行四边形.求证:四边
形 ADCE 是矩形.
第 20 题图
�
H
�
G
�
F
�
E
�
D
�
C
�
B
�
A
21.(8 分)在梯形 ABCD 中, AD ∥ BC , CDAB , E 为 AD 中点.
(1)求证: ABE ≌ DCE .(2)若 BE 平分 ABC ,且 10AD ,求 AB 的长.
�
E
�
D
�
C
�
B
�
A
第 21 题图
22.(8 分)如图,在四边形 ABCD 中,E、F、G、H 分别是 AB 、 BC 、CD 、 DA 的中点.[来源:学*科
*网 Z*X*X*K]
(1)请判断四边形 EFGH 的形状.并说明为什么?
(2)若使四边形 EFGH 为正方形,那么四边形 ABCD 的对角线应具有怎样的性质?
第 22 题图
[来源:学科网 ZXXK]
[来源:学科网]
23.(12 分)如图,在 ABC 和 CDE 中, CEACAB , DEDCBC ,
AB > BC , DCEBAC ,点 B 、C 、 D 在直线l 上,
(1)按下列要求画图(保留画图痕迹):
①画出点 E 关于直线l 的对称点 E ,连接 EC 、 ED ;
②以点 C 为旋转中心,将(1)中所得 ECD 按逆时针方向旋转,使得 EC 旋转后
的线段C 与CA 重合,得到 EDC (A),画出 EDC .
(2)解决下面问题:
①线段 AB 和线段 DC 的位置关系是 .并说明理由.
②求∠ 的度数.
[来源:Zxxk.Com]
24.(10 分)如图,正方形 ABCD 绕点 A 逆时针旋转 no 后得到正方形 AEFG,EF 与 CD 交于点 O.
(1)以图中已标有字母的点为端点连结两条线段(正方形的对角线除外),要求所连结的两条线段相交且
互相垂直,并说明这两条线段互相垂直的理由;
(2)若正方形的边长为 2cm,重叠部分(四边形 AEOD)的面积为 4 3
3 cm2,求旋转的角度 n.
[来源:学科网 ZXXK]
[来源:学科网]
25.(12 分)已知:如图,在正方形 ABCD 中,点 E 、 F 分别在 BC 和CD 上, AFAE .
(1)求证: DFBE ;
(2)连接 AC 交 EF 于点O ,延长OC 至点 M ,使 OAOM ,连接 EM 、 FM ,判断四边形 AEMF
是什么特殊四边形?并证明你的结论.�
M
�
O
�
F
�
E
�
D
�
C
�
B
�
A
第 25 题图
九年级数学期中质量检测参考答案
一、选择题
题
号 1 2 3[来
源:Zxxk.Com] 4 5 6 7 8 9
10[来
源:学
科网]
11 12
答
案 B C B D C C D A A D B A
二、填空题
13、2; 14、17; 15、(1, 3); 16、2:3; 17、(5,1); 18、 50 .
三、解答题
19、证明:(1)在平行四边形 ABCD 中, AD ∥ BC ,∴ BCEDAC …(2 分)
又∵ CFAE ,∴ EFCFEFAE ,即 CEAF ………………………(4 分)
在 ADF 与 CBE 中,
CEAF
BCEDAC
BCAD
, ∴ CBEADF .…………………………………(6 分)
(2)∵ CBEADF ,∴ CEBAFD ,∴ EB ∥ DF ………………(8 分)
20、证明:∵四边形 ABDE 是平行四边形,∴ AE ∥ BC , DEAB , BDAE .
∵ D 为 BC 的中点,∴ BDCD .[来源:学|科|网]
∵CD ∥ AE , AECD .∴四边形 ADCE 是平行四边形.…………………(7 分)
∵ ACAB ,∴ DEAC ,
∴平行四边形 ADCE 是矩形.(方法不唯一)……………………………………(8 分)
21、证明:(1)∵ AD ∥ BC , CDAB ,∴梯形 ABCD 为等腰梯形,∴ DA .
又∵ E 为 AD 中点,∴ DEAE .
在 ABE 与 DCE 中,
DCAB
DA
DEAE
, ∴ DCEABE …………(4 分)
(2)∵ AD ∥ BC ,∴ EBCAEB .
又∵ BE 平分 ABC ,∴ ABEEBC ,
∴ ABEAEB ,∴ AEAB .
又∵ E 为 AD 中点, 10AD ,
∴ 5 AEAB .………………………………(8 分)
22、(1)四边形 EFGH 是平行四边形.……………………………………(1 分)
连接 AC ,如图所示.………………………………………………………(2 分)
∵ E 、 F 分别是 AB 、 BC 的中点,∴ EF ∥ AC , ACEF 2
1 .
同理 HG ∥ AC , ACHG 2
1 .∴ EF ∥ HG , EF = HG .
∴四边形 EFGH 是平行四边形.…………………………………………………(6 分)
(2)四边形 ABCD 的对角线垂直相等.……………………(8 分;垂直、相等各 1 分)
23、(1)①如图 1 所示………(2 分)②如图 2 所示………(6 分)
(2)①平行.理由:∵ CADEDCDCE ,
∴ CADBAC ,∴ AB ∥ DC ………………………………………(9 分)
②∵ DECD ,∴ DCEDEC .[来源:Z+xx+k.Com]
根据作图可知: CDEADC ,∴ DEDA , DECACD .
又∵ DEBC ,∴ BCDA .由①知 AB ∥ DC ,∴四边形 DABC 是等腰梯形.
又∵ BAC ,∴ 22 BACABDABC .
在 ABC 中,∵ ACAB ,∴ 2ACBABC ,
∴ 18022 ,∴ 36 ……………………………………(12 分)
24(1)连 OA、DE,由 ABCD 是正方形知 AD=AE,所以 Rt△ADO≌Rt△AEO,OD=OE,所以 OA 垂直平分
DE………………………………………………………(6 分)
(2)由(1)知 Rt△ADO≌Rt△AEO,重叠部分面积 S=2S△ADO=2 OD= 4 3
3 ,
所以 OD= 2 3
3
, OD
AD = 3
3
,∠OAD=30°.
所以旋转角 n=∠BAE=90°-2∠OAD=90°-60°=30°……………………………(10 分)
25、(1)证明:∵四边形 ABCD 是正方形,∴ ADAB , 90DB .
∵ AFAE ,∴Rt ABE Rt ADF .∴ DFBE .………………………(5分)
(2)四边形 AEMF 是菱形.…………………………………………………………(7 分)
∵四边形 ABCD 是正方形,∴ 45DCABCA , DCBC .
∵ DFBE ,∴ DFDCBEBC ,即 CFCE .∴ OFOE ………(10 分)
∵ OAOM ,∴四边形 AEMF 是平行四边形.………………………………(11 分)
∵ AFAE ,∴平行四边形 AEMF 是菱形.……………………………………(12 分)
九年级上数学期中考试卷附参考答案 姓名
一.填空题(每题 4 分,共 40 分)
1.三角形的三条 交于一点,这点到三角形各边的距离相等;
2.方程 26)7)(5( xx ,化成一般形式是 ,其二次项的系数和一次项系数的和
是 ;
3.命题:“对顶角相等”的逆命题是 ,它是一个 命题。(填“真”“假”);
4.等腰直角三角形的两边长为 2 cm 和 7 cm ,则它的周长为 ;
5.在横线上填适当的数,使等式成立 22 _____)(_____6 xxx ;
6.如果方程 03)1(2 xkx 的一个根是 1,那么 k 的值是 ,另一个根是 ;
7.一张桌子摆放若干碟子,从三个
方向上看,三种视图如下图所示,
则这张桌子上共有 个碟子;
8.在平行四边形 ABCD 中,对角线 AC 长为 10 cm ,∠CAB=30°,
AB= 6 cm ,则平行四边形 ABCD 的面积为___________ 2cm ;
9.等腰梯形的上、下底分别为 6 cm 、8 cm ,且有一个角为 60°,则它的腰为___________ cm ;
俯视图
主视图
左视图
10.等腰直角三角形斜边上的中线长为 4 cm ,则其面积为 __________;
二.选择题(每小题 3 分,共 24 分)
11.到三角形各顶点的距离相等的点是三角形 ( )
(A) 三边的垂直平分线的交点 (B) 三条高的交点
(C) 三条角平分线的交点 (D) 三条中线的交点
12.顺次连接四边形各边中点所得四边形一定是 ( )
(A)平行四边形 (B)矩形 (C) 菱形 (D)正方形
13.两条对角线垂直且相等的四边形是 ( )
(A)矩形 (B)菱形 (C)正方形 (D) 以上答案均不正确
14.下列命题中,不正确的是 ( )
(A)顺次连结菱形各边中点所得的四边形是矩形 (B)有一个角是直角的菱形是正方形
(C)对角线相等且垂直的四边形是正方形(D)有一个角是 60°的等腰三角形是等边三角形
15.下列方程中,为一元二次方程的是 ( )
(A) 32 yx (B) 312
2
x
(C) 113 22 xxx (D) 02 x
16.小明从正面观察下图所示的两个物体,看到的是 ( )
正面
A B C D
17.如图 5,在宽为 20m,长为 30m 的矩形地面上修建两条同样宽的道路,余下部分作为耕地. 根据图中
数据,计算耕地的面积为
(A) 600m2 (B) 551m2
(C) 550 m 2 (D) 500m2
18.一元二次方程 04
12 xx 的根的情况是 ( )
(A)有两个相等的实数根 (B)有两个不相等的实数根 (C) 无实数根(D)不能确定
三.用指定的方法解方程:(每题 5 分,共 20 分)
(19) 022 xx (因式分解法) (20) 0322 xx (用配方法)
(21) 0892 2 xx (用公式法) (22) 22 )32()2( xx (用合适的方法)
图 5
1m
1m
30m
20m
四.解答题:
23.(6 分)某商场销售一批名牌衬衫,平均每天可售出 20 件,每件盈利 44 元,为了扩大销售,增加盈利,
尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价 1 元,商场平均每天可
多售出 5 件。若商场平均每天要盈利 1600 元,每件衬衫应降价多少元?
24.(6 分)已知关于 x 的方程 03)12( 22 kxkx 有实数根,求 k 的取值范围;
25.(6 分)如图是一个物体的三视图,请画出物体的形状。
26.(7 分)已知:如图平行四边形 ABCD 的对角线 AC 的垂直平分线交 AD 于 E,交 BC 于 F ,求证:四边
形 AFCE 是菱形;
C
D
F
EA
B
俯视图左视图主视图
27.(11 分)已知:如图,在⊿ABC 中,AB=AC,AD BC,垂足为 D,AN 是△ABC 外角 CAM 的平分线,
CE AN,垂足为 E,连接 DE 交 AC 于 F。
(1)求证:四边形 ADCE 为矩形;(4 分)
(2)求证:DF∥AB,DF= 1
2 AB;(4 分)
(3)当⊿ABC 满足什么条件时,四边形 ADCE 是一个正方形?简述你的理由。(3 分)
九年级上数学期中考试卷参考答案
一.
1.内角平分线; 2. 0922 xx , 1 ; 3.相等的角是对顶角,假;
4. cm16 ; 5.9 ,3 ; 6.3 , 32 x ; 7.12个; 8. 215cm ; 9. 2 ; 10. 216cm ;
二.
11.A; 12.A; 13.D; 14.C; 15.D; 16.C; 17.B; 18.B;
三.
CD
F
E N
M
A
PB
19.(1) 01 x , 22 x ;(2) 31 x , 12 x ;(3)
4
179
1
x ,
4
179
2
x ;
(4)
3
1
1 x , 52 x ;
20.解:设每件衬衫应降价 x 元,则有
4,36
014440
160052044
21
2
xx
xx
xx
答:若商场平均每天要盈利 1600 元,每件衬衫应降 36 元或 4 元。但为了尽快减少库存,所以每件衬衫应
降 36 元;
21. 0134124144)3(4)12( 2222 kkkkkk ;
∴
4
13k
22.解:
23.证明:分析:可证四边相等的四边形是菱形;可证一组邻边相等的平行四边形是菱形。
注意:条件是 EF 垂直平分 AC,不是 AC 垂直平分 EF,学生常犯错于此。证明过程略;
24.(1)由 CE⊥AN 得一个直角,由∠MAC 和∠BAC 的角平分线互相垂直得另一个直角,再证 AN∥BP 后
同旁内角互补得第三个直角,有三个角是直角的四边形是矩形;另证合理也给分;(2)由矩形对角线互相
平分得 F 为 AC 的中点,由 AD⊥BC,⊿ABC 是等腰三角形,得 D 为 BC 的中点,可知 ED 是⊿CAB 的中位线,
三角形的中位线平行于第三边且等于第三边的一半;(3)⊿ABC 是等腰直角三角形时满足条件。证明略;
九上册期中复习测试题附参考答案
一、填空题(每题 3 分,共 30 分)
1.如图 1,在△ABC 中,AB=AC,DE 是 AB 的中垂线,△BCE 的周长为 24,BC=10,则 AB=_________.
图 1
2.在△ABC 与△DEF 中,已知∠A=44°15′,∠B=67°12′,∠F=68°33′,∠D=44°15′,且 AC=DF,
那么这两个三角形关系是_________全等.(填“一定”“不一定”“一定不”)
3.如图 2,将面积为 a2 的小正方形与面积为 b2 的大正方形放在一起(b>a>0),则△ABC 的面积为
_________.
图 2
4.在双曲线 y=
x
k 上有一点 P(a,b),且 a,b 是方程 t2-5t+4=0 的两个根,则 k=_________.
5.如果反比例函数 y=(m-3)x 762 mm 的图象在第一、三象限,那么 m=_________.
6.在双曲线 y=
x
k 上有一点 P(a,b),且 a,b 是方程 t2-5t+4=0 的两个根,则 k=_________.
7.点 A(a,b),B(a-1,c)均在函数 y=
x
1 的图象上,若 a<0,则 b_________c(填“>”“<”或“=”
=.
8.已知样本数据 25,21,23,25,27,25,28,30,29,26,24,25,27,22,24,25,26,28,
在列频率分布表时,如果取组距为 2,那么应分成_________组,26.5~28.5 这一组的频率是_________.
9.在样本的频率分布直方图中有 5 个小长方形,已知中间一个长方形面积是其余 4 个长方形面积之
和的
3
1 ,且中间一组频数为 10,则样本容量为_________.
10.口袋中有 3 个黄球,2 个白球,从中任取一个球,用实验的方法估计摸到黄球的概率为_________.
二、选择题(每题 3 分,共 24 分)新 课标 第一网 x kb 1.com
11.下列关于等腰三角形的说法不正确的是( )
A.等腰三角形两腰上的中线相等
B.等腰三角形两腰上的高相等
C.等腰三角形两底角的平分线相等
D.等腰三角形的角平分线、高、中线互相重合
12.已知 x=1 是二次方程(m2-1)x2-mx+m2=0 的一个根,那么 m 的值是( )
A.
2
1 或-1 B.-
2
1 或 1
C.
2
1 或 1 D.
2
1
13.下列方程中,关于 x 的一元二次方程有( )
①x2=0 ②ax2+bx+c=0 ③ 2 x2-3= 5 x ④a2+a-x=0 ⑤(m-1)x2+4x+
2
m =0 ⑥ 2
1
x +
x
1 =
3
1 ⑦
12 x =2 ⑧(x+1)2=x2-9
A.2 个 B.3 个 C.4 个 D.5 个
14.如图 3,D、E 是等边△ABC 的 BC 边和 AC 边上的点,BD=CE,AD 与 BE 相交于 P 点,则∠APE 的
度数是( )
图 3
A.45° B.55° C.60° D.75°
15.到△ABC 的三个顶点距离相等的点是△ABC 的( )
A.三条中线的交点 B.三条角平分线的交点
C.三条高的交点 D.三边垂直平分线的交点
16.统计某校初三年级期中考试数学成绩的频率分布直方图如图 4,从该图可以画出这次考试,数学
成绩的及格率,等于(学习分数都取整数,60 分以下为不及格)( )
图 4
A.0.28 B.0.92 C.0.4 D.1
17.在数学选择题给出的 4 个答案中,只有 1 个是正确的,某同学做 1 道数学选择题,随意地选定其
中的正确答案,答对的概率为( )
A.
4
1 B.
2
1 C.
4
3 D.1
18.一个箱子内有 9 张票,其号数分别为 1,2,……,9,从中任取 1 张,其号数为奇数的概率是
( )
A.
9
2 B.
9
2 C.
9
5 D.
9
7
三、解答题(共 54 分)
19.(4 分)画出图 5 中树的影子.
图 5
20.(10 分)如图 6,△ABC 中,AD⊥BC 于 D 点,E、F 分别是 AB、AC 的中点.
图 6
(1)EF 与 AD 间有什么特殊的位置关系?请证明你的结论.
(2)若四边形 AEDF 是菱形,问△ABC 应满足什么条件、为什么?
21.(10 分)已知:双曲线 y=
x
a8 与直线 y=ax+2 的一个交点的横坐标是 4.
求:(1)两个函数的解析式;
(2)另一交点的坐标.
22.(10 分)某工厂 1998 年初投资 100 万元生产某种新产品,1998 年底将获得的利润与年初的投资
的和作为 1999 年初的投资,到 1999 年底,两年共获利润 56 万元,已知 1999 年的年获利率比 1998 年的
年获利率多 10 个百分点,求 1998 年和 1999 年的年获利率各是多少?
23.(10 分)请同学们认真阅读下面的一段文字材料,然后解答题目中提出的有关问题.
为解方程(x2-1)2-5(x2-1)+4=0,我们可以将 x2-1 视为一个整体,然后设 x2-1=y,则原方程
可化为 y2-5y+4=0 ①
解得 y1=1,y2=4
当 y=1 时,x2-1=1,∴x2=2,x=± 2
当 y=4 时,x2-1=4,∴x2=5,x=± 5
∴原方程的解为 x1= 2 ,x2=- 2 ,x3= 5 ,x4=- 5
解答问题:
(1)填空:在由原方程得到方程①的过程中,利用_________法达到了降次的目的,体现了_________
的数学思想.
(2)解方程 x4-x2-6=0
24.(10 分)如图 7,A、B、C、D 为矩形的四个顶点,AB=16cm,AD=6cm,动点 P、Q 分别从点 A、C
同时出发,点 P 以 3cm/s 的速度向点 B 移动,一直到达 B 为止,点 Q 以 2cm/s 的速度向 D 移动.
图 7
(1)P、Q 两点从出发开始到几秒时四边形 PBCQ 的面积为 33cm2?
(2)P、Q 两点从出发开始到几秒时,点 P 和点 Q 的距离是 10cm?
四、综合探究题(12 分)
25.(12 分)图形 8 的操作过程(本题中四个矩形的水平方向的边长均为 a,坚直方向的边长均为 b):
在图(1)中,将线段 A1A2 向右平移 1 个单位到 B1B2,得到封闭图形 A1A2B2B1(即阴影部分);
在图(2)中,将折线 A1A2A3 向右平移 1 个单位到 B1B2B3,得到封闭图形 A1A2A3B3B2B1(即阴影部分).
(1)在图(3)中,请你类似地画一条有两个折点的折线,同样向右平移 1 个单位,从而得到一个封
闭图形,并用斜线画出阴影;
(2)请你分别写出上述三个图形中除去有影部分后剩余的面积:
S1=_________,S2=_________,S3=_________;
(3)联想与探索
如图 9,在一块矩形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是 1 个单位),请你
猜想空白部分的草地面积是多少?并说明你的猜想是正确的.
图 9
新 课标 第 一网 x kb 1.com
参考答案
一、1.36(提示:连接 AC,可得 AC=5,再根据勾股定理的逆定理,由 52+122=132 可知△ACD 是直角三角
形,则四边形 ABCD 的面积就是△ABC 和△ACD 的面积和)2.14 3.36° 4.
2
1 b2(提示:小、大正方形
的边长分别是 a、b,由图形易知:△ABC 的面积=梯形 AEGB 的面积+△AGC 的面积—△AEC 的面积) 5.4(提
示:令 m2-6m+7=-1 且 m-3>0 解得 m=4) 6.4(提示:解得 a、b 的值分别为 1、4 或 4、1,然后将 p
(1,4)或(4,1)代入 y=
x
k 得:k=4) 7.< 8.5 0.22 9.40 10.
5
3
二、11. D(提示:注意命题表达的严谨性,正确叙述为:等腰三角形的顶角的平分线、底边上的高线、
中线互相重合) 12.D(提示:因是二次方程,故 m2-1≠0,勿错选 B) 13. A (提示:由定义可知,一
元二次方程需满足三个条件 1.整式方程 2.只含有一个未知数 3.最高次数 1,三者缺一不可,易知①③是一
元二次方程) 14.C(提示:证明△ABD≌ △BCE 即可) 15. D 16.B 17.A 18.C
三、19.略 20.(1)互相垂直 证明(略) (2)AB=AC 证明(略)
21.(1)y=-
x
8 y=-x+2 (2)(-2,4)
22.设 98 年的年利率为 x,则 99 年的为 x+10%
100x+(100+100x)(x+10%)=56
x1=20%,x2=-2.3(舍)
∴x+10%=30%
23.(1)换元 转化 (2)x1= 3 ,x2=- 3
24.(1)5 秒 (2)
5
8 秒
四、25.新课 标第一 网 xk b1.com
解:(1)画图(要求对应点在水平位置上,宽度保持一致)
(2)ab-b ab-b ab-b.
(3)猜想:依据前面的有关计算,可以猜想草地的面积仍然是 ab-b.
方案:1.将“小路”沿着左右两个边界“剪去”;
2.将左侧的草地向右平移一个单位;
3.得到一个新的矩形(如上图)。
理由:在新得到的矩形中,其纵向宽仍然是 b,
其水平方向的长变成了 a-1,
所以草地的面积就是:b(a-1)=ab-b.
九年级数学第一学期期中考试试卷
一.选择题:(每小题 3 分,共 24 分)
1.在同一时刻的阳光下,小明的影子比小强的影子长,那么在同一路灯下 ( )
A.小明的影子比小强的影子长 B.小明的影子比小强的影子短
C.小明的影子和小强的影子一样长 D.无法判断谁的影子长
2.如图,平行四边形 ABCD 的周长为 cm16 ,AC、BD 相交于点 O,OE⊥AC 交 AD 于 E,则△DCE 的周长
为 ( )
A.4 cm B.6 cm C.8 cm D.10 cm
3.到△ABC 的三边距离相等的点是△ABC 的( )
A.三条中线的交点 B.三条角平分线的交点
C.三条高的交点 D.三条边的垂直平分线的交点
4.如图所示的几何体的俯视图是 ( )
5.根据下列表格的对应值:
x 3.23 3.24 3.25 3.26
cbxax 2 -0.06 -0.02 0.03 0.07
判断方程 02 cbxax ( a ≠0, a ,b , c 为常数)的一个解 x 的范围是 ( )
A.3< x <3.23 B.3.23< x <3.24
C.3.24< x <3.25 D.3.25 < x <3.26
6.等腰三角形的腰长等于 2 m ,面积等于 1 2m ,则它的顶角等于( )
A.150o B.30o C.150o 或 30o D.60o
7.利用 13 米的铁丝和一面墙,围成一个面积为 20 平方米的长方形,墙作为长方形的长
边,求这个长方形的长和宽。设长为 x 米,可得方程 ( )
A. 20)13( xx B. 20)2
13( xx
C. 20)2
113( xx D. 20)2
213( xx
8.如图,小亮拿一张矩形纸图(1),沿虚线对折一次得图(2),下将对角两顶点重合折叠得图(3)。按
图(4)沿折痕中点与重合顶点的连线剪开,得到三个图形,这三个图形分别是( )
A.都是等腰梯形 B.两个直角三角形,一个等腰三角形
C.两个直角三角形,一个等腰梯形 D.都是等边三角形
二.填空题:(每小题 3 分,共 30 分)
9.写出一个一元二次方程,使方程有一个根为 0,并且二次项系数为 1:
10.用反证方法证明“在△ABC 中,AB=AC,则∠B 必为锐角”的第一步是假设
11.如图,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若 PC = 4,则 PD 的长为 ;
12.如图,在△ABC 中,BC cm5 ,BP、CP 分别是∠ABC 和∠ACB 的角平分线,且 PD∥AB,PE∥AC,则
△PDE 的周长是 cm
A
D C
B
E
G
F
13.三角形两边长分别为 3 和 6,如果第三边是方程 2 6 8 0x x 的解,那么这个三角形的周长
14.直角三角形的两条边长分别为 6 和 8,那么这个直角三角形斜边上的中线长等于
15.矩形纸片 ABCD 中, AD = 4 cm , AB = 10 cm , 按如图方式折叠, 使点 B 与点 D 重合, 折痕为 EF,则 DE =
cm ;
16.如图,P 是等边三角形 ABC 内一点,将△ABP 绕点 B 顺时针方向旋转 60°,得到△CBP′,若 PB=3,则 PP′=
17.小军同学家开了一个商店,今年 1 月份的利润是 1000 元,3 月份的利润是 1210 元,请你帮助小军同学
算一算,他家的这个商店这两个月的利润平均月增长率是___________
18.如图,菱形 ABCD 的对角线的长分别为 2 和 5,P 是对角线 AC 上任一点(点 P 不与 点 A、C 重合), 且
PE∥BC 交 AB 于 E,PF∥CD 交 AD 于 F,则阴影部分的面积是______;
三.解答题
19. 用适当的方法解下列方程
(1) 12)1)(8( xx (2) )4(5)4( 2 xx
20、已知,如图,AB 和 DE 是直立在地面上的两根立柱.AB=5m,某一时刻
AB 在阳光下的投影 BC=3m.在测量 AB 的投影时,同时测量出 DE 在阳光下
的投影长为 6m,请你做出 DE 的影子并计算 DE 的长.
21. 已知:如图,四边形 ABCD 是菱形,E 是 BD 延长线上一点,F 是 DB 延
长线上一点,且 DE=BF。请你以 F 为一个端点,和图中已标明字母的某一点连成一条新的线段,猜想并证
明它和图中已有的某一条线段相等(只须证明一组线段相等即可) .
(1)连结__AF__________ ;
(2)猜想:___AF___ =_AE_____ ;
(3)证明:
22、已知:如图, E 是正方形 ABCD 的对角线 BD 上一点,EF⊥BC, EG⊥CD,
垂足分别是 F、G . 求证:AE = FG.
23.某超市经销一种成本为 40 元/ kg 的水产品,市场调查发现,按 50 元/ kg 销售,一个月能售出 500 kg ,
若每 kg 每涨 1 元,月销售量就减少 10 kg ,针对这种水产品的销情况,超市在月成本不超过 10000 元的情
况下,使得月销售利润达到 8000 元,请你帮忙算算,销售单价定为多少?
24.如图 4,(1)F 是正方形 ABCD 的边 BC 的中点,CG 平分∠DCM,交过 F 点 AF 的垂线 FG 于 G,
求证:AF=FG.(2)若点 F 是正方形 ABCD 的边 BC 上任意一点,其他条件不变,(1)中结论是
否仍然成立?
图 4
25.如图,点 C 为线段 AB 上一点,△ACM、△CBN 是等边三角形,直线 AN、MC 交于点 E,直线 BM、CN
交于点 F。
(1)求证:AN=MB
(2)求证:△CEF 为等边三角形
(3)将△ACM 绕点 C 按逆时针方向旋转 90°,其他条件不变,在(2)中画出符合要求的图形,并判断(1)
(2)题中的两结论是否依然成立。并说明理由
九年级数学上期中测试题
一、选择题(3 分×10=30 分)
1.下列方程,是一元二次方程的是( )
①3x2+x=20,②2x2-3xy+4=0,③x2-
1
x =4,④x2=0,⑤x2- 3
x
+3=0
A.①② B.①②④⑤ C.①③④ D.①④⑤
2.在抛物线 132 2 xxy 上的点是( )
A.(0,-1) B.
0,2
1 C.(-1,5) D.(3,4)
3.直线 22
5 xy 与抛物线 xxy 2
12 的交点个数是( )
A.0 个 B.1 个 C.2 个 D.互相重合的两个
4.关于抛物线 cbxaxy 2 (a≠0),下面几点结论中,正确的有( )
1 当 a0 时,对称轴左边 y 随 x 的增大而减小,对称轴右边 y 随 x 的增大而增大,当
a0 时,情况相反.
抛物线的最高点或最低点都是指抛物线的顶点.
2 只要解析式的二次项系数的绝对值相同,两条抛物线的形状就相同.
3 一元二次方程 02 cbxax (a≠0)的根,就是抛物线 cbxaxy 2 与 x 轴 交点
的横坐标.
A.①②③④ B.①②③ C. ①② D.①
5.已知点 A 的坐标为(a,b),O 为原点,连结 OA,将线段 OA 绕点 O 按逆时针方向旋转 90°得 OA1,则
点 A1 的坐标为 .
A.(-a,b) B.(a,-b) C.(-b,a) D.(b,-a)
6.方程(x-3)2=(x-3)的根为( )
A.3 B.4 C.4 或 3 D.-4 或 3
7.如果代数式 x2+4x+4 的值是 16,则 x 的值一定是( )
A.-2 B.2 3 ,-2 3 C.2,-6 D.30,-34
8.若 c(c≠0)为关于 x 的一元二次方程 x2+bx+c=0 的根,则 c+b 的值为( )
A.1 B.-1 C.2 D.-2
9.从正方形铁片上截去 2cm 宽的一个长方形,剩余矩形的面积为 80cm2,则原来正方形的
面积为( )
A.100cm2 B.121cm2 C.144cm2 D.169cm2
10.方程 x2+3x-6=0 与 x2-6x+3=0 所有根的乘积等于( )
A.-18 B.18 C.-3 D.3
11.三角形两边长分别是 8 和 6,第三边长是一元二次方程 x2-16x+60=0 一个实数根,则该三
角形的面积是( )
A.24 B.48 C.24 或 8 5 D.8 5
二、填空题(3 分×10=30 分)
12.二次函数 )()(3 2 xy 的图象的顶点坐标是(1,-2).
13.已知 2)1(3
1 2 xy ,当 x 时,函数值随 x 的增大而减小.
14.已知直线 12 xy 与抛物线 kxy 25 交点的横坐标为 2,则 k= ,交点坐
标为 .
15、如图,△ABC 为等腰三角形,AB=AC,∠A=38°,现将△ABC 绕点旋转,使 BC 的对应边落在 AC 上,
则其旋转角为 .
14.用配方法将二次函数 xxy 3
22 化成 khxay 2)( 的形式是 . X k B 1 . c o m
16.x2-10x+________=(x-________)2.
17.若关于 x 的一元二次方程(m+3)x2+5x+m2+2m-3=0 有一个根为 0,则 m=______,另一
根为________.
18.方程 x2-3x-10=0 的两根之比为_______.
19.已知方程 x2-7x+12=0 的两根恰好是 Rt△ABC 的两条边的长,则 Rt△ABC的第三边长为
________.
20.一个两位数,个位数字比十位数字大 3,个位数字的平方刚好等于这个两位数,则这个
两位数是________.
21.某超市从我国西部某城市运进两
种糖果,甲种 a 千克,每千克 x 元,乙
种 b 千克,每千克 y 元,如果把这两种
糖果混合后销售,保本价是_________
元/千克.
22、在直角坐标中,已知点 A(-3,0),
B(0,4),对△OAB 连续作旋转变换,依
次得到三角形①、②、③、④、…,则三角
形⑩的直角顶点坐标为 . X k B
1 . c o m
A. 38° B. 52° C. 71° D. 81°
三、解答题(共 60 分)
23.用适当的方法解下列方程(每小题 3 分,共 12 分)
(1)(3x-1)2=(x+1)2 (2)2x2+x-
1
2 =0
(3)用配方法解方程:x2-4x+1=0;p
(4)用换元法解方程:(x2+x)2+(x2+x)=6X k B 1 . c o m
24.(9)已知方程 2(m+1)x2+4mx+3m=2,根据下列条件之一求 m 的值.
(1)方程有两个相等的实数根;(2)方程有两个相反的实数根;
(3)方程的一个根为 0.
25.(8 分)已知 x1,x2 是一元二次方程 2x2-2x+m+1=0 的两个实数根.
(1)求实数 m 的取值范围;
(2)如果 x1,x2 满足不等式 7+4x1x2>x12+x22,且 m 为整数,求 m 的值.
26、如图,点 O 是边长为 a 的正方形 ABCD 的对称中心,过点作 OM ⊥ ON
交正方形的边于 M、N 两点,求四边形 OMCN 的面积.
27.(8))已知 +3x+6 是二次函数,求 m 的值,并判断此抛物线开口方向,写
出顶点坐标及对称轴。
28. (10分)已知抛物线 y=ax2+bx+c 如图所示,直线 x=-1是其对称轴,(1)确定 a,b,c,
Δ=b2-4ac 的符号,(2)求证:a-b+c>0, (3)当 x 取何值时,y>0, 当 x 取何值时 y<0。
29、将两块含 30°角且大小相同的直角三角板如图⑴摆放,再将图⑴中△A1B1C
绕点 C 顺时针旋转 45°后得图⑵,点 P1 是 A1C 与 AB 的交点.
求证:CP1= AP1.
30.(13 分)已知抛物线 y=x2+ bx+c 与 y 轴交于点 Q(0,-3),图象与 x 轴两交点的横坐标
的平方和为 15,求函数解析式及对称轴。
w W w .x K b 1.c o M
1.D 2.B 3.C 4.A 5.C 6.C 7.B 8.A 9.A 10.C
11.-1,-2; 12.x-1; 13.-17,(2,3); 14.
9
1
3
1 2
xy ;15.25,5 16.1,-
5
4 17.-
5
2
或-
2
5 18.5 或 7 19.25 或 36 20.
ax by
a b
21.(1)x1=0,x2=1;(2)x=-
1
4 ±
5
4 ;
(3)(x-2)2=3,x1=2+ 3 ,x2=2- 3 ;
(4)设 x2+x=y,则 y2+y=6,y1=-3,y2=2,则 x2+x=-3 无解,x2+x=2,x1=-2,x2=1.
22.△=16m2-8(m+1)(3m-2)=-8m2-8m+16,
(1)方程有两个相等的实数根,
∴△=0,即-8m2-8m+16=0,求得 m1=-2,m2=1;
(2)因为方程有两个相等的实数根,X|k | B| 1 . c|O |m
所以两根之和为 0 且△≥0,则-
4
2( 1)
m
m =0,求得 m=0;
(3)∵方程有一根为 0,∴3m-2=0 得 m=
2
3 .
23.(1)△=-8m-4≥0,∴m≤-
1
2 ;(2)m=-2,-1
24.解:由题意得 解得 m=-1
∴y=-3x2+3x+6= ,
开口向下,顶点坐标( ),对称轴 x= 。X k B 1 . c o m
25. 解:(1)由抛物线的开口向下,得 a<0,由抛物线与 y 轴的交点在 x 轴上方,得 c>0,
又由 <0,∴ >0,
∴a、b 同号,由 a<0得 b<0.
由抛物线与 x 轴有两个不同的交点,
∴Δ=b2-4ac>0
(2)由抛物线的顶点在 x 轴上方,对称轴为 x=-1.
∴当 x=-1时,y=a-b+c>0
(3)由图象可知:当-3
0 ,
∴当 x<-3或 x>1时,y<0
26. 解:由点 Q(0,-3)知 c=-3,则抛物线的解析式为
设图象与 x 轴交点的横坐标为 ,
∴ 是二次方程 的两个根,
由根与系数的关系得: 新
∴
解得:
∴所求函数的解析式 ,
对称轴分别为 .
25.解:连结 OD、OC
则 OD⊥OC,=
∵OM⊥ON,∴将△ODM 绕 O 点沿顺时针方向
旋转 90°后,得到△OCN,
因此,△ODM≌△OCN,=
∴= ,即,=.
26.解:由△DEC 按顺时针方向旋转得到△DAG,
则△DEC≌△DAG,
∴∠1=∠2,http://w ww. xkb1 . com
∵∠ADC=90°,∠EDF=45°
∴∠1+∠ADF=45°
即,∠GDF=∠2+∠ADF=∠1+∠ADF=45°.
27.解:过 P1 作 P1M⊥AC 于 M,
则∠P1MC=90°
∵∠P1CM=∠BCA1=45°
∴CP1=P1M,
∵∠A=30°
∴P1M=A1P,即,CP1=A1P.
新课 标九年级上册数学期中试题附参考答案
第Ⅰ卷(选择题,共 30 分)
一、选择题(共 10 小题,每小题 3 分,共计 30 分。每小题只有一个选项是正
确的。请把选项填在答题卡中。)
题号 1 2 3 4 5 6 7 8 9 10
选项
1、矩形、菱形、正方形都具有的性质是( )
A.每一条对角线平分一组对角 B.对角线相等
C.对角线互相平分 D.对角线互相垂直
2、下列关于 的方程:① ;② 1)1()9(3 22 xx ;③
xx 13 ;
④ )1)(1(22 xxxx ;⑤ 012 yx ,其中一元二次方程的个数是( )
A.1 B.2 C.3 D.4
3、若 为方程 的解,则 的值为( )
A.12 B.6 C.9 D.16
4、下列说法正确的是 ( )
①试验条件不会影响某事件出现的频率;
②在相同的条件下试验次数越多,就越有可能得到较精确的估计值,但各人所得的值
不一定相同;
③如果一枚骰子的质量分布均匀,那么抛掷后每个点数出现的机会均等;
④抛掷两枚质量分布均匀的相同的硬币,出现“两个正面”、“两个反面”、“一正一反”的机
会相同.
A.①② B.②③ C.③④ D.①③
5、若关于 x 的一元二次方程 2 21 1 0a x x a 的一个根是 0,则 a 的值是( )
A、 1 B、 -1 C 、 1 或-1 D、 1
2
6、如右图,在△ABC 中,看 DE∥BC, 1
2
AD
BD
,DE=4 cm,则 BC 的长为 ( )
A.8 cm B.12 cm C.11 cm D.10 cm
7、已知 065 22 yxyx ,则 xy : 等于 ( )
A、
2
1
3
1 或 B、 32或 C、 16
1 或 D、 16或
8、根据下列表格对应值:
x 3.24 3.25 3.26
2ax bx c -0.02 0.01 0.03
判断关于 x的方程 2 0( 0)ax bx c a 的一个解 x 的范围是( )
A. x<3.24 B.3.24< x<3.25
C.3.25< x<3.26 D.3.25< x<3.28
9.如图,已知四边形 ABCD 是平行四边形,下列结论中不正确的是( )
A.当 AB=BC 时,它是菱形 B.当 AC⊥BD 时,它是菱形
C.当∠ABC=90°时,它是矩形 D.当 AC=BD 时,它是正方形
10、如图,ABC 中,DE//BC,BE 与 CD 交于点 O,AO 与 DE、BC 交于 N、M,则下列式子中错
误的是( )
A. DN
BM
AD
AB
B. AD
AB
DE
BC
C. DO
OC
DE
BC
D. AE
EC
AO
OM
A
N
O
B M C
D E
(第 10 题图) (第 18 题图)
第Ⅱ卷(非选择题,共 90 分)
二、填空题。(每小题 3 分,共计 24 分,请把答案填在答题卡中。)
题号 11 12 13 14 15 16 17 18
答案
11、已知 a、b、c、d 四条线段依次成比例,其中 a=3cm,b=(x-1)cm,c=5cm,d=(x+1)
cm,则 x= .
12、关于 x 的方程 03)3( 12 xxm m 是一元二次方程,则 m ;.
13、已知矩形的两条对角线的夹角为 1200,一条对角线的长为 2 厘米,则矩形的面积为
_________.
14、已知: ,kz
yx
y
zx
x
zy 则 k 的值是 ;
15、已知: ,3
4
2
x
yx 则
y
x = ;
16、已知菱形的周长为 ,一条对角线长为 ,则这个菱形的面积为_________;
17、某小区 2010 年屋顶绿化面积为 2000 平方米,计划 2012 年屋顶绿化面积要达到 2880
平方米.如果每年屋顶绿化面积的增长率相同,那么这个增长率是 ;
18、如图,正方形 ABCD 的边长为 8,M 在 DC 上,且 DM=2,N 是 AC 上一动点,则 DM+DN 的最
小值为
三、解答题(共 66 分)
19、解方程:(16 分)
① 223 2 xxx ② 05222 2 xx
③ 02)23(3)23( 2 xx ④ 0121)1( 2 x
20、(8 分)某旅游景点为了吸引游客,推出的团体票收费标准如下:如果团体人数不超过 25
人,每张票价 150 元,如果超过 25 人,每增加 1 人,每张票价降低 2 元,但每张票价不得低
于 100 元,阳光旅行社共支付团体票价 4800 元,则阳光旅行社共购买多少张团体票.
21、(8 分)如图,在△ABC 中,∠B=90°,AB=6cm,BC=8cm,若点 P 从点 A 沿 AB 边向
B 点以 1cm/s 的速度移动,点 Q 从 B 点沿 BC 边向点 C 以占 2cm/s 的速度移动,两点同时
出发.
(1)问几秒后,△PBQ 的面积为 8cm2?(2)出发几秒后线段 PQ 的长为 4 cm?
22、(8 分)如图,在矩形 ABCD 中,E 是边 CB 延长线上的点,且 EB=AB,DE 与 AB 相交于点 F,
AD=3,CD=2,求 AE 及 DF 的长.
23、(8分)将分别标有数字1,2,3 的三张卡片洗匀后,背面朝上放在桌上.
(1)随机抽取一张,求抽到奇数的概率;
(2)随机抽取一张作为十位上的数字(不放回),再抽取一张作为个位上的数字,能组成
哪些两位数?恰好是 32 的概率是多少
24、(8 分)关于 x 的一元二次方程 x2-3x-k=0 有两个不相等的实数根
①求k的取值范围
②请选择一个k的负整数值,并求出方程的根
25.(10 分)如图,在平行四边形 ABCD 中,E,F 分别 AB、CD 的中点,BD 是对角线,过 A 作
AG∥DB 交 CB 的延长线于点 G
①求证:DE∥BF
②若∠G=90°,求证:四边形 DEBF 是菱形
参考答案
一、选择题(共 10 小题,每小题 3 分,共计 30 分。每小题只有一个选项是正
确的。)
题号 1 2 3 4 5 6 7 8 9 10
选项 C A B B B B A B D D
二、填空题。(每小题 3 分,共计 24 分)
题号 11 12 13 14 15 16 17 18
答案 4 3 23cm -1 或 2 5
3
96 20% 10
三、解答题(共 66 分)
19、解方程:(16 分)
① 1 22 3x x , .;② 1
2 2 3
2x , 2
2 2 3
2x
;
③ 0,3
1
21 xx ;④ 12,10 21 xx ;
20、(8 分)解:∵150×25=3750<4800,
∴购买的团体票超过 25 张, ------------------------------------1 分
设共购买了 x 张团体票,由题意得:x·[150-2(x-25)]=4800, -----5 分
整理的:x2-100x+2400=0,
解得:x1=60(不符题意,舍去)x2=40,——7 分
答:共购买了 40 张团体票.———————8 分
21、(8 分)解:设 P、Q 经过 t 秒时,△PBQ 的面积为 8cm2,
则 AP=tcm,PB=(6-t)cm,BQ=2tcm,
由题意得: 82)6(2
1 tt
解得,t1=2,t2=4,
∴当 P、Q 经过 2 或 4 秒时,△PBQ 的面积为 8cm 2;————————4 分
(2)设 x 秒后,线段 PQ 的长为 4 cm。
由题意得 2)6( x +(2x)2= 2)24(
解得:x1= 2
5
,x2=2
答: 2
5
或 2 秒后,线段 PQ 的长为 4 cm。—————————8 分
22. (8分)AE= 22 ---------------------------------3分
DF= 295
3 ————————————————8分
23、(8分)(1)P(奇数)= 2
3
.————————————2分
(2)恰好是32的概率是 1
6
. ------------------------8分
24、(8分)①
4
9k -------------------------------------4分
②
2
53
2
530131
21
4
9
21
2
xxxxk
k
kk
,,解得:时,原方程为:当
或
为负整数。,且解:
210232 21
2 xxxxk ,,解得:时,原方程为:当
——————8分
(选择一个值即可)
25、(10分)1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∵点E、F分别是AB、CD的中点
∴BE= 2
1 AB,DF= 2
1 CD.
∴BE=DF,
∵AB∥CD ,即BE∥DF,
∴四边形DFBE是平行四边形,
∴DE∥BF,————————————————————————5分
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,即AD∥BG
∵AG∥BD,
∴四边形AGBD是平行四边形,
∴∠ADB=∠G=90°,
在 Rt △ADB中,∠ADB=90°,E为AB的中点,
∴DE= 2
1 AB,
∵BE=
2
1 AB
∴DE=BE
∴平行四边形DEBF是菱形. ------------------------------------------------ 10分
九 年 级 数 学 期 中 考 试 卷
题 号 一 二 三 总 分
得 分
一、选择题(每题 3 分,共 24 分)
1、已知一元二次方程 x2-6x+c=0 有一个根为 2,则另一个根为( )
A.2 B.3 C.4 D.8
2、如图,矩形 ABCD 的两条对角线相交于点 O,∠AOB=60·AB=2,则矩形的对角线 AC 的长是( )
A.2 B.4 C.2 3 D.4 3 X k B 1 . c o m
3、在一个不透明的口袋中装有 4 个红球和若干个白球,他们除颜色外其他完全相同.通过多次摸球实验
后发现,摸到红球的频率稳定在 25%附近,则口袋中白球可能有( )
A.16 个 B.15 个 C.13 个 D.12 个
4、已知点 C 是 AB 的黄金分割点(AC >BC),若 AB=4cm,则 AC 的长为( )
A.(2 5 –2)cm B. (6-2 5 )cm C. ( 5 –1)cm D. (3- 5 )cm
5、如图,每个小正方形边长均为 1,则下列图中的三角形(阴影部分)与左图中 相似的是( )
A. B. C. D.
A
B C
6、如图,在菱形 ABCD 中,AB=3,∠ABC=60°,则对角线 AC=( )
A.12 B.9 C.6 D.3 X k B 1 . c o m
7、目前我国已建立了比较完善的经济困难学生资助体系,某校去年上半年发放给每个经济困难学生 389
元,今年上半年发放了 438 元.设每半年发放的资助金额的平均增长率为 x,则下面列出的方程中正确的
是( )
A.438(1+x)2=389 B.389(1+x)2=438
C.389(1+2x)=438 D.438(1+2x)=389
8、如图,在对角线长分别为 12 和 16 的菱形 ABCD 中,E,F 分别是边 AB,AD 的中点,H 是对角线 BD 上
的任意一点,则 HE+HF 的最小值是( )
A.14 B.28 C.6 D.10
二、填空题(每题 3 分,共 24 分) 新- 课 -标- 第 -一- 网
9 、 设 一 元 二 次 方 程 x 2 - 7x + 3 = 0 的 两 个 实 数 根 分 别 为 x 1 和 x 2 , 则 x 1 + x 2
= , x 1 ·x 2 = .
10 、 .已知:如图 L1∥L2∥L3,AB=3,DE=2,EF=4,则 BC= .
11 、 如 图 折 叠 一 张 矩 形 纸 片 , 已 知 ∠ 1 = 70 ° , 则 ∠ 2 的 度 数 是 .
12、若
b
a =
d
c =
f
e =3,且 b+d+f=4,则 a+c+e= .
13、如 果 关 于 x 的 一 元 二 次 方 程 有 实 数 根 , 那 么 k 的 取 值 范 围 是
X k B 1 . c o m
14、如图,四边形 ABCD 是正方形,延长 BC 至点 E,使 CE=AC,连接 AE,AE 交 CD 于点 F,那么∠AFC
等于______________________。
15、如图,D 是△ABC 的边 AB 上一点,若∠1=_____________,则△ADC∽△ACB,若∠
2=___________________,则△ADC∽△ACB 新课 标 第 一 网
16、把一张矩形纸片(矩形 ABCD)按如图方式折叠,使顶点 B 和点 D 重合,折痕为 EF.若 AB = 3 cm,BC
= 5 cm,则重叠部分△DEF 的面积是 .cm2.
三 、 解 答 题 ( 17 题 12 分 , 18 题 ~ 21 题 每 题 10 分 )
17 、 选 用 适 当 的 方 法 解 下 列 一 元 二 次 方 程 w W w .x K b 1.c o M
(1) x2 =64 (2) 2(2x-1)-x(1-2x)=0
(3) x 2 + 2x + 3=0 (4)3x 2 +2x-1 =0
18、某商场销售一批名牌衬衫,平均每天可售出 20 件,每件盈利 40 元,为了扩大销售量增加盈利,尽快
减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价 1 元,商场平均每天可多售
2 件,如果商场平均每天要盈利 1200 元,每件衬衫应降价多少元?
新课 标 第 一 网
19、有 四 张 规 格 、 质 地 相 同 的 卡 片 , 它 们 背 面 完 全 相 同 , 正 面 图 案 分 别 是 (A )菱 形 ,
(B)平 行 四 边 形 , ( C) 线 段 , (D )角 , 将 这 四 张 卡 片 背 面 朝 上 洗 匀 后 ,
(1) 随 机 抽 取 一 张 卡 片 图 案 是 轴 对 称 图 形 的 概 率 是 ________ ;
B
CA
QP
(2) 随 机 抽 取 两 张 卡 片 (不 放 回 ), 求 两 张 卡 片 图 案 都 是 中 心 对 称 图 形 的 概 率 , 并 用 树
状 图 或 列 表 法 加 以 说 明 . 新| 课 |标|第 |一| 网
X k B 1 . c o m
20、在∆ABC 中,AB=8cm,BC=16cm,点 P 从点 A 开始沿 AB 边向 B 点以 2cm/秒的速度移动,点 Q 从点 B 开
始沿 BC 向点 C 以 4cm/秒的速度移动,如果 P、Q 分别从 A、B 同时出发,经几秒钟∆BPQ 与∆BAC 相似?
21、提 出 问 题 :
(1) 如 图 1,在 正 方 形 ABCD 中 ,点 E,H 分 别 在 BC ,AB 上 ,若 AE ⊥ DH 于 点 O ,求 证 :
AE = DH ; 类 比 探 究 :
(2) 如 图 2, 在 正 方 形 ABCD 中 , 点 H, E, G , F 分 别 在 AB , BC , CD , DA 上 , 若 EF
⊥ HG 于 点 O, 探 究 线 段 EF 与 HG 的 数 量 关 系 , 并 说 明 理 由 ; 综 合 运 用 :
(3) 在 (2 ) 问 条 件 下 , HF ∥ GE , 如 图 3 所 示 , 已 知 BE = EC = 2, EO = 2O F , 求 图 中 阴
影 部 分 的 面 积 .
新课 标 第 一 网
九年级第一学期数学期中测试卷
班级: 姓名: 得分:
一、选择题:(每小题 3 分,共计 30 分)
1、下列图形中,既是轴对称图形,又是中心对称图形的是( ).
A B C D
2、用配方法解方程 0522 xx 时,原方程应变形为( )
A. 61 2 x B. 61 2 x C. 92 2 x D. 92 2 x
3、如果关于 x 的一元二次方程 01)12(22 xkxk 有两个不相等的实数根,那么 k 的取值
范围是( )
A. k > 4
1 B. k > 4
1 且 0k C. k < 4
1 D. k
4
1 且 0k
4、已知关于 x 的一元二次方程 011 22 axxa 的一个根是 0,则 a 的值为( )
A.1 B. 1 C.1 或 1 D. 2
1
5、一个小组有若干人,新年互送贺卡一张,若全组共送贺卡 72 张,则这个小组共有( )
A.12 人 B.18 人 C.9 人 D.10 人 http://w ww.xkb 1.com
6、如图,△DEF 是由△ABC 绕点 O 旋转 180°而得到的,则下列结论不成立的是( )
A.点 A 与点 D 是对应点 B.BO=EO C.∠ACB=∠FDE D.AB∥DE
7、为了改善居民住房条件,某市计划用未来两年的时间,将城镇居民的住房面积由现在的人
均 10m2 提高到 12.1m2,若每年的年增长率相同,则年增长率为( )
A.9﹪ B.10﹪ C.11﹪ D.12﹪
8、抛物线 122 mmxxy 的图像经过原点,则 m 为( )
A.±1 B.-1 C.1 D.0
9、如图,已知点 O 是等边△ABC 三条高的交点,现将△AOB 绕点 O 旋转,要使旋转后能与
△BOC 重合,则旋转的最小角度为( )
A.60° B.120° C.240° D.360°
10、二次函数 362 xkxy 的图像与 x 轴有公共点,则 k 的取值范围是( )
A.k<3 B.k<3 且 k≠0 C.k≤3 D.k≤3 且 k≠0
二、填空题:(每小题 3 分,共计 18 分)X k B 1 . c o m
11、将点 A(3,1)绕原点 O 按顺时针方向旋转 90°到点 B,则点 B 的坐标是
12、二次函数 3)5(2 2 xy 的顶点坐标是
13、已知点 A(x1,y1),B(x2,y2)在二次函数 1)1( 2 xy 的图像上,若 x1<x2<1,则 y1 y2.
(填“>”“=”或“<”)
14、点 A(a,3)与点 B(- 4,b)关于原点对称,则 a+b= 。
15、如图所示,△OAB 绕点 O 逆时针旋转 80°得到△OCD,若∠A=110°,∠D=40°,则∠
α的度数为 。
16、矩形的周长为 20cm,当矩形的长为 cm 时,面积有最大值是 cm2。
三、解答题:
17、解方程:(每小题 4 分,共计 12 分)
(1)、 093 2 x (2)、 1222 xxx (3)、 83211 xxx
X K b1 .C om
18、(8 分)已知一条抛物线的顶点坐标为(- 2,1),且过点(2,7)。
(1)、求此抛物线的解析式;
(2)、试说明将抛物线 2axy 经过怎样的平移可以得到此抛物线的图像。
http://w ww.xkb 1.com
19、(12 分)如图所示的正方形网格中,△ABC 的顶点均在格点上,请在所给直角坐标系中
按要求画图和解答下列问题:
(1)以 A 点为旋转中心,将△ABC 绕点 A 顺时针旋转 90°得△AB1C1,画出△AB1C1;
(2)作出△ABC 关于坐标原点 O 成中心对称的△A2B2C2;(3)作出点 C 关于 x 轴的对称点 P。
若点 P 向右平移 x(x 取整数)个单位长度后落在△A2B2C2 的内部,请直接写出 x 的值。
20、(8 分)某商场将每件进价为 80 元的某种商品原来按每件 100 元出售,一天可售出 100
件,后来经过市场调查,发现这种商品的单价每降低 1 元,其销售量可增加 10 件。
(1)求商场经营该商品原来一天可获利润多少元?
(2)该商品降价后,若商场经营该商品一天要获利润 2160 元,则每件商品应降价多少元?
21、(12 分)心理学家发现,学生对概念的接受能力 y 与提出概念所用的时间 x(单位:分钟)
之间满足函数解析式 )300(436.21.0 2 xxxy ,y 值越大,表示接受能力越强。
(1)在直角坐标系中,画出该函数的图象;
(2)在什么范围内,学生的接受能力逐步增强?在什么范围内,学生的接受能力逐步降低?
(3)第 10 分钟时,学生的接受能力是多少?
Y
X
C
O
A
B
Y
XO
塔什店中学 2014-2015 学年九年级数学上学期期中测试卷答案
1、D 2、B 3、B 4、B 5、C 6、C 7、B 8、A 9、B 10、D
11、(1,- 3) 12、(5,3) 13、> 14、1 15、50° 16、5
17、(1)x1=0,x2=6 (2)x1= 52 ,x2= 52 (3)x1=1,x2=-3
18、(1)
2
5
2
3
8
31)2(8
3 22 xxxy
(2)把 2
8
3 xy 向左平移 2 个单位,向上平移 1 个单位,即可得到
2
5
2
3
8
3 2 xxy
19、(1)画出△AB1C1
(2)作出△A2B2C2
(3)作出 P 点。x 的值为 6 或 7.
Y
A2
P
C2
B2
C1
B1
X
C
O
A
B
●
20、解:(1)若商场经营该商品不降价,则一天可获利润为 100(100-80)=2000(元)
(2)设每件商品应降价 x 元,依题意,得(100-80-x)(100+10x)=2160,
即 x2-10x+16=0,解得 x1=2,x2=8,易知 x1=2,x2=8 都符合实际情况。
故若商场经营该商品一天要获利润 2160 元,则每件商品应降价 2 元或 8 元。
21、(1)图略
(2)函数 9.59)13(1.0436.21.0 22 xxxy ,当 0≤x≤13 时,学生的接受能力逐步
增强;当 13<x≤30 时,学生的接受能力逐步降低。
(3)当 x=10 时, 5943106.2101.0436.21.0 22 xxy ,即第 10 分钟时,学
生的接受能力是 59.
九年级上学期数学期末检测试卷附参考答案
一、选择题(本大题共 8 个小题,每题只有一个正确的选项,每小题 3 分,满分 24 分)
1.一元二次方程 042 x 的解是( )
A. 2x B. 2x
C. 21 x , 22 x D. 21 x , 22 x
2.二次三项式 2 4 3x x 配方的结果是( )
A. 2( 2) 7x B. 2( 2) 1x
C. 2( 2) 7x D. 2( 2) 1x
3.小明从上面观察下图所示的两个物体,看到的是( )
A B C D
4.人离窗子越远,向外眺望时此人的盲区是( )
A.变小 B.变大 C.不变 D.以上都有可能
5.函数
x
ky 的图象经过(1,-1),则函数 2 kxy 的图象是( )
6.在 Rt△ABC 中,∠C=90°,a=4,b=3,则 sinA 的值是( )
A. 5
4 B. 3
5 C. 4
3 D. 4
5
7.下列性质中正方形具有而矩形没有的是( )
A.对角线互相平分 B.对角线相等
C.对角线互相垂直 D.四个角都是直角
8.一只小狗在如图的方砖上走来走去,最终停在阴影方砖上的概率是( )
A.
15
4 B.
3
1
C.
5
1 D.
15
2
二、填空题(本大题共 7 个小题,每小题 3 分,满分 21 分)
9.计算 tan60°= .
10.已知函数 2 2( 1) my m x 是反比例函数,则 m 的值为 .
11.若反比例函数
x
ky 的图象经过点(3,-4),则此函数在每一个象限内
得 分 评卷人
正面
2
2 2
2
-2
-2
-2
-2O OOO
y y y y
xx x x
A B C D
y 随 x 的增大而 .
12.命题“直角三角形两条直角边的平方和等于斜边的平方”的逆命题是
.
13.有两组扑克牌各三张,牌面数字分别为 2,3,4,随意从每组中牌中抽取一张,数字和
是 6 的概率是 .
14.依次连接矩形各边中点所得到的四边形是 .
15.如图,在△ABC 中,BC = 8 cm,AB 的垂直平分线交
AB 于点D,交边 AC 于点 E,△BCE 的周长等于 18 cm,
则 AC 的长等于 cm.
三、解答题(本大题共 9 个小题,满分 75 分)
16.(本小题 6 分)解方程: 3 ( 3)x x x
17.(本小题 6 分)如图,楼房和旗杆在路灯下的影子如图所示。试确定路灯灯炮的位置,再
作出小树在路灯下的影子.(不写作法,保留作图痕迹)
18.(本小题 8 分)如图所示,课外活动中,小明在离旗杆 AB 的 10 米 C 处,用测角仪测得
旗杆顶部 A 的仰角为 40,已知测角仪器的高 CD=1.5 米,求旗杆 AB 的高.(精确到 0.1
得 分 评卷人
A
D
B C
E
米)
(供选用的数据:sin 40 0.64 ,cos40 0.77 , tan 40 0.84 )
19.(本小题 8 分)小明和小刚用如图的两个转盘做游戏,游戏规则如下:分别旋转两个转盘,
当两个转盘所转到的数字之积为奇数时,小明得 2 分;当所转到的数字之积为偶数时,
小刚得 1 分.这个游戏对双方公平吗?
转盘 1 转盘 2
20.(本小题 10 分)如图,平行四边形 ABCD 中,AE⊥BD,CF⊥BD,
垂足分别为 E、F.
(1)写出图中每一对你认为全等的三角形;
(2)选择(1)中的任意一对进行证明.
40 ED
C B
A
1 2 1
2
3
A
B C
D
E
F
21.(本小题 8 分)某水果商场经销一种高档水果,如果每千克盈利 10 元,每天可售出 500
千克,经市场调查发现,在进货价不变的情况下,出售价格每涨价 1 元,日销售量将减少 20
千克,现该商场要保证每天盈利 6000 元,同时又要使顾客得到实惠,那么每千克应涨价多少
元?
22.(本小题 10 分)已知:如图,D 是△ABC 中 BC 边上一点,E 是 AD 上的一点, EB=EC,
∠1=∠2.
求证:AD 平分∠BAC.
证明:在△AEB 和△AEC 中,
EB=EC
1= 2
AE=AE
∴△AEB≌△AEC(第一步)
∴∠BAE=∠CAE (第二步)
21
A
B C
D
E
∴ AD 平分∠BAC(第三步)
问:上面证明过程是否正确?若正确,请写出题中标出的每一步推理根据;若不正确,
请指出错在哪一步?并写出你认为正确的推理过程.
23.(本小题 9 分)正比例函数 kxy 和反比例函数
x
ky 的图象相交于 A,B 两点,已知点 A
的横坐标为 1,纵坐标为3.
(1)写出这两个函数的表达式;
(2)求 B 点的坐标;
(3)在同一坐标系中,画出这两个函数的图象.
O 1 2 3 4 5 6
6
5
4
3
2
1
-1-2-3-4-5-6 -1
-2
-3
-4
x
y
24.(本小题 10 分)阅读探索:“任意给定一个矩形 A,是否存在另一个矩形 B,它的周长和
面积分别是已知矩形周长和面积的一半?”(完成下列空格)
(1)当已知矩形 A 的边长分别为 6 和 1 时,小亮同学是这样研究的:
设所求矩形的两边分别是 yx和 ,由题意得方程组:
3
2
7
xy
yx ,
消去 y 化简得: 0672 2 xx ,
∵△=49-48>0,∴x1= ,x2= .
∴满足要求的矩形 B 存在.
(2)如果已知矩形 A 的边长分别为 2 和 1,请你仿照小亮的方法研究是否存在满足要求的矩
形 B.
(3)如果矩形 A 的边长为 m 和 n,请你研究满足什么条件时,矩形 B 存在?
2008-2009 学年上学期期末检测
九年级数学 参考答案
一、选择题(本大题共 8 个小题,每题只有一个正确的选项,每小题 3 分,满分 24 分)
1.C 2.B 3.A 4.B 5.A 6.D 7.C 8.B
二、填空题(本大题共 7 个小题,每小题 3 分,满分 21 分)
9. 3 10.-1 11.增大 12.如果三角形两边的平方和等于第三边的平方,那么这个
三角形是直角三角形 13. 1
3 14.菱形 15.10
三、解答题(本大题共 9 个小题,满分 75 分)
16.(本小题 6 分) 解方程得 x1=1,x2=3
17.(本小题 6 分) 略
18.(本小题8分)
解:在 Rt△ADE 中, tan ADE=
DE
AE
∵ DE=10, ADE=40°
∴ AE=DE tan ADE =10 tan 40°≈10 0.84 =8.4
∴ AB=AE+EB=AE+DC=8.4 1.5 9.9
答:旗杆 AB 的高为9.9 米
19.(本小题 8 分)
解:∵P(奇数)=
3
1 P(偶数)=
3
2
∵
3
1 ×2=
3
2 ×1
∴这个游戏对双方是公平的
20.(本小题 10 分)
解:(1)△ABD≌△CDB,△AEB≌△CFD,△AED≌△CFB
(2)证明略
21.(本小题 8 分)
转盘 2
转盘 1 1 2 3
1 1 2 3
2 2 4 6
解:设每千克应涨价 x 元,根据题意,得
(10 )(500 20 ) 6000x x 即 2 15 50 0x x , 解得 x1=5,x2=10
∵要使顾客得到实惠 ∴ 102 x 舍去 答:每千克应涨价 5 元。
22.(本小题 10 分)
解:上面的证明过程不正确,错在第一步。
证明:∵EB=EC, ∴∠3=∠4 又∵∠1=∠2
∴∠1+∠3=∠2+∠4 即∠ABC=∠ACB
∴AB=AC
∴在△AEB 和△AEC 中,
EB=EC
1= 2
AB=AC
∴△AEB≌△AEC
∴∠BAE=∠CAE
∴AD 平分∠BAC
23.(本小题 9 分)
解:(1)∵正比例函数 y=kx 与反比例函数
x
ky 的图像都过点 A(1,3),则 k=3
∴正比例函数是 y=3x ,反比例函数是 3y x
(2)∵点 A 与点 B 关于原点对称,∴点 B 的坐标是(-1,-3)
(3)略
24.(本小题 10 分)
解:(1)2 和 3
2
;
(2)
3
2
1
x y
xy
,消去 y 化简得:2 x2-3x+2=0,Δ=9-16<0,所以不存在矩形 B.
(3)(m + n)2 -8 mn≥0,
设所求矩形的两边分别是 yx和 ,由题意得方程组:
2
2
m nx y
mnxy
,消去 y 化简得:2 x2-(m + n)x + mn = 0,
Δ=(m + n)2 -8 mn≥0.
即(m + n)2-8 mn≥0 时,满足要求的矩形 B 存在
21
A
B C
D
E
3 4
九年级数学上学期期末检测试卷附参考答案 3 套
(全卷满分 120 分,考试时间 120 分钟)
一、选择题(本大题共 8 个小题,每题只有一个正确的选项,每小题 3 分,满分 24 分)
1.一元二次方程 042 x 的解是( )
A. 2x B. 2x
C. 21 x , 22 x D. 21 x , 22 x
2.二次三项式 2 4 3x x 配方的结果是( )
A. 2( 2) 7x B. 2( 2) 1x
C. 2( 2) 7x D. 2( 2) 1x
3.小明从上面观察下图所示的两个物体,看到的是( )
A B C D
4.人离窗子越远,向外眺望时此人的盲区是( )
A.变小 B.变大 C.不变 D.以上都有可能
5.函数
x
ky 的图象经过(1,-1),则函数 2 kxy 的图象是( )
6.在 Rt△ABC 中,∠C=90°,a=4,b=3,则 sinA 的值是( )
A. 5
4 B. 3
5 C. 4
3 D. 4
5
7.下列性质中正方形具有而矩形没有的是( )
A.对角线互相平分 B.对角线相等
C.对角线互相垂直 D.四个角都是直角
正面
2
2 2
2
-2
-2
-2
-2O OOO
y y y y
xx x x
A B C D
8.一只小狗在如图的方砖上走来走去,最终停在阴影方砖上的概率是( )
A.
15
4 B.
3
1
C.
5
1 D.
15
2
二、填空题(本大题共 7 个小题,每小题 3 分,满分 21 分)
9.计算 tan60°= .
10.已知函数 2 2( 1) my m x 是反比例函数,则 m 的值为 .
11.若反比例函数
x
ky 的图象经过点(3,-4),则此函数在每一个象限内
y 随 x 的增大而 .
12.命题“直角三角形两条直角边的平方和等于斜边的平方”的逆命题是
.
13.有两组扑克牌各三张,牌面数字分别为 2,3,4,随意从每组中牌中抽取一张,数字和
是 6 的概率是 .
14.依次连接矩形各边中点所得到的四边形是 .
15.如图,在△ABC 中,BC = 8 cm,AB 的垂直平分线交
AB 于点D,交边 AC 于点 E,△BCE 的周长等于 18 cm,
则 AC 的长等于 cm.
三、解答题(本大题共 9 个小题,满分 75 分)
16.(本小题 6 分)解方程: 3 ( 3)x x x
17.(本小题 6 分)如图,楼房和旗杆在路灯下的影子如图所示。试确定路灯灯炮的位置,再
得 分 评卷人
得 分 评卷人
A
D
B C
E
作出小树在路灯下的影子.(不写作法,保留作图痕迹)
18.(本小题 8 分)如图所示,课外活动中,小明在离旗杆 AB 的 10 米 C 处,用测角仪测得
旗杆顶部 A 的仰角为 40,已知测角仪器的高 CD=1.5 米,求旗杆 AB 的高.(精确到 0.1
米)
(供选用的数据:sin 40 0.64 ,cos40 0.77 , tan 40 0.84 )
19.(本小题 8 分)小明和小刚用如图的两个转盘做游戏,游戏规则如下:分别旋转两个转盘,
当两个转盘所转到的数字之积为奇数时,小明得 2 分;当所转到的数字之积为偶数时,
小刚得 1 分.这个游戏对双方公平吗?
40 ED
C B
A
1 2 1
2
3
转盘 1 转盘 2
20.(本小题 10 分)如图,平行四边形 ABCD 中,AE⊥BD,CF⊥BD,
垂足分别为 E、F.
(1)写出图中每一对你认为全等的三角形;
(2)选择(1)中的任意一对进行证明.
21.(本小题 8 分)某水果商场经销一种高档水果,如果每千克盈利 10 元,每天可售出 500
千克,经市场调查发现,在进货价不变的情况下,出售价格每涨价 1 元,日销售量将减少 20
千克,现该商场要保证每天盈利 6000 元,同时又要使顾客得到实惠,那么每千克应涨价多少
元?
A
B C
D
E
F
22.(本小题 10 分)已知:如图,D 是△ABC 中 BC 边上一点,E 是 AD 上的一点, EB=EC,
∠1=∠2.
求证:AD 平分∠BAC.
证明:在△AEB 和△AEC 中,
EB=EC
1= 2
AE=AE
∴△AEB≌△AEC(第一步)
∴∠BAE=∠CAE (第二步)
∴ AD 平分∠BAC(第三步)
问:上面证明过程是否正确?若正确,请写出题中标出的每一步推理根据;若不正确,
请指出错在哪一步?并写出你认为正确的推理过程.
23.(本小题 9 分)正比例函数 kxy 和反比例函数
x
ky 的图象相交于 A,B 两点,已知点 A
的横坐标为 1,纵坐标为3.
21
A
B C
D
E
(1)写出这两个函数的表达式;
(2)求 B 点的坐标;
(3)在同一坐标系中,画出这两个函数的图象.
24.(本小题 10 分)阅读探索:“任意给定一个矩形 A,是否存在另一个矩形 B,它的周长和
面积分别是已知矩形周长和面积的一半?”(完成下列空格)
(1)当已知矩形 A 的边长分别为 6 和 1 时,小亮同学是这样研究的:
设所求矩形的两边分别是 yx和 ,由题意得方程组:
3
2
7
xy
yx ,
O 1 2 3 4 5 6
6
5
4
3
2
1
-1-2-3-4-5-6 -1
-2
-3
-4
-5
-6
x
y
消去 y 化简得: 0672 2 xx ,
∵△=49-48>0,∴x1= ,x2= .
∴满足要求的矩形 B 存在.
(2)如果已知矩形 A 的边长分别为 2 和 1,请你仿照小亮的方法研究是否存在满足要求的矩
形 B.
(3)如果矩形 A 的边长为 m 和 n,请你研究满足什么条件时,矩形 B 存在?
2008-2009 学年上学期期末检测
九年级数学 参考答案
一、选择题(本大题共 8 个小题,每题只有一个正确的选项,每小题 3 分,满分 24 分)
1.C 2.B 3.A 4.B 5.A 6.D 7.C 8.B
二、填空题(本大题共 7 个小题,每小题 3 分,满分 21 分)
9. 3 10.-1 11.增大 12.如果三角形两边的平方和等于第三边的平方,那么这个
三角形是直角三角形 13. 1
3 14.菱形 15.10
三、解答题(本大题共 9 个小题,满分 75 分)
16.(本小题 6 分) 解方程得 x1=1,x2=3
17.(本小题 6 分) 略
18.(本小题8分)
解:在 Rt△ADE 中, tan ADE=
DE
AE
∵ DE=10, ADE=40°
∴ AE=DE tan ADE =10 tan 40°≈10 0.84 =8.4
∴ AB=AE+EB=AE+DC=8.4 1.5 9.9
答:旗杆 AB 的高为9.9 米
19.(本小题 8 分)
解:∵P(奇数)=
3
1 P(偶数)=
3
2
∵
3
1 ×2=
3
2 ×1
∴这个游戏对双方是公平的
20.(本小题 10 分)
解:(1)△ABD≌△CDB,△AEB≌△CFD,△AED≌△CFB
(2)证明略
21.(本小题 8 分)
解:设每千克应涨价 x 元,根据题意,得
(10 )(500 20 ) 6000x x 即 2 15 50 0x x , 解得 x1=5,x2=10
∵要使顾客得到实惠 ∴ 102 x 舍去 答:每千克应涨价 5 元。
22.(本小题 10 分)
解:上面的证明过程不正确,错在第一步。
证明:∵EB=EC, ∴∠3=∠4 又∵∠1=∠2
∴∠1+∠3=∠2+∠4 即∠ABC=∠ACB
∴AB=AC
∴在△AEB 和△AEC 中,
EB=EC
1= 2
AB=AC
∴△AEB≌△AEC
∴∠BAE=∠CAE
∴AD 平分∠BAC
23.(本小题 9 分)
解:(1)∵正比例函数 y=kx 与反比例函数
x
ky 的图像都过点 A(1,3),则 k=3
∴正比例函数是 y=3x ,反比例函数是 3y x
(2)∵点 A 与点 B 关于原点对称,∴点 B 的坐标是(-1,-3)
(3)略
转盘 2
转盘 1 1 2 3
1 1 2 3
2 2 4 6
21
A
B C
D
E
3 4
24.(本小题 10 分)
解:(1)2 和 3
2
;
(2)
3
2
1
x y
xy
,消去 y 化简得:2 x2-3x+2=0,Δ=9-16<0,所以不存在矩形 B.
(3)(m + n)2 -8 mn≥0,
设所求矩形的两边分别是 yx和 ,由题意得方程组:
2
2
m nx y
mnxy
,消去 y 化简得:2 x2-(m + n)x + mn = 0,
Δ=(m + n)2 -8 mn≥0.
即(m + n)2-8 mn≥0 时,满足要求的矩形 B 存在
九年级数学上学期期末检测试题卷
(全卷满分 120 分,考试时间 120 分钟)
一、选择题(本大题共 8 个小题,每题只有一个正确的选项,每小题 3 分,满分 24 分)
1.下列方程中,是一元二次方程的是( )
A. 32 yx B. 2( 1) 3x
C. 113 22 xxx D. 2 9x
2.有一实物如下左图,那么它的主视图是( )
3.到三角形各顶点的距离相等的点是三角形( )
A.三条角平分线的交点 B.三条高的交点
C.三边的垂直平分线的交点 D.三条中线的交点
4.甲、乙两地相距 60km,则汽车由甲地行驶到乙地所用时间 y(小时)与行驶速度 x(千米/时)之间的
函数图像大致是( )
A B C D
O x
y
A
O x
y
B
O x
y
C
O x
D
y
5.下列命题中,不正确的是( )
A.顺次连结菱形各边中点所得的四边形是矩形 B.有一个角是直角的菱形是正方形
C.对角线相等且垂直的四边形是正方形 D.有一个角是 60°的等腰三角形是等边三角形
6.在 Rt△ABC 中,∠C=90°,a=4,b=3,则 sinA 的值是( )
A. 4
5 B. 3
5 C. 4
3 D. 5
4
7.电影院呈阶梯或下坡形状的主要原因是( )
A.为了美观 B.减小盲区 C.增大盲区 D.盲区不变
8.某校九年级一班共有学生 50 人,现在对他们的生日(可以不同年)进行统计,则正确的说法是( )
A.至少有两名学生生日相同 B.不可能有两名学生生日相同
C.可能有两名学生生日相同,但可能性不大 D.可能有两名学生生日相同,且可能性很大
二、填空题(本大题共 7 个小题,每小题 3 分,满分 21 分)
9.计算 2cos60°+ tan245°= 。
10.一元二次方程 2 3 0x x 的解是 。
11.请你写出一个反比例函数的解析式使它的图象在第一、三象限 。
12.在平行四边形 ABCD 中,对角线 AC 长为 10 cm ,∠CAB=30°,AB= 6 cm ,则平行四边形 ABCD 的面积
为 2cm 。
13.命题“等腰梯形的对角线相等”。它的逆命题是 .
14.随机掷一枚均匀的硬币两次,至少有一次正面朝上的概率是 。
15 . 已 知 反 比 例 函 数 ky x
的 图 像 经 过 点 ( 1 , - 2 ), 则 直 线 y = ( k - 1 ) x 的 解 析 式
为 。
三、解答题(本大题共 9 个小题,满分 75 分)
16.(本小题 6 分)解方程: 0672 xx
17.(本小题 6 分)为响应国家“退耕还林”的号召,改变我省水土流失严重的状况,2005 年我省退耕还
林 1600 亩,计划 2007 年退耕还林 1936 亩,问这两年平均每年退耕还林的增长率是多少?
18.(本小题 6 分)如图,小明为测量某铁塔 AB 的高度,他在离塔底 B 的 10 米 C 处测得塔顶的仰角α=43°,
A
ED α
已知小明的测角仪高 CD=1.5 米,求铁塔 AB 的高。(精确到 0.1 米)
(参考数据:sin43° =0.6820, cos43° =0.7314, tan43° =0.9325)
19.(本小题 8 分)你吃过拉面吗?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉
面,面条的总长度 y(m)是面条的粗细(横截面积) s (mm2)的反比例函数,其图像如图所示。
(1)写出 y 与 s 的函数关系式;
(2)求当面条粗 1.6mm2 时,面条的总长度是多少米?
20.(本小题 8 分)两个布袋中分别装有除颜色外,其他都相同的 2 个白球,1 个黑球,同时从这两个布袋
中摸出一个球,请用列表法表示出可能出现的情况,并求出摸出的球颜色相同的概率。
21.(本小题 8 分)已知:四边形 ABCD 的对角线 AC、BD 相交于点 O,给出下列 5 个条件:
①AB∥DC;②OA=OC;③AB=DC;④∠BAD=∠DCB;⑤AD∥BC。
(1)从以上 5 个条件中任意选取 2 个条件,能推出四边形 ABCD 是平行四边形的有(用序号表示):
如①与⑤ 、 。(直接在横线上再写出两种)
(2)对由以上 5 个条件中任意选取 2 个条件,不能推出四边形 ABCD 是平行四边形的,请选取一种情
形举出反例说明。
22.(本小题 9 分)在如图所示的三角形纸片 ABC 中,∠C=90°,∠B=30°,按如下步骤可以把这个直角
三角形纸片分成三个全等的小直角三角形(图中虚线表示折痕)。①先将点 B 对折到点 A,②将对折后
的纸片再沿 AD 对折。
(1)由步骤①可以得到哪些等量关系?
A
B
D
O
C
1
20
s(mm2)
y(m)
O 2 3 4 5
P(4,32)
60
40
80
100
A
C
E
D B
(2)请证明△ACD≌△AED
(3)按照这种方法能否将任意一个直角三角形分成三个全等的小三角形?
23.(本小题 12 分)如图,已知直线 y =-x+4 与反比例函数 y k
x
的图象相交于点 A(-2,a),并且与 x
轴相交于点 B。
(1)求 a 的值;
(2)求反比例函数的表达式;
(3)求△AOB 的面积。
24.(本小题 12 分)阅读下面材料,再回答问题:
有一些几何图形可以被某条直线分成面积相等的两部分,我们将“把一个几何图形分成面积相等的两
部分的直线叫做该图形的二分线”,如:圆的直径所在的直线是圆的“二分线”,正方形的对角线所在的直
线是正方形的“二分线”。
解决下列问题:
(1)菱形的“二分线”可以是 。
(2)三角形的“二分线”可以是 。
(3)在下图中,试用两种不同的方法分别画出等腰梯形 ABCD 的“二分线”.
A D A D
B C B C
x
y
A
O
B
新街中学 2008-2009 学年度上学期期末检测答题卷
九年级数学(答题卡)
一、选择题(每小题 3 分,共 24 分)
题号 1. 2. 3. 4. 5. 6. 7. 8.
答案
二、填空题(每题 3 分,共 21 分)
9. ; .
10. . 11. . 12. 2cm .
13. .
14. . 15. .
三、解答题(共 75 分)
16.(6 分) 解方程: 0672 xx 17. (6 分)
解: 解:
(18 题图)
18.(6 分)解:
(19 题图)
19. (8 分)解:(1)
20. (8 分)解:
(2)
21. (8 分)解:(1)如①与⑤ 、 。(直接在横线上再写出两
种).
C
A
B
ED α
1
20
s(mm2)
y(m)
O 2 3 4 5
P(4,32)
60
40
80
100
(2) .
(21 题图)
22.( 9 分)解:
(1) .
(2)证明:
(22 题图)
(3) .
23. (12 分)解:(1) (2)解:
(3)解:
24. (12)分解:
(1)菱形的“二分线”可以是 。
(2)三角形的“二分线”可以是 。
(3)在下图中,试用两种不同的方法分别画出等腰梯形 ABCD 的“二分线”。
九年级数学(参考答案)
一、选择题(本大题共 8 个小题,每题只有一个正确的选项,每小题 3 分,满分 24 分)
A
B
D
O
C
A
C
C
E
D B
A D A D
B C B C
1.D 2.A 3.C 4.B 5.C 6.A 7.B 8.D
二、填空题(本大题共 7 个小题,每小题 3 分,满分 21 分)
9.2 10.x1=0, x2=3 11. 2y x
…… 12.30
13.对角线相等的梯形是等腰梯形 14. 1
4 15.y =-3x
三、解答题(本大题共 9 个小题,满分 75 分)
16.(本小题 6 分)
解方程得 x1=1,x2=6
17.(本小题 6 分)
解: 设平均增长率为 x ,则
1600(1+x)2=1936 解得:x1=0.1=10% x2=-2.1(舍去)
18.(本小题6分)
解:如图,可知四边形DCBE是矩形,
则EB = DC =1.5米,DE=CB=10米
在 Rt△AED 中,∠ADE=α=43º
那么tanα AE
DE
所以,AE=DEtan43º =10×0.9325=9.325
所以,AB=AE+EB =9.325+1.5=10.825≈10.8(米)
19.(本小题 8 分)
解:(1)设 y 与 s 的函数关系式为
s
ky ,
将 s=4,y=32 代入上式,解得 k=4×32=128
所以 y 与 s 的函数关系式
sy 128
(2)当 s=1.6 时, 806.1
128 y
所以当面条粗 1.6mm2 时,面条的总长度是 80 米
20.(本小题 8 分)列表得:
白球的概率= 4
9
黑球的概率= 1
9
21.(本小题 8 分)
解:(1)①与②;①与③;①与④;②与⑤;④与⑤
(只要写出两组即可;每写一个给 2 分)
(2)③与⑤ 反例:等腰梯形
22.(本小题 9 分)
解:(1)AE=BE,AD=BD,∠B=∠DAE=30º,
∠BDE=∠ADE=60º,∠AED=∠BED=90º。
(2)在 Rt△ABC 中,∠B=30º,所以 AE=EB,因而 AC=AE
又因为∠CAD=∠EAD,AD=AD 所以△ACD≌△AED
C
A
B
ED α
,
,
,,
,
,
,
,
,
( )
( )
( )
( )
( )
( )
( )
( ) 黑
黑
黑
( )
黑黑黑黑
黑
白
白白
白
白
白白白
白
白
白白
白
白
白白
袋2 袋1
A D
B C
(3)不能
23.(本小题 12 分)
解:(1)将 A(-2,a)代入 y=-x+4 中,得:a=-(-2)+4 所以 a =6
(2)由(1)得:A(-2,6)
将 A(-2,6)代入
x
ky 中,得到
26 k 即 k=-12
所以反比例函数的表达式为:
xy 12
(3)如图:过 A 点作 AD⊥x 轴于 D;
因为 A(-2,6) 所以 AD=6
在直线 y=-x+4 中,令 y=0,得 x=4
所以 B(4,0) 即 OB=4
所以△AOB 的面积 S= 2
1 OB×AD= 2
1 ×4×6=12
24.(本小题 12 分)
解:(1)菱形的一条对角线所在的直线。(或菱形的一组对边的中点所在的直线或菱形对角线
交点的任意一条直线)。
(2)三角形一边中线所在的直线。
(3)方法一:取上、下底的中点,过两点作直线得梯形的二分线(如图 1)
方法二:过 A、D 作 AE⊥BC,DF⊥BC,垂足 E、F,连接 AF、DE 相交于 O,过点 O 任意
作直线即为梯形的二分线(如图 2)
(如图 1) (如图 2)
2009-2010 上学期期末检测试题卷
九年级数学
一、选择题(每小题 3 分,满分 24 分)
1.一元二次方程 2 5 6 0x x 的根是( )
A.x1=1,x2=6 B.x1=2,x2=3 C.x1=1,x2=-6 D.x1=-1,x2=6
2.下列四个几何体中,主视图、左视图与俯视图是全等图形的几何体是( )
A D
B CE F
O
x
y
A
OD
B
A.球 B.圆柱 C.三棱柱 D.圆锥
3.到三角形三条边的距离相等的点是三角形( )
A.三条角平分线的交点 B.三条高的交点
C.三边的垂直平分线的交点 D.三条中线的交点
4.如果矩形的面积为 6cm2,那么它的长 y cm 与宽 x cm 之间的函数关系用图象表示
大致( )
A B C D
5.下列函数中,属于反比例函数的是( )
A.
3
xy B. 1
3y x
C. 5 2y x D. 2 1y x
6.在 Rt△ABC 中,∠C=90°,a=4,b=3,则 cosA 的值是( )
A. 4
5
B. 3
5
C. 4
3
D. 5
4
7.如图(1),△ABC 中,∠A=30°,∠C=90°AB 的垂直平分线 (1)
交 AC 于 D 点,交 AB 于 E 点,则下列结论错误的是( )
A、AD=DB B、DE=DC C、BC=AE D、AD=BC
8.顺次连结等腰梯形各边中点得到的四边形是 ( )
A、矩形 B、菱形 C、正方形 D、平行四边形
二、填空题(每小题 3 分,满分 21 分)
9.计算 tan45°= .
10.已知函数 2 2( 1) my m x 是反比例函数,则 m 的值为 .
11.请你写出一个反比例函数的解析式,使它的图象在第二、四象限 .
y
xO o
y
x
y
xo
y
xo
12.在直角三角形中,若两条直角边长分别为 6cm 和 8cm,则斜边上的中线长
为 cm.
13. 已知菱形的周长为 cm40 ,一条对角线长为 cm16 ,则这个菱形的面积
为 (cm)2.
14.已知正比例函数 kxy 与反比例函数 0 kx
ky 的一个交点是(2,3),则另
一个交点是( , ).
15.如图,已知 AC=DB,要使△ABC≌△DCB,需添加的一个
条件是 .
三、解答题(本大题共 9 个小题,满分 75 分)
16.(本小题 8 分)解方程: 2 ( 2)x x x
17.(本小题 8 分)如图,在△ABD 中,C 是 BD 上的一点,
且 AC⊥BD,AC=BC=CD.(1)求证:△ABD 是等腰三角形.
(2)求∠BAD 的度数.
18.(本小题 8 分)如图所示,课外活动中,小明在离旗杆 AB 的10米 C 处,用
测角仪测得旗杆顶部 A 的仰角为 40,已知测角仪器的高 CD=1.5米,求旗杆
AB 的高.(精确到0.1米)
(供选用的数据:sin 40 0.64 ,cos40 0.77 , tan 40 0.84 )
19.(本小题 8 分)某商店四月份的营业额为 40 万元,五月份的营业额比四月
份有所增长,六月份比五月份又增加了 5 个百分点,即增加了 5%,营业额达到
了 50.6 万元。求五月份增长的百分率。
20.(本小题 8 分)“一方有难,八方支援”.今年 11 月 2 日,鄂嘉出现洪涝灾害,
A
B C D
40 ED
C B
A
牵动着全县人民的心,医院准备从甲、乙、丙三位医生和 A、B 两名护士中
选取一位医生和一名护士支援鄂嘉防汛救灾工作.
(1)若随机选一位医生和一名护士,用树状图(或列表法)表示所有可能
出现的结果.
(2)求恰好选中医生甲和护士 A 的概率.
21.(本小题 8 分)如图,在△ABC 中,AC=BC,∠C=90°,AD 是△ABC 的角平分
线,DE⊥AB,垂足为 E.
(1)已知 CD=4cm,求 AC 的长.
(2)求证:AB=AC+CD.
22.(8 分)在如图的 12×24 的方格形纸中(每个小方格的边长都是 1 个单位)
有一ΔABC. 现先把ΔABC分别向右、向上平移8 个单位和3个单位得到ΔA1B1C1;
再以点 O 为旋转中心把ΔA1B1C1 按顺时针方向旋转 90º得到ΔA2B2C2. 请在所给
的方格形纸中作出ΔA1B1C1 和ΔA2B2C2.
23.(本题满分 9 分)
如图,给出四个等式:①AE=AD;②AB=AC;③OB=OC;④∠B=∠C. 现选取其中
的三个,以两个作为已知条件,另一个作为结论.
(1)请你写出一个正确的命题,并加以证明;
(2)请你至少写出三个这样的正确命题.
24、(10 分)如图,已知反比例函数
x
ky 2
和一次函数 y=2x-1,其中一次函数的
图象经过(a,b),(a+1,b+k)两点.
A
C
E
D B
C2
B2
A B
C
D
E O
(1)求反比例函数的解析式;
(2)如图 4,已知点 A 在第一象限,且同时在上述两个函数的图象上,求点 A
的坐标;
(3)利用(2)的结果,请问:在 x 轴上是否存在点 P,使△AOP 为等腰三
角形?若存在,把符合条件的 P 点坐标都求出来;若不存在,请说明
理由.
九年级数学参考答案
一、选择题(每小题 3 分,满分 24 分)
1.D 2.A 3.A 4.C 5.B 6.B 7.B 8.B
二、填空题(每小题 3 分,满分 21 分)
9.1 10.1 11. 1y x
…… 12.5 13.96 (cm)2 14.(-2,-3) 15.AB=DC 或 ACB= DBC
三、解答题(共 9 个小题,满分 75 分)
16.(8 分) 解方程得 x1=1,x2=2
17.(8 分)
解:(1)∵ AC⊥BD,AC=BC=CD ∴ ACB= ACD=90°
∴ △ACB≌△ACD ∴ AB=AD ∴ △ABD 是等腰三角形.
(2)∵ AC⊥BD,AC=BC=CD ∴ △ACB、△ACD 都是等腰直角三角形.
∴ B= D=45° ∴ BAD=90°
18.( 8分)
解:在 Rt△ADE 中, tan ADE=
DE
AE
∵ DE=10, ADE=40°
∴ AE=DE tan ADE =10 tan 40°≈10 0.84 =8.4
∴ AB=AE+EB=AE+DC=8.4 1.5 9.9
答:旗杆 AB 的高为9.9米
19.( 8 分解:设五月份增长率为 x
①
②
40(1+x)(1+x+5%)=50.6
解得 x1=0.1,x2=-2.15(舍去)
20.( 8 分)解:(1)用列表法或树状图表示所有可能结果如下:
列表法: 树状图:
(2) P (恰好选中医生甲和护士 A)= 1
6
, ∴恰好选中医生甲和护士 A 的概率是 1
6
21.(8 分)
解:(1)∵AD 是△ABC 的角平分线,DC⊥AC,DE⊥AB
∴DE=CD=4cm, 又∵AC=BC,∴∠B=∠BAC,
又∵∠C=90º,∴∠B=∠B DE=45º,∴BE=DE
在等腰直角三角形 BDE 中,由勾股定理得,BD=4 2 cm
∴AC=BC=CD+BD=4+4 2 (cm)
(2)由(1)的求解过程可知:△ACD≌△AED,
∴AC=AE, 又∵BE=DE=CD ∴AB=AE+BE=AC+CD
22.解:(8 分).ΔA1B1C1 和ΔA2B2C2 如图所示.
23.(9 分)(1)如果 AE=AD,AB=AC,那么∠B=∠C.
证明:在ΔABE 和ΔACD 中,
∵AE=AD,∠A=∠A,AB=AC,∴ΔABE≌ΔACD,∴∠B=∠C.
(2)①如果 AE=AD,AB=AC,那么 OB=OC.
②如果 AE=AD,∠B=∠C,那么 AB=AC.
③如果 OB=OC,∠B=∠C,那么 AE=AD.
24.(10 分)解:(1)由题意得
1)1(2
12
akb
ab
②-①得 2k ∴反比例函数的解析式为
xy 1 .
A B
甲 (甲, A) (甲, B)
乙 (乙, A) (乙, B)
丙 (丙, A) (丙, B)
护 士医生 C
(2)由
xy
xy
1
12
解得
1
1
1
1
y
x ,
2
2
1
2
2
y
x
∵点 A 在第一象限,∴点 A 的坐标为(1,1)
(3) 211 22 OA ,OA 与 x 轴所夹锐角为 45°,
①当 OA 为腰时,由 OA=OP 得 P1( 2 ,0),P2(- 2 ,0);由 OA=AP 得 P3=(2,0).
②当 OA 为底时,得 P4=(1,0).
∴符合条件的点有 4 个,分别是( 2 ,0),(- 2 ,0),(2,0),(1,0)
九年级数学上册半期考试测试题
姓名: 班级: 学号: 总分:
一、选择题
1、下面的 5 个字母中,是中心对称图形的有 ( )
C H I N A
A、2 个 B、3 个 C、4 个 D、5 个
2、一元二次方程 0532 xx 的根的情况是( )
A、有两个不相等的实数根 B、有两个相等的实数根
C、没有实数根 D、无法判断
3、将抛物线 2)1( 2 xy 向下平移 2 个单位,再向右平移 3 个单位,所得到的抛物线是( )
A、 4)4( 2 xy B、 2)2( xy C、 4)2( 2 xy D、 4)2( 2 xy
4、已知关于 x 的一元二次方程 2 2 0x x a 有实数根,则实数 a 的取值范围是( )
A、a≤1 B、a<1 C、a≤-1 D、 a≥1
5、下列二次函数的图象与 x 轴有两个不同的交点的是( )
A、 2xy B、 42 xy C、 523 2 xxy D、 153 2 xxy
6、二次函数 342 2 xxy 的图象( )X k B 1 . c o m
A、最高点在 )1,1( B、最高点在 )1,1( C、最低点在 )1,1( D、最低点在 )1,1(
7、若 1x 、 2x 是一元二次方程 0572 xx 的两根,则
21
11
xx
的值是( )
A、
5
7 B、
5
7 C、
7
5 D、
7
5
8、4 张扑克牌如图(1)所示放在桌子上,小敏把其中一张旋转 180°后得到如图(2)所示,
那么她所旋转的牌从左起是( )
A、第一张、第二张 B、第二张、第三张
C、第三张、第四张 D、第一张、第三张
(1) (2)
9、某商品原价 200 元,连续两次降价 a%后售价为 148 元,下列所列方程正确的是( )
A、 148%)1(200 2 a B、 148%)1(200 2 a C、 200%)1(148 2 a D、 200%)1(148 2 a
10 、 已 知 二 次 函 数 2 ( 0)y ax bx c a 的 图 象 如 图 所示 , 则 下 列 结 论 : 0abc ; ② 方 程
2 0ax bx c 的两根之和大于 0; y③ 随 x 的增大而增大;④ 0a b c ,其中正确的个数( )
A.4 个 B.3 个
C.2 个 D.1 个
二、填空题 X| k |B| 1 . c|O |m
11、在平面直角坐标系中,点 (2 3)P , 关于原点对称点 P的坐标是 。
12、方程 2 4x x 的解是_____________。
13、关于 x 的方程 0122 2 kxx 的一个根是-2,则方程的另一根是 ; k = 。
14、已知函数 cxxy 22 的部分图象经过点 )2,1( ,则 c ;当 时, y 随 x 的增大而减
小。http://ww w.xkb1.com
15、二次函数 182 2 xxy 的图象开口向 ,顶点坐标是 。
16、参加一次同学聚会,每两人都握一次手,所有人共握了 45 次,若设共有 x 人参加同学聚会。列方程
得 。
17、如图,将 Rt△ABC 绕 C 点逆时针旋转得到△ CBA ' ,若∠ CBA' =160°,则此图形旋转角是
度。
18、如图,将边长为 4 的正方形,沿两边剪去两个边长为 x 的矩形,剩余部分的面积为 9,可列出方程为
_____________。
19、 已知 ),3(),,3(),,4( 321 yCyByA 三点都在二次函数 2)2(2 xy
的图像上,则 321 ,, yyy 的大小关系为 。
20、已知二次函数 4)3( 2 xy ,当 32 x 时,函数的最大值是 。
第 18 题图
三、解答题 w W w .x K b 1.c o M
21、解下列方程:
(1) 0222 xx (2) 22 3)12(3)1( xxx (3) 0672 xx
22、如图,请在下列网格图中画出所给图形绕点 O 顺时针依次旋转 90°后所成的图形。新 课 标
第 一 网
23、某水果批发商销售每箱进价为 40 元的苹果,物价部门规定每箱售价不得高于 55 元,市场调查发现,
若每箱以 50 元的价格销售,平均每天售价 90 箱,价格每提高 1 元,平均每天少销售 3 箱。
(1)求平均每天销售量 y(箱)与销售价 x(元/箱)之间的函数解析式,并写出 x 的取值范围;
(2)求该批发商平均每天销售利润ω元与销售价 x(元/箱)之间的函数解析式;
(3)当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?xKb 1 . Com
O
24、
九年级数学上册期末测试题附参考答案
一、选择题(每小题 3 分,共 30 分)
1.下列关于 x 的方程中,是一元二次方程的有( )
A. 2
2 1
x
x B. 02 cbxax
C. 121 xx D. 0523 22 yxyx
2.化简
13
2
12
1
的结果为( )
A、 23 B、 23 C、 322 D、 223
3.已知关于 x 的方程 2 6 0x kx 的一个根为 3x ,则实数 k 的值为( )
A.2 B. 1 C.1 D. 2
4.要使二次根式 1x 有意义,那么 x 的取值范围是( )
(A)x>-1 (B) x<1 (C) x≥1 (D)x≤1
5.有 6 张写有数字的卡片,它们的背面都相同,现将它们 背 面 朝
上(如图 2),从中任意一张是数字 3 的概率是( )
A、
6
1 B、
3
1 C、
2
1 D、
3
2
6.已知 x、y 是实数, 3x+4 +y2-6y+9=0,则 xy 的值是( )
A.4 B.-4 C.9
4
D.-9
4
7、下列图形中,既是轴对称图形,又是中心对称图形的是( )
A B C D
8.已知两圆的半径分别是 5cm 和 4cm,圆心距为 7cm,那么这两圆的位置关系
图 2
图 3
图 7
是( )
A.相交 B.内切 C.外切 D.外离
9.如图 3,⊙O的半径为5,弦AB的长为8,M是弦AB上的动点,则线段OM长的最小
值为( )
A.2 B.3 C.4 D.5
10.已知:如图 4, ⊙O 的两条弦 AE、BC 相交于点 D,连接 AC、BE.
若∠ACB=60°,则下列结论中正确的是( )
A.∠AOB=60° B. ∠ADB=60°
C.∠AEB=60° D.∠AEB=30°
二、填空题(每小题 3 分,共 24 分)
11.方程 x 2 = x 的解是______________________
12.如图所示,五角星的顶点是一个正五边形的五个顶点.这个 五 角 星
可以由一个基本图形(图中的阴影部分)绕中心 O 至少经过
____________次旋转而得到, 每一次旋转_______度.
13.若实数 a 、 b 满 足
1
11 22
a
aab , 则 a+b 的 值 为
________.
14.圆和圆有不同的位置关系.与下图不同的圆和圆的位置关系是_____.(只填一种)
15 . 若 关于 x
方程 kx2–6x+1=0 有两个实数根,则 k 的取值范围是 .
16.如图 6,在 Rt△ABC 中,∠C=90°,CA=CB=2。分别以 A、B、C 为 圆
心,以
2
1 AC 为半径画弧,三条弧与边 AB 所围成的阴影部分的面积 是
______.
17.已知:如图 7,等腰三角形 ABC 中,AB=AC=4,若以 AB 为直径的⊙O 与 BC 相交于点 D,
DE∥AB,DE 与 AC 相交于点 E,则 DE=____________。
18. 如图,是一个半径为 6cm,面积为 12 cm2 的扇形纸片,现需要一个半径为 R 的
圆形纸片,使两张纸片刚好能组合成圆锥体,则 R 等于 cm
三.解答题
E
D
C
B
A
O
图 4
图 5
图 6
12 题图
O
R
游戏规则
随机抽取一张卡片,记
下数字放回,洗匀后再抽一
张.将抽取的第一张、第二
张卡片上的数字分别作为
十位数字和个位数字,若组
成的两位数不超过 32,则
小贝胜,反之小晶胜.
2 3 62
19.(6 分)计算: 1 3 2 29 45 3 210 36
. (6 分)解方程:2(x+2)2=x2-4
20(10 分)
如图 9 所示,每个小方格都是边长为 1 的正方形, 以 O 点
为坐标原点建立平面直角坐标系.
(1)画出四边形 OABC 关于 y 轴对称的四边形
OA1B1C1,并写出点 B1 的坐标是 .
(2)画出四边形OABC绕点O顺时针方向旋转90° 后 得 到
的四边形 OA2B2C2. 并写出点 B2 的坐标是 .
21(10 分)
四张质地相同的卡片如图所示. 将卡片洗匀后,背面朝上放置在桌面上.
(1)求随机抽取一张卡片,恰好得到数字 2 的概率;
(2)小贝和小晶想用以上四张卡片做游戏,游戏规则见信息图.你认为这个游戏公平吗?
请用列表法或画树状图法说明理由,若认为不公平,请你修改规则,使游戏变得公平.
22.(10 分)
某商场今年 2 月份的营业额为 400 万元,3 月份的营业额比 2 月份增加 10%,5 月份的营
业额达到 633.6 万元.求3月份到5月份营业额的月平均增长率.
23.(12 分)
如图 15,在 Rt△ABC 中,∠B=90°,∠A 的平分线交 BC 于 D,E 为 AB 上一点,DE=DC,以
D 为圆心,以 DB 的长为半径画圆。
求证:(1)AC 是⊙D 的切线;(2)AB+EB=AC。
24.(12 分)
高致病性禽流感是比 SARS 病毒传染速度更快的传染病。
(1)某养殖场有 8 万只鸡,假设有 1 只鸡得了禽流感,如果不采取任何防治措施,那么,到
第二天将新增病鸡 10 只,到第三天又将新增病鸡 100 只,以后每天新增病鸡数依次类推,
请问:到第四天,共有多少只鸡得了禽流感病?到第几天, 该 养 殖 场
所有鸡都会被感染?
(2)为防止禽流感蔓延,政府规定:离疫点 3 千米范围内 为扑杀区,
所有禽类全部扑杀;离疫点 3 至 5 千米范围内为免疫区, 所 有 的 禽
类强制免疫;同时,对扑杀区和免疫区内的村庄、道路实 行 全 封 闭
管理。现有一条笔直的公路 AB 通过禽流感病区,如图 11, O 为疫点,
在扑杀区内的公路 CD 长为 4 千米,问这条公路在该免疫区 内 有 多 少
千米?
图 11
图 15
期末摸拟测试题(一)
一、选择题
1.C 2.A 3.C 4.C 5.C 6.B 7 .B 8.A 9.C 10.C
二、填空题
11. 1,0 21 xx 13.四、72 13.1 14.相切(内切或外切) 15.k ≤9 且 k
≠0 16.
22 17.2 18. 2
三、解答题
19.1). 43 2 2).x1=-2,x2=-6
20.略
21.(1)0.5
(2)树形图(略) 5 3
8 8
≠ 不公平 修改规则(略)
22.解:设3月份到5月份营业额的月平均增长率为 x,由题意列方程得
6.633)1%)(101(400 2 x ,
解得 ),(2.1%,1202.1 21 舍去不合题意 xx 。
答:3月份到5月份营业额的月平均增长率为 120%。
23.略
24.解:(1)由题意可知,到第 4 天得禽流感病鸡数为 1+10+100+1000=1111,到第 5 天得禽
流感病鸡数为 10000+1111=11111,到第 6 天得禽流感病鸡数为 100000+11111>80000。所以
到第 6 天所有的鸡都会被感染。
(2)过点 O 作 OE⊥CD 交 CD 于点 E,连接 OC、OA,∵OA=5,OC=3,CD=4,∴CE=2。
在 Rt△OCE 中,AE= 5222 OEOA ,∴AC=AE-CE= 252 ,∵AC=BD,
∴AC+BD= 454 。答:这条公路在该免疫区内有( 454 )千米。