沪教版（上海）数学七年级第二学期-14比较、归纳、提炼、升华 ——从教材例、习题谈《三角形》复习

沪教版（上海）数学七年级第二学期-14比较、归纳、提炼、升华 ——从教材例、习题谈《三角形》复习

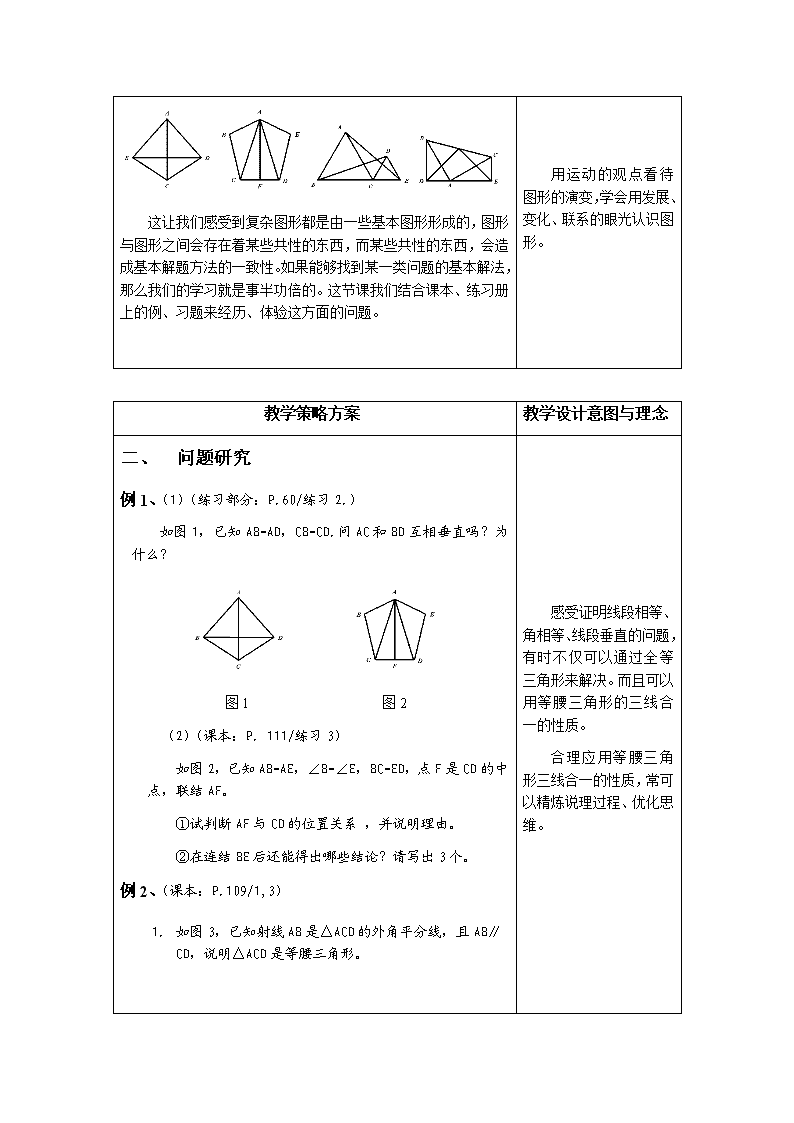
比较、归纳、提炼、升华 ——从教材例、习题谈《三角形》复习 一、教学目标 1、注重对教材中例、习题的解法和思路的复习，进一步提高认识，优化思维。 2、挖掘例、习题间的联系，学会把知识和技能纳入一定的系统，提高复习效率。 3、通过图形发散形式的演变，经历运动变化的过程，体验知识由“厚”到“薄” 的欣喜，从而培养善于比较归纳、乐于提炼升华的良好学习品质。 二、教学重点 1、巩固有关三角形的基础知识，优化思维过程。 2、提炼基本图形，学会举一反三、融会贯通，提高分析思维能力。 三、教学难点 正确辨析问题间的变化与联系，寻找问题解决的方法和规律。 四、教学过程 教学策略方案 教学设计意图与理念 一、 引入 进入全等三角形的学习以来，我们解决了不少问题，认识 了许多形形色色的图形。回头进行整理后发现，许多图形不是孤 立的，而是相互联系着的，它们可以看作是由一个三角形经过平 移、翻折、旋转得来。例如： A B C D E D E A C B B E D C A 而在这些图形的基础上，适当连结两点间的线段，则又可 以形成另外的图形。例如： D B C A F E D C B A D E A C B B E D C A 这让我们感受到复杂图形都是由一些基本图形形成的，图形 与图形之间会存在着某些共性的东西，而某些共性的东西，会造 成基本解题方法的一致性。如果能够找到某一类问题的基本解 法，那么我们的学习就是事半功倍的。这节课我们结合课本、练 习册上的例、习题来经历、体验这方面的问题。 用运动的观点看待 图形的演变，学会用发 展、变化、联系的眼光认 识图形。 教学策略方案 教学设计意图与理念 二、 问题研究 例 1、（1）（练习部分：P.60/练习 2.） 如图 1，已知 AB=AD，CB=CD.问 AC 和 BD 互相垂直吗？为 什么？ D B C A F E D C B A 图 1 图 2 （2）（课本：P. 111/练习 3） 如图 2，已知 AB=AE，∠B=∠E，BC=ED，点 F 是 CD 的中 点，联结 AF。 ①试判断 AF 与 CD 的位置关系 ，并说明理由。 ②在连结 BE 后还能得出哪些结论？请写出 3 个。 例 2、（课本：P.109/1,3） 1. 如图 3，已知射线 AB 是△ACD 的外角平分线，且 AB∥CD， 说明△ACD 是等腰三角形。 E D C B A 图 3 图 4 2. 如图 4，在△ABC 中，BD 平分∠ABC，过点 D 作 BC 的平 行线 DE，交 AB 于 E，说明 DE=BE 的理由。 思考：该两题在条件和结论上有什么共同之处？我们从中 可以提炼出什么结论？ 平行线 角平分线 其基本图形是： 3 2 1 E D CB A 2 1 E D B C A 图 5 图 6 感受证明线段相等、 角相等、线段垂直的问 题，有时不仅可以通过全 等三角形来解决。而且可 以用等腰三角形的三线 合一的性质。 合理应用等腰三角 形三线合一的性质，常可 以精炼说理过程、优化思 维。 复习常见问题，巩固 等角对等边的性质。 在图 5、6 中，“角 平分线、平行线、等腰三 角形”这三者中，若有两 条成立，则第三条必成 立．熟悉这个结论，对解 决包含该图形的较复杂 的题目是很有帮助的。 等腰三角形 教学策略方案 教学设计意图与理念 例 2 应用与拓展 在下列图形中，均给出了角平分线和平行线的条件，请指出 各图中的等腰三角形。由此，你还可以得出一些不同形式的结论 吗？ O E D C B A 图 7 例 3、（练习册：P.65/5；课本 P.103/2、3.） 5.如图 8,在△ABC 中,已知 AD⊥BC,垂足是点 D，AD=BD，DC=DE。 试说明∠C=∠1 的理由。 2. 如图 9,在△ABC 中,已知 AD⊥BC, 点 D 是垂足，CE=AB，∠1= ∠2，试说明 AD=DC 的理由。 3. 如图 10,在 Rt△ABC 中,已知∠ACB=900,CA=CB，CD=CE。试说 明 AD=BE 的理由。 1 E D C B A F E D C B A 2 1 A B E C F D 图 8 图 9 图 10 思考： 三道题在图形的结构上有什么共同特征？解决问题的途径 是什么？你发现三图中的 BE 或 CEF 或 BEF 与相应的 AC 或 AB 或 BD 有怎样的位置关系吗？ 三个图形都是由一个等腰直角三角形（或将证明是等腰三角 形）和一个直角三角形两个图形构成，而 BE 或 CEF 或 BEF 则是 从等腰直角三角形（或将证明是等腰三角形）的一个底角的顶点 过另一腰上的点引出的线段。 当三角形的内角平 分线（或外角平分线）和 平行于三角形的一边的 直线同时存在时，必定存 在一个等腰三角形。它可 以转移有关角和边的位 置，起到问题解决的桥梁 作用 这种多题一解规律 的掌握，对提高解题能力 也是十分有益的。 复习学生学习中常 感困难的问题，帮助学生 弄清知识间的联系，揭示 解决问题的一般方法。 教学策略方案 教学设计意图与理念 都是通过证明直角三角形与等腰三角形（或将证明是等腰三 角形）中的一直角三角形全等解决问题。 它们都是互相垂直的关系。 例 3 的应用与拓展 １．如图 11，正方形ＡＢＣＤ的边ＣＤ在正方形ＥＣＧＦ的边Ｃ Ｅ上，连结ＢＥ，ＤＧ，问线段ＢＥ与ＤＧ之间有怎样的关系？ 为什么？ G F E D B C A F E D B CA 图 11 图 12 2.如图 12，已知△ＡＢＣ中，∠Ａ＝９００， ∠ＡＢＣ＝４５０， ∠ＡＢＣ的平分线交ＡＣ于Ｄ，过Ｃ作ＢＤ的垂线交ＢＤ的延长 线于Ｆ．说明ＢＤ＝２ＣＥ的理由． 分析：在第一题中，如果连结 EG，可分解出图形 13，恰是 例 3 所研究的图形，从而解决问题的方式方法完全相同。这说明 条件背景虽然不同，但问题实质却是一样的。 在第二题中，若把图形绕点 F 逆时针旋转 900，则又转化成 例 3 所研究的图形，问题迎刃而解。 图 13 F E D C B A 2 1 三、 小结 1、 比较异同，发现联系。 2、 归纳共性，总结方法。 3、 提炼规律，举一反三。 4、 思想升华，能力提高。 四、 作业 １、如图 14，已知△ＡＢＣ和△ＣＤＥ都是等边三角形，ＡＤ边 上的高是ＣＦ，ＢＥ边上的高是ＣＥ． （１）说明ＣＦ＝ＣＨ的理由； （２）ＢＣ、ＣＤ不断变化时，ＥＢ与ＡＤ所成的角是否发生变 化，若不变，求出其夹角；若变化，则说明理由。 学习要善于比较、归 纳总结，不断研究方法上 的共性，引导学生举一反 三，触类旁通，努力实现 知识和能力的迁移。 把解题经验上升到理性 认识，会使学生感到贴 切，认识更深刻，掌握更 牢固，应用更灵活。 复习阶段的练习，如 果认为作一题多解的训 练是使学习内容由“薄” 到“厚”，那么，多题一 解则应是由“厚”到“薄” 的训练形式。 学习数学离不开解 题，但如果陷入茫茫的题 海中，“解题千万道，解 后抛九霄”，是难以达到 提高解题能力、发展思维 的目的的。善于做解题后 的小结，回顾解题过程， 总结解题经验和体会，再 进而作一题多解，一题多 问，一题多变，多题一解 的思考，挖掘题目的深度 和广度，扩大题目的辐射 面，这对提高解题能力是 十分重要的。 教学策略方案 教学设计意图与理念 O HF E D C B A 图 14 图 15 ２、两个全等的含３００、６００角的三角板ＡＤＥ和三角板ＡＢ Ｃ如图 15 所示放置，Ｅ、Ａ、Ｃ三点在一条直线上，连结ＢＤ， 取ＢＤ的中点Ｍ，连结ＭＥ、ＭＣ。试判断三角形ＥＭＣ的形状， 并说明理由。 说明：通过下列图形的演变，引出作业 1： E D C B A E D C B A E D C B A E D C B A E D C B A E D C B A E D C B A E C B A 上海市兴陇中学 李丽 2017-5-23 通过图形发散形式 的演变，逐步让学生学会 自觉掌握知识系统的方 法，使他们能把知识和技 能纳入一定的系统。 另一方面，知识系统 化，便于记忆和应用。心 理学中所说的记忆，就是 指建立联系，巩固练习。 工 作 单 例 2 应用与拓展 在下列图形中，均给出了角平分线和平行线的条件，请指出各图中的等腰三角形。由此， 你还可以得出一些不同形式的结论吗？ O E D C B A 例 3 的应用与拓展 １．如图 1，正方形ＡＢＣＤ的边ＣＤ在正方形ＥＣＧＦ的边ＣＥ上，连结ＢＥ，ＤＧ，问 线段ＢＥ与ＤＧ之间有怎样的关系？为什么？ G F E D B C A F E D B CA 图 1 图 2 2.如图 2，已知△ＡＢＣ中，∠Ａ＝９００， ∠ＡＢＣ＝４５０，∠ＡＢＣ的平分线交ＡＣ 于Ｄ，过Ｃ作ＢＤ的垂线交ＢＤ的延长线于Ｆ．说明ＢＤ＝２ＣＥ的理由． 作业： １、如图 3，已知△ＡＢＣ和△ＣＤＥ都是等边三角形，ＡＤ边上的高是ＣＦ，ＢＥ边上的 高是ＣＥ． （１）说明ＣＦ＝ＣＨ的理由； （２）ＢＣ、ＣＤ不断变化时，ＥＢ与ＡＤ所成的角是否发生变化，若不变，求出其夹角； 若变化，则说明理由。 O HF E D C B A 图 3 图 4 ２、两个全等的含３００、６００角的三角板ＡＤＥ和三角板ＡＢＣ如图 4 所示放置，Ｅ、Ａ、 Ｃ三点在一条直线上，连结ＢＤ，取ＢＤ的中点Ｍ，连结ＭＥ、ＭＣ。试判断三角形ＥＭＣ 的形状，并说明理由。