- 2021-11-11 发布 |
- 37.5 KB |
- 14页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考数学三轮真题集训冲刺知识点19二次函数代数方面的应用pdf含解析
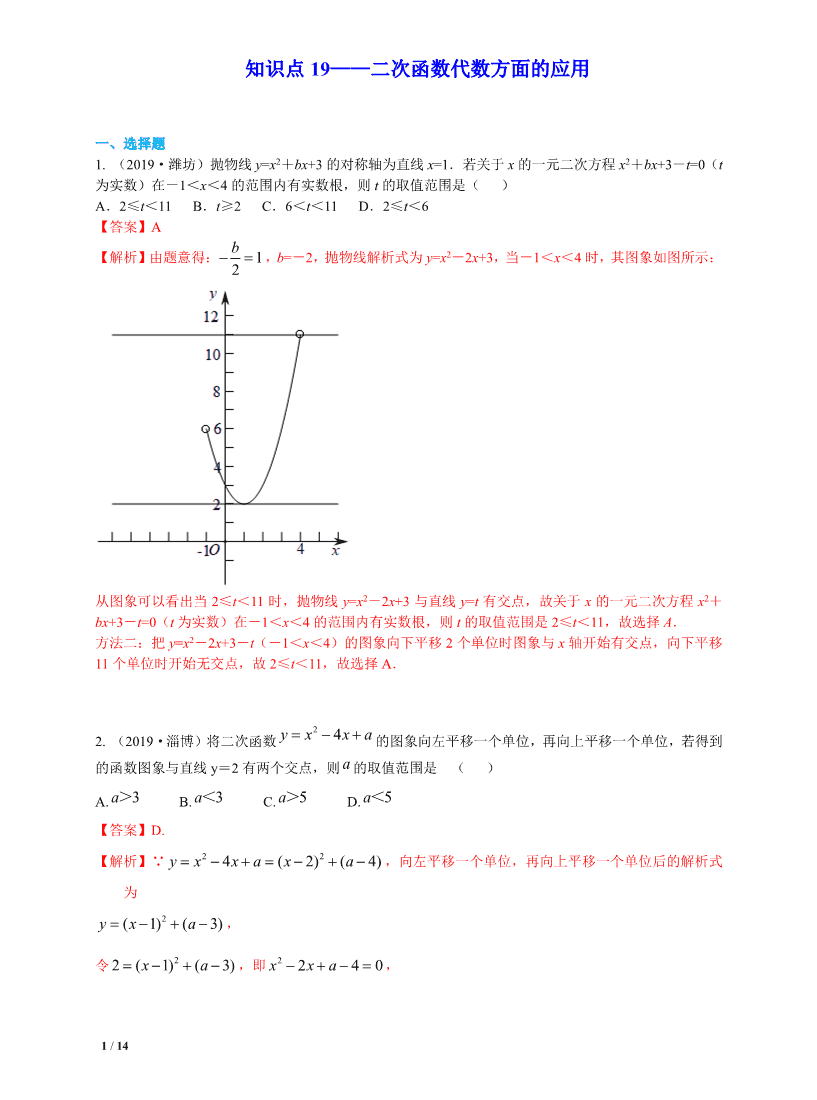
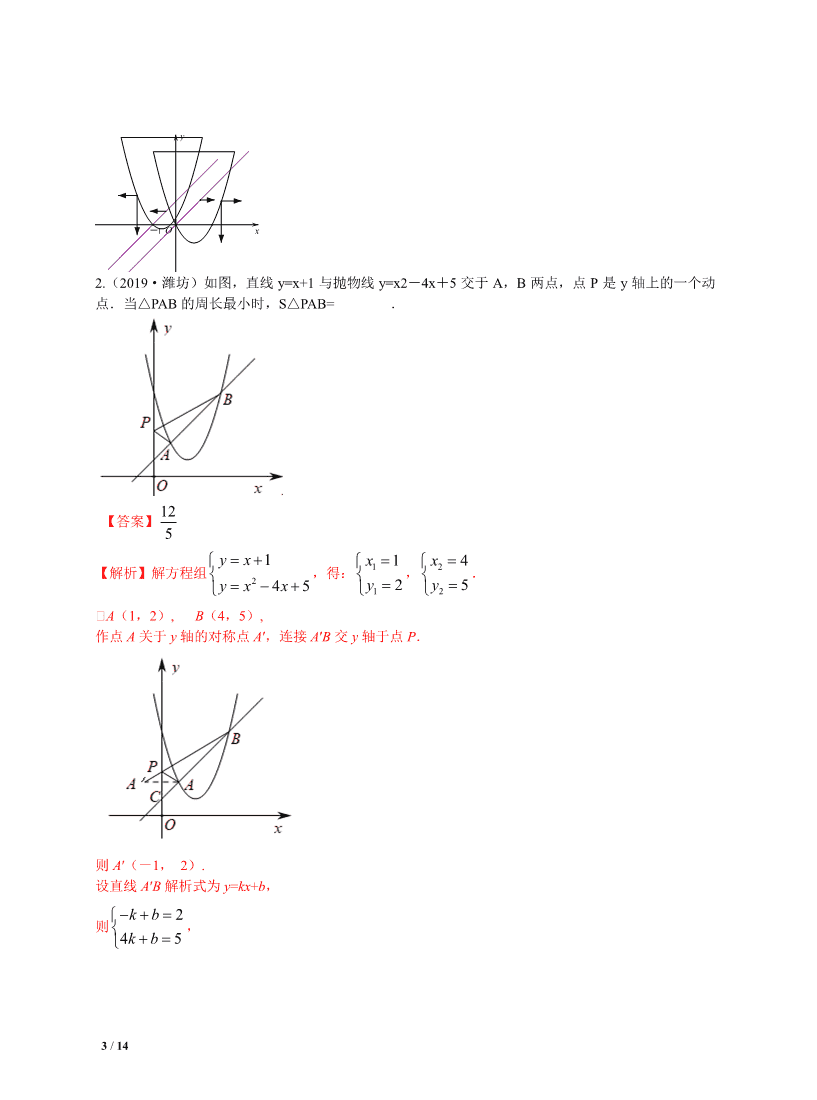
1 / 14 一、选择题 1. (2019·潍坊)抛物线 y=x2+bx+3 的对称轴为直线 x=1.若关于 x 的一元二次方程 x2+bx+3-t=0(t 为实数)在-1<x<4 的范围内有实数根,则 t 的取值范围是( ) A.2≤t<11 B.t≥2 C.6<t<11 D.2≤t<6 【答案】A 【解析】由题意得: 12 b−=,b=-2,抛物线解析式为 y=x2-2x+3,当 - 1<x<4 时,其图象如图所示: 从图象可以看出当 2≤t<11 时,抛物线 y=x2-2x+3 与直线 y=t 有交点,故关于 x 的一元二次方程 x2+ bx+3-t=0(t 为实数)在-1<x<4 的范围内有实数根,则 t 的取值范围是 2≤t<11,故选择 A. 方法二:把 y=x2-2x+3-t(-1<x<4)的图象向下平移 2 个单位时图象与 x 轴开始有交点,向下平移 11 个单位时开始无交点,故 2≤t<11,故选择 A. 2. (2019·淄博)将二次函数 2 4y x xa=−+的图象向左平移一个单位,再向上平移一个单位,若得到 的函数图象与直线 y=2 有两个交点,则 a 的取值范围是 ( ) A. 3a> B. 3a< C. 5a> D. 5a< 【答案】D. 【解析】∵ 224 ( 2) ( 4)y x xa x a= − += − + − ,向左平移一个单位,再向上平移一个单位后的解析式 为 2( 1) ( 3)yx a=− +−, 令 22 ( 1) ( 3)xa=− +−,即 2 2 40x xa− +−=, 知识点 19——二次函数代数方面的应用 2 / 14 由⊿ 4 4( 4) 0a=−−> ,得 5a< . 3. (2019·湖州)已知 a,b 是非零实数, ab> ,在同一平面直角坐标系中,二次函数 y1=ax2+bx 与一次函数 y2=ax+b 的大致图象不可能是( ) 【答案】D. 【解析】由 2 y ax b y ax bx = + = + ,解得 1 1 1x y ab = = + , 2 2 0 bx a y = − = ,故直线与抛物线的两个交点坐标分别为(1, a+b)和 (- b a ,0).对于 D 选项,从直线过第一、二、四象限可知:a<0,b>0.∵ ab> ,∴a+b<0.从而 (1,a+b)在第四象限,因此 D 选项不正确,故选 D. 二、填空题 1.(2019·安徽)在平面直角坐标系中,垂直于 x 轴的直线 l 分别与函数 y=x﹣a+1 和 y=x2﹣2a x 的 图 像相交于 P,Q 两点,若平移直线 l,可以使 P,Q 都在 x 轴的下方,则实数 a 的取值范围 是 . 【答案】a>1 或 a<-1 【解析】本题主要考查了一次函数图象及性质,二次函数图象及性质,平移的性质,以及数形结合,解 题的关键是结合题意,画出图象,利用数形结合分析问题. 本题问题的实质是自变量 x 在某个范围内, 两个函数的值都小于 0,即两个函数交点中较小的值小于 0.假设该两个函数的交点位于 x 轴上,则 x-a +1=0,x=a-1,代入二次函数的表达式中,得:(a-1)2-2a(a-1)=0,解得:a=1 或 a=-1. 当 a>1 时,随着 a 的变大,直线向右平移运动,抛物线向右、向下平移运算,如图,此时直线与抛物 线的最底交点位于第四象限;当 a<-1 时,随着|a|的变大,直线向左平移运动,抛物线向左、向下平移 运算,此时直线与抛物线的最底交点位于第三象限.综上所述,a 的取值范围为 a>1 或 a<-1. A. B. C. D. 3 / 14 2.(2019·潍坊)如图,直线 y=x+1 与抛物线 y=x2-4x+5 交于 A,B 两点,点 P 是 y 轴上的一个动 点.当△PAB 的周长最小时,S△PAB= . 【答案】12 5 【解析】解方程组 2 1 45 yx yx x = + =−+ ,得: 1 1 1 2 x y = = , 2 2 4 5 x y = = . �A(1,2), B(4,5), 作点 A 关于 y 轴的对称点 A′,连接 A′B 交 y 轴于点 P. 则 A′(-1, 2). 设直线 A′B 解析式为 y=kx+b, 则 2 45 kb kb −+ = += , x y -1 O 4 / 14 解得: 3,5 13 5 k b = = �直线 A′B: 3 13 55yx= + . ∴当△PAB 的周长最小时,点 P 的坐标为(0,13 5 ). 设直线 AB 与 y 轴的交点为 C,则 C(0,1) ∴S△PA B=S△PCB-S△PCA = 1 13 1 13( 1) 4 ( 1) 125 25 × −×−× −× =12 5 . 3.(2019·乐山)如图,点 P 是双曲线C : xy 4= ( 0>x )上的一点,过点 P 作 x 轴的垂线交直线 AB : 22 1 −= xy 于点Q ,连结OP ,OQ .当点 P 在曲线 C 上运动,且点 P 在Q 的上方时,△ POQ 面积的最大值是 . 【答案】3 【解析】∵点 P 是双曲线C : xy 4= ( 0>x )上的一点,∴可设点 P 坐标为(m, 4 m ), ∵ P Q ⊥ x 轴,Q 在 22 1 −= xy 图像上,∴Q 坐标为(m, 1 22 m − ), PQ= 4 m -( 1 22 m − ),∴△ POQ 面积 = 1 2 ×m×[ 4 m -( 1 22 m − ]= ( )21 234 m− −+,当 m=2 时,△ POQ 面积的最大值为 3. 三、解答题 1.(2019 浙江省杭州市,22,12 分)(本题满分 12 分) 5 / 14 设二次函数 y=(x-x1)(x-x2)( x1,x2 是实数) (1)甲求得当 x=0 时,y=0;当 x=1 时,y=0;乙求得当 x= 1 2 时,y=- 1 2 .若甲求得的结果都正确·你认 为乙求得的结果正确吗?说明理由. (2)写出二次函数图像的对称轴,并求该函数的最小值.(用含 x1,x2 的代数式表示). (3)已知二次函数的图象经过(0,m)和(1,n)两点(m,n 是实数),当 0<x1<x2<1 时. 求证: 0<mn< 1 16 . 【解题过程】(1)当 x=0 时,y=0;当 x=1 时,y=0;∴二次函数经过点(0,0),( 1,0), ∴x1=0,x2=1,∴y=x(x-1)=x2-x, 当 x= 时,y=- ,∴乙说点的不对; (2)对称轴为 x= ,当 x= 时,y=- 是函数的最小值; (3)二次函数的图象经过(0,m)和(1,n)两点,∴m=x1x2,n=1-x1-x2+x1x2, ∴mn=[- ][- ] ∵0<x1<x2<1,∴0≤- ≤ ,0≤- ≤ 1 4 , ∴0<mn< 1 16 . 2.(2019·淮安)如图,已知二次函数的图象与 x 轴交于 A、B 两点,D 为顶点,其中点 B 的坐标为 (5,0),点 D 的坐标为(1,3). (1)求该二次函数的表达式; (2)点 E 是线段 BD 上的一点,过点 E 作 x 轴的垂线,垂足为 F,且 ED=EF,求点 E 的坐标; (3)试问在该二次函数图像上是否存在点 G,使得△ADG 的面积是△BDG 的面积的 5 3 ?若存在,求出点 G 的坐标;若不存在,请说明理由. 第 2题图 第 2题备用图 【解题过程】解:(1)∵二次函数的顶点 D 的坐标为(1,3),且函数图象过点 B(5,0), 6 / 14 ∴设函数解析式为 3)1( 2 +−= xay ,则 03)15( 2 =+−a ,∴ 16 3−=a , ∴该二次的数的解析式为 3)1(16 3 2 +−−= xy ,即 16 25 8 3 16 3 2 ++−= xxy . (2)如图所示, 第 2题答图 1 ∵DC⊥x 轴,EF⊥x 轴, ∴△BEF∽△BDC, ∴ DC EF BD BE = , 设 EF=ED=m,则 35 5 mm =− , ∴m= 8 15 , ∴BF= 2 5 8 15 3 4 =× , 2 5 2 55 =−=OF , ∴E( 2 5 2 5, ) (3)根据题意知 A、B 两点直线 DG 的距离之比为 5:3,分两种情形: ①A、B 两点在直线 DG 的同旁,如图 2,则有 5 3= BM AN , 第 2题答图 2 7 / 14 由△HAN∽△HBN 得 BM AN BH AH = , ∴AH=12,∴H(-15,0), 又∵D 的坐标为(1,3). 设 DH 的解析式为:y=kx+b, 则 =+ =+− 3 015 bk bx ,解得 = = 16 45 16 3 b k , ∴DH 的解析式为 16 45 16 3 += xy . ∵点 G 为直线 DH 与抛物线 16 25 8 3 16 3 2 ++−= xxy 的另个交一个交点, ∴由 ++−= += 16 25 8 3 16 3 16 45 16 3 2 xxy xy 得 = = 16 45 0 y x 或 = = 3 1 y x , ∴G(0, 16 45 ). ②A、B 两点在直线 DG 的两旁,如图 3,则有 5 3= BM AN , 第 2题答图 3 ∵ 5 3= OB OA , ∴直线 DG 经过点 O,其解析为 y=3x. ∴由 ++−= = 16 25 8 3 16 3 3 2 xxy xy 得 −= −= 45 15 y x 或 = = 3 1 y x , ∴G(-15,-45). 8 / 14 综上所述,存在符合条件的点 G,其坐标为(0, 16 45 )或(-15,-45). 3.(2019·泰州) 已知一次函数 y1=kx+n(n<0)和反比例函数 y2=m x (m>0,x>0). (1)如图 1,若 n=-2,且函数 y1、y2 的图像都经过点 A(3,4). ①求 m、k 的值; ②直接写出当 y1>y2 时 x 的范围; (2)如图 2,过点 P(1,0)作 y 轴的平行线 l 与函数 y2 的图像相交于点 B,与反比例函数 y3=x n(x>0)的图像相交 于点 C. ①若 k=2,直线 l 与函数 y1 的图像相交于点 D.当点 B、C、D 中的一点到另外两点的距离相等时,求 m- n 的值; ②过点 B 作 x 轴的平行线与函数 y1 的图像相交于点 E.当 m-n 的值取不大于 1 的任意实数时,点 B、C 间的距离与点 B、E 间的距离之和 d 始终是一个定值.求此时 k 的值及定值. 第 3题图 【解题过程】(1)∵y2= m x (m>0,x>0),过点 A(3,4),∴4= 3 m ,∴m=12,∴反比例函数表达式为 y2= 12 x .又∵ 点 A(3,4)y1=kx+n 的图象上,且 n=-2,∴4=3k-2,∴k=2,所以一次函数表达式为 y1=2x-2. ②由图像可知,两个函数图象交点 A 的坐标为(3,4),所以当 x>3 时,y1>y2. (2)①因为 k=2,所以一次函数表达式为 y=2x+n,∵直线 l 过点 P(1,0),∴D(1,2+ n),B(1,m),C(1, n),又∵点 B、 C、D 中的一点到另外两点的距离相等,∴BD=BC 或 BD=DC 或 BC=CD,∴2+ n﹣m=m﹣n;或 m﹣(2+ n)=2+ n﹣n,或 m-n=n-(2+n),∴可得 m﹣n=1 或 m﹣n=4 或 m-n=-2; ②由题意可知,B(1,m),C(1, n),当 y1=m 时,kx+n=m,∴x= k nm − 即点 E 的横坐标为 k nm − ∴d=BC+BE = k nmnm −−+− 1 = 1)11)(( +−−m n k ,∵m-n 的值取不大于 1 的任意实数时, d 始终是一个定值,∴ 1− 1 k = 0 ,∴k=1,从而 d=1. 4.(2019·株洲)已知二次函数 y = ax2 + bx + c(a > 0) . (1)若 a=l,b=﹣2,c=﹣1.①求该二次函数图像的顶点坐标;②定义:对于二次函数 y = px2 + qx + r( p ≠ 0) ,满足方程 y = x 的 x 的值叫做该二次函数的“不动点”.求证:二次 9 / 14 函数 2y ax bx c= ++有两个不同的“不动点”. (2)设 b= 31 2 c ,如图所示,在平面直角坐标系 xOy 中,二次函数 2y ax bx c= ++的图像与 x 轴 分别相交于不同的两点 A( 1x ,0),B( 2x ,0),其中 1x <0, 2x >0,与 y 轴相交于点 C,连结 BC,点 D 在 y 轴的正半轴上,且 OC=OD,又点 E 的坐标为(1,0),过点 D 作垂直于 y 轴的 直线与直线 CE 相交于点 F,满足∠AFC=∠ABC.FA 的延长线与 BC 的延长线相交于点 P, 若 2 PC 5 PA 51a = + ,求该二次函数的表达式. 【解题过程】解:(1)①∵a=l,b=﹣2,c=﹣1 ∴y=x2-2x-1=(x-1)2-2 ∴顶点坐标为(1,-2); ②当 y=x 时,x=x2-2x-1, ∴x2-3x-1=0, ∴△=9+4=13>0 ∴有两个不相同的实数根,即有两个“不动点”。 (2) 10 / 14 ∵∠AFC=∠ABC,∠AEF=∠BEC, ∴△AEF∽△CEB, ∴ AE EF CE EB = , ∵DF∥OE,OC=OD, ∴OE 为△CDF 的中位线, ∵E(1,0), C(0,c); ∴CE= 21 C+ =EF ∵A(x1,0),B(x2,0), ∴AE=1-x1,BE=x2-1, ∴ 2 1 2 2 1- +1 11 x c xc = −+ ,∴1+c2=(1-x1)(x2-1)=x1+x2-x1x2-1, ∴ 2 2 b c bcc aa a ++=−− =− , ∵b= 31 2 c , ∴ 3 2 2 1 ( 2)22 2 cc ccc aa + ++=− =− ∴c=-2a. ∵∠AFC=∠ABC,∠P=∠P 11 / 14 ∴△PFC∽△PBA, ∴ PC CF PA AB = ∵ 2 PC 5 PA 51a = + ,CF=2CE,AB=x2-x1, ∴ 2 2 21 21 5 51 c xx a + =− + ∵ 2 21 4b acxx a −−= ,b= 31 2 c ,c=-2a., ∴a2=1, ∵a>0, ∴a=1. ∴b=-4,c=-2, ∴二次函数的表达式为 y=x2-4x-2 5.(2019 安徽)一次函数 y=kx+4 与二次函数 y=ax2+c 的图像的一个交点坐标为(1,2),另一个交点 是该二次函数图像的顶点. (1)求 k,a,c 的值; (2)过点 A(0,m)(0﹤m﹤4)且垂直于 y 轴的与二次函数 y=ax2+c 的图像相交于 B,C 两点,点 O 为坐标原点,记 W=OA2+BC2,求 W 关于 m 的函数解析式,并求 W 的最小值. 【解题过程】解:(1)因为点(1,2)在一次函数 y=kx+4 的图像上,所以 2=k+4,因为一 次函数 y=kx+4 与二次函数 y=ax2+c 图像的另一个交点是该二次函数图像的顶点,则(0,c) 在一次函数 y=kx+4 的图像上,即 c=4,又点(1,2)也在二次函数 y=ax2+c 的图像上,所 以 2=a+c,从而 a=﹣2; ………………6 分 (2)方法一:因为点 A 的坐标为(0,m)(0﹤m﹤4),过点 A 且垂直于 y 轴的直线与二次函数 y=﹣ 2x2+4 的图像交于点 B,C,所以可设点 B 的坐标为(x0,m),由对称性得点 C 的坐标为(﹣x0,m), 故 BC=2| x0 |,又点 B 在二次函数 y=﹣2x2+4 的图像上, 所以﹣2x02+4=m,即 x02=2﹣ 2 m ,从而 BC2=4 x02=8﹣2m,又 OA=m, 从而 W=OA2+BC2=m2﹣2m+8=(m﹣1)2+7(0﹤m﹤4),所以 m=1 时, W 有最小值 7. ………………12 分 6. (2019·台州)已知函数 y=x2+bx+c(b,c 为常数)的图象经过点(-2,4). (1)求 b,c 满足的关系式; (2)设该函数图象的顶点坐标是(m,n),当 b 的值变化时,求 n 关于 m 的函数解析式; (3)若该函数的图象不经过第三象限,当-5≤x≤1 时,函数的最大值与最小值之差为 16,求 b 的值. 解:(1)将点(-2,4)代入 y=x2+bx+c,得 4=(-2)2-2b+c,∴c=2b,∴b,c 满足的关系式是 c=2b. (2) 把 c=2b 代入 y=x2+bx+c,得 y=x2+bx+2b,∵顶点坐标是(m,n),n=m2+bm+2b,且 m=- 2 b ,即 b=-2m, ∴n= 12 / 14 (3) -m2-4m.∴n 关于 m 的函数解析式为 n=-m2-4m. (4) 由(2)的结论,画出函数 y=x2+bx+c 和函数 y=-x2-4x 的图象.∵函数 y=x2+bx+c 的图象不经过第三 象限, (5) ∴-4≤- 2 b ≤0.①当-4≤- 2 b ≤-2,即 4≤b≤8 时,如图 1 所示,x=1 时,函数取到最大值 y=1+3b,x =- 2 b 时,函数取到最小值 y= 28 4 bb− ,∴(1+3b)- 28 4 bb− =16,即 b2+4b-60=0,∴b1=6,b2=-10(舍去); ②当-2<- 2 b ≤0,即=≤b<4 时,如图 2 所示,x=-5 时,函数取到最大值 y=25-3b,x=- 2 b 时,函数取到 最小值 y= 28 4 bb− ,∴(25-3b)- 28 4 bb− =16,即 b2-20b+36=0,∴b1=2,b2=18(舍去);综上所述,b 的值为 2 或 6. 7.(2019·湖州)已知抛物线 y=2x2-4x+c 与 x 轴有两个不同的交点. (1)求 c 的取值范围; (2)若抛物线 y=2x2-4x+c 经过点 A(2,m)和点 B(3,n),试比较 m 和 n 的大小,并说明理由. 解:(1)∵抛物线 y=2x2-4x+c 与 x 轴有两个不同的交点, ∴方程 2x2-4x+c=0 有两个不相等的实数根. ∴△=(-4)2-4×2×c>0. ∴c<2 即为所求. (2)∵抛物线的对称轴为 x= 4 2 2 −− × =1,而 a=2>0, ∴在抛物线对称轴的右侧,y 随 x 的增大而增大. ∵2<3, ∴m<n. 8.(2019·凉山)已知二次函数 y=x2+x+a 的图象与 x 轴交于 A(x1,0)、B(x2,0)两点,且 22 12 11 xx + =1,求 a 的值. 解:对于抛物线y=x2+x+a,令y=0,∴x2+x+a =0,∵抛物线与x轴交于点A(x1,0),(x2,0), 13 / 14 ∴x1+x2=-1,x1x2=a,∵ 2 2 2 1 11 xx + = 2 2 2 1 2 2 2 1 xx xx + =1,∴x1 2+x2 2=x1 2x2 2,∴(x1+x2)2-2x1x2==x1 2x2 2,代入x1+x2=-1, x1x2=a,有:1-2a=a2,解得a=-1 2± ,∵方程有两个实数根,则△=1-4a>0,解得a< 4 1 ,∴a=-1- 2 . 9. (2019·巴中) 如图,一次函数 y1=k1x+b(k1,b 为常数,k1≠0)的图象与反比例函数 y2= 2k x (k2≠0,x>0) 的图象交于点 A(m,8)与点 B(4,2). ①求一次函数与反比例函数的解析式; ②根据图像说明,当 x 为何值时,k1x+b- 2k x <0. 解:①因为点 B(4,2)在反比例函数图象上,2= 2 4 k ,所以 k2=8,所以反比例函数解析式为 y2= 8 x (x>0),当 y =8 时,8= 8 x ,所以 x=1,所以点 A 坐标为(1,8),将 A(1,8),B(4,2)代入 y1=k1x+b,可得 1 1 8= 24 kb kb + = + ,所以 1 =2 10 k b - = ,一次函数解析式为 y1=-2x+10; ②k1x+b- k2 x <0,即 k1x+b< 2k x ,即 y1查看更多