2021年中考数学核心考点强化突破：函数与几何综合运用

2021年中考数学核心考点强化突破：函数与几何综合运用

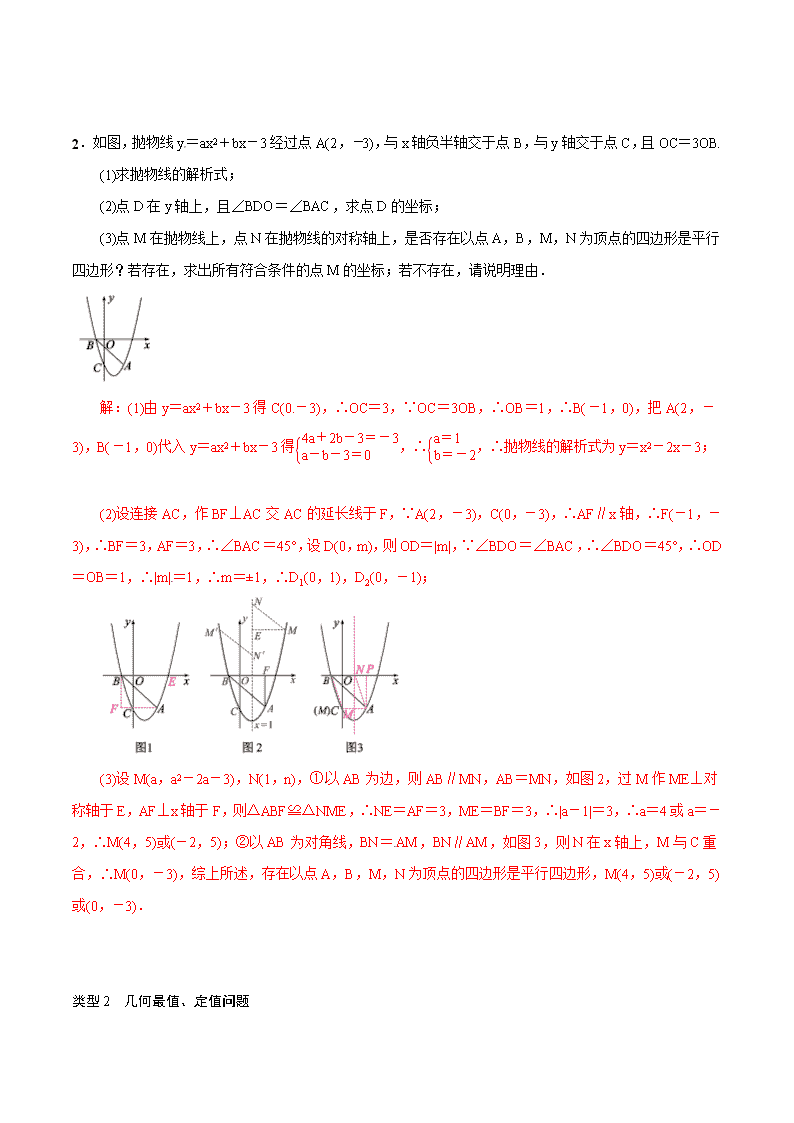
‎2021年中考数学核心考点强化突破：函数与几何综合运用 ‎ 类型1　存在性问题 存在性问题一般有以下题型：是否存在垂直、平行——位置关系；等腰、直角三角形、(特殊)平行四边形——形状关系；最大、最小值－－数量关系等．‎ ‎1．如图，已知二次函数y1＝－x2＋x＋c的图象与x轴的一个交点为A(4，0)，与y轴的交点为B，过A、B的直线为y2＝kx＋b.‎ ‎(1)求二次函数的解析式及点B的坐标；‎ ‎(2)由图象写出满足y1＜y2的自变量x的取值范围；‎ ‎(3)在两坐标轴上是否存在点P，使得△ABP是以AB为底边的等腰三角形？若存在，求出点P的坐标；若不存在，说明理由．‎ 解：(1)将A(4，0)代入y1＝－x2＋x＋c，得－42＋×4＋c＝0，解得c＝3.∴所求二次函数的解析式为y1＝－x2＋x＋3.∵当x＝0时，y1＝3，∴点B的坐标为(0，3)．‎ ‎(2)满足y1＜y2的自变量x的取值范围是：x＜0或x＞4.‎ ‎(3)存在，理由如下：作线段AB的中垂线l，垂足为C，交x轴于点P1，交y轴于点P2.∵A(4，0)，B(0，3)，∴OA＝4，OB＝3.∴在Rt△AOB中，AB＝＝5.∴AC＝BC＝.∵Rt△ACP1与Rt△AOB有公共∠OAB，∴Rt△ACP1∽Rt△AOB.∴＝，即＝，解得AP1＝.而OP1＝OA－AP1＝4－＝，∴点P1的坐标为(，0)．又∵Rt△P2CB与Rt△AOB有公共∠OBA，∴Rt△P2CB∽Rt△AOB.∴＝，即＝，解得P2B＝.而OP2＝P2B－OB＝－3＝，∴点P2的坐标为(0，－)．∴所求点P的坐标为(，0)或(0，－)．‎ ‎2．如图，抛物线y＝ax2＋bx－3经过点A(2，－3)，与x轴负半轴交于点B，与y轴交于点C，且OC＝3OB.‎ ‎(1)求抛物线的解析式；‎ ‎(2)点D在y轴上，且∠BDO＝∠BAC，求点D的坐标；‎ ‎(3)点M在抛物线上，点N在抛物线的对称轴上，是否存在以点A，B，M，N为顶点的四边形是平行四边形？若存在，求出所有符合条件的点M的坐标；若不存在，请说明理由．‎ 解：(1)由y＝ax2＋bx－3得C(0.－3)，∴OC＝3，∵OC＝3OB，∴OB＝1，∴B(－1，0)，把A(2，－3)，B(－1，0)代入y＝ax2＋bx－3得，∴，∴抛物线的解析式为y＝x2－2x－3；[来源:学_科_网Z_X_X_K]‎ ‎(2)设连接AC，作BF⊥AC交AC的延长线于F，∵A(2，－3)，C(0，－3)，∴AF∥x轴，∴F(－1，－3)，∴BF＝3，AF＝3，∴∠BAC＝45°，设D(0，m)，则OD＝|m|，∵∠BDO＝∠BAC，∴∠BDO＝45°，∴OD＝OB＝1，∴|m|＝1，∴m＝±1，∴D1(0，1)，D2(0，－1)；‎ ‎(3)设M(a，a2－2a－3)，N(1，n)，①以AB为边，则AB∥MN，AB＝MN，如图2，过M作ME⊥对称轴于E，AF⊥x轴于F，则△ABF≌△NME，∴NE＝AF＝3，ME＝BF＝3，∴|a－1|＝3，∴a＝4或a＝－2，∴M(4，5)或(－2，5)；②以AB为对角线，BN＝AM，BN∥AM，如图3，则N在x轴上，M与C重合，∴M(0，－3)，综上所述，存在以点A，B，M，N为顶点的四边形是平行四边形，M(4，5)或(－2，5)或(0，－3)．‎ 类型2　几何最值、定值问题 ‎3．如图，在平面直角坐标系中，平行四边形ABOC如图放置，将此平行四边形绕点O顺时针旋转90°得到平行四边形A′B′OC′.抛物线y＝－x2＋2x＋3经过点A、C、A′三点．‎ ‎(1)求A、A′、C三点的坐标；‎ ‎(2)求平行四边形ABOC和平行四边形A′B′OC′重叠部分的面积；‎ ‎(3)点M是第一象限内抛物线上的一动点，问点M在何处时，△AMA′的面积最大？最大面积是多少？并写出此时M的坐标．‎ 解：(1)当y＝0时，－x2＋2x＋3＝0，解得x1＝3，x2＝－1，∴C(－1，0)，A′(3，0)．当x＝0时，y＝3，∴A(0，3)．‎ ‎(2)设A′C′与OB相交于点D.∵C(－1，0)，A(0，3)，∴B(1，3)．∴OB＝＝.∴S△BOA＝×1×3＝.又∵平行四边形ABOC旋转90°得到平行四边形A′B′OC′，‎ ‎∴∠ACO＝∠OC′D.又∵∠ACO＝∠ABO，∴∠ABO＝∠OC′D.又∵∠C′OD＝∠AOB，∴△C′OD∽△BOA.∴＝()2＝()2.∴S△C′OD＝.‎ ‎(3)设M点的坐标为(m，－m2＋2m＋3)，连接OM.S△AMA′＝S△MOA′＋S△MOA－S△AOA′＝×3×(－m2＋2m＋3)＋×3×m－×3×3＝－m2＋m＝－(m－)2＋.(0＜m＜3)当m＝时，S△AMA′取到最大值，∴M(，)．‎ ‎ [来源:Zxxk.Com]‎ ‎4．如图，已知抛物线y＝ax2－2ax－9a与坐标轴交于A，B，C三点，其中C(0，3)，∠BAC的平分线AE交y轴于点D，交BC于点E，过点D的直线l与射线AC，AB分别交于点M，N.‎ ‎(1)直接写出a的值、点A的坐标及抛物线的对称轴；‎ ‎(2)点P为抛物线的对称轴上一动点，若△PAD为等腰三角形，求出点P的坐标；‎ ‎(3)证明：当直线l绕点D旋转时，＋均为定值，并求出该定值．‎ 解：(1)∵C(0，3)．∴－9a＝3，解得：a＝－.令y＝0得：ax2－2x－9a＝0，∵a≠0，∴x2－2x－9＝0，解得：x＝－或x＝3.∴点A的坐标为(－，0)，B(3，0)．∴抛物线的对称轴为x＝.‎ ‎(2)∵OA＝，OC＝3，∴tan∠CAO＝，∴∠CAO＝60°.∵AE为∠BAC的平分线，∴∠DAO＝30°.∴DO＝AO＝1.∴点D的坐标为(0，1)设点P的坐标为(，a)．‎ 依据两点间的距离公式可知：AD2＝4，AP2＝12＋a2，DP2＝3＋(a－1)2.当AD＝PA时，4＝12＋a2，方程无解．当AD＝DP时，4＝3＋(a－1)2，解得a＝2或a＝0，当a＝2时，点A，D，P三点共线，不能构成三角形，∴a≠2，∴点P的坐标为(，0)．当AP＝DP时，12＋a2＝3＋(a－1)2，解得a＝－4.∴点P的坐标为(，－4)．综上所述，点P的坐标为(，0)或(，－4)．‎ ‎(3)设直线AC的解析式为y＝mx＋3，将点A的坐标代入得：－m＋3＝0，解得：m＝，‎ ‎∴直线AC的解析式为y＝x＋3.设直线MN的解析式为y＝kx＋1.把y＝0代入y＝kx＋1得：kx＋1＝0，解得：x＝－，∴点N的坐标为(－，0)．∴AN＝－＋＝.将y＝x＋3与y＝kx＋1联立解得：x＝.∴点M的横坐标为.过点M作MG⊥x轴，垂足为G.则AG＝＋.∵∠MAG＝60°，∠AGM＝90°，∴AM＝2AG＝＋2＝.∴＋＝＋＝＝＝ 类型3　反比例函数与几何问题 ‎5．如图，P1，P2是反比例函数y＝(k＞0)在第一象限图象上的两点，点A1的坐标为(4，0)．若△P1OA1与△P2A1A2均为等腰直角三角形，其中点P1，P2为直角顶点．‎ ‎①求反比例函数的解析式．‎ ‎②(Ⅰ)求P2的坐标．‎ ‎(Ⅱ)根据图象直接写出在第一象限内当x满足什么条件时，经过点P1，P2的一次函数的函数值大于反比例函数y＝的函数值．‎ ‎[来源:Zxxk.Com]‎ 解：①过点P1作P1B⊥x轴，垂足为B，∵点A1的坐标为(4，0)，△P1OA1为等腰直角三角形，∴OB＝2，P1B＝OA1＝2，∴P1的坐标为(2，2)，将P1的坐标代入反比例函数y＝(k＞0)，得k＝2×2＝4，∴反比例函数的解析式为y＝；②(Ⅰ)过点P2作P2C⊥x轴，垂足为C∵△P2A1A2为等腰直角三角形，∴P2C＝A1C，设P2C＝A1C＝a，则P2的坐标为(4＋a，a)，将P2的坐标代入反比例函数的解析式y＝中，得a＝，解得a1＝2－2，a2＝－2－2(舍去)，∴P2的坐标为(2＋2，2－2)；‎ ‎(Ⅱ)在第一象限内，当2＜x＜2＋2时，一次函数的函数值大于反比例函数的函数值．‎ ‎6．如图，在平面直角坐标系中，正方形OABC的顶点O与坐标原点重合，点C的坐标为(0，3)，点A在x轴的负半轴上，点D，M分别在边AB，OA上，且AD＝2DB，AM＝2MO，一次函数y＝kx＋b的图象过点D和M，反比例函数y＝的图象经过点D，与BC的交点为N.[来源:学。科。网Z。X。X。K]‎ ‎(1)求反比例函数和一次函数的表达式；‎ ‎(2)若点P在直线DM上，且使△OPM的面积与四边形OMNC的面积相等，求点P的坐标．‎ ‎[来源:学*科*网Z*X*X*K]‎ 解：(1)∵正方形OABC的顶点C(0，3)，∴OA＝AB＝BC＝OC＝3，∠OAB＝∠B＝∠BCO＝90°，∵AD＝2DB，∴AD＝AB＝2，∴D(－3，2)，把D坐标代入y＝得：m＝－6，∴反比例函数解析式为y＝－，∵AM＝2MO，∴MO＝OA＝1，即M(－1，0)，把M与D的坐标代入y＝kx＋b中得：解得：k＝b＝－1，则直线DM解析式为y＝－x－1　(2)把y＝3代入y＝－得：x＝－2，∴N(－2，3)，即NC＝2，设P(x，y)，∵△OPM的面积与四边形OMNC的面积相等，∴(OM＋NC)·OC＝OM|y|，即|y|＝9，解得：y＝±9，当y＝9时，x＝－10，当y＝－9时，x＝8，则P坐标为(－10，9)或(8，－9)．‎