沪教版（上海）数学七年级第二学期-14 等腰三角形的性质

沪教版（上海）数学七年级第二学期-14 等腰三角形的性质

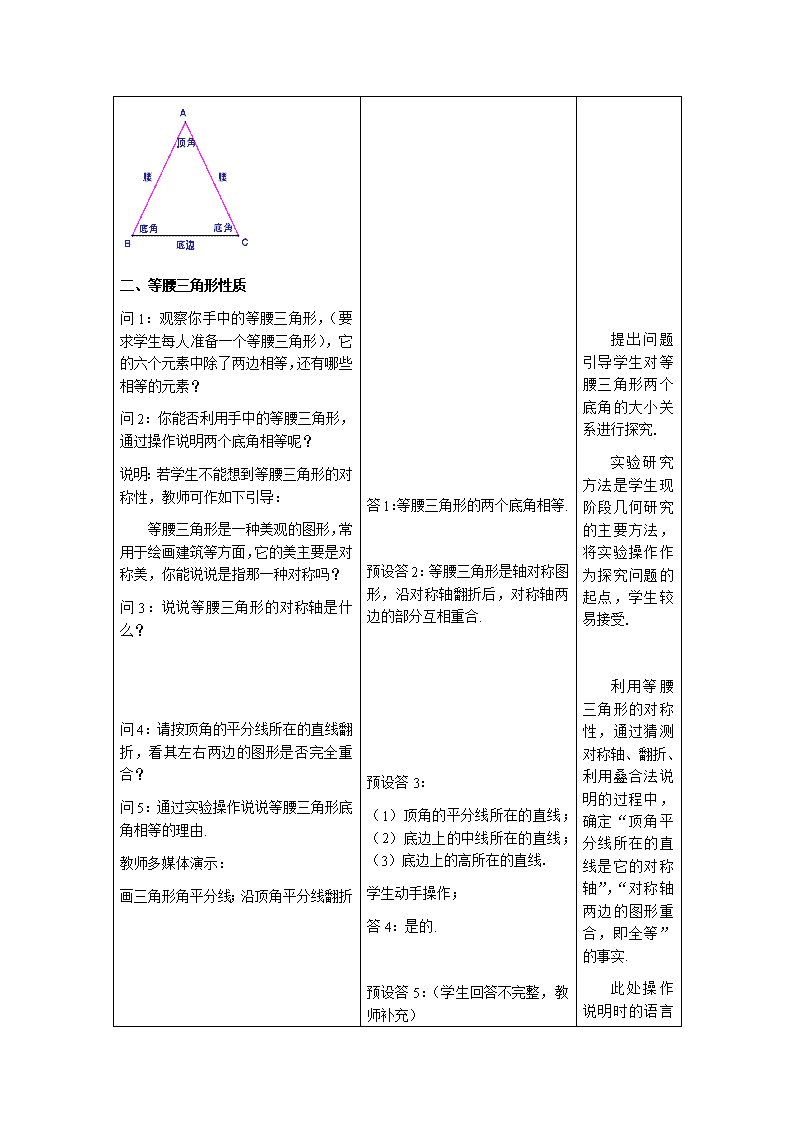
§14.5 等腰三角形的性质 教学目标： 1、 通过观察、操作、说理等活动，发现并归纳等腰三角形两个底角相等的性质，培养数学 语言归纳能力； 2、 经历用逻辑推理方法推导等腰三角形两个底角相等的性质的过程，体会实验归纳和逻辑 推理这两种研究方法的联系与区别； 3、 掌握等腰三角形两个底角相等及“三线合一”的性质，能运用等腰三角形的性质解决有 关的简单问题，发展基础性的逻辑推理能力. 教学重点：等腰三角形的性质的探究及应用 . 教学难点：等腰三角形“三线合一”性质的应用. 教学过程： 教师活动 学生活动 设计意图 一、 等腰三角形的相关概念 1、引入： 问 1：回顾三角形按边分类可以如何 分？ 这节课我们将主要研究等腰三角形的 性质. 出示课题：§14.5 等腰三角形的性质 2、等腰三角形的相关概念 问 2：什么是等腰三角形？ 说明：如图 ABC 是等腰三角形， AB=AC，这时，边 AB 和 AC 是它的腰， BC 是底边， A 是它的顶角， B 和 C 是底角. 二、等腰三角形性质 问 1：观察你手中的等腰三角形，（要 求学生每人准备一个等腰三角形），它 的六个元素中除了两边相等，还有哪些 答 1： ① 不等边三角形 三角形 ② 等腰三角形 等边三 角形 注：① 三边不相等 2 两条边相等 3 三边都相等 答 2：有两边相等的三角形叫做等 腰三角形. 答1：等腰三角形的两个底角相等. 由 已 学 的 三角形的分类 引出课题，体 现从一般到特 殊的研究问题 的方法. 提 出 问 题 引导学生对等 腰三角形两个 底角的大小关 系进行探究. ③ 相等的元素？ 问 2：你能否利用手中的等腰三角形， 通过操作说明两个底角相等呢？ 说明：若学生不能想到等腰三角形的对 称性，教师可作如下引导： 等腰三角形是一种美观的图形，常 用于绘画建筑等方面，它的美主要是对 称美，你能说说是指那一种对称吗？ 问 3：说说等腰三角形的对称轴是什 么？ 问 4：请按顶角的平分线所在的直线翻 折，看其左右两边的图形是否完全重 合？ 问 5：通过实验操作说说等腰三角形底 角相等的理由. 教师多媒体演示： 画三角形角平分线；沿顶角平分线翻折 C B A 小结： 通过操作我们发现： （1）等腰三角形是轴对称图形，顶角 平分线所在的直线是它的对称轴； （2）等腰三角形的两个底角相等. 问 6：如果不进行操作，你能否用几何 说理来说明等腰三角形的两个底角相 等呢？ 问题：已知 ABC 是等腰三角形，且 AB=AC，说明： CB  . C B A 2 1 C D B A 预设答 2：等腰三角形是轴对称图 形，沿对称轴翻折后，对称轴两 边的部分互相重合. 预设答 3： （1）顶角的平分线所在的直线； （2）底边上的中线所在的直线； （3）底边上的高所在的直线. 学生动手操作； 答 4：是的. 预设答 5：（学生回答不完整，教 师补充） （1）将 ABC 沿直线 AD 翻折， 因为 CADBAD  ，所以将 ABC 沿直线 AD 翻折后，射线 AB 与射线 AC 叠合. （2）由于 AB=AC，因此线段 AB 与线段 AC 重合，于是点 B 与点 C 重合，又因为点 D 与点 D 重合所 以线段 BD 与线段 CD 也重合，因 此 CB  . 答 6：学生口述： 解：过点 A 作 BAC 的平分线 AD，AD 与 BC 相交于点 D. AD 平分 BAC （已知），  21  （角的平分线的意 义）. 在 ABD 和 ACD 中，       ).(ADAD )(21 )( 公共边 ，已证 ，已知ACAB 实 验 研 究 方法是学生现 阶段几何研究 的主要方法， 将实验操作作 为探究问题的 起点，学生较 易接受. 利 用 等 腰 三角形的对称 性，通过猜测 对称轴、翻折、 利用叠合法说 明的过程中， 确定“顶角平 分线所在的直 线是它的对称 轴”，“对称轴 两边的图形重 合，即全等” 的事实. 此 处 操 作 说明时的语言 很重要，教学 中教师应引导 学生用规范的 语言叙述. 逻 辑 推 理 时所添加的辅 助线，是由“操 作”引出来的. 此 处 还 可 以用等腰三角 形底边上的中 线为辅助线， 推理得出等腰 三 角 形 的 性 质，有学生提 出给予肯定. 问 7：请归纳上面我们所得到的结论？ 如何用符号语言表示？ 小结：等腰三角形这一性质应用的前提 是：在同一个三角形中. 问 8：由上面的说理过程中还可以得到 哪些结论？ 问 9： ADCADB  说明 AD 与 BC 有怎样的位置关系？ 问 10：通过上述的说理，你还能得到 哪些结论？ 小结：等腰三角形的性质： 等腰三角形的顶角平分线、底边上 的中线、底边上的高互相重合（简称为 “等腰三角形的三线合一”）. 问 11：如何将这个性质用符号语言表 示呢？ 如图，如何表示 ○1 AD 为顶角的角 平 分 线 ？ ○2 AD 是 底 边 上 的 中 线 ？ ○3 AD 为底边上的高？ 2 1 C D B A 说明：“等腰三角形的三线合一”这一 性质指的是以上○1 、○2 、○3 中已知其中 任意一个就可以得出其余两个. 问 12：请用符号语言表是： 由○1 得○2 、○3  ABD ≌ )S.A.S(ACD  CB  （全等三角形的对 应角相等）. 答 7：（师生共同完成） 等腰三角形的一个性质： 等腰三角形的两个底角相等（简 称：“等边对等角”）. 在 ABC 中， ACAB  （已知）， CB  （等边对等角）. 答 8：  ABD ≌ )S.A.S(ACD  ADCADB  （全等三角 形的对应角相等）. BD=CD（全等三角形的对应边 相等）. 答 9： ADCADB  ， 且  180ADCADB ，  90ADCADB ， BCAD  . 答 10：AD 不仅是顶角的角平分 线，还是底边的中线和底边上的 高. 答 11： ○1 ∠1 =∠2； ○2 BD=CD； ○3 BCAD  . 将 所 得 性 质用符号语言 表述，提高符 号语言、文字 语言、图形语 言 的 转 化 能 力. 将 所 得 性 质用符号语言 表述，提高符 号语言、文字 语言、图形语 言 的 转 化 能 力. 等 腰 三 角 形的三线合一 性质的符号表 由○2 得○1 、○3 由○1 得○2 、○3 补充：有了这个性质，还可以进一步得 到：等腰三角形的对称轴还可认为是底 边上的高所在的直线，或底边上的中线 所在的直线.（大家前面的猜测是正确 的.） 三、等腰三角形性质的应用 我们通过探究得到了等腰三角形 的三个重要性质，它们如何应用呢？ 试一试： （1）如图，已知 AB=AC，  70B ， 求 C 和 A 的度数. C B A 问 1：题中有哪些条件？求什么? 问 2：如何求？依据是什么？ 教师根据学生回答板书： 解：（1）∵ ACAB  （已知）， ∴ CB  （等边对等角）， ∵  70B （已知）， ∴  70C （等量代换）. （2）∵  70CB ， 又  180CBA （三角 形内角和等于 180 ）， ∴  40A . 小结：在等腰三角形中若已知一个内 角，即可求出其它内角的大小. （2）已知 ABC 是等腰三角形，且有 一个内角为 70 ，那么其它两个内角的 答 12：（师生共同完成） （1）已知等腰三角形的顶角平分 线： 在三角形 ABC 中，AB=AC , ∵ AD 是角平分线 （已知）, ∴ BCAD  ，BD= CD（等腰 三角形的三线合一）. （2）已知等腰三角形底边上的中 线： 在三角形 ABC 中，AB=AC, ∵AD 是中线（已知） ∴ AD⊥BC ， ∠1 =∠2（等腰三 角形的三线合一） （3）已知等腰三角形底边上的 高： 在三角形 ABC 中，AB=AC, ∵AD 是高（已知） ∴ BD=CD， ∠1 =∠2（等腰三 角形的三线合一） 答 1：题中已知等腰三角形的底 角，求其另一底角和顶角的度数. 答 2：由等腰三角形“等边对等角” 的性质、三角形内角和性质求解. 示的第一种以 教 师 示 范 为 主，后面两种 以填空的形式 让学生练习. 变 式 是 “ 等 边 对 等 度数为_________________. 问：如何思考？ 小结：分类讨论的数学思想 （ 3 ） 如 图 ， 已 知 AB=AC ，  110BAC ，AD 是 ABC 的中线， 则 1 =_______， 2 =________； 2 1 C D B A 问：如何思考？ 小结：若已知等腰三角形及顶角平分 线、底边中线、底边上的高三线之一， 可考虑用“等腰三角形三线合一”的性 质来说明，而不用三角形的全等，以简 化说理过程. 课堂练习：P107，2、3. 补充例题：如图，已知 AB=AC，AD 是 BC 边 上 的 高 ， 且 ACDFABDE  , ，垂足分别是 E、F，试说明 BE=CF. 预设生答： 由于未告知已知角是顶角还是底 角，所以要分两种情况讨论： （1）当已知角为顶角，则另两角 为  5555 和 ； （2）当已知角为底角，则另两角 为  4070 和 . 答：  5555 和 或  4070 和 . 生答： 预 设 1 ， 利 用 已 知 条 件 说 明 ABD 和 ACD 全等，从而得出 所求结论. 预设 2， 本题已知等腰三角形顶角，及底 边上的中线，可考虑用“等腰三 角形三线合一”的性质求解. ∵ ACAB  （已知）， 又∵AD 是 ABC 的中线（已 知） ∴ BAC 2 121 （等 腰三角形三线合一）， ∵  110BAC （已知）， ∴  5521 （等式性质）. 角”性质的应 用，同时渗透 分类讨论的思 想. （3）为课 本例题 2，是 “等腰三角形 三线合一”这 一性质的简单 应用，此处改 为填空题，有 学生习惯用三 角形的全等说 明问题，应引 导学生学会使 用简捷方法解 决问题. 补 充 例 题 可用三角形的 全等来说明， 但比较繁琐， 引导学生灵活 运用等腰三角 形 的 性 质 解 问：如何说明 BE=CF？ 问：如何说明 CDFBDE  ？ 教师根据学生回答板书： 解：∵AB=AC， ∴ CB  （等边对等角）， ∵AD 是 BC 边上的高（已知）， ∴BD=CD （等腰三角形三线合一）， ∵ ACDFABDE  , （已知）， ∴  9021 （垂直的意义）， 在 CDFBDE  和 中：       , , ,21 CDBD CB ∴ BDE ≌ CDF （A.A.S）. ∴BE=CF（全等三角形的对应边相 等）. 补充练习: 如图，四边形 ABCD 的对角线 AC 与 BD 相交于点 O，AB=AD，且 BDAC  ， 试说明 21  . 四、课堂练习 A 组： 1. （1）将“等腰三角形的顶角平分 线平分并且垂直于底边”.在△ABC 中，如果 AB=AC，∠1=∠2，那么 答：可先说明 CDFBDE  ； 答：由 ACDFABDE  , ，可 得 21  ； 由于 AB=AC，由“等边对成角” 可得： CB  ； 又因为 AD 是高，由“等腰三角形 三线合一”的性质可得：BD=CD. 所以， BDE ≌ CDF （A.A.S） 答案： 1（1）BD=DC,AD⊥BC. 题，优化解题 过程. 此 题 还 可 同 过 说 明 AED 和 AFD 全等， 说明 AE=AF， 从 而 得 到 BE=CF. 巩固“等腰三角 形的三线合一” 性 质 . 并 熟 练 ______=______，且_____. （2）“等腰三角形底边上的中线垂 直于底边，并且平分顶角”，在△ABC 中，如果 AB=AC，____，那么_____， 且_____. （3）“等腰三角形底边上的高平分 底边和顶角”.在△ABC 中，如果 AB=AC， ____，那么_____，且_____. 2. 如图，已知 AB=AC，AD=AE，说明 DE∥BC 的理由. B 组： 小明练习册上的一个等腰三角形被墨 迹污染了，只有它的底边 AB 和∠B 还 保留着，请你画出练习册上原来的等腰 三角形形状. （2）BD=DC, AD⊥BC, ∠1=∠2. （3）AD⊥BC，BD=DC, ∠1=∠2. 理由： ∵AB=AC(已知)， ∴∠B=∠C(等边对等角). 又∵∠A+∠B+∠C=180°（三角形 内角和等于 180°）， ∴∠A+2∠B=180°(等量代换). 得∠B= 2 1 （180°-∠A）（等式性 质）. 同理得 ∠1= 2 1 （180°-∠A）. ∴∠1=∠B. ∴DE∥BC（同位角相等，两直线 平行）. 方法一：画出∠A，使∠A=∠B， ∠A 和∠B 另一边的交点 C 就是等 腰三角形的顶角的顶点. 掌握其几何符 号 语 言 的 表 达. “ 等 边 对 等 角”和“三角 形内角和等于 180°”及平行 线判定的综合 运 用 . 利 用 所 学知识进行简 单说理，发展 基础性的逻辑 推理能力. 此题作法一， 为下节等腰三 角形判定作铺 垫. 作法二，利用 到等腰三角形 的对称性. 五、课堂小结 今天你主要学习了什么，有什么收 获？ 六、布置作业 练习册，习题 14.5 方法二：画出线段 AB 的垂直平分 线，与∠B 的另一边的交点 C 就是 等腰三角形的顶角的顶点. 预设生答： 等腰三角形的三条性质及其应 用. 课后作业 试 题 解 答 设计意图 A 组： 1.填空： （1）如果等腰三角形的一个底角为 34°，那么另外两个角的度数分别为 _____、______. （2）如果等腰三角形的底边和一腰长 分别为 12cn、15cm，那么这个三角形 的周长为_______cm.. （3）如果等腰三角形的两边长分别为 12cm、8cm，那么这个三角形的周长为 ______cm.(练习册 p54/1) 答案： (1)34°，112°. (2)42cm. (3) 42cm 或 28cm.(注意等腰三角形的 两边长分别为 12cm、8cm，没说哪一 个是腰,哪一个是底,因此要分类讨论, 两种情况) . 等 腰三 角 形 意义 及 两 底角 相 等 的 运 用 ，注 意 （3）题的 分 类讨 论 思 想， 以 及 利用 三 角 形三 边 关 系定 理 确 定三 角 形 是否 存 在 . 注 意 双 解题 目 学 生易 漏 解出错. 2. 如 图 ， 已 知 点 D 在 BC 上 ， AB=AC=BD，AD=DC. （1）图中等腰三角形共有____个. （2）∠BDA 是∠C 的几倍？ （3）∠BAD 是∠C 的几倍？ （4）求∠C 的度数. (练习册 p55/2) 解：（2）在△ADC 中， 因为 AD=DC（已知）, 所以_____=_____（ ）. 因为∠BDA=∠DAC+______（ ）, 所以∠BDA=_____∠C. （3）在△ABD 中， 因为 AB=BD（已知）, 所以______=______（ ）. 所以∠BAD=______∠C. （4）在△ABC 中， 因为 AB=AC（已知）, 所以______=______（ ）. 又 因 为 ∠ B+ ∠ BDA ∠ BAD=____ ° （ ）, 所以______∠C=______°. 所以∠C=______°. 答案： （1） 三个. （2）在△ADC 中， 因为 AD=DC（已知）, 所以∠C =∠DAC （等边对等角 ）. 因为∠BDA=∠DAC+∠C（ 三角形的 一个外角等于和它不相邻的两个内角 的和）. 因为∠BDA= 2 ∠C. （3）在△ABD 中， 因为 AB=BD（已知）, 所以 ∠BAD = ∠BDA （等边对等 角 ）. 所以∠BAD= 2 ∠C. （4）在△ABC 中， 因为 AB=AC（已知）, 所以 ∠B = ∠C （等边对等角 ）. 又因为∠B+∠BDA+∠BAD= 180° （三角形内角和等于 180°）， 所以 5 ∠C= 180°. 所以∠C= 36°. “ 等 边 对 等角” 和 三角 形 内 角和 及 外 角性 质 的 综合 运 用 . 强 调 “等 边对 等 角”的 应 用 方 法 . 通 过 填 空和 说 理 ，发 展 学 生基 础 性 的逻 辑 推 理 能 力. 3.如图，已知 AB=AC，BD=CD， ∠B=30°，求∠BAD 的度数. (练习册 p55/3) 解：在△ABC 中，AB=AC（已知）， 因为 BD=CD（已知）， 所以 AD⊥BC（ ） . 得∠ADB=90°（ ）. 又因为_____________=180° （ ） 所以∠BAD=180°-∠ADB-∠B. 因为∠B=30°（已知）, 解：在△ABC 中，AB=AC（已知）， 因为 BD=CD（已知）， 所以 AD⊥BC（ 等腰三角形的三线合 一） . 得∠ADB=90°（垂直的意义）. 又因为 ∠B+∠BDA+∠BAD = 180° （三角形内角和等于 180°）， 所以∠BAD=180°-∠ADB-∠B. 因为∠B=30°（已知）, 所以∠BAD= 60°. “等 腰 三角 形 的 三线 合 一” 和“三 角 形内 角 和 等 于 180°”综 合 运用 ， 特 别强 调 “等腰三角 形 的三 线 合一”的运 用 . 通 过 填 空及 说 理 学会 写 说 理 过 所以∠BAD=_______. 程. B 组： 1.如图，已知 AD∥BC，BD=CD, ∠A=120°，∠ABD=30°. (1) 求∠DBC 的度数. （2）求∠BDC 的度数. (练习册 p55/4) 解：（1）∵AD∥BC(已知)， ∴∠A+∠ABC=180°（两直线平行，同 旁内角相等）. ∵∠A=120°（已知）， ∴∠ABC=60°（等式性质）. ∵∠1=30°（已知）， ∴∠2=∠ABC -∠1 =60°-30°= 30° （等式性质）. （2）∵BD=CD（已知）, ∴∠2=∠C（等边对等角 ）. ∵∠2= 30°（已知）, ∴∠C= 30°（等量代换）. ∵∠2+∠BDC+∠C = 180°（三角形内 角和等于 180°）， ∴∠BDC=180°- 30°- 30° =120°（等式性质）. “等 边对 等 角”和 “三 角形 内 角和 等 于 180°” 及 平行 线 性 质的 综 合 运 用 . 特 别强 调 “等 边对 等 角”的 运 用 . 利 用 所学 知 识 进行 简 单 说理 ， 发 展基 础 性 的逻 辑 推 理 能 力. 2.如图，在△ABC 中，AB=AC，BD 为边 AC 上的高，试探究∠CBD 与 ∠A 之间有什么数量关系？(练习册 p56/5) （1） 用量角器量出∠CBD 和∠A 的 大小. （2） 再画两个形状、大小不同的等 腰三角形 ABC，其中 AB=AC， BD 为边 AC 上的高，用量角器 分别量出∠CBD 和∠A 的大 小. （3） 根据上面三组数据，猜想∠ CBD 与∠A 之间的数量关系， 并对猜想结果进行说明. 解：（1）∠CBD=25°, ∠A=50°. （2）根据所画图形测量. （3）∠CBD = 2 1 ∠A. 理由： 方法一： ∵BD 为边 AC 上的高（已知）， ∴∠BDC=90°（三角形高的意义）. ∵∠1+∠BDC+∠C = 180°（三角形内 角和等于 180°）， ∴∠1=90°-∠C（等式性质）. ∵AB=AC（已知）， ∴∠ABC=∠C（等边对等角 ）. ∵∠A+∠ABC+∠C = 180°（三角形内 角和等于 180°）， ∴∠A+2∠C = 180°（等量代换）. ∴∠C = 90°- 2 1 ∠A（等式性质）. ∴∠1= 2 1 ∠A（等量代换）. （ 1 ） （2）进行 试 验 操 作 ，猜 想 结 论 . 再 通过（3） 进 行说 理 此 结论 正 确 . 注 意 又 特殊 到 一 般的 研 究 问题 的 方法. （ 3 ） 中 “等 边对 等 角”和 “三 角形 内 角和 等 于 180°” 的 运 用 . 利 用所 学 知 识进 行 简 单 说 方法二： 过点 A 作 AE⊥BC,垂足为 E， ∵AB=AC(已知)， ∴∠2= 2 1 ∠BAC（等腰三角形的三线合 一）. ∠AEC=90°（垂直的意义） ∵∠2+∠AEC+∠C = 180°（三角形内 角和等于 180°）， ∴∠2=90°-∠C（等式性质）. ∵BD 为边 AC 上的高（已知）， ∴∠BDC=90°（三角形高的意义）. ∵∠1+∠BDC+∠C = 180°（三角形内 角和等于 180°）， ∴∠1=90°-∠C（等式性质）. ∴∠1=∠2（等量代换）. ∴∠2= 2 1 ∠BAC（等量代换）. 理 ，训 练 学 生逻 辑 推 理 能 力.