沪科版九年级数学上册：期末复习培优集训2

沪科版九年级数学上册：期末复习培优集训2

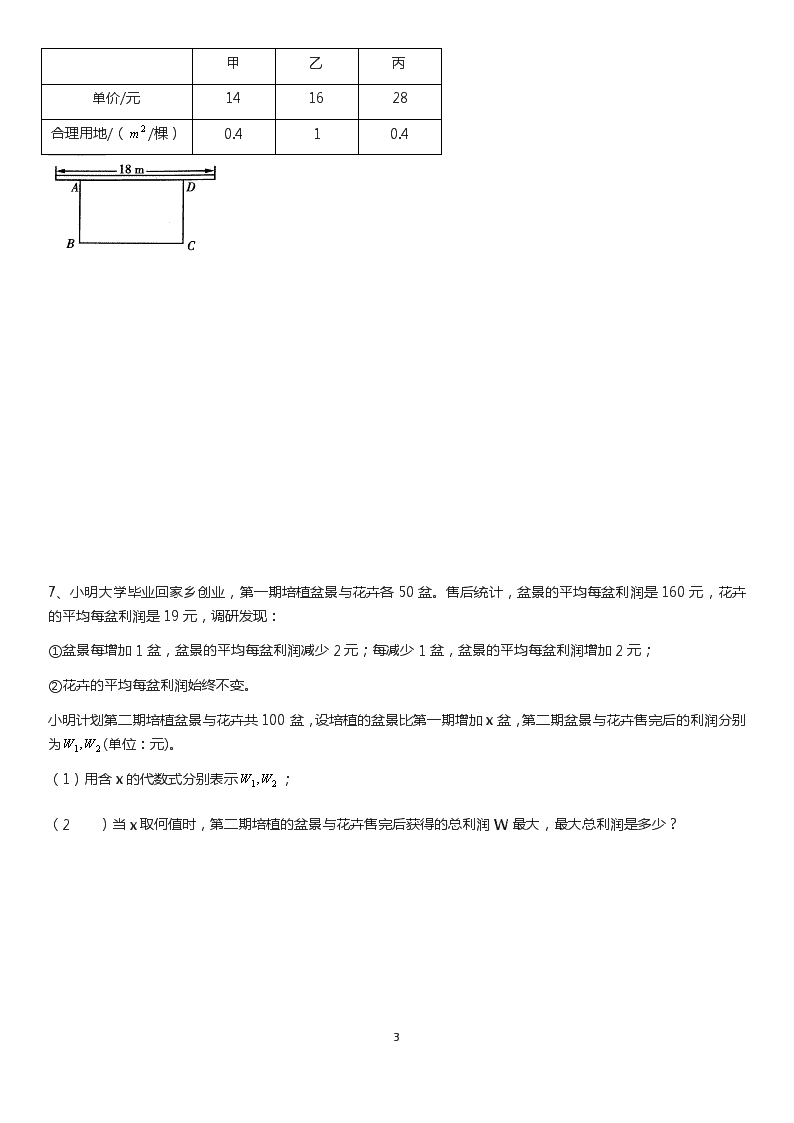
1 二次函数的应用 命题点 1 二次函数的实际应用 1、如图(1)，北中环桥是山西太原的一座跨汾河大桥，它有五个抛物线型钢拱，钢拱通过吊杆、拉索与主梁相连。 最高的钢拱(可近似看成抛物线的一部分)在同一竖直平面内，与拱脚所在的水平面相交于 A、B 两点。拱商为 7 米(即 最高点 O 到 AB 的距离为 78 米)，跨径为 90 米(即 AB=90 米)，以最高点 0 为坐标原点，以平行于 AB 的直线为 x 轴建立平面直角坐标系如图(2)所示，则此钢拱所在的抛物线的函数表达式为（ ） A. 2 675 26 xy  B. 2 675 26 xy  C. 2 1350 13 xy  D. 2 1350 13 xy  2、从地面竖直向上抛出一小球，小球的高度 h(单位:m)与小球的运动时间 t(单位:s)之间的函数关系如图所示。 给出下列结论:①小球在空中经过的路程是 40m；②小球抛出 3s 后，速度越来越快；③小球抛出 3s 时速度为 0； ④小球的高度 h=30m 时，t=1.5s。其中正确的是（ ） A.①④ B.①② C.②③④ D.②③ 3、如图，若被击打的小球飞行高度 h(单位:m)与飞行时间 t(单位:s)之间具有的关系为 2520 tth  ，则小球从飞出 到落地所用的时间为_________。 4、扶贫工作小组对果农进行精准扶贫，帮助果农将一种有机生态水果拓宽了市场。与去年相比，今年这种水果的 产量增加了 1000 千克，每千克的平均批发价比去年降低了 1 元，批发销售总额比去年增加了 20%。已知去年这种 水果批发销售总额为 10 万元。 （1）求今年这种水果每千克的平均批发价是多少元？ （2）某水果店今年从果农处直接批发，专营这种水果。调查发现，若每千克的平均销售价为 41 元，则每天可售出 300 千克；若每千克的平均销售价每降低 3 元，每天可多卖出 180 千克。设水果店一天的利润为 w 元，当每千克 的平均销售价为多少元时，该水果店一天的利润最大，最大利润是多少？（计算利润时，其他费用忽略不计） 2 5、某商店销售一种商品，经市场调查发现，该商品的周销售量 y(件)是售价 x(元/件)的一次函数。其售价、周销售 量、周销售利润 w(元)的三组对应值如下表： 售价 x/（元/件） 50 60 80 周销售量 y/件 100 80 40 周销售利润 w/元 1000 1600 1600 注：周销售利润=周销售量×（售价-进价） （1）①求 y 关于 x 的函数解析式(不要写出自变量的取值范围)； ②该商品进价是________元/件，当售价是_______元/件时，周销售利润最大，最大利润是__________元。 （2）由于某种原因，该商品进价提高了 m 元/件(m>0)，物价部门规定该商品售价不得超过 65 元/件。该商店在 今后的销售中，周销售量与售价仍然满足(1)中的函数关系，若周销售最大利润是 1400 元，求 m 的值。 6、为响应荆州市“创建全国文明城市”的号召，某单位不断美化环境，拟在一块矩形空地上修建绿色植物园，其 中一边靠墙，可利用的墙长不超过 18m，另外三边由 36m 长的棚栏围成，设矩形 ABCD 空地中，垂直于墙的边 AB=x m，面积为 y 2m (如图)。 （1）求 y 与 x 之间的函数关系式，并写出自变量 x 的取值范围； （2）若矩形空地的面积为 160 2m ，求 x 的值； （3）若该单位用 8600 元购买了甲、乙、丙三种绿色植物共 400 棵(每种植物的单价和每棵栽种的合理用地面积如 下表)，则丙种植物最多可以购买多少棵？此时，这批植物可以全部栽种到这块空地上吗？请说明理由。 甲 乙 丙 单价/元 14 16 28 合理用地/（ 2m /棵） 0.4 1 0.4 3 7、小明大学毕业回家乡创业，第一期培植盆景与花卉各 50 盆。售后统计，盆景的平均每盆利润是 160 元，花卉 的平均每盆利润是 19 元，调研发现： ①盆景每增加 1 盆，盆景的平均每盆利润减少 2 元；每减少 1 盆，盆景的平均每盆利润增加 2 元； ②花卉的平均每盆利润始终不变。 小明计划第二期培植盆景与花卉共 100 盆，设培植的盆景比第一期增加 x 盆，第二期盆景与花卉售完后的利润分别 为 21,WW (单位：元)。 （1）用含 x 的代数式分别表示 21,WW ； （2 ）当 x 取何值时，第二期培植的盆景与花卉售完后获得的总利润 W 最大，最大总利润是多少？ 8、某超市拟于中秋节前 50 天里销售某品牌的月饼，其进价为 18 元/kg。设第 x 天的销售价格为 y 元/kg，销售量 为 m kg。该超市根据以往的销售经验得出以下的销售规律：①当 1≤x≤30 时，y=40；当 31≤x≤50 时，y 与 x 满 足一次函数关系，且当 x=36 时，y=37；x=44 时，y=33。②m 与 x 之间的函数关系式为 m=5x+50。 （1）当 31≤x≤50 时，y 与 x 之间的函数关系式为_______________； （2）当 x 为多少时，当天的销售利润 W(元)最大，最大利润为多少？ （3）该超市希望第 31 天到第 35 天的日销售利润 W 随 x 的增大而增大，则需要在当天销售价格的基础上涨 a 元 /kg，求 a 的最小值。 4 命题点 2 二次函数与其他知识的综合应用 9、已知一次函数 4 kxy 与二次函数 caxy  2 的图象的一个交点坐标为(1,2)，另一个交点是该二次函数图象的 顶点。 （1）求 k、a、c 的值； （2）过点 A(0,m)(0

查看更多