江苏省宜兴外国语学校2020－2021学年九年级数学第一学期期中考试复习卷

江苏省宜兴外国语学校2020－2021学年九年级数学第一学期期中考试复习卷

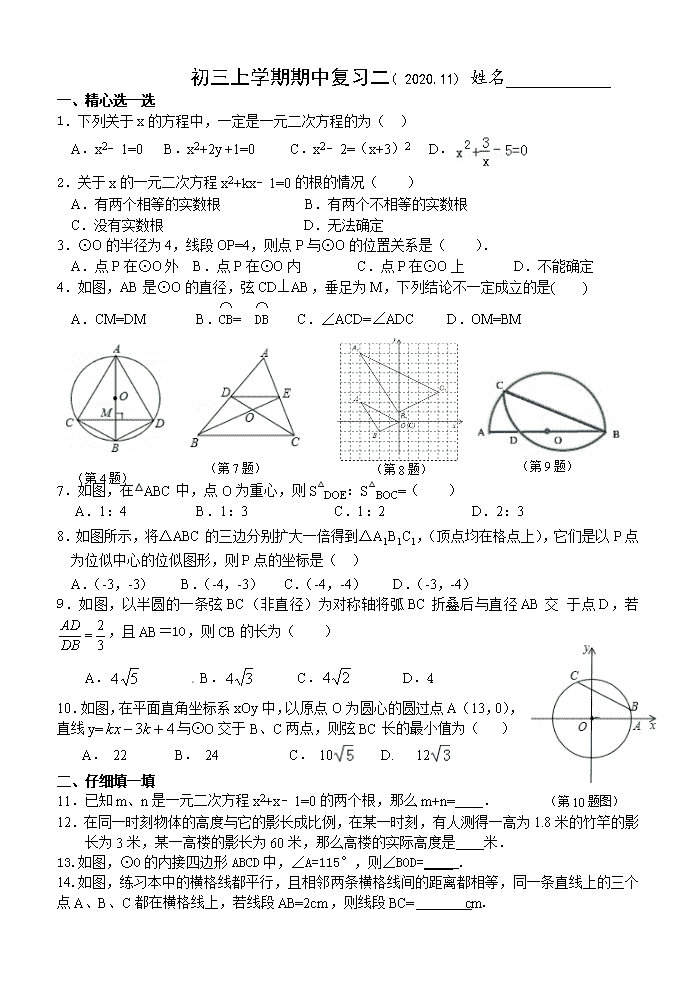
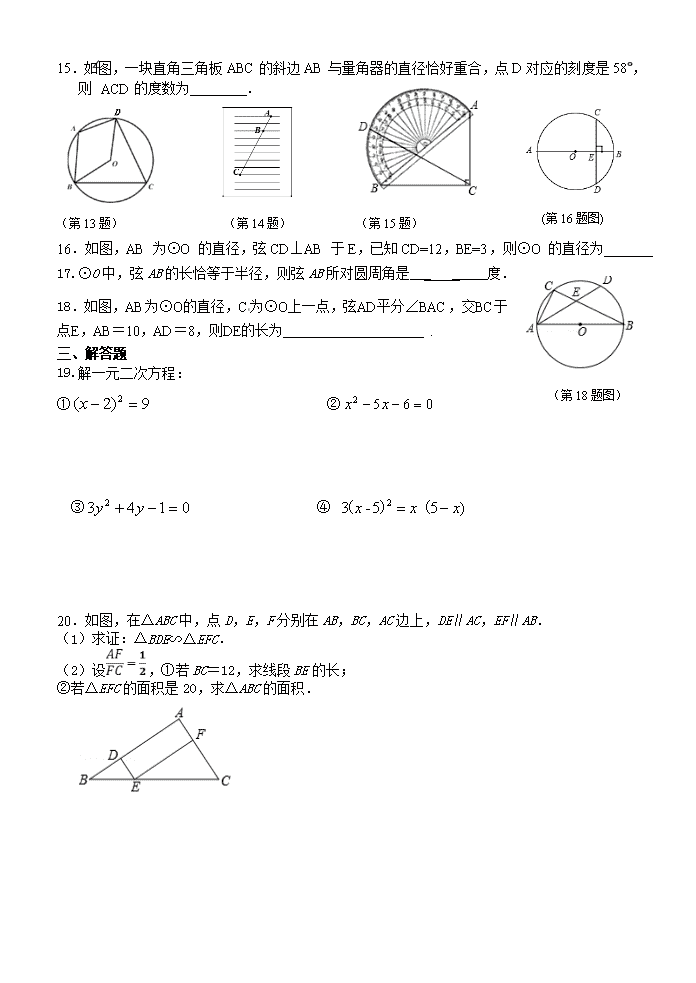
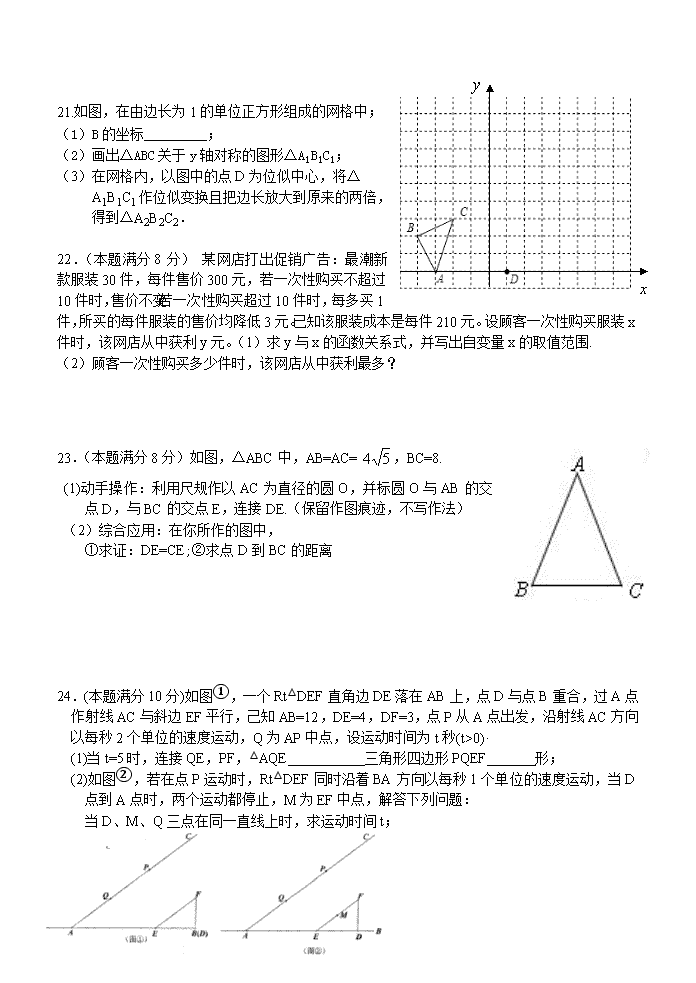
初三上学期期中复习二( 2020.11) 姓名 ‎ 一、精心选一选 ‎1．下列关于x的方程中，一定是一元二次方程的为（　）‎ ‎ A．x2﹣1=0 B．x2+2y +1=0 C．x2﹣2=（x+3）2 D．‎ ‎2．关于x的一元二次方程x2+kx﹣1=0的根的情况（　　）‎ ‎ A．有两个相等的实数根 B．有两个不相等的实数根 ‎ ‎ C．没有实数根 D．无法确定 ‎3．⊙O的半径为4，线段OP=4，则点P与⊙O的位置关系是（ ）．‎ ‎ A．点P在⊙O外 B．点P在⊙O内 C．点P在⊙O上 D．不能确定 ‎4．如图，AB是⊙O的直径，弦CD⊥AB，垂足为M，下列结论不一定成立的是( )‎ ‎ A．CM=DM　 　B．=　 C．∠ACD=∠ADC　 　D．OM=BM ‎（第9题）‎ ‎（第7题） ‎ ‎（第4题）‎ ‎ （第8题）‎ ‎7．如图，在△ABC中，点O为重心，则S△DOE：S△BOC=（　　）‎ ‎ A．1：4 B． 1：3 C． 1：2 D． 2：3‎ ‎8．如图所示，将△ABC的三边分别扩大一倍得到△A1B1C1，（顶点均在格点上），它们是以P点为位似中心的位似图形，则P点的坐标是（　） A．（-3，-3） B．（-4，-3） C．（-4，-4） D．（-3，-4）‎ ‎9．如图，以半圆的一条弦BC（非直径）为对称轴将弧BC折叠后与直径AB交 于点D，若，且AB＝10，则CB的长为（ ）‎ A． B． C． D．4‎ ‎10．如图，在平面直角坐标系xOy中，以原点O为圆心的圆过点A（13，0），直线y=与⊙O交于B、C两点，则弦BC长的最小值为（ ）‎ ‎ A． 22 B． 24 C． 10 D. 12‎ 二、仔细填一填 ‎ ‎11．已知m、n是一元二次方程x2+x﹣1=0的两个根，那么m+n=　　． （第10题图）‎ ‎12．在同一时刻物体的高度与它的影长成比例，在某一时刻，有人测得一高为1.8米的竹竿的影长为3米，某一高楼的影长为60米，那么高楼的实际高度是 米．‎ ‎13.如图，⊙O的内接四边形ABCD中，∠A=115°，则∠BOD=_____.‎ ‎14.如图，练习本中的横格线都平行，且相邻两条横格线间的距离都相等，同一条直线上的三个点A、B、C都在横格线上，若线段AB=2cm，则线段BC= cm.‎ ‎15．如图，一块直角三角板ABC的斜边AB与量角器的直径恰好重合，点D对应的刻度是58°，则∠ACD的度数为　　　　．‎ ‎(第16题图)‎ ‎（第13题） （第14题） （第15题）‎ ‎16．如图，AB 为⊙O 的直径，弦CD⊥AB 于E，已知CD=12，BE=3，则⊙O 的直径为_______‎ ‎17.⊙O中，弦AB的长恰等于半径，则弦AB所对圆周角是___ _____度．‎ ‎18．第15题图 如图，AB为⊙O的直径，C为⊙O上一点，弦AD平分∠BAC，交BC于点E，AB＝10，AD＝8，则DE的长为 .‎ ‎（第16题）‎ 三、解答题 ‎（第18题图）‎ ‎19.解一元二次方程：‎ ‎① ②‎ ‎ ③ ④ ‎ ‎20．如图，在△ABC中，点D，E，F分别在AB，BC，AC边上，DE∥AC，EF∥AB．‎ ‎（1）求证：△BDE∽△EFC．‎ ‎（2）设，①若BC＝12，求线段BE的长；‎ ‎②若△EFC的面积是20，求△ABC的面积．‎ ‎21.如图，在由边长为1的单位正方形组成的网格中；‎ ‎（1）B的坐标_________；‎ ‎（2）画出△ABC关于y轴对称的图形△A1B1C1；‎ ‎（3）在网格内，以图中的点D为位似中心，将△A1B1C1作位似变换且把边长放大到原来的两倍，得到△A2B2C2．‎ ‎22．（本题满分8分） 某网店打出促销广告：最潮新款服装30件，每件售价300元，若一次性购买不超过10件时，售价不变；若一次性购买超过10件时，每多买1件，所买的每件服装的售价均降低3元。已知该服装成本是每件210元。设顾客一次性购买服装x件时，该网店从中获利y元。（1）求y与x的函数关系式，并写出自变量x的取值范围.‎ ‎（2）顾客一次性购买多少件时，该网店从中获利最多？‎ ‎23．（本题满分8分）如图，△ABC中，AB=AC=，BC=8.‎ ‎(1)动手操作：利用尺规作以AC为直径的圆O，并标圆O与AB的交点D，与BC的交点E，连接DE.（保留作图痕迹，不写作法）‎ ‎（2）综合应用：在你所作的图中，‎ ‎①求证：DE=CE;②求点D到BC的距离 ‎24．(本题满分10分)如图①，一个Rt△DEF直角边DE落在AB上，点D与点B重合，过A点作射线AC与斜边EF平行，己知AB=12，DE=4，DF=3，点P从A点出发，沿射线AC方向以每秒2个单位的速度运动，Q为AP中点，设运动时间为t秒(t>0)·‎ ‎(1)当t=5时，连接QE，PF，△AQE 三角形四边形PQEF 形； ‎ ‎(2)如图②，若在点P运动时，Rt△DEF同时沿着BA方向以每秒1个单位的速度运动，当D点到A点时，两个运动都停止，M为EF中点，解答下列问题：‎ ‎ 当D、M、Q三点在同一直线上时，求运动时间t；‎ ‎ ‎ ‎25． 如图，在△ABC中，∠BAC=90°，点E在BC边上，且CA=CE，过A，C，E三点的⊙O交AB于另一点F，作直径AD，连结DE并延长交AB于点G，连结CD，CF．‎ ‎（1）求证：四边形DCFG是平行四边形；‎ ‎（2）当BE=4，CD=AB时，求⊙O的直径长．‎ O G F E D C B A O G F E D C B A ‎ ‎ ‎26. 如图，△ABC和△CDE都是等边三角形，点B、C、E三点在同一直线上，连接BD，AD，BD交AC于点F．（1）若AD2＝DF•DB，求证：AD＝BF；‎ ‎（2）若∠BAD＝90°，BE＝6．求DF的长．‎