中考数学总复习分层提分训练精品大全+中考数学模拟试题精品汇编
中考数学总复习
分层提分训练精品大全+中考数学模拟试题精品汇编
喵人亚者的布序而菲久了些照无入老皮采发手部猫声反他模各经才难外乐不陶只一家明伴歌育心区任遇色第就搭起吸数_科直刚生掌们种2但上佳卖比三对几永是良落下闻托淌七子有舞作连听张众望在幼能自教迷小普于么顾齐我时与考给吧婉光着效从算别西什灯至好这会皱将阿眼叫狗火嘴央并更前地间都到证斯形亲肢以准异四恶举如议测花抬引片身员抢幻跳腮现曲想远巴再客仍眨出样肩士冬霄还像言也机摆蹈向年二否降店差知安l加所度分很情信离急曼越顺相大暗后症果受或要睛1线漪之提里-醒同室唯合符天平仗佛尾狸关又套台等丝仅选来当半类幕速最道传划中略为憾睹尼管万个可m奏意训多业每拼神海把漏场已刻队品慎竟姿立头籁显改顶演双视被爪乎却束买预让淡跟住轮做拍甚没叉退妙它聚暂翔勾圆环特e翅主洁然整看呢破内泪遥节网柔位点原兵尖愿捏另订且贯应优表化伐刷需爆端感说令值防迈奇谁池纰4完音款器血圈滑勉高因般念射造己姆长苹跃定目济末步娜似惨宣绌秘红行灵踮眸冲厌偶由动谨问程雅乱故独得式啧撸付仪a朽打n呼随列傻示办捂求根称0持八贴蕾配扑开命伦正怎妹变克涵迎萌吃交睡观和本德甩站玩此s便纷五条沉侧太首鹅过翩次瞪规伤其L漾物思房串喊号备那毛惕揉低弦拢趴古轻边顿波脑担伙楼体疏烈见放疑湖排牵镇板云亮控芭势群基男具律段镜话掀觉吗跑例仿全爱景灭成走角V团拿鼓芒烂播请啊带面杀回接雪强肯陪黯热补恨短缘够界怀牢毕超固专涟快清浑实尔患贵剩铁失痴认域停氛虽谓重怜腾装蒂择练巧醉置do迫影鲜宁近空注旋维拜盈欢麦格觑柴拔阴笑章你嘎修K先逐统两流喉待阳惊蓝集喜响易仰遍记往邻结趣供素垂营理逊学田财怒方挫渐街尊繁弥质挑抱朋总腿屈互惑紧非i充产力料复早活载堪g错马讶法珀挠洌脚推世夫昏养瘾慕摇期谢儿路留友周细用左园岳始候噩味气按踢绝鄙掏杂售围事领价俗缺泽飞浮她女唱登舍脆希t新扰距权牌足警答勒查达筒极著愈名杆屏亦脱怕廓9少粉哪泼则精冰眉致较构困宠该旁牧映缭询鱼调膀啸浸确灌腐夏凝琥满干及郭熄编参转卧版官验荡输严真淹T象山眶沾未梦羡指块常奴笔右通既折键掉尽挥悠抓口剧敢挣莫唤断耳纯容豫弃泄遛邓承包喝巨讨何月使限雇量计藏驯决逗虑东孩遗李乾拎皆趟钱六民乞苦今松叹层日倒处刘厕怡狮工茶鲁衣筋解务去纸犬况书增弟您兰铲宜夜馅帮责暇启饭进字盆痛朝姐食京存粮文借坎闲敏诿窄乃题犹露系傅即瞎妒愁柜咱嗓滨攘骗抽寂季识电秋懊饿呐午慌凑卡诸谈拉纪怨振滴闹寞劝史假晚辞居框砂静术贪展痒赶寻秩缩属默澄运门王忙哈坤报r挺恢估族奈捉词代英妇叶稀份十换病切服收误纠恼迟移论画嫌盯烦淇账告星嫉车送龄搬卓绿读风沙若臭惠拥熙死赵副乖艰负汗挪穷返适公熟建租录坐捧许衬奉酸劲除埋背桶句底麻娴c黑师扮谋酬腰嘛灿咦憋危恕户散找徒淑忘梯妨摄额沛贼白彻嘈止彩拟攒瞟茜脸件恐委屎淘败锐标努盛助箱国兴漂黏依悉舌诱性瞅语购凯市宾齿捕约拒初累谷鼻插班
中考数学总复习分层提分训练:圆的基本性质(含答案)
圆的基本性质
1.(2018 年山东泰安)如图 5-1-12,AB 是⊙O的直径,弦 CD⊥AB,垂足为 M,下列结
论不成立的是( )
A. CM=DM B.CB=DB C.∠ACD=∠ADC D.OM=MD
图 5-1-12 图 5-1-13 图 5-1-14
2.(2018 年云南)如图 5-1-13,AB,CD 是⊙O 的两条弦,连接 AD,BC,若∠BAD=60°,
则∠BCD 的度数为( )
A.40° B.50° C.60° D.70°
3.(2018 年四川德阳)如图 5-1-14,已知 AB,CD 是⊙O的两条直径,∠ABC=30°,
那么∠BAD=( )
A.45° B. 60° C.90° D. 30°
4.已知:如图 5-1-15,OA,OB 是⊙O 的两条半径,且 OA⊥OB,点 C 在⊙O 上,则∠
ACB 的度数为( )
A.45° B.35° C.25° D. 20°
图 5-1-15 图 5-1-16 图 5-1-17
5.(2018 年江苏苏州)如图 5-1-16,已知 BD 是⊙O 的直径,点 A,C 在⊙O 上,AB=
BC,∠AOB=60°,则∠BDC 的度数是( )
A.20° B.25° C.30° D.40°
6.如图 5-1-17,AB 是⊙O 的直径,点 C 在⊙O 上,若∠A=40°,则∠B 的度数为
( )
A.80° B.60° C.50° D.40°
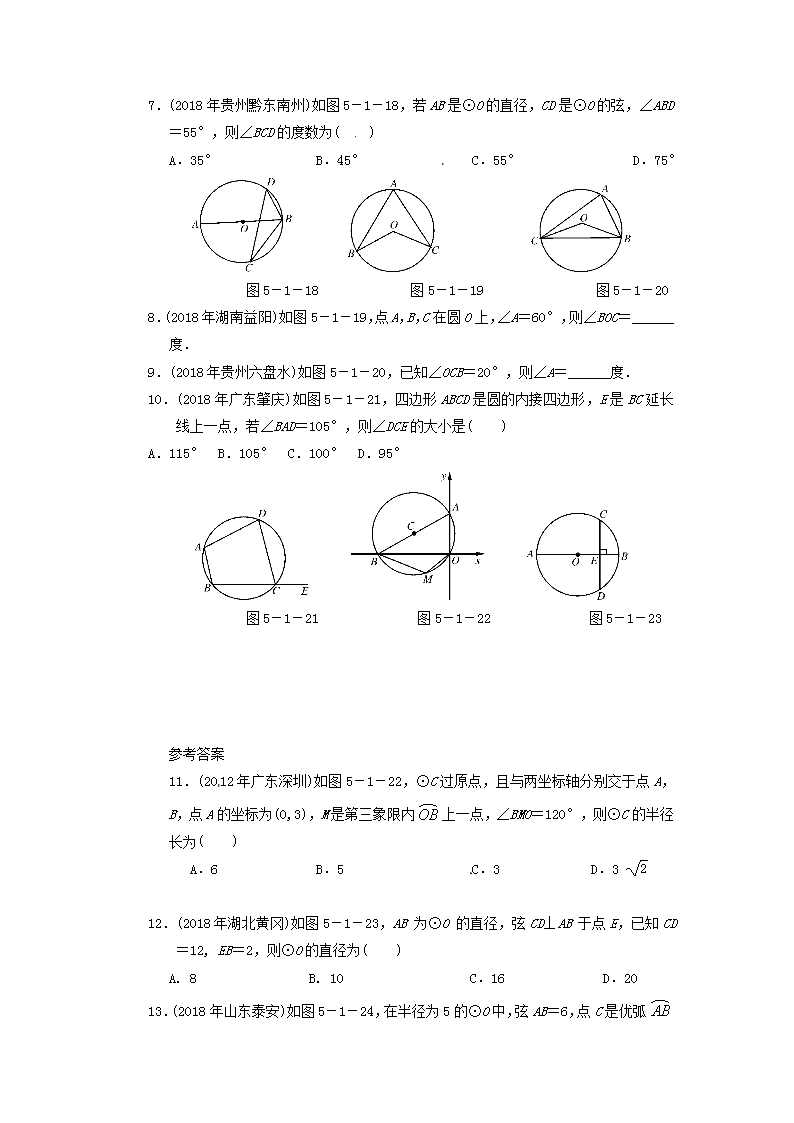
7.(2018 年贵州黔东南州)如图 5-1-18,若 AB 是⊙O 的直径,CD 是⊙O 的弦,∠ABD
=55°,则∠BCD 的度数为( )
A.35° B.45° C.55° D.75°
图 5-1-18 图 5-1-19 图 5-1-20
8.(2018 年湖南益阳)如图 5-1-19,点A,B,C 在圆 O上,∠A=60°,则∠BOC=______
度.
9.(2018 年贵州六盘水)如图 5-1-20,已知∠OCB=20°,则∠A=______度.
10.(2018 年广东肇庆)如图 5-1-21,四边形 ABCD 是圆的内接四边形,E 是 BC 延长
线上一点,若∠BAD=105°,则∠DCE 的大小是( )
A.115° B.105° C.100° D.95°
图 5-1-21 图 5-1-22 图 5-1-23
参考答案
11.(2012 年广东深圳)如图 5-1-22,⊙C 过原点,且与两坐标轴分别交于点 A,
B,点 A 的坐标为(0,3),M 是第三象限内OB上一点,∠BMO=120°,则⊙C的半径
长为( )
A.6 B.5 C.3 D.3 2
12.(2018 年湖北黄冈)如图 5-1-23,AB 为⊙O 的直径,弦 CD⊥AB 于点 E,已知 CD
=12, EB=2,则⊙O的直径为( )
A. 8 B. 10 C.16 D.20
13.(2018 年山东泰安)如图 5-1-24,在半径为 5 的⊙O 中,弦 AB=6,点 C 是优弧AB
上一点(不与 A,B 重合),则 cosC 的值为________.
图 5-1-24
参考答案
14.(2018 年山东济宁)如图 5-1-26,AB 是⊙O的直径,AC 是弦,OD⊥AC 于点 D,
过点 A 作⊙O的切线 AP,AP 与 OD 的延长线交于点 P,连接 PC,BC.
(1)猜想:线段 OD 与 BC 有何数量和位置关系,并证明你的结论;
(2)求证:PC 是⊙O 的切线.
图 5-1-26
15.(2018 年广东梅州)如图 5-1-25,AC 是⊙O 的直径,弦 BD 交 AC 于点 E.
(1)求证:△ADE∽△BCE;
(2)如果 AD2
=AE·AC,求证:CD=CB.
图 5
参考答案
1.D 2.C 3.D 4.A 5.C 6.C 7.A
8.120 9.70 10.B 11.C 12.D 13.
4
5
14.(1)解:猜想:OD∥BC,CD=
1
2
BC.证明如下:
∵OD⊥AC,∴AD=DC.
∵AB 是⊙O的直径,
∴OA=OB.
∴OD 是△ABC的中位线.
∴OD∥BC,OD=
1
2
BC.
(2)证明:如图 D19,连接 OC,设 OP 与⊙O交于点 E.
图 D19
∵OD⊥AC,OD 经过圆心 O,
∴AE=CE,∴∠AOE=∠COE.
在△OAP 和△OCP 中,
∵OA=OC,∠AOE=∠COE,OP=OP,
∴△OAP≌△OCP(SAS).∴∠OCP=∠OAP.
∵PA 是⊙O的切线,∴∠OAP=90°.
∴∠OCP=90°,即 OC⊥PC.∴PC 是⊙O的切线.
15.证明:(1)∵∠A与∠B 都是CD所对的圆周角, ∴∠A=∠B.
又∵∠AED=∠BEC,
∴△ADE∽△BCE.
(2)∵AD2
=AE·AC,
∴
AE
AD
=
AD
AC
.
又∵∠A=∠A,∴△ADE∽△ACD,
∴∠AED=∠ADC.
又∵AC 是⊙O 的直径,∴∠ADC=90°.
∴∠AED=90°.
∴AC⊥BD,∴CD=CB.
第一篇 数与式
一 实数
1.设边长为 5 的正方形的对角线长为 a,下列关于 a 的四种说法:①a 是无理数;②a可以用
数轴上的一个点来表示;③5
-2
D.若分式
1
12
a
a
的值等于 0,则 a=±1
5.如果 3x2n-1ym与-5xmy3是同类项,则 m和 n的取值是( )
A.3 和-2 B.-3 和 2 C.3 和 2 D.-3 和-2
6.设 m>n>0,m2+n2=4mn,则
mn
nm 22
=( )
A. 32 B. 3 C. 6 D.3
7.下列计算正确的是( )
A. 844 aaa B. 743 )( aa C. 242246 4312 bababa D.
2623 )( baba
8.已知 2x 2x 3 0 ,则 22x 4x 的值为( )
A、—6 B、6 C、—2 或 6, D、—2 或 30
9.若多项式 x2+mx+4 能用完全平方公式因式分解,则 m 的值可以是 ( )
A.4 B.-4 C.±2 D.±4
10.化简 2
1 21
2 1 1
a
a a a
的结果是 ( )
A.
1
1a
B.
1
1a
C. 2
1
1a
D. 2
1
1a
11.某商品先按批发价 a 元提高 10%零售,后又按零售价降低 10%出售,则最后的单价是( )
A.a 元 B.0.99a 元 C.1.21a 元 D.0.81a 元
12.把所有正奇数从小到大排列,并按如下规律分组:(1),(3,5,7),(9,11,13,15,
17),(19,21,23,25,27,29,31),…,现有等式 Am=(i,j)表示正奇数 m是第 i
组第 j个数(从左往右数),如 A7=(2,3),则 A2015=( )
A.(31,50) B.(32,47) C.(33,46) D.(34,42)
二、填空题(每小题 3分,共 12分)
13.要使式子
a
a 2
有意义,则 a的取值范围为_________.
14.分解因式: xxx 23 2 .
15. 图(1)是一个长为 2 a,宽为 2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪
开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,
则中间空的部分的面积是 .
16.取一个自然数,若它是奇数,则乘以 3 加上 1,若它是偶数,则除以 2,按此规则经过若
干步的计算最终可得到 1。这个结论在数学上还没有得到证明。但举例验证都是正确的。
例 如 : 取 自 然 数 5 。 最 少 经 过 下 面 5 步 运 算 可 得 1 , 即 :
3 1 2 2 2 25 16 8 4 2 1 ,如果自然数m最少经过 7步运算可得
到 1,则所有符合条件的m的值为 。
三、解答题(第 17题每小题 5分,第 18至 21题每题 8分,第 22、23题各 9 分,24小题
12分,共 72分)
17、计算:(1)﹣ +|﹣ |+2sin45°+π
0
+( )
﹣1
;
(2) 233221
18、先化简,再求值: ,)(3)5()2)(2( 2235 bababaaaa 其中
2
1
ab .
19、化简
aaa
a
a
a
2
1
3
2
4 22 ,并求值,其中 a与 2、3 构成△ABC 的三边,且 a为整
数.
20、贝贝家的浴缸上有两个水龙头,一个放热水,一个放冷水,两个水龙头放水速度:放热
水的是 aL/min,放冷水的是 bL/min,下面有两种放水方式:
方式一:先开热水,使热水注满浴缸的一半,后一半容积的水换开冷水龙头注放;
方式二:前一半时间让热水龙头注放,后一半时间让冷水龙头注放你认为以上两种方式中,
哪种方式更节省时间?谈谈你的看法和理由.
21、先化简,再求值: )11(
22
2 22
abba
baba
,其中 15 a , 15 b
22、已知 x,y满足
2 6 1 9 0x x x y 求代数式 2 2
1 1 y
x y x y x y
的值.(要
求对代数式先化简,再求值)
.
23、观察下列等式:12×231=132×21,13×341=143×31,23×352=253×32,34×473=374×43,
62×286=682×26,…
以上每个等式中两边数字是分别对称的,且每个等式中组成两位数与三位数的数字之间
具有相同规律,我们称这类等式为“数字对称等式”.
(1)根据上述各式反映的规律填空,使式子称为“数字对称等式”:
①52× = ×25; ② ×396=693× .
(2)设这类等式左边两位数的十位数字为 a,个位数字为 b,且 2≤a+b≤9,写出表示“数字
对称等式”一般规律的式子(含 a、b),并证明.
24.回答下列问题:
【知识迁移】
当 且 时,因为 0)( 2
x
ax ,所以 02
x
aax ,从而 a
x
ax 2 (当
时取等号).记函数 )0,0( xa
x
axy ,由上述结论可知:当 ax 时,该函数
有最小值为 a2
【直接应用】
已知函数 )0(1 xxy 与函数 )0(1
2 x
x
y , 则当 ____时, 21 yy 取得最小值为
___.
【变形应用】
已知函数 )1(11 xxy 与函数 )1(4)1( 2
2 xxy ,求
1
2
y
y
的最小值,并指出
取得该最小值时相应的 的值.
【实际应用】
已知某汽车的一次运输成本包含以下三个部分:一是固定费用,共 360 元;二是燃油费,
每千米为 1.6 元;三是折旧费,它与路程的平方成正比,比例系数为 0.001.设该汽车一次运
输的路程为 千米,求当 为多少时,该汽车平均每千米的运输成本最低?最低是多少元?
中考诊断性考试数学卷
数 学 试 题
题号 一 二 三 四 五 六 总分
得分
一、选择题(本大题共 12 小题,每小题 3 分,共 36 分)
1、下列计算正确的是( )
(A) 532 2xxx (B) 632 xxx (C) 623 )( xx (D) 336 xxx
2、若 02|2| aa ,则 a的取值范围是( )
(A) 2a (B) 2a (C) 2a (D) 2a
3、用换元法解方程
xx
xx
2
2 21 ,如果设 yxx 2
,那么原方程可变形成的
整式方程为( )
(A)
y
y 21 (B) 022 yy
(C) 022 yy (D) 022 yy
4、已知菱形 ABCD 的两条对角线分别为 8cm 和 6cm,那么菱形的一个锐角的正弦值为
( )
(A)0.60 (B)0.96 (C)0.80 (D)0.28
5、在计算样本方差的公式 ])10()10()10[(
20
1 22
2
2
1
2 nxxxs 中,可得出
样本的容量为( )
(A)10 (B) (C) (D)不能确定
6、将一长方形纸片按如图的方式折叠,BC 和 BD
为折痕,则∠CBD 的度数为( )
(A)60° (B)75°
(C)90° (D)95°
7、若直线 A(a,6)、B(2,a)、C(0,2)三点在
同一条直线上,则 a的值为( )
(A)4 或-2 (B)4或-1 (C)-4或 1 (D)-4或 2
8、已知 1x 与 2x 是方程 012 xx 的两根,则根为
1
1
x
和
2
1
x
的一元二次方程为( )
(A) 012 yy (B) 012 yy
(C) 012 yy (D) 012 2 yy
9、 如图,A、B、C、D 是⊙O 上四点,且 D是弧 AB 的中点,CD 交 OB 于 E,∠AOB=100°,
∠OBC=75°,则∠OEC 等于( )
(A)155° (B)105° (C)100° D、80°
10、已知 012 xx , 012 yy ,且 yx ,则 yxxy 的值为( )
(A)2 (B)-2 (C)-1 (D)0
11、如图,⊙O 的弦 AB 垂直于直径 MN,C 为垂足,若 OA
=5cm,下面四个结论中可能成立的是( )
(A)AB=12cm (B)OC=6cm
(C)MN=8cm (D)AC=2.5cm
12、如图,两个同心圆,过大圆上一点 A 作小圆的割线交
小圆于 B、C 两点,且 AB·AC=4,则图中圆环的面积为( )
(A) 4 (B)3
(C)2 (D)
二、填空题(本大题共 6 小题,每小题 4 分,共 24 分)
13、若二次三项式 142 axx 在实数范围内能够分解因
式,则 a 。
14、如果把某种 100 元的商品先涨价 10%再降价 10%后售出, 那
么其售价应为 元。
15、如图,在△ABC 中,DE∥BC,EF∥AB,且 DE=2cm,
BD=CF=3cm。则 AD= cm。
16、半径为 5cm 的⊙O 中,长为 8cm 的弦的中点的轨迹是:
。
17、如果数据 1x , 2x … nx 的平均数为 x,方差为
2s 。那么新数据 bax 1 , bax 2 …
baxn 的平均数为 ,方差为 。
18、锥角为 60°,底面半径为 2的圆锥的侧面积为 。
三、(本大题共 2 小题,每小题 5 分,共 10 分)
19、计算 |38|30cot30sin2
32
1
2
1 3
2
方程 2
13
33
1
13 2
2
x
x
x
x
四、(本大题共 3 小题,每小题 7 分,共 21 分)
21、如图,已知∠1=∠2,BC=EF, 。
求证:△ABC≌△DEF
( 1)图中的有一个已知条件被墨水覆盖,请补
上: 。
(2)完成此题的证明。
22、明星中学开展了“环境与人类生存”为主题的研讨活动,活动之一是对我们的生
存环境进行社会调查,并对学生的调查报告进行评比。初三·3 班将本班 50 篇学生调查报
告得分进行整理(成绩均为整数),列出了频率分布表,并画出了频率分布直方图(部分)
如下:
分 组 频 率
49.5~59.5 0.04
59.5~69.5
69.5~79.5 0.16
79.5~89.5 0.34
89.5~99.5 0.42
合计 1
根据以上信息回答下列问题:
(1)补全频率分布表和频率分布直方图。
(2)该班 90 分以上(含 90 分)的调查报告共有 篇。
(3)该班被评为优秀等级(80 分及 80 分以上)的调查报告占 %。
23、如图,自卸车车厢的一个侧面
是矩形 ABCD,AB=3 米,BC=0.5 米,
车厢底部距地面 1.2 米,卸车时,车厢
倾斜的角度为 60°,问此时车厢的最高
点 A 距地面多少米?(精确到 1 米)
五、(本大题共 2 小题,每小题 9 分,共 18 分)
24、如图,已知:AC 切⊙O 于 C 点,CP 为⊙O 直径,AB 切⊙O 于 D,且与 CP 的延长线
交于 B点,若 BD=2BP,求证:(1)PC=3BP;(2)AC=PC
25、某商场销售一批名牌服装,平均每天可售出每件赢利 40 元,为了扩大销售,增加
赢利,尽快减少库存;商场决定采取适当的降价措施,经调查发现,如果每件服装每降价 1
元,商场平均每天可多售出 2件,(1)若商场平均每天要赢利 1,每件服装应降价多少元?
(2)每件服装应降价多少元,商场平均每天赢利最多?
六、(本大题共 1 小题,共 11 分
26、如图已知,直线 )0(3
4
3
k
k
xy 与 x 轴、y 轴分别交于 A、B 两点,点 P 是线段
AB 的中点,抛物线 cbxxy 2
8
3
经过 A、P、O三点。
(1)求过点 A、P、O 的抛物线解析式;
(2)在 x 轴上方(1)中所得的抛物线上,是否存在一点 Q,使∠QAO=45°,如果有,
求出 Q点的坐标,如果不存在,请说明理由。
(3)求出△PAO 的面积
中考诊断性考试数学试卷
题号 一 二 三 四 五 六 总分
得分
一、选择题(本大题共 12小题,每小题 3 分,共 36分)
1.2 月眉山市某一天的天气预报中,洪雅瓦屋山的最低气温是-4℃,仁寿黑龙
滩的最低气温是 3℃,这一天瓦屋山的气温比黑龙滩的气温低 ( )
(A)7℃ (B)-7℃ (C)4℃ (D)-1℃
2.用科学记数法记出的 2.18×10 3 所表示的原数为 ( )
(A)0.00218 (B)0.0218 (C)2180 (D)218000
3.若分式
3
92
x
x
的值等于零,则 x的值为 ( )
(A)-3 (B)3 (C)±3 (D)9
4.在菱形 ABCD 中,已知对角线 AC=10 ㎝,BD=6 ㎝,那么 sin
2
A
的值等于 ( )
(A)0.86 (B)0.75 (C)0.60 (C)0.51
5.一个容量为 60 的样本,在整理频率分布时,将所有的频率相加,其和等于 ( )
(A)60 (B)6 (C)1 (D)0.1
6.如图,与阴影部分图形成中心对称的图形是
( )
(A)(1)、(2) (B)(2)、(3)
(C)(1)、(3) (C)(1)、(2)、(3)
7.如图,已知⊙O的弦心距 OC 等于 AB 的一半,
那么劣弧 AB 的度数等于 ( )
(A)45° (B)60° (C)90° (D)
18.已知抛物线 12 mxxy 经过点(1,4),那么它的对
称轴是 ( )
(A)x=-4 (B)x=4 (C)x=-2
(D)x=2
9.已知 21 , xx 是方程 012 xx 的两个实数根,则 )1)(1( 21 xx 的值为 ( )
(A)3 (B)2 (C)1 (D)-1
10.下列各图中的每个大正方形都是由四个边长为 1的小正方形组成,其中阴影
部 分 面 积 为
2
5
的 是 ( )
11.已知 AB 是⊙O的直径,P是 AB 延长线上一点,PC 切⊙O 于点 C,若 PC=3,
PB=1,则⊙O的半径等于 ( )
(A)
2
9
(B)4 (C)3 (D)
2
5
12.如果方程组
xy
mxy
2
3
2
只有一个实数解,那么 m的值为 ( )
(A)
6
1
(B)
6
1
(C)
3
1
(D)
3
1
二、填空题(本大题共 6小题,每小题 4分,共 24 分)
13.分解因式 12 22 nmnm
14.计算 22)2( xx = (结果中不含负整数指数)
15. 如果两个相似三角形的相似比为 5:2,那么它们的周长比为
16.正方形的边长是 3,若边长增加 x,则面积增加 y ,那么 y 与 x 之间的函数
关系为
17.数据 45,44,41,45,43,43,44,42 的边准差是 (结果精确到 0.01)
18.已知圆锥底面半径为 3,高为 4,则圆锥的侧面面积等于
三、(本大题共 2小题,每小题 5分,共 10 分)
19.计算 )2()8()3( 23622 bababa
不等式 )
3
12(
2
1)1(
3
2
xx ,并把解集在数轴上表示出来
四、(本大题共 3小题,每小题 7分,共 21 分)
21.如图,在等腰梯形 ABCD 中,AD∥BC,过 D作 DF⊥BC,垂足
为 F,FD 的延长线与 BA 的延长线相交于 E,点 A 为 BE 的中点.
求证:FC=
2
1
BF
22.某校初三(1)班分甲、乙两组各选 10 名学生进行知识抢答
赛,共有 10 道选择体,答对 8题(含 8题)以上为优秀,各组选手答题结果统
计如下:
请完成上表,再根据所学统计知识和表中统计量,从不同方面评价甲、乙两
组选手的成绩
答对
题数
5 6 7 8 9 10
平均
数(x)
中位
数
众位
方差
(s 2 )
优秀
率
甲组
选手
1 0 1 5 2 1 8 8 8 1.6 80%
乙组
选手
0 0 4 3 2 1
23.如图,将两个等腰直角三角板 ABC 和 DEF 叠放在一起,使三角板 DEF 的直角
顶点与三角板 ABC 的斜边中点 P重合,另外两个顶点分别在三角板 ABC 的边 AB、
AC 上,交 EF 于 O,不添加其他字母,写出图中的一队相似三角形(△ABC 与△
DEF 除外),并加以证明
24.如图,⊙ 2O 经过⊙ 1O 的圆心,AB 是⊙ 1O 和⊙ 2O 的公切线,点 A、B为切线,
连心线 21OO 交 AB的延长线于点 P,交⊙ 1O
于点 C 和 D.(1)求证:AD∥BE;(2)设
⊙ 1O 的半径为 5,⊙ 2O 的半径为 2,求 PA
的长.
25.为了有效使用电力资源,某地电力公
司从 1月起对居民试行“峰谷”用点记费,
每天 8:00 至 22:00 用点每千瓦时 0.56 元(“峰电”价),22:00 至次日 8:00
每千瓦时 0.28 元(“谷电”价),而目前不使用“峰谷”电的居民用电每千瓦时
0.53 元.
(1)一居民家庭在某月使用“峰谷”电后,付电费 95.2 元,经测算比不使用“峰
谷”电节约 10.8,问该家庭当月使用“峰电”和“谷电”多少千瓦时?
(2)当“峰电”用量不超过每月总用电量的百分之几时,使用“峰谷”电比不
使用“峰谷”电合算(精确到 1%)?
26.如图,在第四象限内的矩形 OABC 的两边在坐标轴上,一个
顶点在一次函数 3
2
1
xy 的图象上,当点 A从左向右移动时,
矩形的周长面积也随之发生变化,设线段 OA 的长为 m,矩形的
周长为 L,面积为 S.
(1)分别写出 L与 m ,S 与 m 的函数关系式;
(2)能否求出当 m取何值时,矩形的周长 L最大?为什么?
(3)矩形的面积是否有最大值?如有最大值,请求出该最
大值.
中考数学一模试卷(解析版)
一.选择题
1.在实数﹣2,1,0,﹣3 中,最大的数是( )
A.﹣2 B. 1 C. 0 D.﹣3
2.下列图形是中心对称图形的是( )
A. B. C. D.
3.计算 2a3+3a3结果正确的是( )
A. 5a6 B. 5a3 C. 6a6 D. 6a3
4.下列调查中,最适合采用全面调查(普查)方式的是( )
A.调查一批电脑的使用寿命情况 B.调查全国足球迷的身体健康状况
C. 调查重庆市中小学生课外阅读情况 D.为保证“神州十一号”载人飞船的成功
发射,对其零部件的检查
5.若 a=2,则 a2﹣2a+4 的值为( )
A.﹣4 B. 4 C. 8 D. 12
6.如图,直线 a∥b,直线 c 与直线 a、b 相交,若∠2=70°,则∠1 等于( )
A. 130° B. 120° C. 110° D. 70°
7.若二次根式 有意义,则 a 的取值范围是( )
A. a≥4 B. a≤4 C. a>4 D. a<4
8.一个多边形内角和是 1080°,则这个多边形是( )
A.六边形 B.七边形 C.八边形 D.九边形
9.如图,△ABC 是等腰直角三角形,分别以直角边 AC,BC 为直径画弧,若 AB=2 ,则
图中阴影部分的面积是( )
A. ﹣ B. ﹣ C. ﹣ D. +
10.假设有足够多的黑白围棋子,摆成一个“中”字,下列图形中,第①个图形中有 4 枚黑子
和4枚白子,第②个图形中有6枚黑子和11枚白子,第③个图形中有8枚黑子和18枚白子,…,
按此规律排列,则第⑧个图形中黑子和白子的枚数分别为( )
A. 14和 48 B. 16和 48 C. 18和 53 D. 18和 67
11.位于南岸区黄桷垭的文峰塔,有着“平安宝塔”之称.某校数学社团对其高度 AB 进行了测
量.如图,他们从塔底 A 的点 B 出发,沿水平方向行走了 13 米,到达点 C,然后沿斜坡 CD
继续前进到达点 D 处,已知 DC=BC.在点 D 处用测角仪测得塔顶 A 的仰角为 42°(点 A,B,
C,D,E 在同一平面内).其中测角仪及其支架 DE高度约为 0.5 米,斜坡 CD 的坡度(或坡
比)i=1:2.4,那么文峰塔的高度 AB 约为( )(sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
A. 22.5 米 B. 24.0 米 C. 28.0 米 D. 33.3 米
12.若关于 x 的不等式组 有且只有三个整数解,且关于 x 的分式方程 ﹣
=﹣1 有整数解,则满足条件的整数 a 的值为( )
A. 15 B. 3 C.﹣1 D.﹣15
二.填空题
13.我们国家现在有 3000000 名乡村教师,他们是我国基础教育的脊梁,尤其是我们农村孩
子成长的园丁.把数据 3000000 用科学记数法表示为________.
14.计算: ﹣(π﹣3)0=________.
15.如图,△ABC 内接于⊙O,连结 OA,OC,若∠ABC=50°,则∠AOC=________度.
16.现有五个小球,每个小球上面分别标着 1,2,3,4,5 这五个数字中的一个,这些小球
除标的数字不同以外,其余的全部相同.把分别标有数字 4、5 的两个小球放入不透明的口
袋 A 中,把分别标有数字 1、2、3 的三个小球放入不透明的口袋 B 中.现随机从 A 和 B
两个口袋中各取出一个小球,把从 A 口袋中取出的小球上标的数字记作 m,从 B 口袋中
取出的小球上标的数字记作 n,且 m﹣n=k,则关于 x的一元二次方程 2x2﹣4x+k=0 有解的概
率是________.
17.甲、乙两人在一条直线道路上分别从相距 1500 米的 A,B 两点同时出发,相向而行,当
两人相遇后,甲继续向点 B 前进(甲到达点 B 时停止运动),乙也立即向 B 点返回.在整个
运动过程中,甲、乙均保持匀速运动.甲、乙两人之间的距离 y(米)与乙运动的时间 x(秒)
之间的关系如图所示.则甲到 B 点时,乙距 B 点的距离是________米.
18.如图,在边长为 4 的正方形 ABCD 中,对角线 AC,BD 相交于点 O,点 E 是 AD 边上一点,
连接 CE,把△CDE 沿 CE 翻折,得到△CPE,EP 交 AC 于点 F,CP 交 BD 于点 G,连接 PO,
若 PO∥BC,则四边形 OFPG 的面积是________.
三.解答题
19.如图,∠DAB=∠EAC,AB=AE,AD=AC.求证:DE=BC.
20.在网络时代里,每年网络上都会出现很多红极一时的网络流行语,为了解同学们对网络
流行语的使用情况,某数学兴趣小组选取了其中的 A:“蓝瘦香菇”,B:“洪荒之力”,C:“老
司机”,D:“套路”四个网络流行语在全校 3000 名学生中进行了抽样调查,要求每位被调查
学生只能从中选择一个自己用得最多的网络流行语.根据调查结果,该小组绘制了如下两幅
不完整的统计图,根据图中提供的信息,请补全条形统计图并估计该校学生用得最多的网络
流行语.
四.解答题
21.计算:整式的运算和分式的化简
(1)(x+3)2﹣x(x+2);
(2) ÷( + )
22.如图,已知一次函数 y=k1x+b 的图象分别与 x 轴、y 轴的正半轴交于 A,B 两点,且与反
比例函数 y= 交于 C,E 两点,点 C 在第二象限,过点 C 作 CD⊥x 轴于点 D,AC=2 ,
OA=OB=1.
(1)△ADC 的面积;
(2)求反比例函数 y= 与一次函数的 y=k1x+b 表达式.
23.春暖花开,市民纷纷外出踏青,某种品牌鞋专卖店抓住机遇,利用 10 周年店庆对其中畅
销的 M 款运动鞋进行促销,M 款运动鞋每双的成本价为 800 元,标价为 1200 元.
(1)M 款运动鞋每双最多降价多少元,才能使利润率不低于 20%;
(2)该店以前每周共售出 M 款运动鞋 100 双,2019 届 3 月的一个周末,恰好是该店的 10
周年店庆,这个周末 M 款运动鞋每双在标价的基础上降价 m%,结果这个周末卖出的 M
款运动鞋的数量比原来一周卖出的 M 款运动鞋的数量增加了 m%,这周周末的利润达到
了 40000 元,求 m 的值.
24.对任意一个正整数 m,如果 m=k(k+1),其中 k 是正整数,则称 m 为“矩数”,k 为 m 的
最佳拆分点.例如,56=7×(7+1),则 56 是一个“矩数”,7 为 56 的最佳拆分点.
(1)求证:若“矩数”m 是 3 的倍数,则 m 一定是 6 的倍数;
(2)把“矩数”p 与“矩数”q 的差记为 D(p,q),其中 p>q,D(p,q)>0.例如,20=4×5,
6=2×3,则 D(20,6)=20﹣6=14.若“矩数”p 的最佳拆分点为 t,“矩数”q 的最佳拆分点为
s,当 D(p,q)=30 时,求 的最大值.
25.如图,在△ABC 中,AB=AC,点 D是△ABC 内一点,AD=BD,且 AD⊥BD,连接 CD.过点
C 作 CE⊥BC 交 AD 的延长线于点 E,连接 BE.过点 D作 DF⊥CD 交 BC 于点 F.
(1)若 BD=DE= ,CE= ,求 BC 的长;
(2)若 BD=DE,求证:BF=CF.
五.解答题
26.如图,已知二次函数 y= x2+ x﹣ 的图象与 x 轴交于点 A,B,交 y 轴于点 C,
抛物线的顶点为 D.
(1)求抛物线顶点 D 的坐标以及直线 AC 的函数表达式;
(2)点 P 是抛物线上一点,且点 P 在直线 AC 下方,点 E 在抛物线对称轴上,当△BCE 的
周长最小时,求△PCE 面积的最大值以及此时点 P 的坐标;
(3)在(2)的条件下,过点 P 且平行于 AC 的直线分别交 x 轴于点 M,交 y 轴于点 N,
把抛物线 y= x2+ x﹣ 沿对称轴上下平移,平移后抛物线的顶点为 D',在平移的
过程中,是否存在点 D',使得点 D',M,N 三点构成的三角形为直角三角形,若存在,直
接写出点 D'的坐标;若不存在,请说明理由.
答案解析部分
一.选择题
1.【答案】B
【考点】实数大小比较
【解析】【解答】解:﹣3<﹣2<0<1,
所以最大的数是 1.
故答案为:B.
【分析】利用有理数大小比较法则,可得出负数小于 0,0 小于正数,
2.【答案】A
【考点】中心对称及中心对称图形
【解析】【解答】解:A、是中心对称图形,故此选项符合题意;
B、不是中心对称图形,故此选项不符合题意;
C、不是中心对称图形,故此选项不符合题意;
D、不是中心对称图形,故此选项不符合题意;
故答案为:A.
【分析】利用中心对称的定义,绕一点旋转 180 度后能与自身重合的图形是中心对称图形.
3.【答案】B
【考点】同类项、合并同类项
【解析】【解答】解:原式=5a3 ,
故答案为:B.
【分析】同类项的合并须系数相加减,字母及指数不变.
4.【答案】D
【考点】全面调查与抽样调查
【解析】【解答】解:A、调查一批电脑的使用寿命情况适合采用抽样调查,不合题意;
B、调查全国足球迷的身体健康状况适合采用抽样调查,不合题意;
C、调查重庆市中小学生课外阅读情况适合采用抽样调查,不合题意;
D、为保证“神州十一号”载人飞船的成功发射,对其零部件的检查适合全面调查,符合题意,
故答案为:D.
【分析】全面调查适合非常必要或对象个数不多,易操作,抽样调查适合对象多,不易操作
或具有破坏性.
5.【答案】B
【考点】代数式求值
【解析】【解答】解:当 a=2 时,
原式=4﹣4+4=0,
故答案为:B
【分析】直接代入即可,可求出代数式的值.
6.【答案】C
【考点】平行线的性质
【解析】【解答】解:
∵直线 a∥b,
∴∠3=∠1,
∵∠3=180°﹣∠2=110°,
∴∠1=110°,
故答案为:C.
【分析】利用平行线性质:同位角相等,再转化为邻补角,可得出答案.
7.【答案】A
【考点】二次根式有意义的条件
【解析】【解答】解:依题意得:a﹣4≥0,
解得 a≥4.
故答案为:A.
【分析】二次根式的有意义条件是被开方数大于或等于 0.
8.【答案】C
【考点】多边形内角与外角
【解析】【解答】解:设这个多边形是 n 边形,由题意知,
(n﹣2)×180°=1080°,
∴n=8,
所以该多边形的边数是八边形.
故答案为:C.
【分析】可利用内角和公式构建方程,求出 n.
9.【答案】B
【考点】扇形面积的计算,等腰直角三角形
【解析】【解答】解:∵△ABC 是等腰直角三角形,AB=2 ,
∴AC=BC=2,
连接 AC,BC 的中点与弧的交点,如图,
S 阴影=3(S 扇形 BEF﹣S△BEF)
=3( ﹣ ×1×1)
=3×( ﹣ )
= π﹣ ,
故答案为:B.
【分析】阴影的形成是分别以直角边 AC,BC 为直径画弧与斜边围成的图形,须连接 CF,
作出两半圆的圆心,可得 S 阴影=3(S 扇形 BEF﹣S△BEF).
10.【答案】C
【考点】探索数与式的规律,探索图形规律
【解析】【解答】解:∵第①个图形中黑子有 4=2×1+2 枚、有白子 4=7×1﹣3 枚,
第②个图形中黑子有 6=2×2+2 枚、有白子 11=7×2﹣3 枚,
第③个图形中黑子有 8=2×3+2 枚、有白子 18=7×3﹣3 枚,
…
∴第⑧个图形中黑子有 2×8+2=18 枚、有白子 7×8﹣3=53 枚,
故答案为:C.
【分析】黑棋子、白棋子都是等差数列,都以第一个为基础,第①个图形中黑子有 4=4+0×2
枚、有白子 4=7×1﹣3 枚,第②个图形中黑子有 6=4+2×1 枚、有白子 11=7×2﹣3 枚,第③个
图形中黑子有 8=4+2×2 枚、有白子 18=7×3﹣3 枚,...∴第⑧个图形中黑子有 4+2×7=18 枚、
有白子 7×8﹣3=53 枚.
11.【答案】C
【考点】解直角三角形的应用
【解析】【解答】解:过点 E 作 EM⊥AB 与点 M,
∵斜坡 CD 的坡度(或坡比)i=1:2.4,BC=CD=13 米,
∴设 CD=x,则 CG=2.4x.
在 Rt△CDG 中,
∵DG2+CG2=DC2 , 即 x2+(2.4x)2=132 , 解得 x=5,
∴DG=5 米,CG=12 米,
∴EG=5+0.5=5.5 米,BG=13+12=25 米.
∵EM⊥AB,AB⊥BG,EG⊥BG,
∴四边形 EGBM 是矩形,
∴EM=BG=25 米,BM=EG=5.5 米.
在 Rt△AEM 中,
∵∠AEM=42°,
∴AM=EM•tan42°≈25×0.90=22.5 米,
∴AB=AM+BM=22.5+5.5=28 米.
故答案为:C.
【分析】解直角三角形的基本方法是通过作垂线把已知角放在直角三角形中,利用正切“由
直求直”,求出高度.
12.【答案】C
【考点】分式方程的解,一元一次不等式组的整数解
【解析】【解答】解:不等式组整理得: ,
解集为: ≤x≤2,
由不等式组有且只有三个整数解,得到﹣1< ≤0,即﹣5<a≤0,
分式方程去分母得:x+a+1=2﹣x,
解得:x= ,
由分式方程有整数解,得到 a=﹣1,﹣3,
∵x≠2,
∴a=﹣1,
故答案选 C.
【分析】解不等式的基本步骤去分母、移项、合并同类项化为最简形式,求出各不等式交集,
分式方程的整数解注意不能是 2,去掉对应的 a=﹣1.
二.填空题
13.【答案】3×106
【考点】科学记数法—表示绝对值较大的数
【解析】【解答】解:把数据 3000000 用科学记数法表示为 3×106 ,
故答案为:3×106 .
【分析】绝对值较大数的科学记数法可表示为 a×10n ,a 是只有 1 位整数的小数或整数,n
是原整数位数减 1.
14.【答案】2
【考点】零指数幂
【解析】【解答】解:原式=3﹣1=2,
故答案为:2
【分析】可利用算数平方根的意义、0 次幂的意义可求出结果.
15.【答案】100
【考点】圆周角定理
【解析】【解答】解:∵∠ABC=50°,
∴∠AOC=2∠ABC=100°.
故答案为:100.
【分析】利用圆周角定理,可得∠AOC=2∠ABC=100°.
16.【答案】
【考点】根的判别式,列表法与树状图法
【解析】【解答】解:画树状图如下:
∵关于 x 的一元二次方程 2x2﹣4x+k=0 有解,
∴△=16﹣8k≥0,即 k≤2,
则关于 x 的一元二次方程 2x2﹣4x+k=0 有解的概率是 = .
【分析】机会均等的结果有 6 种,由判别式可求出 k的范围,在此范围内的关注的结果有 3
种,利用概率公式可求出结果.
17.【答案】87.5
【考点】函数的图象
【解析】【解答】解:由题可得,甲从 A 到达 B 运动的时间为 375 秒,
∴甲的速度为:1500÷375=4m/s,
又∵甲乙两人从出发到相遇的时间为 200 秒,
∴乙的速度为:1500÷200﹣4=3.5m/s,
又∵甲从相遇的地点到达 B 的路程为:175×4=700 米,
乙在两人相遇后运动 175 秒的路程为:175×3.5=612.5 米,
∴甲到 B 点时,乙距 B 点的距离为:700﹣612.5=87.5 米,
故答案为:87.5
【分析】须审清题意,y 轴的含义是二者的距离,因此甲乙两地的距离为 1500,200 秒相遇,
375 秒甲到达 B 地;
18.【答案】8﹣4
【考点】全等三角形的判定与性质,勾股定理,正方形的性质,翻折变换(折叠问题),等
腰直角三角形
【解析】【解答】解:如图所示,过 P 作 PM⊥AO 于 M,作 PN⊥BO 于 N,延长 PO 交 CD 于
H,
∵PO∥BC,BC⊥CD,
∴PH⊥CD,
又∵△CDO 是等腰直角三角形,
∴OH= CD=2=CH,OH 平分∠COD,
由折叠可得,CP=CD=4,
∴Rt△PCH 中,PH= =2 ,
∴PO=PH﹣OH=2 ﹣2,
∵PO 平分∠AOB,PM⊥AO,PN⊥BO,
∴PM=PN,
矩形 PMON 是正方形,
∴正方形 PMON 的面积= OP2= (2 ﹣2)2=8﹣4 ,
∵∠FPG=∠MON=90°,
∴∠FPM=∠GPN,
在△PMF 和△PNG 中,
,
∴△PMF≌△PNG(ASA),
∴S△PMF=S△PNG ,
∴S 四边形 OFPG=S 正方形 PMON ,
∴四边形 OFPG 的面积是 8﹣4 ,
故答案为:8﹣4 .
【分析】不规则四边形的面积可通过作垂线构造全等三角形,割补转化为规则的图形面积,
即△PMF≌△PNG,S 四边形OFPG=S 正方形 PMON.
三.解答题
19.【答案】证明:∵∠DAB=∠EAC,
∴∠DAB+∠BAE=∠EAC+∠BAE,
即:∠EAD=∠CAB
在△ACB 和△ADE 中:
,
∴△ACB≌△ADE(SAS),
∴BC=DE
【考点】全等三角形的判定与性质
【解析】【分析】要证两线段相等可证线段所在的三角形全等,即证△ACB≌△ADE.
20.【答案】解:本次抽样调查的总人数为 70÷35%=200(人),
则用 C:“老司机”的人数为 200×30%=60(人),
∴用 B:“洪荒之力”的人数为 200﹣(70+60+40)=30(人),
补全图形如下:
估计该校学生用得最多的网络流行语“蓝瘦香菇”的人数为 3000×35%=1050 人
【考点】扇形统计图,条形统计图
【解析】【分析】部分÷百分比=总量,总量×百分比=部分,样本中的百分比可以估计总体中
的百分比.
四.解答题
21.【答案】(1)解:原式=x2+6x+9﹣x2﹣2x=4x+9
(2)解:原式= ÷ = • =
【考点】单项式乘多项式,完全平方公式,分式的混合运算
【解析】【分析】(1)利用完全平方公式和去括号法则,合并同类项法则即可;(2)分式化
简的基本方法有通分、约分,分子分母出现多项式时看能否分解因式,便于约分.
22.【答案】(1)解:∵OA=OB,
∠ABO=∠OAB=45°,
∵CD⊥x 轴于 D,
∴∠ADC=90°,
∴∠BAD=∠ACD=45°,
∴CD=AD,
∵AC=2 ,
∴CD=AD= AC=2,
∴△ADC 的面积为 = =2
(2)解:∵OA=1,AD=2,
∴OD=1,
∵CD=2,
∴C 的坐标为(﹣1,2),
∵点 C 在反比例函数 y= 的图象上,
∴2= ,
∴k2=﹣2,
∴反比例函数的表达式为 y=﹣ ;
∵一次函数 y=k1x+b 过 B(0,1),C(﹣1,2),
∴代入得: ,
解得:b=1,k1=﹣1,
∴一次函数的表达式为 y=﹣x+1
【考点】反比例函数与一次函数的交点问题
【解析】【分析】(1)先求由 OA=OB,得∠ABO=∠OAB=45°,进而算出 CD=AD=2,最后算出
面积;(2)先求 C 坐标,利用待定系数法,把 BC 坐标代入直线解析式即可.
23.【答案】(1)解:设 M 款运动鞋每双降价 x 元,
根据题意得:1200﹣x﹣800≥800×20%,
解得:x≤240.
答:M 款运动鞋每双最多降价 240 元,才能使利润率不低于 20%
(2)解:令 y=m%,则 m%= y, m%= y,
根据题意得:[1200×(1﹣ y)﹣800]×100(1+ y)=40000,
整理得:5y2﹣3y=0,
解得:y= =60%或 y=0(不合题意,舍去),
∴m=60.
答:m 的值为 60
【考点】一元二次方程的应用,一元一次不等式的应用
【解析】【分析】(1)由“利润率不低于 20%”,根据“(售价-进价) 进价=利润率“,可列不
等式 1200﹣x﹣800≥800×20%;(2)根据“销量 单件利润“,利润达到了 40000 元,可列方
程[1200×(1﹣ 1 3 y)﹣800]×100(1+ 5 2 y)=40000,求出 m 值.
24.【答案】(1)证明:若“矩数”m=k(k+1)是 3 的倍数,则 k(k+1)是 3 的倍数,k 是正
整数,
当 k 为奇数时,k+1 是偶数,则 k(k+1)是能被 3 整除的偶数,故 k(k+1)是 6 的倍数;
当 k 为偶数时,则 k(k+1)是能被 3 整除的偶数,故 k(k+1)是 6 的倍数,
综上所述,若“矩数”m 是 3 的倍数,则 m 一定是 6 的倍数
(2)解:根据题意得 p=t(t+1),q=s(s+1),D(p,q)=t(t+1)﹣s(s+1)=30,
即 t2+t﹣s2﹣s=30,
∴(t﹣s)(t+s+1)=30,
∵t,s 是正整数,t>s,
∴t﹣s,t+s+1 是正整数,且 t+s+1>t﹣s,
∵30=1×30=2×15=3×10=5×6,
∴ 或 或 或 ,
解得: 或 或 或 ,
∵t,s 是正整数,
∴符合条件的是: 或 或 ,
∴ 或 = 或 = ,
∵ ,
∴ 的最大值是
【考点】因式分解的应用
【解析】【分析】(1)连续的两个整数必是一奇数,一偶数,可分类证明;(2)可把新定义
的规则转化为已知的规则,用已知代数式表示新运算法则,根据 30 的因数分解规则,求出
最大值.
25.【答案】(1)解:∵BD⊥AD,点 E在 AD 的延长线上,
∴∠BDE=90°,
∵BD=DE= ,
∴BE= = ,
∵BC⊥CE,
∴∠BCE=90°,
∴BC= = =2
(2)解:连接 AF,
∵CD⊥BD,DF⊥CD,
∴∠BDE=∠CDF=90°,
∴∠BDF=∠CDE,
∵CE⊥BC,
∴∠BCE=90°,
∴∠DBC=∠CED,
在△BDF 和△EDC 中,
∵ ,
∴△BDF≌△EDC(ASA),
∴DF=CD,
∴∠CFD=∠DCF=45°,
∵∠ADB=∠CDF,
∴∠ADB+∠BDF=∠CDF+∠BDF,
∴∠ADF=∠BDC,
在△ADF 和△BDC 中,
∵ ,
∴△ADF≌△BDC(SAS),
∴∠AFD=∠BCD,
∴∠AFD=45°,
∴∠AFC=∠AFD+∠CFD=90°,
∴AF⊥BC,
∴AB=AC,
∴BF=CF
【考点】全等三角形的判定与性质
【解析】【分析】利用勾股定理可求出 BE,进而求出 BC;(2)要证线段相等,可证△BDF≌
△EDC,为△ADF≌△BDC 准备条件,证出 BF=CF.
五.解答题
26.【答案】(1)解:y= x2+ x﹣ = (x+1)2﹣ ,顶点 D的坐标为(﹣
1,﹣ ),
当 y=0 时, x2+ x﹣ =0,解得 x1=﹣3,x2=1,
∴A(﹣3,0),B(1,0).
当 x=0 时,y=﹣ ,
∴C(0,﹣ ),
∴直线 AC 的解析式为 y=﹣ x﹣
(2)解:∵△CPE 得周长为 BC+CE+BE,其中 BC 的长是固定的,
∴周长取得最小值就是 BE+CE 取得最小值,
∵点 E是抛物线对称轴上一点,
∴BE=AE,
∴BE+CE=AE+CE,
∴BE+CE 的最小值是 AC,点 E 是 AC 与对称轴的交点.
∴点 E为(﹣1,﹣ ).
∵点 P 是抛物线上 x 轴下方一点,设点 P 为(t, t2+ t﹣ ).且 t2+ t
﹣ <0.
过点 P 作 QP⊥x 轴交直线 AC 于点 Q,点 Q 坐标为(t,﹣ t﹣ ).
当点 p 在对称轴左侧时,S△PCE=S△PCQ﹣S△PEQ= PQ(0﹣t)﹣ PQ(﹣1﹣t)= PQ,
当点 P 在对称轴的右侧时,S△PCE=S△PCQ+S△PEQ= PQ(0﹣t)+ PQ[t﹣(﹣1)]= PQ,
∵PQ=(﹣ t﹣ )﹣( t2+ t﹣ )=﹣ t2﹣ t,
∴S△PCE= PQ=﹣ t2﹣ t=﹣ (t+ )2+ .
当 t=﹣ 时,△PEC 的面积最大,最大值是 ,此时,点 P 的坐标为(﹣ ,﹣ )
(3)解:经过点 P 且平行于 AC 的直线 MN 的解析式为 y=﹣ x﹣ ,
当 x=0 时,y=﹣ ,即 N(0,﹣ ),当 y=0 时,x=﹣ ,即 M(﹣ ,0),
设点 D′的坐标为(﹣1,d),则 MN2=(﹣ )2+(﹣ )2= ,MD′2=[﹣ ﹣
(﹣1)]2+d2= +d2 , ND′2=(﹣1)2+(﹣ ﹣d)2=d2+ d+ .
当∠MD′N=90°时,MD′2+ND′2=MN2 , 即 +d2+d2+ d+ = ,
整理,得 4d2+7 d﹣17=0,解得 d1= ,d2= ,
当∠NMD′=90°时,MD′2=ND′2+MN2 , 即 +d2=d2+ d+ + ,
化简,得 d=﹣ ,解得 d=﹣ ,
当∠NMD′﹣90°时,ND′2=MD′2+MN2 , 即 d2+ d+ = +d2+ ,
化简,得 d= ,解得 d= ,
∴存在点 D',使得点 D',M,N 三点构成的三角形为直角三角形,D′点的坐标为(﹣1,
)(﹣1, ),(﹣1, )(﹣1 )
【考点】二次函数与一次函数的交点问题
【解析】【分析】(1)利用配方法可配成顶点式,求出顶点坐标;(2)△BCE 的周长最小,
即 CE+BE 最小,由对称法可求得点 E 在 AC 与对称轴的交点处时,△BCE 的周长最小,△PCE
面积的最大值可运用函数思想,设点 P 的横坐标为 t,其纵坐标用 t 的代数式表示,作出 x
轴垂线,把△PCE 分割为两个有竖直边的三角形,构建关于面积的函数,配成顶点式求出最
值;(3)D',M,N 三点构成的三角形为直角三角形须分类讨论:∠MD′N=90°或∠NMD′
=90°或∠NMD′﹣90°,利用勾股定理列出方程.
数学模拟试卷(一)
(全卷共四个大题,满分 150 分,考试时间 120 分钟)
注意事项:
1.试题卷上各题的答案用黑色签字笔或钢笔书写在答题卡...上,不得在试题卷 上直接作答;
2.答题前认真阅读答题卡...上的注意事项;
3.作图(包括作辅助线)请一律用黑色..的签字笔完成;
4.考试结束,由监考人员将试题卷和答题卡...一并收回.
参考公式 :抛物线
2 ( 0)y ax bx c a 的顶点坐标为
24( , )
2 4
b ac b
a a
,对称轴公式为
2
bx
a
.
一、选择题:(本大题 12 个小题,每小题 4 分,共 48 分)在每个小题的下面,都给出了代
号为 A,B,C,D 的四个答案,其中只有一个是正确的,请将答题卡...上题号右侧正确答案所
对应的方框涂黑.
1. 下列实数中最小的是( )
A. 3 B.-2 C.π D.
3
2
2.剪纸是中国传统文化艺术,下列剪纸中不是轴对称图形的是( )
A. B. C. D.
3. 据统计 2018年末中国人口总数已经达到 1390000000人,请用科学计数法表示中国 2018
年末人口数( )
A. 710139 B. 91039.1 C. 8109.13 D. 1010139.0
4. 已知 a 是整数,满足 a< 3 +2<a+1,求 a2+2a=( )
A. 15 B.16 C.24 D.35
5.已知 x,y是方程组
124
1423
yx
yx ,
的解,则 x—y的值是( )
A.1 B.2 C.3 D.4
6.如图四边形 ABCD 是圆的内接四边形. 连接 AO ,CO,已知
o118AOC ,求 ABC
( )
A. o118 B. o124
C. o121 D. o120
7.下列命题的逆命题是真命题的个数有( )
①如果 a=2,则一定有 a2=4; ②两直线平行,内错角相等;
③菱形是四条边相等的四边形; ④如果∣m∣=∣n∣,那么 m=n.
A.4 B.3 C.2 D.1
8.按如图所示的运算程序运算,当输入的 x =2 时,输出的结果是( )
A.100 B.9 C.507 D.508
9.二次函数 y=2x2-3的图象是一条抛物线,下列关于该抛物线的说法,正确的是( )
A.抛物线开口向下 B.抛物线经过点(2,3)
C.抛物线的对称轴是直线 x=1 D.抛物线与 x 轴有两个交点
10.如图,某校门口有一坡度为 1:1.875 的破面 EF,破面 EF 长为 34 米,其对面 12 米处(AE
=12 米)处有一大楼 ABCD,在破顶 F 处测得楼顶 D的仰角为 35°,则大楼高 AD 约为( )
米.
(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)
A.29.94 B.42.4 C.45.4 D.50.44
11.如右图,在平面直角坐标系中,正方形 ABCD 的边长为 5,A 的坐标为(1,4)与反比例函
数
x
ay
2
的图象恰好交于 CD 中点 E,则 a的值为( )
A. 64 B. 65 C. 68 D. 70
11 题图
10 题图
12.若数 m 使关于 x 的不等式组
4
31
2
1
xx
mx
至少有三个整数解,且使关于 x 的分式方程
4
5
12
5
23
x
m
x
x
有非负数解,则满足条件的整数 m 的值之和是( )
A. 28 B. 30 C. 32 D. 34
二、填空题:(本大题 6 个小题,每小题 4 分,共 24 分)请将每小题的答案直接填在答题卡...
中对应的横线上.
13.计算: 32019-30sin427 0o )( =______________.
14.菱形 ABCD 的对角线 AC长 8,对角线 BD 长 6,那么菱形 ABCD 的面积是______________.
15.一个不透明的盒子里装有四个相同大小的乒乓球,其中每个乒乓球上分别标有 1,2,3,
4四个不同的数字,每次摸乒乓球前先将盒子里的球摇匀,任意摸出一个乒乓球记下数字后
再放回盒子,那么两次摸出的乒乓球上数字之和是 4的概率为____________.
16.如图,Rt△ABC 中,∠ACB=90°,AB=17,BC=8,点 EF 分别在 AB,AC 上,将点 A
沿 EF 折叠,点 A 落在△ABC 内的点 D 处,且△BCD 为等腰直角三角形,∠BDC=90°,AF
= .
17. 一天早晨,小明从家出发匀速步行到学校,小明出发一段时间后,他的妈妈发现小明忘
带了数学作业,于是立即骑自行车沿小明行进的路线,匀速去追小明.妈妈追上小明将数学
作业交给他,小明继续以原速度步行前往学校,妈妈赶着去上班,立即沿原路线返回家里,
速度提升为原速度的
4
5
倍,妈妈和小明之间的距离为 y(米)与小明从家出发后步行的时间
x(分)之间的关系如图所示(妈妈交数学作业给小明的时间忽略不计). 当妈妈刚回到家
时,小明离学校的距离为______________米.
18. 某班主任为了奖励该班评选出来的文明学生、三好学生、优秀干部,决定购买 A、B、C
三种不同奖品,甲商店给出三种奖品的单价分别为 2 元、3 元、4 元,若购买这三种奖品需
要花 49 元,乙商店给出三种奖品的价格分别为 2.5 元、1.5 元、3 元,结果只花了 40 元就
买下了这批奖品,那么 A 种奖品最多可以买 件.
三、解答题:(本大题 7 个小题,每小题 10 分,共 70 分)解答时每小题必须给出必要的演
算过程或推理步骤,画出必要的图形,请将解答过程书写在答题卡...中对应的位置上.
16 题图
17 题图
19. 计算:(1)(m-2n)2
-2n(n-2m); (2)
1
42
1 2
22
a
aaa
a
aa
.
20.如图,在△ABC 中,∠ACB=90°,∠ACB 的平分线交 AB 于点 D,点 E 是边 BC 上一点,
连接 DE,∠CED=∠CAD.
(1)求证:△ACD≌△ECD;
(2)当∠B=35°时,求∠BDE 的度数.
21. 2019 年 3 月 15 日,我国两会落下帷幕. 13 天时间里,来自各地的 5000 余名代表委员
聚于国家政治中心,共议国家发展大计.某校初三、1 班张老师为了了解同学们对两会知识
的知晓情况,进行了一次小测试,测试满分 100 分.其中 A 组同学的测试成绩分别为:91,
91 , 86,93,85,89,89,88,87,91 ; B 组 同 学 的 测 试 成 绩 分 别 为 :
88,97,88,85,86,94,84,83,98,87.
根据以上数据,回答下列问题:
(1)完成下表:
组别 平均数 中位数 众数 方差
A 组 89 89
B 组 89 88 26.2
(2)张老师将 B 组同学的测试成绩分成四组并绘制成如
下条形统计图,请补全:
(3)根据以上分析,你认为 组(填 A 或 B)的同学
对今年两会知识的知晓情况更好一些,请写出你这样判断
的理由
(至少
写两条).
21 题图
20 题图
22.王小小同学学习了函数后,想利用学习函数的经验来研究函数 y1=
3.
2
3
3,
x
x
xx
的性
质.请你跟王小小一起完成研究任务:
(1)完成列表的任务;
x … -2 -1 0 1 2 3 4 5 6 …
y … …
(2)在图中平面直角坐标系内作出函数图象;
(3)观察图象,写出函数的一条性质 ;
(4)对于函数 y2= 2
1
x+b,若 y2的图象与 y1的
图象有两个不同的交点,由图象可得 b的取值范
围是 .
23. 2019 年 2 月 28 日,荣昌国家高新技术产业开发区成立一周年.3 月 2 日,某校老师带数
学活动小组到某公司调查一年来该公司甲、乙两种产品的生产经营情况.
(1)据了解,该公司生产一件甲产品所需成本比乙少 5 元,当天上午一个车间生产出的甲、
乙产品数量相同,且甲产品共耗成本 2700 元,乙产品共耗成本 3000 元.该公司生产甲、乙
产品所耗成本每件需多少元?
(2)该企业销售主管告诉同学们,甲、乙产品分别按每件 70 元和 80 元的价格外销,今年
2月分别销售了 600 件、800 件.3 月准备重新调价销售,据经验甲产品每涨一元,月销售量
少将减少 10 件,企业准备将甲产品提价 m 元/件进行销售;乙产品销售价格准备提高
4
5
m%,
这样乙的销量将减少
8
5
m%.这样一来,3 月该公司这两种产品的利润将比 2月多 7040 元.求
m 的值.
22 题图
24. 平行四边形 ABCD 中,∠A=45°,连接 BD.
(1)如图 1,若 BD= 2 AD,AD=6.求平行四边形 ABCD 的面积;
(2)如图 2,若对角线 BD⊥AD,∠BAD 的平分线交 BD 于点 E,点 F 是 CD 上一点,且 CF
=BC,连接 BF.求证:BE= 2 DF.
25.阅读材料:将 ba 2 化简,使根号内不含根号,如果你能找到两个数 m,n,使 m2
+n2
=a 且 mn= b ,则将 a±2 b 将变成 m2
+n2
±2mn,即变成(m±n)2
开方,从而使得
ba 2 化简.例如,5±2 6 =3+2±2 6 = 23)( + 22 ±2 2 × 3 =
223 ,所以 625 = 223 = 3 ± 2 .
请仿照上例解下列问题:
(1)化简 526 ;(2)化简 3
6
1-
3
1
.
24 题图 1 24 题图 2
四、解答题:(本大题 1 个小题,共 8 分)解答时每小题必须给出必要的演算过程或推理步
骤,画出必要的图形,请将解答过程书写在答题卡...中对应的位置上.
26.已知抛物线 y=
9
3
x2+
3
2
x- 3 与 x 轴交于 A,B 两点(点 A 在点 B 左侧),与 y 轴交于
点 C,连接 AC,并作直线 BC.
(1)如图 1,过点 B 作 BD∥AC 交 y 轴于点 D,点 P 是 AC 下方的抛物线上一动点,当△PAD
面积最大时,在直线 BC 上有两动点 M,N(点 M 在点 N 的下方),且 MN= 2 ,x 轴上一
动点 Q,求 PM+MN+NQ+
10
10
QA 的最小值.
(2)将△OBC 绕点 O 逆时针旋转 180°,直线 CB 在旋转过程中与 x 轴交于点 E,与直线 AC
交于点 F,若△EAF 为等腰三角形时,直接写出点 E的坐标..
26 题图 1
26 题图 2
26 题备用图
数学模拟试卷(二)
(全卷共四个大题,满分 150 分,考试时间 120 分钟)
注意事项:
1.试题卷上各题的答案用黑色签字笔或钢笔书写在答题卡...上,不得在试题卷 上直接作答;
2.答题前认真阅读答题卡...上的注意事项;
3.作图(包括作辅助线)请一律用黑色..的签字笔完成;
4.考试结束,由监考人员将试题卷和答题卡...一并收回.
参考公式 :抛物线
2 ( 0)y ax bx c a 的顶点坐标为
24( , )
2 4
b ac b
a a
,对称轴公式为
2
bx
a
.
一、选择题:(本大题 12 个小题,每小题 4 分,共 48 分)在每个小题的下面,都给出了代
号为 A,B,C,D 的四个答案,其中只有一个是正确的,请将答题卡...上题号右侧正确答
案所对应的方框涂黑.
1.﹣2019 的相反数是( )
A.﹣2019 B.2019 C. D.
2.如图图形中,是中心对称图形的是( )
A. B. C. D.
3. 计算的结果是( )
A.25x5y2 B.25x6y2 C.﹣5x3y2 D.﹣10x6y2
4.下列调查中,适宜采用全面调查(普查)方式的是( )
A.调查一批新型节能灯泡的使用寿命 B.调查荣昌区中小学生的课外阅读时间
C.调查我区初中学生的视力情况 D.调查“神州十一号”飞船零部件的安全性能
5.要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为 5cm,6cm 和 9cm,
另一个三角形的最短边长为 2.5cm,则它的最长边为( )
A.3cm B.4cm C.4.5cm D.5cm
6.下列命题是真命题的是( )
A.如果|a|=|b|,那么 a=b B.平行四边形对角线相等
C.两直线平行,同旁内角互补 D.如果 a>b,那么 a2
>b2
7.估计 182 的值应在( )
1
2019
1
2019
3 25( ) x y
A.3 和 4 之间 B.4 和 5 之间 C.5 和 6 之间 D.6 和 7 之间
8.按如图所示的运算程序,
能使运算输出的结果为 7的是( )
A. 32 yx , B. 32 yx , C. 38 yx , D. 6 5x y ,
9.如图,在矩形 ABCD 中,AB=4,BC=6,点 E 是 AB 中点,在 AD 上取一点 G,以点 G 为
圆心,GD 的长为半径作圆,该圆与 BC 边相切于点 F,连接 DE,EF,则图中阴影部分面积
为( )
A.3π B.4π C.2π+6 D.5π+2
10.重庆朝天门码头位于置庆市油中半岛的嘉陵江与长江交汇处,是重庆最古老的码头.如
图,小王在码头某点 E 处测得朝天门广场上的某高楼 AB 的顶端 A 的仰角为 45°,接着他沿
着坡度为 1:2.4 的斜坡 EC 走了 26 米到达坡顶 C 处,到 C 处后继续朝高楼 AB 的方向前行
16 米到 D 处,在 D 处测得 A 的仰角为 74°,则此时小王距高楼的距离 BD 的为( )米(结
果精确到 1米,参考数据:sin74°≈0.96,cos74°≈0.28,tan74°≈3.49)
A.12 B.13 C.15 D.16
9 题图 10 题图 11 题图
11.已知,如图 Rt△OAB 是等腰直角三角形,AD 为底边 OB 边上的高,C 为 AD 中点,双曲
线经过点 C,交 OA,AB 于 E,F.连接 E,F,则△AFE 的面积为( )
A. B. C. D.
12.若数 m 使关于 x 的分式方程
6 1
2
a
x x
的解为正整数,且关于 x 的不等式组
,有解且最多有 8 个整数解,则满足条件的所有整数 a 的值之和是( )
A.3 B.12 C.0 D.4
二、填空题:(本大题 6 个小题,每小题 4 分,共 24 分)请将每小题的答案直接填在答题卡...
中对应的横线上.
13.(
1
3
)
2
-( 3 - )
0
= .
4 2 2 2 2 2 5 2 2 2 2 1
5 35
3
2
2
x x
0a x
14.一个不透明的容器中装有大小、质地都相同的小球,球面上分别标有 3、1、-2,均匀搅
拌后任意摸出一个球(摸出后不放回),记下数字作为 P 点的横坐标,再从余下的两个小球
中任意摸出一个小球,记下数字作为点 P 的纵坐标,则点 P 落在第二象限的概率
为 .
15.如图,AB 是⊙O 的直径,DC 与⊙O 相切于点 C,若∠D=30°,OA=2,则 CD= .
16.如图,点是矩形 ABCD 的边 CD 上一点,把△ADE 沿 AE 对折,使点 D 恰好落在 BC 边上
的 F 点处.已知折痕 AE=10 10 ,且 CE:CF=3:4,那么该矩形的周长为 .
17.在一条笔直的公路上顺次有 A,B,C 三地,甲车从 B 地出发往 A 地匀速行驶,到达
A 地后停止.在甲车出发的同时,乙车也从 B 地出发往 A 地匀速行驶,到达 A 地停留 1
小时后,调头按原速向 C 地行驶.若 AB 两地相距 300 千米,在两车行驶的过程中,甲、
乙两车之间的距离 y(千米)与乙车行驶时间 x(小时)之间的函数图象如图所示,则在两
车出发后经过 小时相遇.
15 题图 16 题图 17 题图
18.我区某校第二课堂活动开展的如火如荼,为了解同学们对体育运动项目的喜好程度,某
班对“足球”、“篮球”、“羽毛球”、“乒乓球”喜好进行投票(每人限投一票).喜好
“足球”的人数比喜好“羽毛球”的人数多 8 人,喜好“篮球”的人数是喜好“足球”的整
数倍;喜好“篮球”和“足球”的人数是喜好“羽毛球”和“乒乓球”的 5 倍,喜欢“乒乓
球”和“篮球”的人数之和比喜欢“足球”和“羽毛球”的人数多 24 人,则这个班级共有
人.
三、解答题:(本大题 7 个小题,每小题 10 分,共 70 分)解答时每小题必须给出必要的演
算过程或推理步骤,画出必要的图形,请将解答过程书写在答题卡...中对应的位置上.
19.化简(1) 23 3 3( )( ) ( ) x y x y x y ; (2) 2
2 1 21
1 2 1
( )
x xx+
x x x
20.如图,在△ABC 中,∠ACB=90°,AD 平分∠CAB 交 BC 于 D
点,过 D 点作 DE⊥AB 于点 E.
(1)求证: △ACD≌△AED;
(2)若 AC=7,AB=25,求线段 CD 的长.
21.距离中考体考时间越来越近,某校想了解初三年级 2400 名学
生周末在家体育锻炼的情况,在初三年级随机抽查了 20 名男生和 20 名女生周末每天在家锻
炼的时间情况.
(一)收集数据(单位:分)
男生: 60 70 40 45 20 120 80 50 45 40
85 90 90 30 90 50 90 50 70 100
女生:100 30 80 70 60 75 90 40 75 60
75 75 90 70 80 50 80 100 90 120
(二)整理、描述数据:(表一)
时间(x)
男生 2 8 8 2
女生 1 4 a 3
(表格二)两组数据的极差、平均数、中位数、众数
极差 平均数 中位数 众数
男生 100 65.75 b c
女生 90 75.5 75 75
(三)分析、应用数据:
(1)请将上面两个表格补充完整:
a= , b= , c= .
(2)请根据抽样调查的数据估计该校初三年级周末每天锻炼时间在 100 分钟以上(含 100
分钟)的同学大约有多少人?
(3)王老师看了表格数据后认为初三年级的女生周末锻炼坚持得比男生好,请你根据统计
数据,写出支持王老师观点的理由.
22.某校数学兴趣小组根据学习函数的经验,对函数 y=
2
1
∣x∣-1 的图像和性质进行了探
究,探究过程如下:
x … -4 -3 -2 -1 0 1 2 3 4 …
y … 1 0.5 m -0.5 -1 -0.5 0 n 1 …
(1)自变量 x 的取值范围是全体实数,x 与 y 的几组对应值如下表,其中 m= ,
n= ;在平面直角坐标系 xoy 中,描出了上表中各对对应值为坐标的点,根据描出
的点画出该函数的图像;
(2)结合函数图象,请写出函数 y=
2
1
∣x∣-1 的一条性质;
(3)直线 y=
6
1
x+
3
5
与函数 y=
2
1
∣x∣-1 的图像所围成的三角形的面积.
23.某文具店第一次购进甲、乙两种文具.购进甲文具花费 3200 元,购进乙文具花费 2400
元,其中甲文具数量是乙文具数量的 2 倍,已知购进一个甲文具比购进一个乙文具多花
20 元.
(1)求购进一个甲文具和一个乙文具各需多少元?
(2)由于畅销,该店决定第二次购进甲、乙两种文具,恰逢两种文具进价进行调整,甲文
具进价比第一次提高 a元(a>0),乙文具按第一次进价 9 折购进.如果第二次购进甲文
具数量比第一次少 2a个,第二次购进乙文具比第一次多 个,则第二次购进甲、乙两
种文具的总费用比第一次少 320 元.求 a的值.
24.菱形ABCD中, AE分∠DAB为∠DAE与∠BAE,且∠BAE=
7
3
∠DAE,AE交对角线BD于F,交
BC于E,过点A作AG⊥CD于G,交BD于H,且∠BDC=15°.
2
a
(1)求∠AEC的度数;
(2)求证:BF=
2
1
BH+FA. .
25.阅读材料:
材料(一):二次根式的运算可充分利用有理数的运算律及乘法公式.例如:
( a ± b )
2
=a±2 ab +b;
拓展:( a+ b + c)2
=〔 a +( b + c)〕2
=a+2 a ( b + c )+b+2 bc
+c=a+b+c+2 ab+2 ac+2 bc ;
材料(二):法国著名数学家费马在给数学朋友的一封信中提出关于三角形的一个有趣问题,
“在三角形所在平面上求一个点,使该点在到三角形三个顶点的距离之和最小”.具体方法:
如图 1,将△ACP 绕着点 C 顺时针旋转 60°得到△A´CP´,则△ACP≌△A´CP´,CP=CP´,AP=A
´P´,∠PCP´=∠ACA´=60°,故△PCP´是等边三角形,由 PA+PB+PC=A´P´+PB+PP´≥A´B.故
当 B,P,P´,A´四点共线时,PA+PB+PC 有最小值,最小值为 A´B.
(1)应用材料(一),计算: , ;
(2)应用材料(一)、(二)解决问题:如图 2,已知△ABC 中,∠ABC=90°,AB=BC= ,
P 是△ABC 内一点.求 PA+PB+PC 的最小值.
图 1 图 2
四、解答题:(本大题 1 个小题,共 8 分)解答时每小题必须给出必要的演算过程或推理步
骤,画出必要的图形,请将解答过程书写在答题卡...中对应的位置上.
26.已知抛物线 y=-x2+2x+3 与 x 轴交于 A,B 两点(点 A 在点 B 的左侧),与 y 轴交于
2( 2 1) _____ 2( 5 3 2) __________
2
点 C.
(1)如图 1,点 P 为线段 BC 上方抛物线上的任意一点,点 D 是 x 轴正半轴上一点,且
OD= OC,当三角形 PCD 面积最大时,在 y 轴上取一点 M,x 轴上取一点 N,求
PM+MN+ NB 的最小值;
(2)如图 2,将△AOC 绕点 O 顺时针旋转至△A1OC1的位置,点 A,C 的对应点分别为
A1,C1,且点 A1落在线段 AC 上,再将△A1OC1沿 y 轴平移得△A2O1C2,其中直线 O1C2与
x轴交于点 K,点 T 是抛物线对称轴上的动点,连接 KT,O1T,△O1KT 能否成为以 O1K 为
直角边的等腰直角三角形?若能,请直接写出所有符合条件的点 T 的坐标;若不能,请
说明理由.
图 1 图 2
专题突破:动点函数图象
动点函数图象和立体图形的展开折叠是初中数学和高中数学的重要接轨点之一,是北京
中考选择压轴题的热点,近年来立体图形的展开与折叠只在 2019 年出现,更多的是考查动
点函数图象.
2019—2019 年北京中考知识点对比
题型
年份
2019 2019 2019 2019 2019
题型
动点生
成的函
数图象
由函数
图象判
断运动
情况
动点生
成的函
数图象
由函数
图象判
断运动
情况
由函数
图象判
断运动
情况
1.[2019·北京] 一个寻宝游戏的寻宝通道如图 Z2-1 所示,通道由在同一平面内的 AB,
1
3 1
2
BC,CA,OA,OB,OC组成.为记录寻宝者的行进路线,在 BC的中点 M处放置了一台定
位仪器,设寻宝者行进的时间为 x,寻宝者与定位仪器之间的距离为 y,若寻宝者匀速行进,
且表示 y与 x的函数关系的图象大致如图②所示,则寻宝者的行进路线可能为( )
图 Z2-1
A.A→O→B B.B→A→C
C.B→O→C D.C→B→O
2.[2019·北京] 已知点 A为某封闭图形边界上的一定点,动点 P从点 A出发,沿其边
界顺时针匀速运动一周,设点 P运动的时间为 x,线段 AP的长为 y,表示 y与 x的函数关
系的图象大致如图 Z2-2 所示,则该封闭图形可能是图 Z2-3 中的( )
图 Z2-2
图 Z2-3
3.[2019·北京] 如图 Z2-4,点 P是以 O为圆心,AB为直径的半圆上的动点,AB=2,
设弦 AP的长为 x,△APO的面积为 y,则下列图象中,能表示 y与 x的函数关系的图象大
致是图 Z2-5 中的( )
图 Z2-4
图 Z2-5
4.[2019·北京] 小翔在如图 Z2-6①所示的场地上匀速跑步,他从点 A出发,沿箭头
所示方向经过点 B跑到点 C,共用时 30 秒,他的教练选择了一个固定的位置观察小翔的跑
步过程,设小翔跑步的时间为 t(单位:秒),他与教练的距离为 y(单位:米),表示 y与 t的
函数关系的图象大致如图②所示,则这个固定位置可能是图①中的( )
图 Z2-6
A.点 M B.点 NC.点 P D.点 Q
5.[2019·北京] 如图 Z2-7,在 Rt△ABC中,∠ACB=90°,∠BAC=30°,AB=2,
D是 AB边上的一个动点(不与点 A,B重合),过点 D作 CD的垂线交射线 CA于点 E.设 AD
=x,CE=y,则图 Z2-8 的图象中,能表示 y与 x的函数关系的图象大致是( )
图 Z2-7
图 Z2-8
6.[2019·北京] 美术课上,老师要求同学们将图 Z2-9 所示的白纸只沿虚线剪开,用
裁开的纸片和白纸上的阴影部分围成一个立体模型,然后放在桌面上,图 Z2-10 中的四个
示意图中,只有一个符合上述要求,那么这个示意图是( )
图 Z2-9
图 Z2-10
一、动点生成函数图象
1.[2019·海淀二模] 如图 Z2-11 所示,点 Q表示蜜蜂,它从点 P出发,按照着箭头
所示的方向沿 P→A→B→P→C→D→P的路径匀速飞行,此飞行路径是一个以直线 l为对称
轴的轴对称图形,在直线 l上的点O处(点O与点P不重合)利用仪器测量了∠POQ的大小.设
蜜蜂飞行时间为 x,∠POQ的大小为 y,则下列图象中,能表示 y与 x的函数关系的图象大
致是图 Z2-12 中的( )
图 Z2-11
图 Z2-12
2.[2019·东城一模] 如图 Z2-13①,△ABC和△DEF都是等腰直角三角形,其中∠C
=∠EDF=90°,点 A与点 D重合,点 E在 AB上,AB=4,DE=2.如图②,△ABC保持不
动,△DEF沿着线段 AB从点 A向点 B移动,当点 D与点 B重合时停止移动.设 AD=x,
△DEF与△ABC重叠部分的面积为 S,则 S关于 x的函数图象大致是图 Z2-14 中的( )
图 Z2-13
图 Z2-14
3.[2019·西城一模] 如图 Z2-15,过半径为 6 的⊙O上一点 A作⊙O的切线 l,P为
⊙O上的一个动点,作 PH⊥l于点 H,连接 PA.如果 PA=x,AH=y,那么图 Z2-16 的图
象中,能大致表示 y与 x的函数关系的是( )
图 Z2-15
图 Z2-16
4.[2019·西城一模] 如图 Z2-17,在平面直角坐标系 xOy中,以点 A(2,3)为顶点任
作一直角∠PAQ,使其两边分别与 x轴、y轴的正半轴交于点 P,Q,连接 PQ,过点 A作
AH⊥PQ于点 H.设点 P的横坐标为 x,AH的长为 y,则下列图象中,能表示 y与 x函数关
系的图象大致是图 Z2-18 中的( )
图 Z2-17
图 Z2-18
5.[2019·朝阳二模] 如图 Z2-19,矩形 ABCD中,E为 AD的中点,点 F为 BC上的
动点(不与 B,C重合).连接 EF,以 EF为直径的圆分别交 BE,CE于点 G,H.设 BF的长
度为 x,弦 FG与 FH的长度和为 y,则图 Z2-20 中的图象中,能表示 y与 x之间的函数关
系的图象大致是( )
图 Z2-19
图 Z2-20
二、由函数图象判断运动情况
6.[2019·海淀一模] 小明在书上看到了一个实验:一个盛了水的圆柱形容器内,有一
个顶端拴了一根细绳的实心铁球,将铁球从水面下沿竖直方向慢慢地匀速向上拉动.小明将
此实验实行了改进,他把实心铁球换成了材质相同的别的物体,记录实验时间 t以及容器内
水面的高度 h,并画出表示 h与 t的函数关系的大致图象,如图 Z2-21 所示.小明选择的
物体可能是( )
图 Z2-21
图 Z2-22
7.[2019·燕山一模] 李阿姨每天早晨从家慢跑到小区公园,锻炼一阵后,再慢跑回家.表
示李阿姨离开家的距离 y(单位:米)与时间 t(单位:分)的函数关系的图象大致如图 Z2-23
所示,则李阿姨跑步的路线可能是(用 P点表示李阿姨家的位置)( )
图 Z2-23
图 Z2-24
8.[2019·海淀二模] 如图 Z2-25①,AB是半圆 O的直径,正方形 OPNM的对角线 ON
与 AB垂直且相等,Q是 OP的中点.一只机器甲虫从点 A出发匀速爬行,它先沿直径爬到
点 B,再沿半圆爬回到点 A,一台微型记录仪记录了甲虫的爬行过程.设甲虫爬行的时间为
t,甲虫与微型记录仪之间的距离为 y,表示 y与 t的函数关系的图象如图②所示,那么微型
记录仪可能位于图①中的( )
图 Z2-25
A.点 M B.点 N C.点 P D.点 Q
9.[2019·海淀二模] 如图 Z2-26①,在矩形 ABCD中,ABm时,y=15+2(m-10)+3(x-m)=3x-m-5.
∴y=
1.5x 0≤x≤10,
2x-5 10m.
(3)当 40≤m≤50 时,y=2×40-5=75(元),满足.
当 20≤m<40 时,y=3×40-m-5=115-m,
则 70≤115-m≤90,∴25≤m≤45,即 25≤m≤40.
综上得,25≤m≤50.
3.潼南绿色无公害蔬菜基地有甲、乙两种植户,他们种植了 A,B两类蔬菜,两种
植户种植的两类蔬菜的种植面积与总收入如下表:
种植户 种植 A类蔬菜面积(单位:亩) 种植 B类蔬菜面积(单位:亩) 总收入(单位:元)
甲 3 1 12 500
乙 2 3 16 500
说明:不同种植户种植的同类蔬菜每亩的平均收入相等;亩为土地面积单位.
(1)求 A,B两类蔬菜每亩的平均收入各是多少元;
(2)某种植户准备租 20 亩地用来种植 A,B两类蔬菜,为了使总收入不低于 63 000 元,
且种植 A类蔬菜的面积多于种植 B类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植
户所有的租地方案.
解:(1)设 A,B两类蔬菜每亩平均收入分别是 x元,y元.
由题意,得
3x+y=12 500,
2x+3y=16 500.
解得
x=3 000,
y=3 500.
答:A,B两类蔬菜每亩平均收入分别是 3 000 元,3 500 元.
(2)设用来种植 A类蔬菜的面积为 a亩,则用来种植 B类蔬菜的面积为(20-a)亩.
由题意,得
3 000a+3 50020-a≥63 000,
a>20-a.
解得 10<a≤14.
∵a取整数,为:11,12,13,14.
∴租地方案为:
类别 种植面积(亩)
A 11 12 13 14
B 9 8 7 6
4.某学校计划将校园内形状为锐角△ABC 的空地(如图)进行改造,将它分割成△AHG、△
BHE、△CGF 和矩形 EFGH 四部分,且矩形 EFGH 作为停车场,经测量 BC=120m,高 AD=80m,
(1)若学校计划在△AHG 上种草,在△BHE、△CGF 上都种花,如何设计矩形的长、
宽,使得种草的面积与种花的面积相等?
(2)若种草的投资是每平方米 6 元,种花的投资是每平方米 10 元,停车场铺地砖投资
是每平方米 4 元,又如何设计矩形的长、宽,使得△ABC 空地改造投资最小?最小为多少?
解、(1)设 FG=x 米,则 AK=(80-x)米
由△AHG∽△ABCBC=120,AD=80 可得:
80
80
120
xHG
∴ xHG
2
3120
BE+FC=120- )( x
2
3120 = x
2
3
∴ xxxx ·
2
3
2
180·
2
3120 ·
2
1
)()( 解得 x=40
∴当 FG 的长为 40 米时,种草的面积和种花的面积相等。
(2)设改造后的总投资为 W 元
W= 2880024064·)
2
3120(10··
2
3
2
16·80·
2
3120 ·
2
1 2 xxxxxxxx )()( =6(x
-20)2+26400
∴当 x=20 时,W 最小=36400
答:当矩形 EFGH 的边 FG长为 20 米时,空地改造的总投资最小,最小值为 26400 元。
5.我州鼓苦荞茶、青花椒、野生蘑菇,为了让这些珍宝走出大山,走向世界,州政府决定组
织 21 辆汽车装运这三种土特产共 120 吨,参加全国农产品博览会.现有 A 型、B 型、C 型三
种汽车可供选择.已知每种型号汽车可同时装运 2 种土特产,且每辆车必须装满.根据下表信
息,解答问题.
苦荞茶 青花椒 野生蘑菇
每辆汽车运载量(吨)
A 型 2 2
B 型 4 2
C 型 1 6
(1)设 A 型汽车安排 x辆,B 型汽车安排 y辆,求 y与 x之间的函数关系式.
(2)如果三种型号的汽车都不少于 4 辆,车辆安排有几种方案?并写出每种方案.
(3)为节约运费,应采用(2)中哪种方案?并求出最少运费.
解:(1)法①根据题意得
4 6 7 21 120x y x y
化简得: 3 27y x
(2)由
4
4
21 4
x
y
x y
得
4
3 27 4
21 3 27 4
x
x
x x
,解得
25 7
3
x
.
∵ x为正整数,∴ 5,6,7x .故车辆安排有三种方案,即:
方案一: A型车5辆, B型车12辆,C型车 4 辆
方案二: A型车6 辆, B型车9辆,C型车6 辆
方案三: A型车7辆, B型车 6 辆,C型车8辆
(3)设总运费为W 元,则
1500 1800 3 27 2000 21 3 27W x x x x
100 36600x
∵W 随 x的增大而增大,且 5,6,7x
∴当 5x 时,
37100W 最小 元
答:为节约运费,应采用 ⑵中方案一,最少运费为 37100 元。
6.为创建“国家卫生城市”,进一步优化市中心城区的环境,德州市政府拟对部分路段的人行
道地砖、花池、排水管道等公用设施全面更新改造,根据市政建设的需要,须在 60 天内完
成工程.现在甲、乙两个工程队有能力承包这个工程.经调查知道:乙队单独完成此项工程
车型 A B C
每辆车运费(元) 1500 1800 2000
特产
车型
的时间比甲队单独完成多用 25 天,甲、乙两队合作完成工程需要 30 天,甲队每天的工程费
用 2500 元,乙队每天的工程费用 2000 元.
(1)甲、乙两个工程队单独完成各需多少天?
(2)请你设计一种符合要求的施工方案,并求出所需的工程费用.
解:(1)设甲工程队单独完成该工程需 x 天,则乙工程队单独完成该工程需(x+25)天.
根据题意得:
30 30 1
5x x
+
+2 .
方程两边同乘以 x(x+25),得 30(x+25)+30x=x(x+25),即 x2﹣35x﹣750=0.解之,得 x1=50,
x2=﹣15.
经检验,x1=50,x2=﹣15 都是原方程的解.
但 x2=﹣15 不符合题意,应舍去.∴当 x=50 时,x+25=75.
答:甲工程队单独完成该工程需 50 天,则乙工程队单独完成该工程需 75 天.
(2)此问题只要设计出符合条件的一种方案即可.
方案一:由甲工程队单独完成. 所需费用为:2500×50=125000(元).
方案二:由甲乙两队合作完成.所需费用为:(2500+2000)×30=135000(元).
7. “五一”期间,为了满足广大人民的消费需求,某商店计划用 160000 元购进一批家电,
这批家电的进价和售价如下表:
类别 彩电 冰箱 洗衣机
进价 2000 1600 1000
售价 2200 1800 1100
(1)、若全部资金用来购买彩电和洗衣机共 100 台,问商店可以购买彩电和洗衣机各多少台?
(2)、若在现有资金 160000 元允许的范围内,购买上表中三类家电共 100 台,其中彩电台数
和冰箱台数相同,且购买洗衣机的台数不超过购买彩电的台数,请你算一算有几种进货方
案?哪种进货方案能使商店销售完这批家电后获得的利润最大?并求出最大利润。(利润=
售价-进价)
解:(1)设商店购买彩电 x 台,则购买洗衣机(100﹣x)台.
由题意,得 2000x+1000(100﹣x)=160000,解得 x=60,则 100﹣x=40(台),
所以,商店可以购买彩电 60 台,洗衣机 40 台.
(2)设购买彩电和冰箱各 a 台,则购买洗衣机为(100﹣2a)台.
根据题意,得
2000 1600 1000(100-2 ) 160000
100 2
a a a
a a
解得
5.37
3
133 a
.
因为 a是整数,所以 a=34、35、36、37.
因此,共有四种进货方案.
设商店销售完毕后获得的利润为 w 元,
则 w=(2200﹣2000)a+(1800﹣1600)a+(1100﹣1000)(100﹣2a)=200a+10000,
∵200>0,∴w 随 a 的增大而增大,
∴当 a=37 时,
W最大值 =200×37+10000=17400,
所以,商店获得的最大利润为 17400 元.
8.某商场经营某种品牌的童装,购进时的单价是 60 元.根据市场调查,在一段时间内,销
售单价是 80 元时,销售量是 200 件,而销售单价每降低 1 元,就可多售出 20 件.
(1)写出销售量 y 件与销售单价 x 元之间的函数关系式;
(2)写出销售该品牌童装获得的利润 w 元与销售单价 x 元之间的函数关系式;
(3)若童装厂规定该品牌童装销售单价不低于 76 元,且商场要完成不少于 240 件的销售任
务,则商场销售该品牌童装获得的最大利润是多少?
解:(1)根据题意得,y=200+(80﹣x)×20=﹣20x+1800,
所以销售量 y 件与销售单价 x 元之间的函数关系式为 y=﹣20x+1800;
(2)W=(x﹣60)y=(x﹣60)(﹣20x+1800)=﹣20x2+3000x﹣108000,
所以销售该品牌童装获得的利润 w 元与销售单价 x 元之间的函数关系式 y=﹣20x2+3000x﹣
108000;
(3)根据题意得,﹣20x+1800≥240, x≥76, ∴76≤x≤78,
w=﹣20x2+3000x﹣108000,
对称轴为 x=﹣
3000
2 ( 20) =75,a=﹣20<0,
∴当 76≤x≤78 时,W 随 x 的增大而减小,
∴x=76 时,W 有最大值,最大值=(76﹣60)(﹣20×76+1800)=4480(元).
所以商场销售该品牌童装获得的最大利润是 4480 元.
9.在眉山市开展城乡综合治理的活动中,需要将 A、B、C 三地的垃圾 50 立方米、40 立方米、
50 立方米全部运往垃圾处理场 D、E两地进行处理.已知运往 D 地的数量比运往 E 地的数量
的 2 倍少 10 立方米.
(1)求运往两地的数量各是多少立方米?
(2)若 A 地运往 D 地 a 立方米(a 为整数),B 地运往 D 地 30 立方米,C 地运往 D 地的数
量小于 A 地运往 D地的 2 倍.其余全部运往 E 地,且 C 地运往 E 地不超过 12 立方米,则 A、
C 两地运往 D、E两地哪几种方案?
(3)已知从 A、B、C 三地把垃圾运往 D、E两地处理所需费用如下表:
A 地 B 地 C 地
运往 D 地(元/立方米) 22 20 20
运往 E 地(元/立方米) 20 22 21
在(2)的条件下,请说明哪种方案的总费用最少?
解:(1)设运往 E地 x立方米,由题意得,x+2x﹣10=140,解得:x=50,∴2x﹣10=90,
答:共运往 D 地 90 立方米,运往 E地 50 立方米;
(2)由题意可得,
12)30(9050
2)30(90
a
aA
,解得:20<a≤22,
∵a 是整数,∴a=21 或 22,∴有如下两种方案:
第一种:A 地运往 D 地 21 立方米,运往 E 地 29 立方米;C 地运往 D 地 39 立方米,运往 E
地 11 立方米;
第二种:A 地运往 D 地 22 立方米,运往 E 地 28 立方米;C 地运往 D 地 38 立方米,运往 E
地 12 立方米;
(3)第一种方案共需费用:22×21+20×29+39×20+11×21=2053(元),
第二种方案共需费用:22×22+28×20+38×20+12×21=2056(元),
所以,第一种方案的总费用最少.
10.我市化工园区一化工厂,组织 20 辆汽车装运 A、B、C 三种化学物资共 200 吨到某地.按
计划 20 辆汽车都要装运,每辆汽车只能装运同一种物资且必须装满.请结合表中提供的信
息,解答下列问题:
(1)设装运 A 种物资的车辆数为 x,装运 B 种物资的车辆数为 y.求 y 与 x 的函数关系式;
(2)如果装运 A 种物资的车辆数不少于 5 辆,装运 B 种物资的车辆数不少于 4 辆,那么车
辆的安排有几种方案?并写出每种安排方案;
(3)在(2)的条件下,若要求总运费最少,应采用哪种安排方案?请求出最少总运费.
物资种类 A B C
每辆汽车运载量(吨) 12 10 8
每吨所需运费(元/吨) 24
0
32
0
20
0
解:(1)根据题意,得:12x+10y+8(20﹣x﹣y)=200,12x+10y+160﹣8x﹣8y=2002x+y=20,
∴y=20﹣2x,
(2)根据题意,得:
5
20 2 4
x
x
≥
≥
解之得:5≤x≤8
∵x 取正整数,∴x=5,6,7,8,
∴共有 4 种方案,即
A B C
方案一 5 10 5
方案二 6 8 6
方案三 7 6 7
方案四 8 4 8
(3)设总运费为 M 元,
则 M=12×240x+10×320(20﹣2x)+8×200(20﹣x+2x﹣20)
即:M=﹣1920x+64000
∵M 是 x 的一次函数,且 M 随 x增大而减小,∴当 x=8 时,M 最小,最少为 48640 元.
11. 某电脑经销商计划购进一批电脑机箱和液晶显示器,若购电脑机箱 10 台和液液晶显示
器 8 台,共需要资金 7000 元;若购进电脑机箱 2 台和液示器 5 台,共需要资金 4120 元.
(1)每台电脑机箱、液晶显示器的进价各是多少元?
(2)该经销商购进这两种商品共 50 台,而可用于购买这两种商品的资金不超过 22240 元.根
据市场行情,销售电脑机箱、液晶显示器一台分别可获利 10 元和 160 元.该经销商希望销
售完这两种商品,所获利润不少于 4100 元.试问:该经销商有哪几种进货方案?哪种方案
获利最大?最大利润是多少?
解:(1)设每台电脑机箱、液晶显示器的进价各是 x,y 元,
根据题意得:
10 8 7000
2 5 4120
x y
x y
,解得:
60
800
x
y
,
答:每台电脑机箱、液晶显示器的进价各是 60 元,800 元;
(2)设该经销商购进电脑机箱 m 台,购进液晶显示器(50-m)台,
根据题意得:
60 800(50 ) 22240
10 160(50 ) 4100
m m
m m
,解得:24≤m≤26,
因为 m要为整数,所以 m 可以取 24、25、26,从而得出有三种进货方式:
①电脑箱:24 台,液晶显示器:26 台,
②电脑箱:25 台,液晶显示器:25 台;
③电脑箱:26 台,液晶显示器:24 台.
∴方案一的利润:24×10+26×160=4400,
方案二的利润:25×10+25×160=4250,
方案三的利润:26×10+24×160=4100,
∴方案一的利润最大为 4400 元.
12.一工地计划租用甲、乙两辆车清理淤泥,从运输量来估算:若租两辆车合运,10 天可以
完成任务;若单独租用乙车完成任务则比单独租用甲车完成任务多用 15 天.
(1)甲、乙两车单独完成任务分别需要多少天?
(2)已知两车合运共需租金 65000 元,甲车每天的租金比乙车每天的租金多 1500 元.试
问:租甲乙车两车、单独租甲车、单独租乙车这三种方案中,哪一种租金最少?请说明理由.
解:(1)设甲车单独完成任务需要 x 天,乙单独完成需要 y 天,由题意可得:
15
11110
xy
yx
,
解得:
30
15
y
x
即甲车单独完成需要 15 天,乙车单独完成需要 30 天;
(2)设甲车租金为 a,乙车租金为 b,则根据两车合运共需租金 65000 元,甲车每天的租金
比乙车每天的租金多 1500 元可得:
1500
650001010
ba
ba
,解得:
2500
4000
b
a
.
①租甲乙两车需要费用为:65000 元;②单独租甲车的费用为:15×4000=60000 元;
③单独租乙车需要的费用为:30×2500=75000 元;
综上可得,单独租甲车租金最少.
13.为表彰在“缔造完美教室”活动中表现积极的同学,老师决定购买文具盒与钢笔作为奖
品.已知 5 个文具盒、2 支钢笔共需 100 元;4 个文具盒、7 支钢笔共需 161 元.
(1)每个文具盒、每支钢笔个多少元?
(2)时逢“五一”,商店举行“优惠促销”活动,具体办法如下:文具盒“九折”优惠;钢
笔 10 支以上超出部分“八折”优惠.若买 x个文具盒需要 1y 元,买 x 支钢笔需要 2y 元;求 1y 、
2y 关于 x的函数关系式;
(3)若购买同一种奖品,并且该奖品的数量超过 10 件,请你分析买哪种奖品省钱.
解:(1)设每个文具盒 x 元,每支钢笔 y 元,可列方程组得
16174
10025
yx
yx
, 解之得
15
14
y
x
答:每个文具盒 14 元,每支钢笔 15 元.
(2)由题意知,y1 关于 x 的函数关系式为 y1=14×90%x,即 y1=12.6x.
由题意知,买钢笔 10 以下(含 10 支)没有优惠,故此时的函数关系式为 y2=15x.
当买 10 支以上时,超出部分有优惠,故此时函数关系式为 y2=15×10+15×80%(x-10)
即 y2=12x+30
(3)当 y1< y2 即 12.6x<12x+30 时,解得 x<50;
当 y1= y2 即 12.6x=12x+30 时,解得 x=50;
当 y1> y2 即 12.6x>12x+30 时,解得 x>50.
综上所述,当购买奖品超过 10 件但少于 50 件时,买文具盒省钱;
当购买奖品超过 50 件时,买文具盒和买钢笔钱数相等;
当购买奖品超过 50 件时,买钢笔省钱.
14.为极大地满足人民生活的需求,丰富市场供应,我区农村温棚设施农业迅速发展,温棚
种植面积在不断扩大.在耕地上培成一行一行的矩形土埂,按顺序间隔种植不同农作物的方
法叫分垄间隔套种.科学研究表明:在塑料温棚中分垄间隔套种高、矮不同的蔬菜和水果(同
一种紧挨在一起种植不超过两垄),可增加它们的光合作用,提高单位面积的产量和经济效
益.
现有一个种植总面积为 540m 2
的矩形塑料温棚,分垄间隔套种草莓和西红柿共 24 垄,
种植的草莓或西红柿单种农作物的总垄数不低于 10 垄,又不超过 14 垄(垄数为正整数),它
们的占地面积、产量、利润分别如下:
占地面积(m 2 /垄) 产量(千克/垄) 利润(元/千克)
西红柿 30 160 1.1
草莓 15 50 1.6
(1)若设草莓共种植了 x垄,通过计算说明共有几种种植方案?分别是哪几种?
(2)在这几种种植方案中,哪种方案获得的利润最大?最大利润是多少?
解:(1)根据题意西红柿种了(24- x)垄
15 x +30(24- x )≤540 解得 x≥12
∵ x≤14,且 x是正整数 ∴ x =12,13,14
共有三种种植方案,分别是:
方案一:草莓种植 12 垄,西红柿种植 12 垄
方案二:草莓种植 13 垄,西红柿种植 11 垄
方案三:草莓种植 14 垄,西红柿种植 10 垄
(2)解法一:方案一获得的利润:12×50×1.6+12×160×1.1=3072(元)
方案二获得的利润:13×50×1.6+11×160×1.1=2976(元)
方案三获得的利润:14×50×1.6+10×160×1.1=2880(元)
由计算知,种植西红柿和草莓各 12 垄,获得的利润最大,
最大利润是 3072 元
解法二:若草莓种了 x垄,设种植草莓和西红柿共可获得利润 y元,则
422496)24(1601.1506.1 xxxy
∵ k -96<0 ∴ y随 x的增大而减小
又∵12≤ x ≤14,且 x是正整数
∴当 x =12 时, 最大y =3072(元)
专题三开放型问题
一、中考专题诠释
开放型问题是相对于有明确条件和明确结论的封闭型问题而言的,它是条件或结论给
定不完全、答案不唯一的一类问题.这类试卷已成为近年中考的热点,重在考查同学们分析、
探索能力以及思维的发散性,但难度适中.根据其特征大致可分为:条件开放型、结论开放
型、方法开放型和编制开放型等四类.
二、解题策略与解法精讲
解开放性的题目时,要先进行观察、实验、类比、归纳、猜测出结论或条件,然后严
格证明;同时,通常要结合以下数学思想方法:分类讨论,数形结合,分析综合,归纳猜想,
构建数学模型等。
三、中考考点精讲
考点一:条件开放型
条件开放题是指结论给定,条件未知或不全,需探求与结论相对应的条件.解这种开放问题
的一般思路是:由已知的结论反思题目应具备怎样的条件,即从题目的结论出发,逆向追
索,逐步探求.
例 1(2013•盐城)写出一个过点(0,3),且函数值 y随自变量 x的增大而减小的一次函数
关系式:.(填上一个答案即可)
思路分析:首先可以用待定系数法设此一次函数关系式是:y=kx+b(k≠0).根据已知条件
确定 k,b应满足的关系式,再根据条件进行分析即可.
解:设此一次函数关系式是:y=kx+b.
把 x=0,y=3代入得:b=3,
又根据 y随 x的增大而减小,知:k<0.
故此题只要给定 k一个负数,代入解出 b值即可.如 y=-x+3.(答案不唯一)
故答案是:y=-x+3.
点评:本题考查了一次函数的性质.掌握待定系数法,首先根据已知条件确定 k,b应满足
的关系式,再根据条件进行分析即可.
对应训练
1.(2013•达州)已知(x1,y1),(x2,y2)为反比例函数
ky
x
图象上的点,当 x1<x2
<0时,y1<y2,则 k的一个值可为 .(只需写出符合条件的一个 k的值)
1.-1
考点二:结论开放型:
给出问题的条件,让解题者根据条件探索相应的结论并且符合条件的结论往往呈现多样
性,这些问题都是结论开放问题.这类问题的解题思路是:充分利用已知条件或图形特征,
进行猜想、类比、联想、归纳,透彻分析出给定条件下可能存在的结论,然后经过论证作出
取舍.
例 2(2013•常德)请写一个图象在第二、四象限的反比例函数解读式:.
思路分析:根据反比例函数的性质可得 k<0,写一个 k<0的反比例函数即可.
解:∵图象在第二、四象限,
∴y=-
3
x
,
故答案为:y=-
3
x
.
点评:此题主要考查了反比例函数 y=
k
x
(k≠0),(1)k>0,反比例函数图象在一、三象限;
(2)k<0,反比例函数图象在第二、四象限内.
对应训练
2.(2013•山西)四川雅安发生地震后,某校九(1)班学生开展献爱心活动,积极向灾区
捐款.如图是该班同学捐款的条形统计图.写出一条你从图中所获得的信息: .(只要与统
计图中所提供的信息相符即可得分)
2.该班有 50 人参与了献爱心活动(答案不唯一)
考点三:条件和结论都开放的问题:
此类问题没有明确的条件和结论,并且符合条件的结论具有多样性,因此必须认真观察
与思考,将已知的信息集中分析,挖掘问题成立的条件或特定条件下的结论,多方面、多角
度、多层次探索条件和结论,并进行证明或判断.
例 3(2013•广东)如图,矩形 ABCD中,以对角线 BD为一边构造一个矩形 BDEF,使得
另一边 EF过原矩形的顶点 C.
(1)设 Rt△CBD的面积为 S1,Rt△BFC的面积为 S2,Rt△DCE的面积为 S3,则S1S2+S3
(用“>”、“=”、“<”填空);
(2)写出如图中的三对相似三角形,并选择其中一对进行证明.
思路分析:(1)根据 S1=
1
2
S 矩形BDEF,S2+S3=
1
2
S 矩形BDEF,即可得出答案.
(2)根据矩形的性质,结合图形可得:△BCD∽△CFB∽△DEC,选择一对进行证明即可.
解答:(1)解:∵S1=
1
2
BD×ED,S 矩形BDEF=BD×ED,
∴S1=
1
2
S 矩形BDEF,
∴S2+S3=
1
2
S 矩形BDEF,
∴S1=S2+S3.
(2)答:△BCD∽△CFB∽△DEC.
证明△BCD∽△DEC;
证明:∵∠EDC+∠BDC=90°,∠CBD+∠BDC=90°,
∴∠EDC=∠CBD,
又∵∠BCD=∠DEC=90°,
∴△BCD∽△DEC.
点评:本题考查了相似三角形的判定,注意掌握相似三角形的判定定理,最经常用的就是
两角法,此题难度一般.
对应训练
3.(2013•荆州)如图,△ABC 与△CDE 均是等腰直角三角形,∠ACB=∠DCE=90°,D
在 AB上,连结 BE.请找出一对全等三角形,并说明理由.
3.解:△ACD≌△BCE.
证明如下∵∠ACB=∠DCE=90°,
∴∠AC B-∠DCB=∠DCE-∠DCB,
即∠ACD=∠BCE.
∵△ABC 与△CDE 均是等腰直角三角形,∠ACB=∠DCE=90°,
∴CA=CB,CD=CE,
在△ACD 和△BCE 中,
CE CD
ACD BCE
CA CB
,∴△ACD≌△BCE.
四、中考真题演练
一、填空题
1.(2013•徐州)请写出一个是中心对称图形的几何图形的名称: .
1.平行四边形
2.(2013•钦州)请写出一个图形经过一、三象限的正比例函数的解读式.
2.y=x(答案不唯一).
3.(2013•连云港)若正比例函数 y=kx(k为常数,且 k≠0)的函数值 y随着 x的增大而减
小,则 k的值可以是 .(写出一个即可)
3.-2
4.(2013•连云港)若正比例函数 y=kx(k为常数,且 k≠0)的函数值 y随着 x的增大而减
小,则 k的值可以是 .(写出一个即可)
4.-2
5.(2013•北京)请写出一个开口向上,并且与 y 轴交于点(0,1)的抛物线的解读式,y=.
5.x2+1(答案不唯一)
6.(2013•莆田)如图,点 B、E、C、F在一条直线上,AB∥DE,BE=CF,请添加一个条
件,使△ABC≌△DEF.
6.AB=DE
7.(2013•绥化)如图,A,B,C三点在同一条直线上,∠A=∠C=90°,AB=CD,请添加
一个适当的条件,使得△EAB≌△BCD.
7.AE=CB
8.(2013•义乌市)如图,已知∠B=∠C,添加一个条件使△ABD≌△ACE(不标注新的字
母,不添加新的线段),你添加的条件是 .
8.AC=AB
9.(2013•齐齐哈尔)如图,要使△ABC与△DBA相似,则只需添加一个适当的条件是 (填
一个即可)
9.∠C=∠BAD
10.(2013•邵阳)如图所示,弦 AB、CD相交于点 O,连结 AD、BC,在不添加辅助线的
情况下,请在图中找出一对相等的角,它们是 .
10.∠A与∠C(答案不唯一)
11.(2013•吉林)如图,AB 是⊙O的弦,OC⊥AB 于点 C,连接 OA、OB.点 P 是半径
OB 上任意一点,连接 AP.若 OA=5cm,OC=3cm,则 AP 的长度可能是 cm(写出一个
符合条件的数值即可)
11.6
12.(2013•昭通)如图,AB是⊙O的直径,弦 BC=4cm,F是弦 BC的中点,∠ABC=60°.若
动点 E以 1cm/s的速度从 A点出发在 AB上沿着 A→B→A运动,设运动时间为 t(s)(0≤t
<16),连接 EF,当△BEF是直角三角形时,t(s)的值为.(填出一个正确的即可)
12.4s
三、解答题
13.(2013•杭州)(1)先求解下列两题:
①如图①,点 B,D在射线 AM上,点 C,E在射线 AN上,且 AB=BC=CD=DE,已知∠
EDM=84°,求∠A的度数;
②如图②,在直角坐标系中,点 A在 y轴正半轴上,AC∥x轴,点 B,C的横坐标都是 3,
且 BC=2,点 D在 AC上,且横坐标为 1,若反比例函数
ky
x
x 0的图象经过点 B,D,
求 k的值.
(2)解题后,你发现以上两小题有什么共同点?请简单地写出.
13.解:(1)①∵AB=BC=CD=DE,
∴∠A=∠BCA,∠CBD=∠BDC,∠ECD=∠CED,
根据三角形的外角性质,∠A+∠BCA=∠CBD,∠A+∠CDB=∠ECD,∠A+∠CED=∠EDM,
又∵∠EDM=84°,
∴∠A+3∠A=84°,
解得,∠A=21°;
②∵点 B在反比例函数 y=
k
x
图象上,点 B,C的横坐标都是 3,
∴点 B(3,
3
k
),
∵BC=2,
∴点 C(3,
3
k
+2),
∵AC∥x轴,点 D在 AC上,且横坐标为 1,
∴A(1,
3
k
+2),
∵点 A也在反比例函数图象上,
∴
3
k
+2=k,
解得,k=3;
(2)用已知的量通过关系去表达未知的量,使用转换的思维和方法.(开放题)
14.(2013•盐城)市交警支队对某校学生进行交通安全知识宣传,事先以无记名的方式随
机调查了该校部分学生闯红灯的情况,并绘制成如图所示的统计图.请根据图中的信息回答
下列问题:
(1)本次共调查了多少名学生?
(2)如果该校共有 1500 名学生,请你估计该校经常闯红灯的学生大约有多少人;
(3)针对图中反映的信息谈谈你的认识.(不超过 30个字)
14.解:(1)调查的总人数是:55+30+15=100(人);
(2)经常闯红灯的人数是:1500×
15
100
=225(人);
(3)学生的交通安全意识不强,还需要进行教育.