- 2021-11-10 发布 |
- 37.5 KB |
- 89页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
北师大版九年级数学[上册]期末检测数学试题和答案解析[精品4套]+上册数学导学案
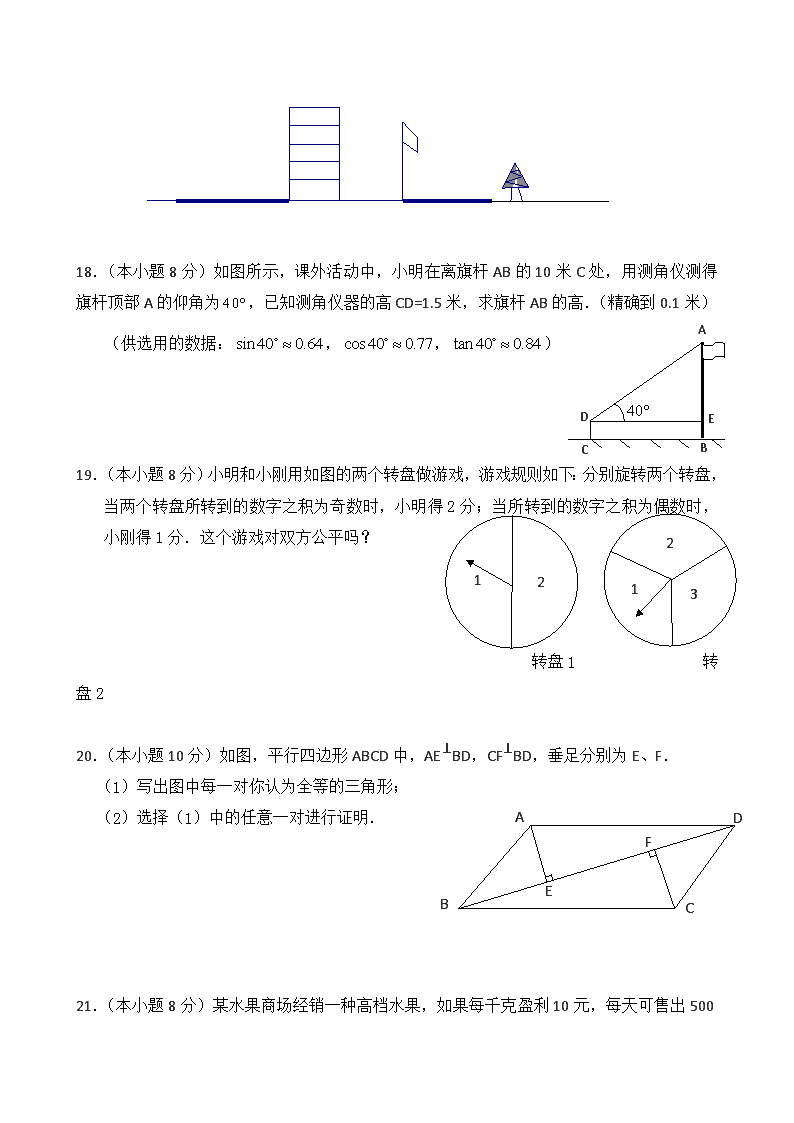
北师大版九年级数学[上册] 期末检测数学试题和答案解析[精品 4 套]+上册数学导学案 九年级数学上期末考试卷 一、选择题(本大题共 8 个小题,每题只有一个正确的选项,每小题 3分,满分 24 分) 1.一元二次方程 042 x 的解是( ) A. 2x B. 2x C. 21 x , 22 x D. 21 x , 22 x 2.二次三项式 2 4 3x x 配方的结果是( ) A. 2( 2) 7x B. 2( 2) 1x C. 2( 2) 7x D. 2( 2) 1x 3.小明从上面观察下图所示的两个物体,看到的是( ) A B C D 4.人离窗子越远,向外眺望时此人的盲区是( ) A.变小 B.变大 C.不变 D.以上都有可能 5.函数 x ky 的图象经过(1,-1),则函数 2 kxy 的图象是( ) 6.在 Rt△ABC 中,∠C=90°,a=4,b=3,则 sinA的值是( ) A. 5 4 B. 3 5 C. 4 3 D. 4 5 7.下列性质中正方形具有而矩形没有的是( ) A.对角线互相平分 B.对角线相等 正面 2 2 2 2 -2 -2 -2 -2O OOO y y y y xx x x A B C D C.对角线互相垂直 D.四个角都是直角 8.一只小狗在如图的方砖上走来走去,最终停在阴影方砖上的概率是( ) A. 15 4 B. 3 1 C. 5 1 D. 15 2 二、填空题(本大题共 7 个小题,每小题 3分,满分 21 分) 9.计算 tan60°= . 10.已知函数 2 2( 1) my m x 是反比例函数,则 m 的值为 . 11.若反比例函数 x ky 的图象经过点(3,-4),则此函数在每一个象限内 y 随 x的增大而 . 12.命题“直角三角形两条直角边的平方和等于斜边的平方”的逆命题是 . 13.有两组扑克牌各三张,牌面数字分别为 2,3,4,随意从每组中牌中抽取一张,数字和 是 6的概率是 . 14.依次连接矩形各边中点所得到的四边形是 . 15.如图,在△ABC 中,BC = 8 cm,AB 的垂直平分线交 AB 于点D,交边 AC于点 E,△BCE 的周长等于 18 cm, 则 AC的长等于 cm. 三、解答题(本大题共 9个小题,满分 75分) 16.(本小题 6 分)解方程: 3 ( 3)x x x 17.(本小题 6分)如图,楼房和旗杆在路灯下的影子如图所示。试确定路灯灯炮的位置,再 作出小树在路灯下的影子.(不写作法,保留作图痕迹) 得 分 评卷人 得 分 评卷人 A D B C E 18.(本小题 8 分)如图所示,课外活动中,小明在离旗杆 AB 的 10 米 C 处,用测角仪测得 旗杆顶部 A 的仰角为 40,已知测角仪器的高 CD=1.5 米,求旗杆 AB 的高.(精确到 0.1 米) (供选用的数据: sin 40 0.64 , cos 40 0.77 , tan 40 0.84 ) 19.(本小题 8 分)小明和小刚用如图的两个转盘做游戏,游戏规则如下:分别旋转两个转盘, 当两个转盘所转到的数字之积为奇数时,小明得 2 分;当所转到的数字之积为偶数时, 小刚得 1分.这个游戏对双方公平吗? 转盘 1 转 盘 2 20.(本小题 10分)如图,平行四边形 ABCD 中,AE⊥BD,CF⊥BD,垂足分别为 E、F. (1)写出图中每一对你认为全等的三角形; (2)选择(1)中的任意一对进行证明. 21.(本小题 8 分)某水果商场经销一种高档水果,如果每千克盈利 10 元,每天可售出 500 40 ED C B A 1 2 1 2 3 A B C D E F 千克,经市场调查发现,在进货价不变的情况下,出售价格每涨价 1元,日销售量将减少 20 千克,现该商场要保证每天盈利 6000元,同时又要使顾客得到实惠,那么每千克应涨价多少 元? 22.(本小题 10 分)已知:如图,D 是△ABC 中 BC 边上一点,E 是 AD 上的一点, EB=EC, ∠1=∠2. 求证:AD平分∠BAC. 23.(本小题 9 分)正比例函数 kxy 和反比例函数 x ky 的图象相交于 A,B 两点,已知点 A 的横坐标为 1,纵坐标为3. (1)写出这两个函数的表达式; (2)求 B 点的坐标; (3)在同一坐标系中,画出这两个函数的图象. 24.(本小题 10分)阅读探索:“任意给定一个矩形 A,是否存在另一个矩形 B,它的周长和 21 A B C D E O 1 2 3 4 5 6 6 5 4 3 2 1 -1-2-3-4-5-6 -1 -2 -3 -4 -5 -6 x y 面积分别是已知矩形周长和面积的一半?”(完成下列空格) (1)当已知矩形 A 的边长分别为 6 和 1 时,小亮同学是这样研究的: 设所求矩形的两边分别是 yx和 ,由题意得方程组: 3 2 7 xy yx , 消去 y 化简得: 0672 2 xx , ∵△=49-48>0,∴x1= ,x2= . ∴满足要求的矩形 B 存在. (2)如果已知矩形 A 的边长分别为 2 和 1,请你仿照小亮的方法研究是否存在满足要求的矩 形 B. (3)如果矩形 A 的边长为 m 和 n,请你研究满足什么条件时,矩形 B 存在? 九年级数学 参考答案 一、选择题 1.C 2.B 3.A 4.B 5.A 6.D 7.C 8.B 二、填空题 9. 3 10.-1 11.增大 12.如果三角形两边的平方和等于第三边的平方,那么这个三 角形是直角三角形 13. 1 3 14.菱形 15.10 三、解答题 16.(本小题 6分) 解方程得 x1=1,x2=3 17.(本小题 6分) 略 18.(本小题8分) 解:在 Rt△ADE 中, tan ADE= DE AE ∵ DE=10, ADE=40° ∴ AE=DE tan ADE =10 tan 40°≈10 0.84 =8.4 ∴ AB=AE+EB=AE+DC=8.4 1.5 9.9 答:旗杆 AB 的高为9.9米 19.解:∵P(奇数)= 3 1 P(偶数)= 3 2 ∵ 3 1 ×2= 3 2 ×1 ∴这个游戏对双方是公平的 20.解:(1)△ABD≌△CDB,△AEB≌△CFD,△AED≌△CFB(2)证明略 21.解:设每千克应涨价 x元,根据题意,得 (10 )(500 20 ) 6000x x 即 2 15 50 0x x , 解 得 x1=5,x2=10 ∵要使顾客得到实惠 ∴ 102 x 舍去 答:每千克应涨价 5 元。 22.(本小题 10分) 解:上面的证明过程不正确,错在第一步。 证明:∵EB=EC, ∴∠3=∠4 又∵∠1=∠2∴∠1+∠3=∠2+∠4 即∠ABC=∠ACB 转盘 2 转盘 1 1 2 3 1 1 2 3 2 2 4 6 21 A B CD E 3 4 ∴AB=AC∴在△AEB 和△AEC 中, EB=EC 1= 2 AB=AC ∴△AEB≌△AEC ∴∠BAE=∠CAE∴AD 平分∠BAC 23.解:(1)∵正比例函数 y=kx与反比例函数 x ky 的图像都过点 A(1,3),则 k=3∴正比例函数是 y=3x , 反比例函数是 3y x (2)∵点 A 与点 B 关于原点对称,∴点 B 的坐标是(-1,-3)(3)略 24.解:(1)2 和 3 2 ;(2) 3 2 1 x y xy ,消去 y 化简得:2 x2-3x+2=0,Δ=9-16<0,所以不存在矩形 B. (3)(m + n)2 -8mn≥0, 设所求矩形的两边分别是 yx和 ,由题意得方程组: 2 2 m nx y mnxy ,消去 y 化简得:2 x2-(m + n)x + mn = 0, Δ=(m + n)2 -8mn≥0. 即(m + n)2-8mn≥0 时,满足要求的矩形 B 存在 九年级数学上学期期末检测试题卷 一、选择题(本大题共 8 个小题,每题只有一个正确的选项,每小题 3分,满分 24 分) 1.下列方程中,是一元二次方程的是( ) A. 32 yx B. 2( 1) 3x C. 113 22 xxx D. 2 9x 2.有一实物如下左图,那么它的主视图是( ) 3.到三角形各顶点的距离相等的点是三角形( ) A.三条角平分线的交点 B.三条高的交点 C.三边的垂直平分线的交点 D.三条中线的交点 A B C D 4.甲、乙两地相距 60km,则汽车由甲地行驶到乙地所用时间 y(小时)与行驶速度 x(千米/时)之间的 函数图像大致是( ) 5.下列命题中,不正确的是( ) A.顺次连结菱形各边中点所得的四边形是矩形 B.有一个角是直角的菱形是正方形 C.对角线相等且垂直的四边形是正方形 D.有一个角是 60°的等腰三角形是等边三角形 6.在 Rt△ABC 中,∠C=90°,a=4,b=3,则 sinA 的值是( ) A. 4 5 B. 3 5 C. 4 3 D. 5 4 7.电影院呈阶梯或下坡形状的主要原因是( ) A.为了美观 B.减小盲区 C.增大盲区 D.盲区不变 8.某校九年级一班共有学生 50 人,现在对他们的生日(可以不同年)进行统计,则正确的说法是( ) A.至少有两名学生生日相同 B.不可能有两名学生生日相同 C.可能有两名学生生日相同,但可能性不大 D.可能有两名学生生日相同,且可能性很大 二、填空题(本大题共 7 个小题,每小题 3分,满分 21 分) 9.计算 2cos60°+ tan245°= 。 10.一元二次方程 2 3 0x x 的解是 。 11.请你写出一个反比例函数的解析式使它的图象在第一、三象限 。 12.在平行四边形 ABCD 中,对角线 AC 长为 10 cm,∠CAB=30°,AB= 6 cm,则平行四边形 ABCD 的面积 为 2cm 。 13.命题“等腰梯形的对角线相等”。它的逆命题是 . 14.随机掷一枚均匀的硬币两次,至少有一次正面朝上的概率是 。 15 . 已 知 反 比 例 函 数 ky x 的 图 像 经 过 点 ( 1 , - 2 ), 则 直 线 y = ( k - 1 ) x 的 解 析 式 为 。 三、解答题(本大题共 9 个小题,满分 75 分) 16.(本小题 6 分)解方程: 0672 xx O x y A O x y B O x y C O x D y 17.(本小题 6 分)为响应国家“退耕还林”的号召,改变我省水土流失严重的状况,2005 年我省退耕还 林 1600 亩,计划 2007 年退耕还林 1936 亩,问这两年平均每年退耕还林的增长率是多少? 18.(本小题 6 分)如图,小明为测量某铁塔 AB 的高度,他在离塔底 B 的 10 米 C 处测得塔顶的仰角α=43°, 已知小明的测角仪高 CD=1.5 米,求铁塔 AB 的高。(精确到 0.1 米) (参考数据:sin43° =0.6820, cos43° =0.7314, tan43° =0.9325) 19.(本小题 8 分)你吃过拉面吗?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉 面,面条的总长度 y(m)是面条的粗细(横截面积) s (mm2)的反比例函数,其图像如图所示。 (1)写出 y 与 s 的函数关系式; (2)求当面条粗 1.6mm2时,面条的总长度是多少米? 20.(本小题 8 分)两个布袋中分别装有除颜色外,其他都相同的 2 个白球,1 个黑球,同时从这两个布袋 中摸出一个球,请用列表法表示出可能出现的情况,并求出摸出的球颜色相同的概率。 21.(本小题 8 分)已知:四边形 ABCD 的对角线 AC、BD 相交于点 O,给出下列 5 个条件: ①AB∥DC;②OA=OC;③AB=DC;④∠BAD=∠DCB;⑤AD∥BC。 (1)从以上 5 个条件中任意选取 2 个条件,能推出四边形 ABCD 是平行四边形的有(用序号表示): 如①与⑤ 、 。(直接在横线上再写出两种) (2)对由以上 5 个条件中任意选取 2 个条件,不能推出四边形 ABCD 是平行四边形的,请选取一种情 形举出反例说明。 22.(本小题 9 分)在如图所示的三角形纸片 ABC 中,∠C=90°,∠B=30°,按如下步骤可以把这个直角 C A B ED α A B D O C 1 20 s(mm2) y(m) O 2 3 4 5 P(4,32) 60 40 80 100 A E 三角形纸片分成三个全等的小直角三角形(图中虚线表示折痕)。①先将点 B 对折到点 A,②将对折后 的纸片再沿 AD 对折。 (1)由步骤①可以得到哪些等量关系? (2)请证明△ACD≌△AED (3)按照这种方法能否将任意一个直角三角形分成三个全等的小三角形? 23.(本小题 12 分)如图,已知直线 y =-x+4 与反比例函数 y k x 的图象相交于点 A(-2,a),并且与 x 轴相交于点 B。 (1)求 a 的值; (2)求反比例函数的表达式; (3)求△AOB 的面积。 九年级数学(参考答案) 一、选择题 1.D 2.A 3.C 4.B 5.C 6.A 7.B 8.D 二、填空题 9.2 10.x1=0, x2=3 11. 2y x 12.30 13.对角线相等的梯形是等腰梯形 14. 1 4 15.y =-3x 三、解答题 16. 解方程得 x1=1,x2=6 17.解: 设平均增长率为 x ,则 1600(1+x)2=1936 解得:x1=0.1=10% x2=-2.1(舍去) 18.解:如图,可知四边形 DCBE 是矩形, 则EB = DC =1.5米,DE=CB=10米 在 Rt△AED中,∠ADE=α=43º C A B ED α x y A O B 那么tanα AE DE 所以,AE=DEtan43º =10×0.9325=9.325 所以,AB=AE+EB =9.325+1.5=10.825≈10.8(米) 19.(本小题 8分) 解:(1)设 y 与 s 的函数关系式为 s ky , 将 s=4,y=32代入上式,解得 k=4×32=128 所以 y 与 s 的函数关系式 s y 128 (2)当 s=1.6时, 80 6.1 128 y 所以当面条粗 1.6mm2时,面条的总长度是 80 米 20.(本小题 8分)列表得: 白球的概率= 4 9 黑球的概率= 1 9 21.(本小题 8分) 解:(1)①与②;①与③;①与④;②与⑤;④与⑤ (只要写出两组即可;每写一个给 2 分) (2)③与⑤ 反例:等腰梯形 22.(本小题 9分) 解:(1)AE=BE,AD=BD,∠B=∠DAE=30º, ∠BDE=∠ADE=60º,∠AED=∠BED=90º。 (2)在 Rt△ABC 中,∠B=30º,所以 AE=EB,因而 AC=AE 又因为∠CAD=∠EAD,AD=AD 所以△ACD≌△AED (3)不能 23.(本小题 12分) 解:(1)将 A(-2,a)代入 y=-x+4 中,得:a=-(-2)+4 所以 a =6 (2)由(1)得:A(-2,6) 将 A(-2,6)代入 x ky 中,得到 2 6 k 即 k=-12 所以反比例函数的表达式为: x y 12 (3)如图:过 A 点作 AD⊥x轴于 D; 因为 A(-2,6) 所以 AD=6 在直线 y=-x+4 中,令 y=0,得 x=4 所以 B(4,0) 即 OB=4 所以△AOB 的面积 S= 2 1 OB×AD= 2 1 ×4×6=12 24.(本小题 12分) , , ,, , , , , , ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 黑 黑 黑 ( ) 黑黑黑黑 黑 白 白白 白 白 白白白 白 白 白白 白 白 白白 袋2 袋1 x y A OD B A D B C 解:(1)菱形的一条对角线所在的直线。(或菱形的一组对边的中点所在的直线或菱形对角线 交点的任意一条直线)。 (2)三角形一边中线所在的直线。 (3)方法一:取上、下底的中点,过两点作直线得梯形的二分线(如图 1) 方法二:过 A、D作 AE⊥BC,DF⊥BC,垂足 E、F,连接 AF、DE 相交于 O,过点 O 任意 作直线即为梯形的二分线(如图 2) (如图 1) (如图 2) 九年级数学 一、选择题(每小题 3分,满分 24 分) 1.一元二次方程 2 5 6 0x x 的根是( ) A.x1=1,x2=6 B.x1=2,x2=3 C.x1=1,x2=-6 D.x1=-1,x2=6 2.下列四个几何体中,主视图、左视图与俯视图是全等图形的几何体是( ) A.球 B.圆柱 C.三棱柱 D.圆锥 A D B C E F O 3.到三角形三条边的距离相等的点是三角形( ) A.三条角平分线的交点 B.三条高的交点 C.三边的垂直平分线的交点 D.三条中线的交点 4.如果矩形的面积为 6cm2,那么它的长 y cm 与宽 x cm 之间的函数关系用图象表示 大致( ) A B C D 5.下列函数中,属于反比例函数的是( ) A. 3 xy B. 1 3 y x C. 5 2y x D. 2 1y x 6.在 Rt△ABC 中,∠C=90°,a=4,b=3,则 cosA 的值是( ) A. 4 5 B. 3 5 C. 4 3 D. 5 4 7.如图(1),△ABC 中,∠A=30°,∠C=90°AB 的垂直平分线 (1) 交 AC 于 D 点,交 AB 于 E 点,则下列结论错误的是( ) A、AD=DB B、DE=DC C、BC=AE D、AD=BC 8.顺次连结等腰梯形各边中点得到的四边形是 ( ) A、矩形 B、菱形 C、正方形 D、平行四边形 二、填空题(每小题 3分,满分 21 分) 9.计算 tan45°= . 10.已知函数 2 2( 1) my m x 是反比例函数,则 m的值为 . 11.请你写出一个反比例函数的解析式,使它的图象在第二、四象限 . 12.在直角三角形中,若两条直角边长分别为 6cm 和 8cm,则斜边上的中线长 为 cm. 13. 已知菱形的周长为 cm40 ,一条对角线长为 cm16 ,则这个菱形的面积 为 (cm) 2. 14.已知正比例函数 kxy 与反比例函数 0 k x ky 的一个交点是(2,3),则另 一个交点是( , ). 15.如图,已知 AC=DB,要使△ABC≌△DCB,需添加的一个 条件是 . 三、解答题(本大题共 9个小题,满分 75 分) 16.(本小题 8分)解方程: 2 ( 2)x x x A B C D y xO o y x y xo y xo 17.(本小题 8分)如图,在△ABD 中,C是 BD 上的一点, 且 AC⊥BD,AC=BC=CD.(1)求证:△ABD 是等腰三角形. (2)求∠BAD 的度数. 18.(本小题 8 分)如图所示,课外活动中,小明在离旗杆 AB 的10米 C处,用测角仪测得旗 杆顶部 A 的仰角为 40,已知测角仪器的高 CD=1.5米,求旗杆 AB 的高.(精确到0.1米) (供选用的数据: sin 40 0.64 , cos 40 0.77 , tan 40 0.84 ) 19.(本小题 8分)某商店四月份的营业额为 40 万元,五月份的营业额比四月份有所增长, 六月份比五月份又增加了 5个百分点,即增加了 5%,营业额达到了 50.6 万元。求五月份增 长的百分率。 20.(本小题 8 分)“一方有难,八方支援”.今年 11 月 2 日,鄂嘉出现洪涝灾害,牵动着全 县人民的心,医院准备从甲、乙、丙三位医生和 A、B 两名护士中选取一位医生和一名 护士支援鄂嘉防汛救灾工作. (1)若随机选一位医生和一名护士,用树状图(或列表法)表示所有可能出现的结果. (2)求恰好选中医生甲和护士 A的概率. 21.(本小题 8 分)如图,在△ABC 中,AC=BC,∠C=90°,AD 是△ABC 的角平分线,DE⊥AB, 垂足为 E. (1)已知 CD=4cm,求 AC 的长. (2)求证:AB=AC+CD. 40 ED C B A A C E D B 22.(8 分)在如图的 12×24 的方格形纸中(每个小方 格的边长都是 1 个单位)有一ΔABC. 现先把ΔABC 分别 向右、向上平移 8 个单位和 3 个单位得到ΔA1B1C1;再 以点 O 为旋转中心把ΔA1B1C1按顺时针方向旋转 90º得 到ΔA2B2C2. 请在所给的方格形纸中作出ΔA1B1C1和Δ A2B2C2. 23.(本题满分 9分) 如图,给出四个等式:①AE=AD;②AB=AC;③OB=OC;④∠B=∠C. 现选取其中的三个,以两 个作为已知条件,另一个作为结论. (1)请你写出一个正确的命题,并加以证明; (2)请你至少写出三个这样的正确命题. 24、(10 分)如图,已知反比例函数 x ky 2 和一次函数 y=2x-1,其中一次函数的图象经过(a,b), (a+1,b+k)两点. (1)求反比例函数的解析式; (2)如图4,已知点A在第一象限,且同时在上述两个函数的图象上,求点A的坐标; (3)利用(2)的结果,请问:在 x轴上是否存在点 P,使△AOP 为等腰三角形?若存在, 把符合条件的 P点坐标都求出来;若不存在,请说明理由. 九年级数学参考答案 一、选择题 1.D 2.A 3.A 4.C 5.B 6.B 7.B 8.B 二、填空题 9.1 10.1 11. 1y x …… 12.5 13.96 (cm)2 14.(-2,-3)15.AB=DC 或 ACB= DBC 三、解答题 16.(8 分) 解方程得 x1=1,x2=2 17.(8 分)解:(1)∵ AC⊥BD,AC=BC=CD ∴ C2 B2 A B C D E O ① ② ACB= ACD=90°∴ △ACB≌△ACD ∴ AB=AD ∴ △ABD 是等腰三角形.(2)∵ AC⊥BD,AC=BC=CD ∴ △ACB、△ACD 都是等腰直角三角形.∴ B= D=45° ∴ BAD=90° 18.解:在Rt△ADE中, tan ADE= DE AE ∵ DE=10, ADE=40° ∴ AE=DE tan ADE =10 tan 40°≈ 10 0.84 =8.4 ∴ AB=AE+EB=AE+DC=8.4 1.5 9.9 答:旗杆AB的高为9.9米 19.解:设五月份增长率为 x 40(1+x)(1+x+5%)=50.6 解得 x1=0.1,x2=-2.15(舍去) 20.( 8分)解:(1)用列表法或树状图表示所有可能结果如下: 列 表 法 : 树状图: (2)P(恰好选中医生甲和护士 A)= 1 6 , ∴恰好选中医生甲和护士 A 的概率是 1 6 21.(8 分) 解:(1)∵AD 是△ABC 的角平分线,DC⊥AC,DE⊥AB ∴DE=CD=4cm, 又∵AC=BC,∴∠B=∠BAC, 又∵∠C=90º,∴∠B=∠B DE=45º,∴BE=DE 在等腰直角三角形 BDE 中,由勾股定理得,BD=4 2 cm ∴AC=BC=CD+BD=4+4 2 (cm) (2)由(1)的求解过程可知:△ACD≌△AED,∴AC=AE, 又∵BE=DE=CD ∴AB=AE+BE=AC+CD 22.解:(8 分).ΔA1B1C1和ΔA2B2C2如图所示. 23.(9 分)(1)如果 AE=AD,AB=AC,那么∠B=∠C. 证明:在ΔABE 和ΔACD 中,∵AE=AD,∠A=∠A,AB=AC,∴ΔABE≌ΔACD,∴∠B=∠C. (2)①如果 AE=AD,AB=AC,那么 OB=OC. ②如果 AE=AD,∠B=∠C,那么 AB=AC. ③如果 OB=OC, ∠B=∠C,那么 AE=AD. 24.(10 分)解:(1)由题意得 1)1(2 12 akb ab ②-①得 2k ∴反比例函数的解析式为 x y 1 . (2)由 x y xy 1 12 解得 1 1 1 1 y x , 2 2 1 2 2 y x ∵点 A在第一象限,∴点 A 的坐标为(1,1) (3) 211 22 OA ,OA 与 x轴所夹锐角为 45°, ①当 OA 为腰时,由 OA=OP 得 P1( 2 ,0),P2(- 2 ,0);由 OA=AP 得 P3=(2,0). ②当 OA 为底时,得 P4=(1,0). ∴符合条件的点有 4 个,分别是( 2 ,0),(- 2 ,0),(2,0),(1,0) enjoy the trust of得到...的信任 have / put trust in信任 in trust受托的,代为保管的 take .一.选择题(本题有 10小题,每小题 2 分,共 20分) A B 甲 (甲, A) (甲, B) 乙 (乙, A) (乙, B) 丙 (丙, A) (丙, B) 护 士医 生 C 1.方程中,是关于 x的一元二次方程的是 ( )A. 1213 2 xx B. 0211 2 xx C. 02 cbxax D. 12 22 xxx 2.若反比例函数的图象经过(2,-2),(m,1),则 m= ( ) A.1 B.-1 C.4 D.-4 3.有一透明实物如图,那么它的主视图是 ( ) A B C D 4.如图,在等腰梯形 ABCD 中,AB∥CD,DC = 3 cm,∠A=60°,BD 平分∠ABC,则这个梯形的周长是( ) A. 21 cm B. 18 cm C. 15 cm D. 12 cm 5.三角形两边长分别为 3和 6,第三边是方程 2 6 8 0x x 的解,则这个三角形的周长是( )A.11 B.13 C.11 或 13 D.11 和 13 6.小明用两根同样长的竹棒做对角线,制作四边形的风筝,则该风筝的形状一定是( )A 矩形 B 正方形 C 等腰梯形 D 无法确定 7.既是轴对称,又是中心对称图形的是 ( ) A.矩形 B.平行四边形 C.正三角形 D.等腰梯形 8.中央电视台“幸运 52”栏目中的“百宝箱”互动环节,是一种竞猜游戏,游戏规则如下:在 20 个商标牌中,有 5 个商标牌的 背面注明一定的奖金额,其余商标的背面是一张哭脸,若翻到哭脸就不得奖金,参与这个游戏的观众有三次翻牌的机会(翻 过的牌不能再翻) .某观众前两次翻牌均获得若干奖金,那么他第三次翻牌获奖的概率是 ( )A. 4 1 B. 5 1 C. 6 1 D. 20 3 9.一元二次方程 2 5 6 0x x 的根是( ) A.x1=1,x2=6 B.x1=2,x2=3 C.x1=1,x2=-6 D.x1=-1,x2=6 10.下列四个几何体中,主视图、左视图与俯视图是全等图形的几何体是( ) A.球 B.圆柱 C.三棱柱 D.圆锥 11.到三角形三条边的距离相等的点是三角形( )A.三条角平分线的交点 B.三条高的交点 C.三边的垂直平分线的 交点 D.三条中线的交点 12.如果矩形的面积为 6cm 2 ,那么它的长 y cm 与宽 x cm 之间的函数关系用图象表示 大致( ) A B C D A B CD A B C y xO o y x y xo y xo y xo 13.下列函数中,属于反比例函数的是( ) A. 3 xy B. 1 3 y x C. 5 2y x D. 2 1y x 14.如图(1),△ABC 中,∠A=30°,∠C=90°AB 的垂直平分线交 AC于 D点,交 AB 于 E点,则下列结论错误的是( ) A、AD=DB B、DE=DC C、BC=AE D、AD=BC 15.顺次连结等腰梯形各边中点得到的四边形是 ( ) A、矩形 B、菱形 C、正方形 D、平行四边形 16.已知 3是关于 x的方程 3 4 x2-2a+1=0 的一个解,则 2a 的值是【 】 (A)11 (B)12 (C)13 (D)14 17.已知直角三角形的两边长是方程 x 2 -7x+12=0 的两根,则第三边长为【 】 (A)7 (B)5 (C) 7 (D)5 或 7 18.下列命题中错误的【 】 (A)两对邻角互补的四边形是平行四边形;(B)一组对边平行,一组对角相等的四边形是平行四边形 C等腰梯形的对角线 相等(D)平行四边形的对角线互相平分。 19.如图,在直角坐标系中,直线 y=6-x 与函数 y= x 4 (x>0)的图象 相交于点 A、B,设点 A的坐标为(x1,,y1),那么长为 x1,宽为 y1 的矩形的面积和周长分别为【 】 (A)4,12 (B)8,12 (C)4,6 (D)8,6 20.如图右,在双曲线上取一点 A向 x轴引 垂线,垂足为 B,连结 OA,若△AOB 的面积为 3 则双曲线的函数关系式为( ) A、 x y 3 B、 x y 3 C、 x y 6 D、 x y 6 21.一元二次方程 23 0x x 的解是( ) A. 0x B. 1 20 3x x , C. 1 2 10, 3 x x D. 1 3 x 22.下列各点,在反比例函数 x y 6 的图像上的是( ) A、(-2,-3) B、(1,6) C、(-3,2) D、(-6,-1) 23.某农场的粮食总产量为 1500 吨,设该农场人数为 x人,平均每人占有粮食数为 y 吨,则 y 与 x之间的函数图象大致 是( ) o A B x y 0 x y 0 y 0 A. B. 24. 已知关于 x的一元二次方程 0131 22 kxxk 有一根为 0,则 k=( ) A、1 B、-1 C、 1 D、 0 25. 2010 年某市政府投资 2亿元人民币建设了廉租房 8万平方米,预计到 2012 年底三年共累计投资 9.5 亿元人民币建设廉 租房,若在这两年内每年投资的增长率相同.设每年市政府投资的增长率为 x,根据题意,列出方程为( ) A 22 1+ ) 9 .5x ( B. 22 1+ ) 2(1 ) 9.5x x ( C 22+2 1 ) 2(1 ) 9.5x x ( D. 28 8 1+ ) 8(1 ) 9.5x x ( 26.若关于 x的方程 0962 xkx 有实数根,则 k 的取值范围是( ) A. 1k B. 1k C. 1 0k k 且 D. 1 0k k 且 27.已知方程 的一个根为 ,则另一个根是( ) A.5 B. C. D.3 28.如图,四边形 ABCD是矩形,F是 AD上一点,E是 CB延长线上一点,且四边形 AECF是等腰梯形,下列结论中,不一定 正确的是( ) A.AE=FC B.AD=BC C.BE=AF D.∠E=∠CFD 29.如图,在菱形 中,对角线 、 相交于点 O,E为 BC的中点,则下列式子中,一定成立的是( ) A. B. C. D. 30.在反比例函数 的图象的每一条曲线上, 都随 的增大而增大,则 的值可以是( )A.2 B.1 C.0 D. -1 31.用电器的输出功率 与通过的电流 、用电器的电阻 之间的关系是 ,下面说法中,正确的是( ) A. 为定值, 与 成反比例 B. 为定值, 与 成反比例 C. 为定值, 与 成正比例 D. 为定值, 与 成正比例 32.如图所示的两个转盘中,指针落在每一个数上的机会均等, 那么两个指针同时落在偶数上的概率是( ) A. 19 25 B. 10 25 C. 6 25 D. 5 25 33.下列命题中,不正确...的是( ) A.对角线相等的平行四边形是矩形. B.有一个角为 60°的等腰三角形是等边三角形.C.正方形的两条对角线相等且互相 A B C D E F 第 28 题图 D A B C EO 第 29 题图 垂直平分. D.直角三角形斜边上的高等于斜边的一半 34.某公司把 500 万元资金投入新产品的生产,第一年获得一定的利润,在不抽掉资金和利润的前提下,继续生产,第二 年的利润率比第一年提高 8%,若第二年的利润达到 112万元,设第一年的利润率为 x,则方程可以列为( ) A.500(1+x)(1+x+8%)=112 B.500(1+x)(1+x+8%)=112 +500 C.500(1+x)·8%=112 D.500(1+x)(x+8%)=112 35. 已知点(-2,y1),(-1,y2),(3,y3)都在反比例函数 x 6y 的图象上,那么 y1、y2 、y3的大小关系正确的是( ) A.y2查看更多