2019-2020学年河南郑州九年级上数学期中试卷

2019-2020学年河南郑州九年级上数学期中试卷

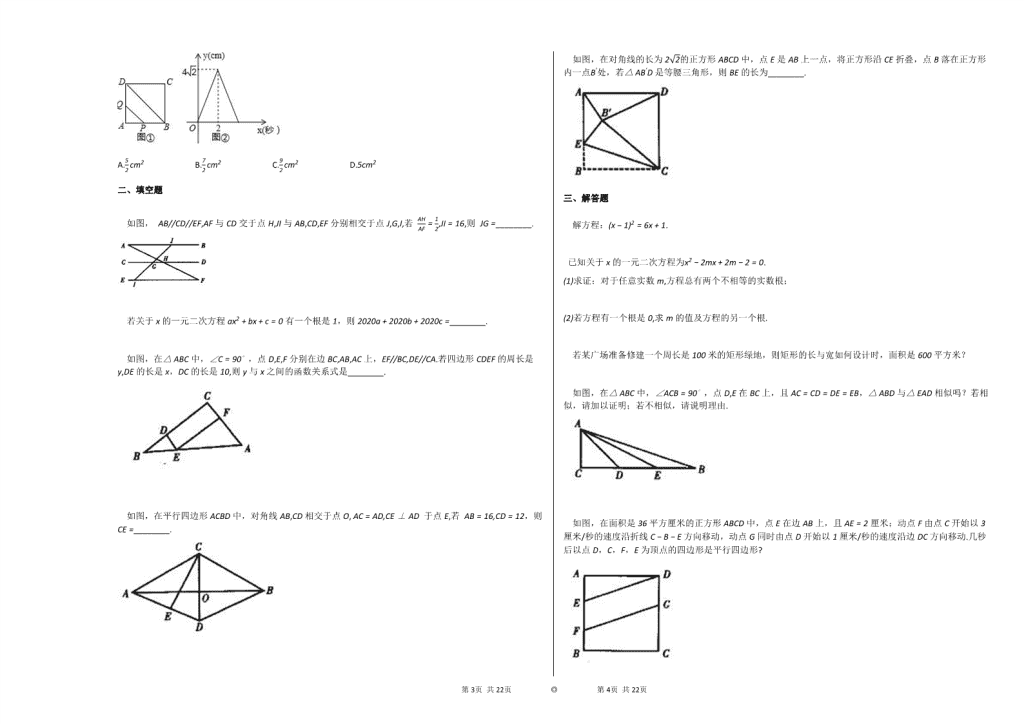
‎2019-2020学年河南郑州九年级上数学期中试卷 一、选择题 ‎ ‎ ‎1. 若‎2020a=2019b，则下列比例式不正确的是(        ) ‎ A.a:b=2019:2020‎ B.b:a=2020:2019‎ C.a:2020=b:2019‎ D.‎a:2019=b:2020‎ ‎ ‎ ‎2. 一元二次方程 x‎2‎‎=−x+1‎ 的二次项系数与常数项的和是‎(‎        ‎)‎ ‎ A.‎2‎ B.‎−2‎ C.‎1‎ D.‎‎0‎ ‎ ‎ ‎3. 一元二次方程 x(x+2020)−2019(x+2020)=0‎ 的两个根是（        ） ‎ A.x‎1‎‎=−2020,x‎2‎=2019‎ B.x‎1‎‎=2020,x‎2‎=−2019‎ C.x‎1‎‎=−2020,x‎2‎=−2019‎ D.x‎1‎‎=2020,x‎2‎=2019‎ ‎ ‎ ‎ ‎4. 若 x‎5‎‎=y‎6‎=‎z‎3‎ ，则x−yz−x 的值是（        ） ‎ A.‎−‎‎1‎‎2‎ B.‎−‎‎1‎‎3‎ C.‎1‎‎2‎ D.‎‎1‎‎3‎ ‎ ‎ ‎5. 若关于x的一元二次方程kx‎2‎+50x+25=0‎有两个不相等的实数根，则k的取值范围是‎(‎        ‎)‎ ‎ A.k<−25‎ B.k>25‎ C.k>−25‎且k≠0‎ D.k<25‎且k≠0‎ ‎ ‎ ‎6. 现有四张完全相同的卡片，上面分别标有数字‎0，−2，−1，1‎，把卡片背面朝上洗匀，然后从中随机抽取两张，则这两张卡片上的数字之和是负数的概率是(         ) ‎ A.‎1‎‎2‎ B.‎7‎‎12‎ C.‎2‎‎3‎ D.‎‎2‎‎5‎ ‎ ‎ ‎7. 如图，若在▱ ABCD 中，对角线AC，BD相交于点O，则下列判断正确的有(        ) ①若AC=BD,‎∠1=∠2‎，则▱ ABCD是正方形；②若‎∠2=∠3=‎‎45‎‎∘‎，则▱ ABCD是正方形；③若AC⊥BD,AC=BD，则▱ ABCD是正方形；④若AB=BC=CD=DA，则▱ ABCD是菱形；⑤若‎∠1=∠4‎，则▱ ABCD是菱形‎.‎ ‎ A.‎2‎个 B.‎3‎个 C.‎4‎个 D.‎5‎个 ‎ ‎ ‎8. 如图， ‎△ABC 是正三角形，点D、点E分别在BC,AC上，且 ‎∠ADE=‎‎60‎‎∘‎ ,则图中的相似三角形有(        ) ‎ A.‎1‎对 B.‎2‎对 C.‎3‎对 D.‎4‎对 ‎ ‎ ‎9. ‎ 如图，菱形ABCD的顶点A,B的坐标分别为 ‎(m,0),(n,0)‎ ,点D在y轴上，且‎|m−3|+(n+2‎)‎‎2‎=0‎.若点C的坐标是‎(x,y)‎，则‎(y−x‎)‎‎2‎=‎（        ） ‎ A.‎9‎ B.‎81‎ C.‎5‎ D.‎‎25‎ ‎ ‎ ‎10. 如图①，正方形ABCD的面积是‎16‎，点P以每秒‎2cm的速度从点A出发，沿AB→BC的路径运动，到点C停止．过点P作PQ // BD，PQ与边AD（或边CD）交于点Q，PQ的长y(cm)‎与点P的运动时间x（秒）的函数图象如图②所示．当点P运动‎2.5‎秒时，‎△CPQ的面积是(        ) ‎ A.‎5‎‎2‎cm‎2‎ B.‎7‎‎2‎cm‎2‎ C.‎9‎‎2‎cm‎2‎ D.‎‎5‎cm‎2‎ 二、填空题 ‎ ‎ 第21页 共22页 ◎ 第22页 共22页 ‎ 如图， AB//CD//EF,AF与CD交于点H,JI与AB,CD,EF分别相交于点J,G,I,若 AHAF‎=‎‎1‎‎2‎,JI=16‎,则 JG=‎________. ‎ ‎ ‎ ‎ 若关于x的一元二次方程ax‎2‎+bx+c=0‎有一个根是‎1‎，则‎2020a+‎‎2020b+2020c=‎________. ‎ ‎ ‎ ‎ 如图，在‎△ABC中，‎∠C=‎‎90‎‎∘‎，点D,E,F分别在边BC,AB,AC上，EF//BC,DE//CA.若四边形CDEF的周长是y,DE的长是x，DC的长是‎10‎,则y与x之间的函数关系式是________. ‎ ‎ ‎ ‎ 如图，在平行四边形ACBD中，对角线AB,CD相交于点O, AC=AD,CE⊥AD 于点E,若 AB=‎‎16‎‎,CD=12‎，则 CE=‎________. ‎ ‎ ‎ ‎ 如图，在对角线的长为‎2‎‎2‎的正方形ABCD中，点E是AB上一点，将正方形沿CE折叠，点B落在正方形内一点B‎′‎处，若‎△AB‎′‎D是等腰三角形，则BE的长为________. ‎ 三、解答题 ‎ ‎ ‎ 解方程：‎(x−1‎)‎‎2‎=6x+1‎. ‎ ‎ ‎ ‎ 已知关于x的一元二次方程为x‎2‎‎−2mx+2m−2=0‎. ‎ ‎(1)‎求证：对于任意实数m,方程总有两个不相等的实数根；‎ ‎ ‎ ‎(2)‎若方程有一个根是‎0‎,求m的值及方程的另一个根‎.‎ ‎ ‎ ‎ 若某广场准备修建一个周长是‎100‎米的矩形绿地，则矩形的长与宽如何设计时，面积是‎600‎平方米？ ‎ ‎ ‎ ‎ 如图，在‎△ABC中，‎∠ACB=‎‎90‎‎∘‎，点D,E在BC上，且AC=CD=DE=EB，‎△ABD与‎△EAD相似吗？若相似，请加以证明；若不相似，请说明理由. ‎ ‎ ‎ ‎ 如图，在面积是‎36‎平方厘米的正方形ABCD中，点E在边AB上，且AE=2‎厘米；动点F由点C开始以‎3‎厘米/秒的速度沿折线C−B−E方向移动，动点G同时由点D开始以‎1‎厘米/秒的速度沿边DC方向移动.几秒后以点D，C，F，E为顶点的四边形是平行四边形? ‎ ‎ ‎ 第21页 共22页 ◎ 第22页 共22页 ‎ 欢欢与乐乐做游戏，设置了如下游戏器材‎.‎如图是一个可以自由转动的转盘，被分成‎4‎个相等的扇形，分别标有数字‎4,3,2,1‎；另有一个不透明的口袋，装有分别标有数字‎1,3,5‎的三个小球（除数字不同外，其余都相同），欢欢转动一次转盘，停止后指针指向某一扇形，扇形内的数是欢欢的幸运数，乐乐任意摸出一个小球，小球上的数是乐乐的吉祥数，然后计算这两个数的积‎.‎ ‎ ‎(1)‎请你用画树状图或列表的方法，求这两个数的积为‎3‎的倍数的概率；‎ ‎ ‎ ‎(2)‎欢欢与乐乐做游戏，规则是：若这两个数的积为质数，则欢欢赢；若这两个数的积为合数，则乐乐赢；你认为该游戏公平吗？并说明理由‎.‎ ‎ ‎ ‎ ‎ a,b,c是‎△ABC的三边长，根据已知条件解答下列问题： ‎ ‎(1)‎若‎△ABC是等边三角形，解方程ax‎2‎+bx−c=0‎；‎ ‎ ‎ ‎(2)‎若关于x的方程‎(c+b)x‎2‎−2ax+c−b=0‎ 有两个相等的实数根，试判断‎△ABC的形状，并说明理由；‎ ‎ ‎ ‎(3)‎若a‎2‎‎+b‎2‎+c‎2‎=ab+ac+bc,试判断‎△ABC的形状，并说明理由‎.‎ ‎ ‎ ‎ ‎ ‎(1)‎探究证明：如图①所示，矩形ABCD的对角线相交于点O,点E是AB上一点，EG⊥OA于点G,EF⊥OB于点F, BH⊥OA 于点H,请你利用面积之间的关系探究证明EG+EF=BH；‎ ‎ ‎ ‎(2)‎发现探究：若‎(1)‎中的其他条件不变，当点E在AB的延长线时，如图②所示，请你猜想‎(1)‎中的结论是否成立，并说明理由；‎ ‎ ‎ ‎(3)‎拓展迁移：如图③所示，菱形ABCD的对角线相交于点O,点E是‎△ABC内一点，EG⊥‎AB于点G, EF⊥BC于点F,EH⊥OA于点H，若‎∠ABC=‎‎60‎‎∘‎，则请你直接写出EG,EF,EH,BO之间的等量关系：__________. ‎ 第21页 共22页 ◎ 第22页 共22页 参考答案与试题解析 ‎2019-2020学年河南郑州九年级上数学期中试卷 一、选择题 ‎1.‎ ‎【答案】‎ C ‎【考点】‎ 比例的性质 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 解：由‎2020a=2019b，可得‎2020‎‎2019‎‎=‎ba，或‎2020‎b‎=‎‎2019‎a， 即‎2020:2019=b:a或‎2020:b=2019:a， 即a:b=2019:2020‎或a:2019=b:2020‎， 分子分母互换可得‎2019:2020=a:b， 故A，B，D正确，C错误. 故选C.‎ ‎2.‎ ‎【答案】‎ D ‎【考点】‎ 一元二次方程的一般形式 一元二次方程的定义 ‎【解析】‎ 将其化为一般式为x‎2‎‎+x−1=0‎，二次项系数为‎1‎，常数项为‎−1‎，所以其和为‎1−1=0‎ 故选D ‎【解答】‎ 解：将其化为一般式为x‎2‎‎+x−1=0‎， 二次项系数为‎1‎，常数项为‎−1‎， 所以其和为‎1−1=0‎. 故选D. ‎ ‎3.‎ ‎【答案】‎ A ‎【考点】‎ 解一元二次方程-因式分解法 ‎【解析】‎ ‎1‎ ‎【解答】‎ 解：由x(x+2020)−2019(x+2020)=0‎得： ‎(x−2019)(x+2020)=0‎， 解得：x‎1‎‎=−2020‎，x‎2‎‎=2019‎. 故选A. ‎ ‎4.‎ ‎【答案】‎ C ‎【考点】‎ 比例的性质 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 解：设x‎5‎‎=y‎6‎=‎z‎3‎‎=k， 则x=5k，y=6k，z=3k， 则x−yz−x‎=‎‎5k−6k‎3k−5k‎=‎‎−k‎−2k‎=‎‎1‎‎2‎. 故选C. ‎ ‎5.‎ ‎【答案】‎ D ‎【考点】‎ 根的判别式 一元二次方程的定义 ‎【解析】‎ 先根据方程有两个不相等的实数根得出关于k的不等式组，求出k的取值范围即可．‎ ‎【解答】‎ 解：∵ 一元二次方程kx‎2‎+50x+25=0‎有两个不相等的实数根， ∴ Δ>0，‎k≠0，‎即Δ=2500−100k>0，‎k≠0，‎ 解得k<25‎且k≠0‎． 故k的取值范围是k<25‎且k≠0‎． 故选D．‎ ‎6.‎ ‎【答案】‎ C ‎【考点】‎ 概率公式 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 解：抽取的结果有‎(0,−2)‎，‎(0,−1)‎，‎(0,1)‎，‎(−2,−1)‎，‎(−2,1)‎，‎(−1,1)‎，共‎6‎种， 则这两张卡片上的数字之和是负数的有‎(0,−2)‎，‎(0,−1)‎，‎(−2,−1)‎，‎(−2,1)‎，共‎4‎种， 则这两张卡片上的数字之和是负数的概率是P=‎4‎‎6‎=‎‎2‎‎3‎. 故选C.‎ 第21页 共22页 ◎ 第22页 共22页 ‎7.‎ ‎【答案】‎ D ‎【考点】‎ 正方形的判定 菱形的判定 平行四边形的性质 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 解：因为四边形ABCD为平行四边形，所以AD=BC，AB=CD，‎∠1+∠4=∠2+∠3‎， ①若‎∠1=∠2‎，则AD=AB，‎∠3=∠4‎，同理BC=CD，所以AB=BC=CD=AD，所以平行四边形ABCD为菱形， 因为AC=BD，所以菱形ABCD为正方形，故①正确； ②若‎∠2=∠3=‎‎45‎‎∘‎，则‎∠D=‎‎90‎‎∘‎， 又因为‎∠1+∠4=∠2+∠3‎，所以‎∠1=∠4=∠2=∠3‎，所以四边形ABCD为菱形， 又因为‎∠ADC=‎‎90‎‎∘‎，所以菱形ABCD为正方形，故②正确； ③若AC⊥BD，AC=BD，则平行四边形ABCD是正方形，故③正确； ④若AB=BC=CD=DA，则平行四边形ABCD是菱形，故④正确； ⑤若‎∠1=∠4‎，因为‎∠4=∠2‎，所以‎∠1=∠2‎， 则AD=AB，‎∠3=∠4‎，同理BC=CD， 所以AB=BC=CD=AD，则平行四边形ABCD是菱形，故⑤正确. 综上，正确的有‎5‎个. 故选D.‎ ‎8.‎ ‎【答案】‎ B ‎【考点】‎ 相似三角形的判定 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 解：∵ 三角形ABC是正三角形， ∴ ‎∠B=∠C=∠BAC=‎‎60‎‎∘‎， ∴ ‎∠ADC=∠ADE+∠CDE=∠B+∠BAD， ∵ ‎∠ADE=∠B=‎‎60‎‎∘‎， ∴ ‎∠CDE=∠BAD， 在‎△ABD和‎△DCE中， ‎∠B=∠C，‎‎∠CDE=∠BAD，‎ ∴ ‎△ABD∼△DCE； 在‎△CAD和‎△DAE中， ‎∠C=∠ADE，‎‎∠CAD=∠DAE，‎ ∴ ‎△CAD∼△DAE， 即图中共有‎2‎对三角形相似. 故选B.‎ ‎9.‎ ‎【答案】‎ B ‎【考点】‎ 菱形的性质 坐标与图形性质 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 解：由题得：m−3=0‎,n+2=0‎, 所以OA=m=3‎，OB=n=‎−2‎=2‎， 所以AD=AB=5‎, 由勾股定理可得OD=AD‎2‎‎−‎OA‎2‎=4‎, 所以y=4‎，x=−CD=−5‎, 所以‎(y−x)‎‎2‎‎=‎(4+5)‎‎2‎=81‎. 故选B.‎ ‎ ‎10.‎ ‎【答案】‎ C ‎【考点】‎ 动点问题 ‎【解析】‎ 根据运动速度乘以时间，可得PQ的长，根据线段的和差，可得CP的长，根据勾股定理，可得答案．‎ ‎【解答】‎ 解：由面积为‎16‎可知，正方形边长为‎16‎‎=4‎ 点P运动‎2.5‎秒时，P点运动了‎5cm， CP=8−5=3cm， 因为PQ//BD，显然CQ=3cm， 则S‎△CPQ‎=‎1‎‎2‎×3×3=‎9‎‎2‎cm‎2‎. 故选C. ‎ 二、填空题 ‎【答案】‎ ‎8‎ ‎【考点】‎ 平行线分线段成比例 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 解：∵ AB//CD//EF，AHAF‎=‎‎1‎‎2‎， ∴ JGJI‎=‎‎1‎‎2‎， ∵ ‎ 第21页 共22页 ◎ 第22页 共22页 JI=16‎‎， ∴ JG=8‎. 故答案为：‎8‎.‎ ‎【答案】‎ ‎0‎ ‎【考点】‎ 列代数式求值 一元二次方程的解 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 解：ax‎2‎+bx+c=0‎有一个根是‎1‎， 将‎1‎代入得a+b+c=0‎， 则‎2020a+‎‎2020b+2020c=‎‎2020(a+b+c)=0‎. 故答案为：‎0‎.‎ ‎【答案】‎ y=2x+20‎ ‎【考点】‎ 平行四边形的性质与判定 由实际问题抽象出一元一次方程 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 解：由EF//BC,DE//CA可知： 四边形CDEF为平行四边形， ∴ CD=EF=10‎,CF=DE=x， ∴ y=CD+EF+CF+DE=2x+20‎. 故答案为：y=2x+20‎. ‎ ‎【答案】‎ ‎9.6‎ ‎【考点】‎ 相似三角形的性质与判定 菱形的性质 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 解：∵ 四边形ACBD是平行四边形，且AC=AD， ∴ 四边形ACBD是菱形， ∴ AB⊥CD， ∵ AB=16‎，CD=12‎， ∴ AD=OA‎2‎+OD‎2‎=‎8‎‎2‎‎+‎‎6‎‎2‎=10‎， 在‎△AOD和‎△CED中， ‎∠CDE=∠ADO，‎‎∠CED=∠AOD，‎ ∴ ‎△AOD∼△CED, ∴ CDAD‎=‎CEAO， 即‎12‎‎10‎‎=‎CE‎8‎， ∴ CE=9.6‎. 故答案为：‎9.6‎.‎ ‎【答案】‎ ‎4−2‎‎3‎或‎2‎‎3‎‎3‎ ‎【考点】‎ 正方形的性质 翻折变换（折叠问题）‎ 等腰三角形的性质 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 解：∵ 四边形ABCD是正方形，对角线为‎2‎‎2‎，‎ ‎∴ AB=BC=CD=AD=2‎，‎ ‎①当AD=B‎′‎D时，如图‎1‎， ‎ 由翻折的性质得，B‎′‎C=BC，‎ ‎∴ B‎′‎D=B‎′‎C=CD，‎ ‎∴ ‎△CDB‎′‎是等边三角形，‎ ‎∴ ‎∠B‎′‎DC=‎‎60‎‎∘‎，‎ ‎∴ ‎∠ADB‎′‎=‎‎30‎‎∘‎，‎ 过B‎′‎作B‎′‎G⊥AD于G，B‎′‎F⊥AB于F,‎ ‎∴ AF=B‎′‎G=‎1‎‎2‎×2=1‎，DG=‎‎3‎，‎ ‎∴ AG=FB‎′‎=2−‎‎3‎，‎ ‎∵ BE=B‎′‎E，EF=1−BE，‎ ‎∴ ‎(2−‎3‎‎)‎‎2‎+(1−BE‎)‎‎2‎=BE‎2‎，‎ 第21页 共22页 ◎ 第22页 共22页 ‎∴ BE=4−2‎‎3‎；‎ ‎②当 AB‎′‎=B‎′‎D时，如图‎2‎， ‎ 则B‎′‎在AD的垂直平分线上，‎ ‎∴ B‎′‎在BC的垂直平分线上，‎ ‎∴ BB‎′‎=CB‎′‎，‎ 由翻折的性质得，B‎′‎C=BC，‎ ‎∴ ‎△BB‎′‎C是等边三角形，‎ ‎∴ ‎∠BCE=‎‎30‎‎∘‎， ∴ BE=‎1‎‎2‎CE， ∴ BE‎2‎+BC‎2‎=CE‎2‎， 则‎2‎‎2‎‎+BE‎2‎=(2BE‎)‎‎2‎， ∴ BE=‎‎2‎‎3‎‎3‎. 故答案为：‎4−2‎‎3‎或‎2‎‎3‎‎3‎.‎ 三、解答题 ‎【答案】‎ 解：原方程变形为 x‎2‎‎−8x=0‎. 方程的左边分解因式，得 x(x−8)=0‎. 所以x=0‎或x−8=0‎. 所以x‎1‎‎=0,x‎2‎=8‎.‎ ‎【考点】‎ 解一元二次方程-因式分解法 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 解：原方程变形为 x‎2‎‎−8x=0‎. 方程的左边分解因式，得 x(x−8)=0‎. 所以x=0‎或x−8=0‎. 所以x‎1‎‎=0,x‎2‎=8‎.‎ ‎【答案】‎ ‎(1)‎证明：Δ=(−2m‎)‎‎2‎−4(2m−2)=4m‎2‎−8m+8‎ ‎=4(m‎2‎−2m+2)=4(m−1‎)‎‎2‎+4‎. ∵ 无论m为何值，‎(m−1‎)‎‎2‎≥0,‎ ‎∴4(m−1‎)‎‎2‎+4>0,‎ ∴ 对于任意实数m,方程总有两个不相等的实数根‎.‎ ‎(2)‎解：∵ 方程的一个根是‎0‎， 将‎0‎代入方程，得： ‎∴2m−2=0‎,∴ m=1‎． ∴ 原方程为x‎2‎‎−2x=0‎ , 解得x‎1‎‎=0,x‎2‎=2.‎ ‎∴m的值为‎1‎,方程的另一个根是‎2.‎ ‎【考点】‎ 根的判别式 一元二次方程的解 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ ‎(1)‎证明：Δ=(−2m‎)‎‎2‎−4(2m−2)=4m‎2‎−8m+8‎ ‎=4(m‎2‎−2m+2)=4(m−1‎)‎‎2‎+4‎. ∵ 无论m为何值，‎(m−1‎)‎‎2‎≥0,‎ ‎∴4(m−1‎)‎‎2‎+4>0,‎ ∴ 对于任意实数m,方程总有两个不相等的实数根‎.‎ ‎(2)‎解：∵ 方程的一个根是‎0‎， 将‎0‎代入方程，得： ‎∴2m−2=0‎,∴ m=1‎．  ∴ 原方程为x‎2‎‎−2x=0‎ , 解得x‎1‎‎=0,x‎2‎=2.‎ ‎∴m的值为‎1‎,方程的另一个根是‎2.‎ ‎【答案】‎ 解：设矩形的长是x米，则矩形的宽是‎100−2x‎2‎‎=(50−x)‎米. 根据题意，得x(50−x)=600‎. 解得x‎1‎‎=20,x‎2‎=30‎. 因为长大于宽，所以x=30‎. 所以宽为：‎50−x=50−30=20‎. 答：矩形的长与宽分别是‎30‎米与‎20‎米时，面积是‎600‎平方米.‎ ‎【考点】‎ 一元二次方程的应用--几何图形面积问题 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 第21页 共22页 ◎ 第22页 共22页 解：设矩形的长是x米，则矩形的宽是‎100−2x‎2‎‎=(50−x)‎米. 根据题意，得x(50−x)=600‎. 解得x‎1‎‎=20,x‎2‎=30‎. 因为长大于宽，所以x=30‎. 所以宽为：‎50−x=50−30=20‎. 答：矩形的长与宽分别是‎30‎米与‎20‎米时，面积是‎600‎平方米.‎ ‎【答案】‎ 解：‎△ABD∼△EAD. 理由如下： ‎∵AC=CD=DE=EB,‎ ‎∴‎可设AC=CD=DE=EB=1,‎ ‎∴CE=2,BD=2,CB=3.‎ ‎∵∠ACB=‎90‎‎∘‎,‎ ‎∴AD=‎1‎‎2‎‎+‎‎1‎‎2‎=‎2‎,AE=‎1‎‎2‎‎+‎‎2‎‎2‎=‎5‎,AB=‎1‎‎2‎‎+‎‎3‎‎2‎=‎10‎,‎ ‎∴ABEA=‎10‎‎5‎=‎2‎,BDAD=‎2‎‎2‎=‎2‎,ADED=‎2‎‎1‎=‎2‎,‎ ‎∴ABEA=BDAD=ADED,‎ ∴ ‎△ABD∼△EAD. ‎ ‎【考点】‎ 相似三角形的性质与判定 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 解：‎△ABD∼△EAD. 理由如下： ‎∵AC=CD=DE=EB,‎ ‎∴‎可设AC=CD=DE=EB=1,‎ ‎∴CE=2,BD=2,CB=3.‎ ‎∵∠ACB=‎90‎‎∘‎,‎ ‎∴AD=‎1‎‎2‎‎+‎‎1‎‎2‎=‎2‎,AE=‎1‎‎2‎‎+‎‎2‎‎2‎=‎5‎,AB=‎1‎‎2‎‎+‎‎3‎‎2‎=‎10‎,‎ ‎∴ABEA=‎10‎‎5‎=‎2‎,BDAD=‎2‎‎2‎=‎2‎,ADED=‎2‎‎1‎=‎2‎,‎ ‎∴ABEA=BDAD=ADED,‎ ∴ ‎△ABD∼△EAD. ‎ ‎【答案】‎ 解：设ts后以点D，G，F，E为顶点的四边形是平行四边形，此时点F一定在AB上， ∵ 正方形ABCD的面积是‎36‎平方厘米， ‎∴AB=BC=6‎厘米，EF//DG,‎ ‎∴FB=3t−6‎，EF=6−2−(3t−6)=10−3t，DG=t. ‎∵EF//DG,‎ ∴ 当EF=DG时，四边形DGFE是平行四边形， ‎∴10−3t=t,‎ ‎∴t=‎5‎‎2‎,‎ 即当t=‎‎5‎‎2‎秒时，以点D，G，F，E为顶点的四边形是平行四边形‎.‎ ‎ ‎【考点】‎ 动点问题 正方形的性质 平行四边形的判定 由实际问题抽象出一元一次方程 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 解：设ts后以点D，G，F，E为顶点的四边形是平行四边形，此时点F一定在AB上， ∵ 正方形ABCD的面积是‎36‎平方厘米， ‎∴AB=BC=6‎厘米，EF//DG,‎ ‎∴FB=3t−6‎，EF=6−2−(3t−6)=10−3t，DG=t. ‎∵EF//DG,‎ ∴ 当EF=DG时，四边形DGFE是平行四边形， ‎∴10−3t=t,‎ ‎∴t=‎5‎‎2‎,‎ 即当t=‎‎5‎‎2‎秒时，以点D，G，F，E为顶点的四边形是平行四边形‎.‎ ‎【答案】‎ 解：‎(1)‎列表如下： 由表格可以看出，所有机会均等的结果有‎12‎种，其中积为‎3‎的倍数的有‎6‎种， 所以这两个数的积为‎3‎的倍数的概率为‎6‎‎12‎‎=‎‎1‎‎2‎.‎ ‎(2)‎该游戏不公平‎.‎ 理由如下： 这两个数的积为质数的有：‎2‎，‎3‎，‎3‎，‎5‎，共‎4‎种， 这两个数的积为合数的有：‎4‎，‎6‎，‎9‎，‎10‎，‎12‎，‎15‎，‎20‎，共‎7‎种， 这两个数的积为质数的概率为‎4‎‎12‎‎=‎‎1‎‎3‎ ，积为合数的概率为‎7‎‎12‎‎,‎ 且‎1‎‎3‎‎<‎‎7‎‎12‎所以该游戏不公平‎.‎ ‎【考点】‎ 第21页 共22页 ◎ 第22页 共22页 游戏公平性 列表法与树状图法 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 解：‎(1)‎列表如下： 由表格可以看出，所有机会均等的结果有‎12‎种，其中积为‎3‎的倍数的有‎6‎种， 所以这两个数的积为‎3‎的倍数的概率为‎6‎‎12‎‎=‎‎1‎‎2‎.‎ ‎(2)‎该游戏不公平‎.‎ 理由如下： 这两个数的积为质数的有：‎2‎，‎3‎，‎3‎，‎5‎，共‎4‎种， 这两个数的积为合数的有：‎4‎，‎6‎，‎9‎，‎10‎，‎12‎，‎15‎，‎20‎，共‎7‎种， 这两个数的积为质数的概率为‎4‎‎12‎‎=‎‎1‎‎3‎ ，积为合数的概率为‎7‎‎12‎‎,‎ 且‎1‎‎3‎‎<‎‎7‎‎12‎所以该游戏不公平‎.‎ ‎【答案】‎ 解：‎(1)‎∵ ‎△ABC 是等边三角形， ‎∴a=b=c.‎ ‎∵ax‎2‎+bx−c=0,‎ ‎∴x‎2‎+x−1=0,‎ 解得x‎1‎‎=‎−1+‎‎5‎‎2‎,x‎2‎=‎‎−1−‎‎5‎‎2‎.‎ ‎(2)‎‎△ABC‎ 是直角三角形‎.‎ 理由如下： ∵ 方程‎(c+b)x‎2‎−2ax+c−b=0‎有两个相等的实数根， ‎∴(−2a‎)‎‎2‎−4(c+b)(c−b)=4a‎2‎−4c‎2‎+4b‎2‎=0‎， ‎∴a‎2‎−c‎2‎+b‎2‎=0‎， ‎∴a‎2‎+b‎2‎=‎c‎2‎， ∴ ‎△ABC 是直角三角形‎.‎ ‎(3)‎‎△ABC‎ 是等边三角形‎.‎ 理由如下： ‎∵a‎2‎+b‎2‎+c‎2‎=ab+ac+bc， ‎∴2a‎2‎+2b‎2‎+2c‎2‎=2ab+2ac+2bc.‎ ‎∴(a‎2‎−2ab+b‎2‎)+(b‎2‎−2bc+c‎2‎)+(a‎2‎−2ac+c‎2‎)=0‎， ‎∴(a−b‎)‎‎2‎+(b−c‎)‎‎2‎+(a−c‎)‎‎2‎=0‎， ‎∴a−b=0,b−c=0,a−c=0‎， ‎∴a=b,b=c,a=c， ‎∴a=b=c， ‎∴ △ABC是等边三角形.‎ ‎【考点】‎ 根的判别式 解一元二次方程-公式法 勾股定理的逆定理 等边三角形的判定 等边三角形的性质 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 解：‎(1)‎∵ ‎△ABC 是等边三角形， ‎∴a=b=c.‎ ‎∵ax‎2‎+bx−c=0,‎ ‎∴x‎2‎+x−1=0,‎ 解得x‎1‎‎=‎−1+‎‎5‎‎2‎,x‎2‎=‎‎−1−‎‎5‎‎2‎.‎ ‎(2)‎‎△ABC‎ 是直角三角形‎.‎ 理由如下： ∵ 方程‎(c+b)x‎2‎−2ax+c−b=0‎有两个相等的实数根， ‎∴(−2a‎)‎‎2‎−4(c+b)(c−b)=4a‎2‎−4c‎2‎+4b‎2‎=0‎， ‎∴a‎2‎−c‎2‎+b‎2‎=0‎， ‎∴a‎2‎+b‎2‎=‎c‎2‎， ∴ ‎△ABC 是直角三角形‎.‎ ‎(3)‎‎△ABC‎ 是等边三角形‎.‎ 理由如下： ‎∵a‎2‎+b‎2‎+c‎2‎=ab+ac+bc， ‎∴2a‎2‎+2b‎2‎+2c‎2‎=2ab+2ac+2bc.‎ ‎∴(a‎2‎−2ab+b‎2‎)+(b‎2‎−2bc+c‎2‎)+(a‎2‎−2ac+c‎2‎)=0‎， ‎∴(a−b‎)‎‎2‎+(b−c‎)‎‎2‎+(a−c‎)‎‎2‎=0‎， ‎∴a−b=0,b−c=0,a−c=0‎， ‎∴a=b,b=c,a=c， ‎∴a=b=c， ‎∴ △ABC是等边三角形.‎ ‎【答案】‎ ‎(1)‎证明：如图，连接OE,如图： 则 第21页 共22页 ◎ 第22页 共22页 S‎△AOE‎+S‎△BOE=‎S‎△AOB‎. ∴ ‎1‎‎2‎OA⋅EG+‎1‎‎2‎OB⋅EF=‎1‎‎2‎OA⋅BH. ∵ 四边形ABCD是矩形， ∴ OA=OC=‎1‎‎2‎AC,OB=OD=‎1‎‎2‎BD,AC=BD, ∴ OA=OB， ∴ EG+EF=BH.‎ ‎(2)‎解：‎(1)‎中的结论不成立. 理由如下：如图，连接OE, 则S‎△AEO‎−S‎△OEB=S‎△OAB,‎ ∴ ‎1‎‎2‎OA⋅EG−‎1‎‎2‎OB⋅EF=‎1‎‎2‎OA⋅BH ∵ 四边形ABCD是矩形， ∴ OA=OC=‎1‎‎2‎AC,OB=OD=‎1‎‎2‎BD,AC=BD,‎ ∴ OA=OB‎,‎ ∴ EG−EF=BH.‎ EG+EF+EH=BO ‎【考点】‎ 四边形综合题 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ ‎(1)‎证明：如图，连接OE,如图： 则S‎△AOE‎+S‎△BOE=‎S‎△AOB. ∴ ‎1‎‎2‎OA⋅EG+‎1‎‎2‎OB⋅EF=‎1‎‎2‎OA⋅BH. ∵ 四边形ABCD是矩形， ∴ OA=OC=‎1‎‎2‎AC,OB=OD=‎1‎‎2‎BD,AC=BD, ∴ OA=OB， ∴ EG+EF=BH.‎ ‎(2)‎解：‎(1)‎中的结论不成立. 理由如下：如图，连接OE, 则S‎△AEO‎−S‎△OEB=S‎△OAB,‎ ∴ ‎1‎‎2‎OA⋅EG−‎1‎‎2‎OB⋅EF=‎1‎‎2‎OA⋅BH ∵ 四边形ABCD是矩形， ∴ OA=OC=‎1‎‎2‎AC,OB=OD=‎1‎‎2‎BD,AC=BD,‎ ∴ OA=OB‎,‎ ∴ EG−EF=BH.‎ ‎(3)‎解：EG+EF+EH=BO. 理由如下： 如图，连接AE,BE,CE, 则AC⊥BD,△ABC 是等边三角形. 则S‎△ABE‎+S‎△BCE+S‎△ACE=‎S‎△ABC， ∴ ‎ 第21页 共22页 ◎ 第22页 共22页 ‎1‎‎2‎AB⋅EG+‎1‎‎2‎BC⋅EF+‎1‎‎2‎AC⋅EH=‎1‎‎2‎AC⋅BO‎， ∵ AB=AC=AC， ∴ EG+EF+EH=BO.‎ 第21页 共22页 ◎ 第22页 共22页