- 2021-11-10 发布 |
- 37.5 KB |
- 23页
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2021年中考数学压轴题专项训练 一次函数(含解析)
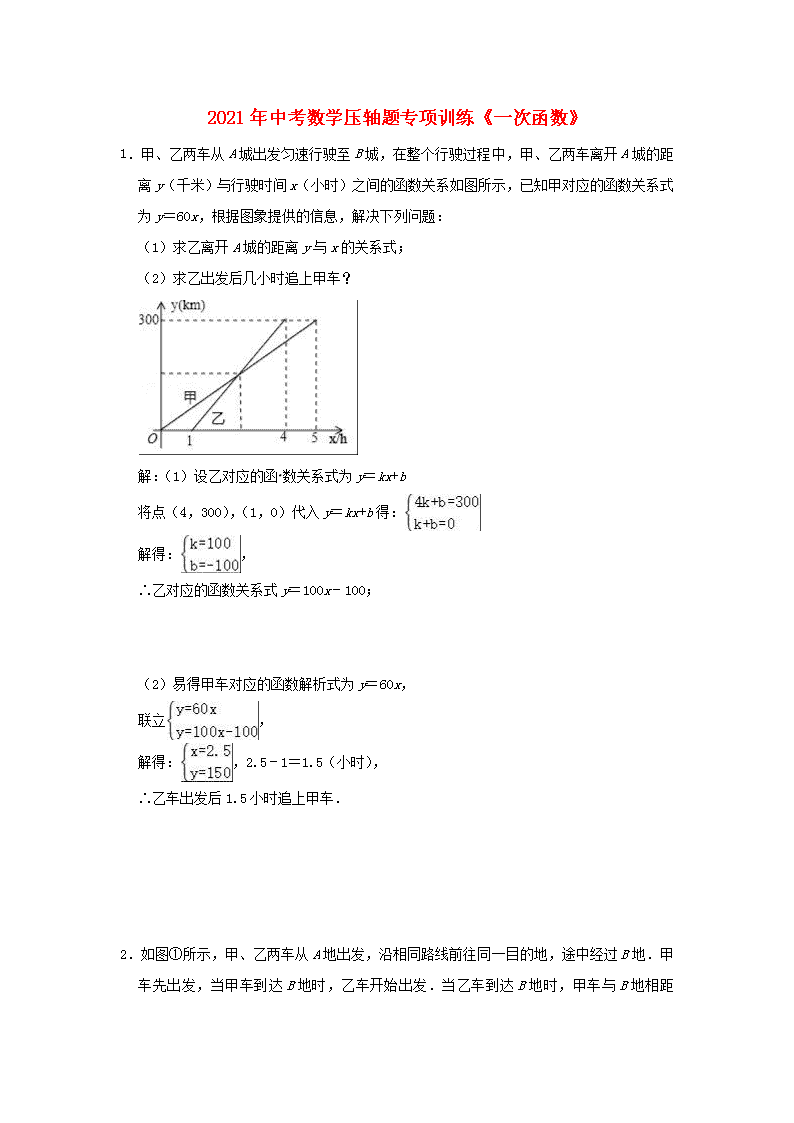
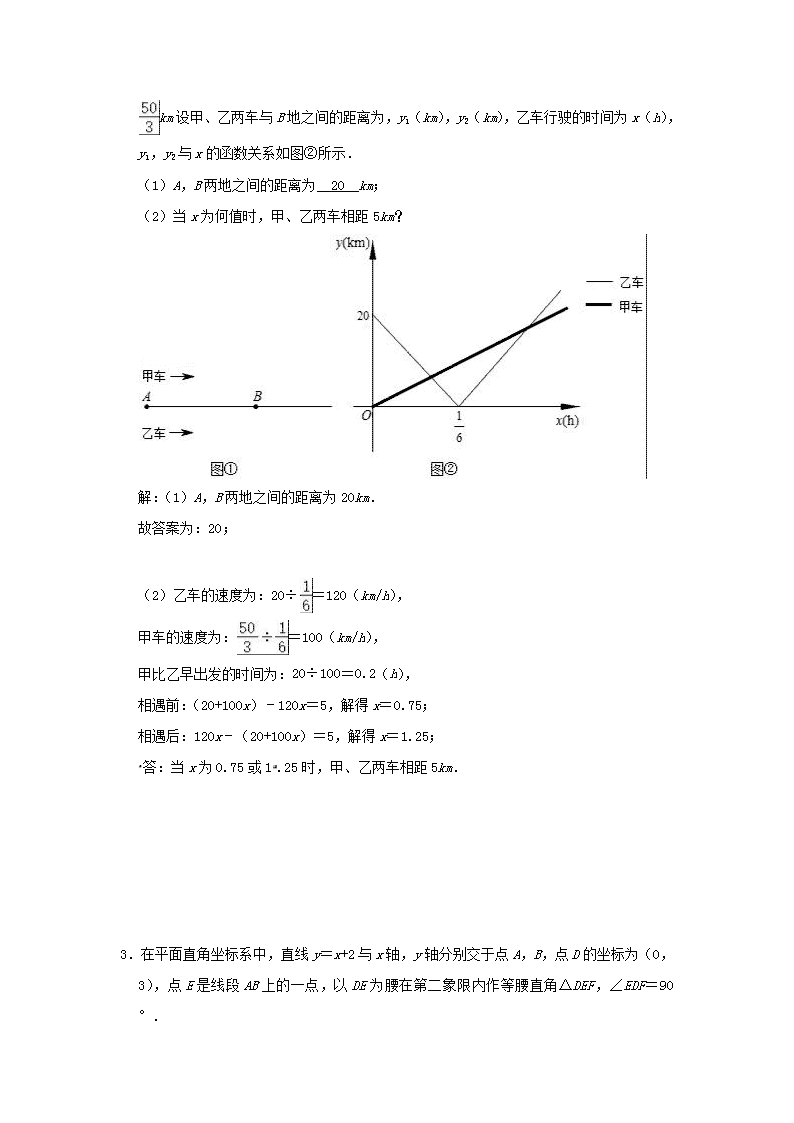
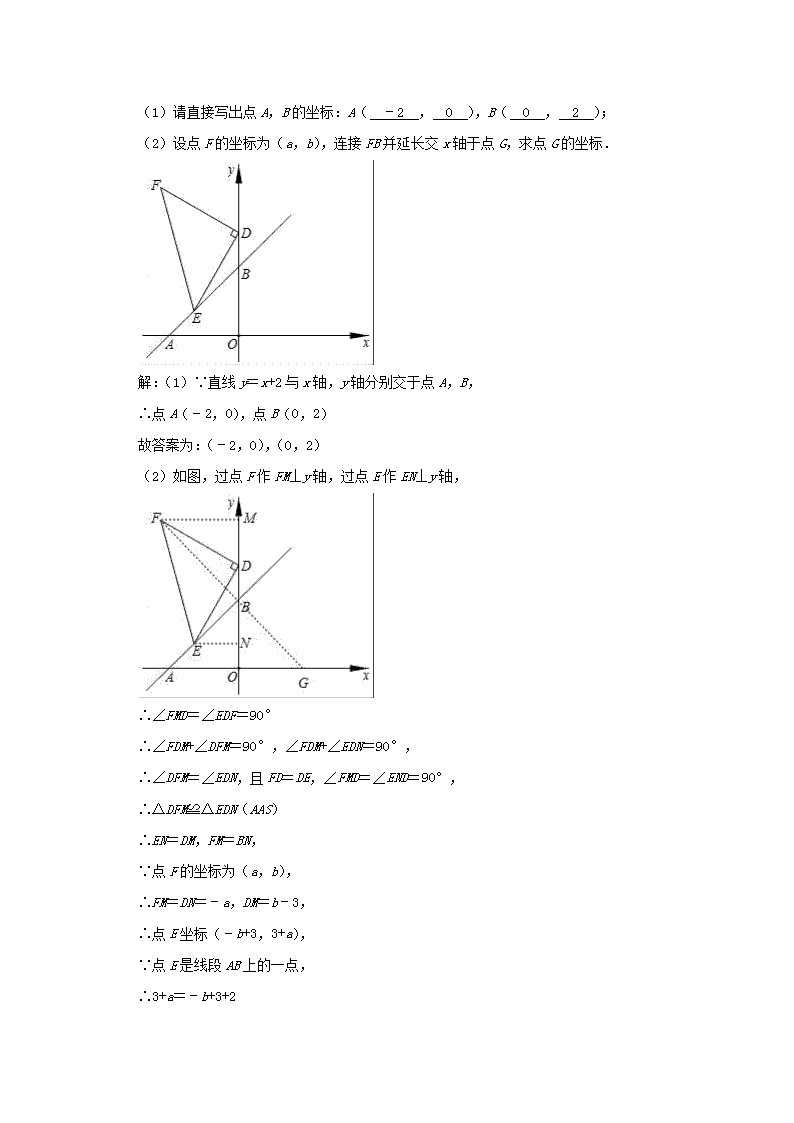
2021 年中考数学压轴题专项训练《一次函数》 1.甲、乙两车从 A 城出发匀速行驶至 B 城,在整个行驶过程中,甲、乙两车离开 A 城的距 离 y(千米)与行驶时间 x(小时)之间的函数关系如图所示,已知甲对应的函数关系式 为 y=60x,根据图象提供的信息,解决下列问题: (1)求乙离开 A 城的距离 y 与 x 的关系式; (2)求乙出发后几小时追上甲车? 解:(1)设乙对应的函 数关系式为 y=kx+b 将点(4,300),(1,0)代入 y=kx+b 得: 解得: , ∴乙对应的函数关系式 y=100x﹣100; (2)易得甲车对应的函数解析式为 y=60x, 联立 , 解得: ,2.5﹣1=1.5(小时), ∴乙车出发后 1.5 小时追上甲车. 2.如图①所示,甲、乙两车从 A 地出发,沿相同路线前往同一目的地,途中经过 B 地.甲 车先出发,当甲车到达 B 地时,乙车开始出发.当乙车到达 B 地时,甲车与 B 地相距 km 设甲、乙两车与 B 地之间的距离为,y1(km),y2(km),乙车行驶的时间为 x(h),y1, y2 与 x 的函数关系如图②所示. (1)A,B 两地之间的距离为 20 km; (2)当 x 为何值时,甲、乙两车相距 5km? 解:(1)A,B 两地之间的距离为 20km. 故答案为:20; (2)乙车的速度为:20÷ =120(km/h), 甲车的速度为: =100(km/h), 甲比乙早出发的时间为:20÷100=0.2(h), 相遇前:(20+100x)﹣120x=5,解得 x=0.75; 相遇后:120x﹣(20+100x)=5,解得 x=1.25; 答:当 x 为 0.75 或 1 .25 时,甲、乙两车相距 5km. 3.在平面直角坐标系中,直线 y=x+2 与 x 轴,y 轴分别交于点 A,B,点 D 的坐标为(0,3), 点 E 是线段 AB 上的一点,以 DE 为腰在第二象限内作等腰直角△DEF,∠EDF=90°. (1)请直接写出点 A,B 的坐标:A( ﹣2 , 0 ),B( 0 , 2 ); (2)设点 F 的坐标为(a,b),连接 FB 并延长交 x 轴于点 G,求点 G 的坐标. 解:(1)∵直线 y=x+2 与 x 轴,y 轴分别交于点 A,B, ∴点 A(﹣2,0),点 B(0,2) 故答案为:(﹣2,0),(0,2) (2)如图,过点 F 作 FM⊥y 轴,过点 E 作 EN⊥y 轴, ∴∠FMD=∠EDF=90° ∴∠FDM+∠DFM=90°,∠FDM+∠EDN=90°, ∴∠DFM=∠EDN,且 FD=DE,∠FMD=∠END=90°, ∴△DFM≌△EDN(AAS) ∴EN=DM,FM=BN, ∵点 F 的坐标为(a,b), ∴FM=DN=﹣a,DM=b﹣3, ∴点 E 坐标(﹣b+3,3+a), ∵点 E 是线段 AB 上的一点, ∴3+a=﹣b+3+2 ∴a+b=2, ∴点 F(a,2﹣a) 设直线 BF 的解析式为 y=kx+2, ∴2﹣a=ka+2 ∴k=﹣1, ∴直线 BF 的解析式为 y=﹣x+2, ∴点 G(2,0) 4.某学校甲、乙两名同学去爱国主义教育基地参观,该基地与学校相距 2400 米.甲从学校 步行去基地,出发 5 分钟后乙再出发,乙从学校骑自行车到基地.乙骑行到一半时,发 现有东西忘带,立即返回,拿好东西之后再从学校出发.在骑行过程中,乙的速度保持 不变,最后甲、乙两人同时到达基地.已知,乙骑行的总时间是甲步行时间的 .设甲 步行的时间为 x(分),图中线段 OA 表示甲离开学校的路程 y(米)与 x(分)的函数关 系的图象.图中折线 B﹣C﹣D 和线段 EA 表示乙离开学校的路程 y(米)与 x(分)的函 数关系的图象.根据图中所给的信息,解答下列问题: (1)甲步行的速度和乙骑行的速度; (2)甲出发多少时间后,甲、乙两 人第二次相遇? (3)若 s(米)表示甲、乙两人之间的距离,当 15≤x≤30 时,求 s(米)关于 x(分) 的函数关系式. 解:(1)由题意得: (米/分), =240(米/分); (2)由题意可得:C(10,1200),D(15,0),A(30,2400), 设线段 CD 的解析式为:y=kx+b,则 , 解得 ∴线段 CD 的解析式为:y=﹣240x+3600, 易知线段 OA 的解析式为:y=80x,根据题意得 240x+3600=80x, 解得:x= , ∴甲出发 分后,甲、乙两人第二次相遇; (3)∵E(20,0),A(30,2400), 设线段 EA 的解析式为:y=mx+n, , 解得 , ∴线段 EA 的解析式为:y=240x﹣4800, ∴当 15≤x≤20 时,s=yOA﹣0=80x, 当 20<x≤30 时,s=yOA﹣yEA=80x﹣(240x﹣4800)=﹣160x+4800, ∴ . 5.对于给定的△ABC,我们给出如下定义: 若点 M 是边 BC 上的一个定点,且以 M 为圆心的半圆上的所有点都在△ABC 的内部或边上, 则称这样的半圆为 BC 边上的点 M 关于△ABC 的内半圆,并将半径最大的内半圆称为点 M 关于△ABC 的最大内半圆. 若点 M 是边 BC 上的一个动点(M 不与 B,C 重合),则在所有的点 M 关于△ABC 的最大内 半圆中,将半径最大的内半圆称为 BC 关于△ABC 的内半圆. (1)在 Rt△ABC 中,∠BAC=90°,AB=AC=2, ①如图 1,点 D 在边 BC 上,且 CD=1,直接写出点 D 关于△ABC 的最大内半圆的半径长; ②如图 2,画出 BC 关于△ABC 的内半圆,并直接写出它的半径长; (2)在平面直角坐标系 xOy 中,点 E 的坐标为(3,0),点 P 在直线 y= x 上运动(P 不与 O 重合),将 OE 关于△OEP 的内半圆半径记为 R,当 ≤R≤1 时,求点 P 的横坐标 t 的取值范围. 解:(1)①如图 1,过 D 作 DE⊥AC 于 E, ∵Rt△ABC 中,∠BAC=90°,AB=AC=2, ∴∠C=∠B=45°, ∵CD=1, ∴BD=2 ﹣1>CD, ∴D 到 AC 的距离小于到 AB 的距离, ∵△DEC 是等腰直角三角形, ∴DE= , 即点 D 关于△ABC 的最大内半圆的半径长是 ; ②当 D 为 BC 的中点时,BC 关于△ABC 的内半圆为⊙D,如图 2, ∴BD= BC= , 同理可得:BC 关于△ABC 的内半圆半径 DE=1. (2)过点 E 作 EF⊥OE,与直线 y= x 交于点 F,设点 M 是 OE 上的动点, i)当点 P 在线段 OF 上 运动时(P 不与 O 重合),OE 关于△OEP 的内半圆是以 M 为圆心, 分别与 OP,PE 相切的半圆,如图 3,连接 PM, ∵直线 OF:y= x ∴∠FOE=30° 由(1)可知:当 M 为线段中点时,存在 OE 关于△OEP 的内半圆, ∴当 R= 时,如图 3,DM= ,此时 PM⊥x 轴,P 的横坐标 t=OM= ; 如图 4,当 P 与 F 重合时,M 在∠EFO 的角平分线上,⊙M 分别与 OF,FE 相切, 此时 R=1,P 的横坐标 t=OE=3; ∴当 ≤R≤1 时,t 的取值范围是 ≤t≤3. ii)当点 P 在 OF 的延长线上运动时,OE 关于△OEP 的内半圆是以 M 为圆心,经过点 E 且 与 OP 相切的半圆,如图 5. ∴当 R=1 时,t 的取值范围是 t≥3. iii)当点 P 在 OF 的反向延长上运动时(P 不与 O 重合),OE 关于△OEP 的内半圆是以 M 为圆心,经过点 O 且与 EP 相切的半圆,如图 6. ∵∠FOE=∠OPE+∠OEP=30°, ∴∠OEP<30°, ∴OM<1, 当 R= 时,如图 6,过 P 作 PA⊥x 轴于 A,N 是切点,连接 MN,MN⊥PE,此时 OM=MN= ,ME=3﹣ = , ∴EN= = = , Rt△OPA 中,∠POA=30°,OA=﹣t, ∴PA=﹣ t, ∵∠ENM=∠EAP=90°,∠MEN=∠AEP, ∴△EMN∽△EPA, ∴ ,即 = 解得:t=﹣ , ∴当 ≤R<1 时,t 的取值范围是 t≤﹣ . 综上,点 P 在直线 y= x 上运动时(P 不与 O 重合),当 ≤R≤1 时,t 的取值范围是 t≤﹣ 或 t≥ . 6.已知,一次函数 y=﹣ x+6 的图象与 x 轴、y 轴分别交于点 A、点 B,与直线 y= x 相 交于点 C.过点 B 作 x 轴的平行线 l.点 P 是直线 l 上的一个动点. (1)求点 A,点 B 的坐标. (2)若 S△AOC=S△BCP,求点 P 的坐标. (3)若点 E 是直线 y= x 上的一个动点,当△APE 是以 AP 为直角边的等腰直角三角形 时,求点 E 的坐标. 解:(1)一次函数 y=﹣ x+6 的图象与 x 轴、y 轴分别交于点 A、点 B, 则点 A、B 的坐标分别为:(8,0)、(0,6); (2)联立 y=﹣ x+6、y= x 并解得:x=3,故点 C(3, ), S△AOC= 8× =15=S△BCP= BP×(yP﹣yC)= BP×(6﹣ ), 解得:BP= , 故点 P( ,6)或(﹣ ,6) (3)设点 E(m, m)、点 P(n,6); ①当∠EPA=90°时,如左图, ∵∠MEP+∠MPE=90°,∠MPE+∠NPA=90°, ∴∠MEP=∠NPA,AP=PE,∵△EMP≌△PNA(AAS), 则 ME=PN=6,MP=AN, 即|m﹣n|=6, m﹣6=8﹣n, 解得:m= 或 16, 故点 E( , )或(14, ); ②当∠EAP=90°时,如右图, 同理可得:△AMP≌△ANE(AAS), 故 MP=EN,AM=AN=6, 即 m=n﹣8,|8﹣m|=6,解得:m=2 或 14, 故点 E(2, )或(16,20); 上,E( , )或(14, )或;(2, )或(16,20). 7.如图,A,B 是直线 y=x+4 与坐标轴的交点,直线 y=﹣2x+b 过点 B,与 x 轴交于点 C. (1)求 A,B,C 三点的坐标; (2)当点 D 是 AB 的中点时,在 x 轴上找一点 E,使 ED+EB 的和最小,画出点 E 的位置, 并求 E 点的坐标. (3)若点 D 是折线 A﹣B﹣C 上一动点,是否存在点 D,使 AACD 为直角三角形,若存在, 直接写出 D 点的坐标;若不存在,请说明理由. 解:(1)在 y=x+4 中, 令 x=0,得 y=4, 令 y=0,得 x=﹣4,∴A(﹣4,0),B(0,4). 把 B(0,4)代入,y=﹣2x+b, 得 b=4 ∴直线 BC 为:y=﹣2x+4. 在 y=﹣2x+4 中, 令 y=0,得 x=2, ∴C 点的坐标为(2,0); (2)如图点 E 为所求 点 D 是 AB 的中点,A(﹣4,0),B(0,4).∴D(﹣2,2). 点 B 关于 x 轴的对称点 B1 的坐标为(0,﹣4). 设直线 DB1 的解析式为 y=kx+b. 把 D(﹣2,2),B1(0,﹣4)代入一次函数表达式并解得: 故该直线方程为:y=﹣3x﹣4. 令 y=0,得 E 点的坐标为 . (3)存在,D 点的坐标为(﹣1,3)或 . ①当点 D 在 AB 上时,由 OA=OB=4 得到:∠BAC=45°, 由等腰直角三角形求得 D 点的坐标为(﹣1,3); ②当点 D 在 BC 上时,如图,设 AD 交 y 轴于点 F. 在△AOF 与△BOC 中,∠FAO=∠CBO,∠AOF=∠BOD,AO=BO, ∴△AOF≌△BOC(ASA).∴OF=OC=2, ∴点 F 的坐标为(0,2), 易得直线 AD 的解析式为 ,与 y=﹣2x+4 组成方程组并解得: x= ,∴交点 D 的坐标为 . 8.(1)模型建立: 如图 1,等腰直角三角形 ABC 中,∠ACB=90°,CB=CA,直线 ED 经过点 C,过 A 作 AD ⊥ED 于 D,过 B 作 BE⊥ED 于 E.求证:△BEC≌△CDA; (2)模型应用: ①如图 2,一次函数 y=﹣2x+4 的图象分别与 x 轴、y 轴交于点 A、B,以线段 AB 为腰在 第一象限内作等腰直角三角形 ABC,则 C 点的坐标为 C(4,6)或 C(6,2) (直接 写出结果) ②如图 3,在△ABC 和△DCE 中,CA=CB,CD=CE,∠CAB=∠CED=45°,连接 BD、AE, 作 CM⊥AE 于 M 点,延长 MC 与 BD 交于点 N,求证:N 是 BD 的中点. 解:(1)∵AD⊥ED,BE⊥ED, ∴∠D=∠E=90°,∠ACD=∠CAD=90°, ∵∠ACB=90°, ∴∠ACD=∠BCE=90°, ∴∠BCE=∠CAD, 在△BEC 和△CDA 中 , ∴△BEC≌△CDA(AAS); (2)①根据题意可得点 C 的坐标为 C(4,6)或 C(6,2); 故答案为: C(4,6)或 C(6,2); ②如图,作 BP⊥MN 交 MN 的延长线于 P,作 DQ⊥MN 于 Q ∵∠BCP+∠BCA=∠CAM+∠AMC, ∵∠BCA=∠AMC, ∴∠BCP=∠CAM, 在△CBP 与△ACM 中, , ∴△CBP≌△ACM(AAS), ∴MC=BP, 同理,CM=DQ, ∴DQ=BP 在△BPN 与△DQN 中, , ∵△BPN≌△DQN(AAS), ∴BN=ND, ∴N 是 BD 的中点. 9.如图,在平面直角坐标系 xOy 中,直线 l:y=﹣ x+4 与 x 轴、y 轴分别相交于 B、A 两 点,点 C 是 AB 的中点,点 E、F 分别为线段 AB、OB 上的动点,将△BEF 沿 EF 折叠,使点 B 的对称点 D 恰好落在线段 OA 上(不与端点重合).连接 OC 分别交 DE、DF 于点 M、N, 连接 FM. (1)求 tan∠ABO 的值; (2)试判断 DE 与 FM 的位置关系,并加以证明; (3)若 MD=MN,求点 D 的坐标. 解:(1)直线 l:y=﹣ x+4 与 x 轴、y 轴分别相交于 B、A 两点, 则点 A、B 的坐标分别为:(0,4)、(3,0); tan∠ABO= = =tanα; (2)DE 与 FM 的位置关系为相互垂直,理由: 点 C 是 AB 的中点, 则∠COB=∠CBO=∠EDF=α,∠ONF=∠DNM, ∴∠DMN=∠DFO, ∴O、F、M、D 四点共圆, ∴∠DMF+∠DOF=180°, ∴∠DOF=90°,即:DE⊥FM; (3)MD=MN, ∴∠MDN=∠MND=α, 而∠COB=α,∠DNM=∠ONF=α, 即△OCF 为以 ON 为底,底角为α的等腰三角形, 则 tan∠NFO= = =tanβ,则 cosβ= (证明见备注); 设 OF=m,则 DF=FB=3﹣m, cos∠DFO=cosβ= , 解得:m= , OD2=DF2﹣OF2=(3﹣m)2﹣m2= ; 则 OD= , 故点 D(0, ). 备注:如下图, 过点 N 作 HN⊥OF 于点 H,tanα= ,则 sinα= ,作 FM⊥ON 于点 M, 设 FN=OF=5a,则 FN=4a,则 ON=6a, 同理可得:NH= , tan∠NFO= = =tanβ,则 cosβ= . 10.如图,直线 l1:y= x+ 与 y 轴的交点为 A,直线 l1 与直线 l2:y=kx 的交点 M 的坐标 为 M(3,a). (1)求 a 和 k 的值; (2)直接写出关于 x 的不等式 x+ <kx 的解集; (3)若点 B 在 x 轴上,MB=MA,直接写出点 B 的坐标. 解:(1)∵直线 l1 与直线 l2 的交点为 M(3,a), ∴M(3,a)在直线 y= x+ 上,也在直线 y=kx 上, ∴a= ×3+ =3, ∴M(3,3), ∴3=3k, 解得 k=1; (2)不等式 x+ <kx 的解集为 x>3; (3)作 MN⊥x 轴于 N, ∵直线 l1:y= x+ 与 y 轴的交点为 A, ∴A(0, ), ∵M(3,3), ∴AM2=(3﹣0)2+(3﹣ )2= , ∵MN=3,MB=MA, ∴BN= = , ∴B( ,0)或 B( ,0). 11.如图,长方形 OBCD 的 OB 边在 x 轴上,OD 在 y 轴上,把 OBC 沿 OC 折叠得到 OCE,OE 与 CD 交于点 F. (1)求证:OF=CF; (2)若 OD=4,OB=8,写出 OE 所在直线的解析式. 解:(1)∵四边形 OBCD 为矩形, ∴DO=BC,∠OBC=∠ODC. 由翻折的性质可知∠E=∠OBC,CE=BC, ∴OD=CE,∠E=∠ODC. 在△ODF 和△CEF 中, ∴△ODF≌△CEF(AAS), ∴OF=CF. (2)∵OF=CF. 设 DF=x,则 OF=CF=8﹣x. 在 Rt△ODF 中,OD=4,根据勾股定理得,OD2+DF2=OF2, ∴42+x2=(8﹣x)2, 解得 x=3, ∴F(3,4), 设直线 OE 的解析式为 y=kx, 把 F(3,4)代入得 4=3k, 解得 k= , ∴OE 所在直线的解析式 y= x. 12.如图,在平面直角坐标系中,直线 y=﹣x+m 过点 A(5,﹣2)且分别与 x 轴、y 轴交于 点 B、C,过点 A 画 AD∥x 轴,交 y 轴于点 D. (1)求点 B、C 的坐标; (2)在线段 AD 上存在点 P,使 BP +CP 最小,求点 P 的坐标. 解:(1)∵y=﹣x+m 过点 A(5,﹣2), ∴﹣2=﹣5+m, ∴m=3, ∴y=﹣x+3, 令 y=0,∴x=3, ∴B(3,0), 令 x=0,∴y=3, ∴C(0,3); (2)过 C 作直线 AD 对称点 Q, 可得 Q(0,﹣7), 连结 BQ,交 AD 与点 P 可得直线 BQ: , 令 y′=﹣2, ∴ , ∴ . 13.如图,直线 l1 的函数表达式为 y=3x﹣2,且直线 l1 与 x 轴交于点 D.直线 l2 与 x 轴交 于点 A,且经过点 B(4,1),直线 l1 与 l2 交于点 C(m,3). (1)求点 D 和点 C 的坐标; (2)求直线 l2 的函数表达式; (3)利用函数图象写出关于 x,y 的二元一次方程组 的解. 解:(1)在 y=3x﹣2 中 令 y=0,即 3x﹣2=0 解得 x= , ∴D( ,0), ∵点 C(m,3)在直线 y=3x﹣2 上, ∴3m﹣2=3, ∴m= , ∴C( ,3); (2)设直线 l2 的函数表达式为 Y=KX+B(K≠0), 由题意得: , 解得: , ∴y=﹣ x+ ; (3)由图可知,二元一次方程组 的解为 . 14.如图,在平面直角坐标系中,一次函数 y=kx+b 的图象与 x 轴交于点 A(﹣3,0),与 y 轴交于点 B,且与正比例函数 y= x 的图象交点为 C(m,4). (1)求一次函数 y=kx+b 的解析式; (2)求△BOC 的面积; (3)若点 D 在第二象限,△DAB 为等腰直角三角形,则点 D 的坐标为 (﹣2,5)或(﹣ 5,3)或( , ) . 解:(1)∵点 C 在正比例函数图象上, ∴ m=4,解得:m=3, ∵点 C(3,4)、A(﹣3,0)在一次函数图象上, ∴代入一次函数解析式可得 ,解这个方程组得 , ∴一次函数的解析式为 y= x+2; (2)在 中,令 x=0,解得 y=2, ∴B(0,2) ∴S△BOC=×2×3=3; (3)过点 D1 作 D1E⊥y 轴于点 E,过点 D2 作 D2F⊥x 轴于点 F,如图, ∵点 D 在第二象限,△DAB 是以 AB 为直角边的等腰直角三角形, ∴AB=BD2, ∵∠D1BE+∠ABO=90°,∠ABO+∠BAO=90°, ∴∠BAO=∠EBD1, ∵在△BED1 和△AOB 中, ∴△BED1≌△AOB(AAS), ∴BE=AO=3,D1E=BO=2, 即可得出点 D 的坐标为(﹣2,5); 同理可得出:△AFD2≌△AOB, ∴FA=BO=2,D2F=AO=3, ∴点 D 的坐标为(﹣5,3), ∵∠D1AB=∠D2BA=45°, ∴∠AD3B=90°, ∴D3( , ), 综上可知点 D 的坐标为(﹣2,5)或(﹣5,3)或( , ). 故答案为:(﹣2,5)或(﹣5,3)或( , ). 15.如图 1 中的三种情况所示,对于平面内的点 M,点 N,点 P,如果将线段 PM 绕点 P 顺时 针旋转 90°能得到线段 PN,就称点 N 是点 M 关于点 P 的“正矩点”. (1)在如图 2 所示的平面直角坐标系 xOy 中,已知 S(﹣3,1),P(1,3),Q(﹣1,﹣ 3),M(﹣2,4). ①在点 P,点 Q 中, 点 P 是点 S 关于原点 O 的“正矩点”; ②在 S,P,Q,M 这四点中选择合适的三点,使得这三点满足: 点 S 是点 P 关于点 M 的“正矩点”,写出一种情况即可; (2)在平面直角坐标系 xOy 中,直线 y=kx+3(k<0)与 x 轴交于点 A,与 y 轴交于点 B, 点 A 关于点 B 的“正矩点”记为点 C,坐标为 C(xc,yc). ①当点 A 在 x 轴的正半轴上且 OA 小于 3 时,求点 C 的横坐标 xc 的值; ②若点 C 的纵坐标 yc 满足﹣1<yc≤2,直接写出相应的 k 的取值范围. 解:(1)①在点 P,点 Q 中,点 S 绕点 O 顺时针旋转 90°能得到线段 OP,故 S 关于点 O 的“正矩点”为点 P, 故答案为点 P; ②点 S 是点 P 关于点 M 的“正矩点”(答案不唯一); 故 答案为:S,P,M; (2)①如图 1,作 CE⊥x 轴于点 E,作 CF⊥y 轴于点 F, ∠BFC=∠AOB=90°,点 B(0,3),点 A(﹣ ,0), ∵∠ABO+∠CBO=90°,∠CBO+∠BCF=90°, ∴∠BCF=∠ABO,BC=BA, ∴△BCF≌△AOB(AAS), ∴FC=OB=3, 故点 C 的坐标为:(﹣3,3+ ), 即点 C 的横坐标 xc 的值为﹣3; ②点 C(﹣3,3+ ),如图 2, ﹣1<yc≤2,即:﹣1<3+ ≤2, 则﹣3≤k .查看更多