苏科版九年级上册期中考试数学试题（苏教版九年级数学上册期中考试测试卷）

苏科版九年级上册期中考试数学试题（苏教版九年级数学上册期中考试测试卷）

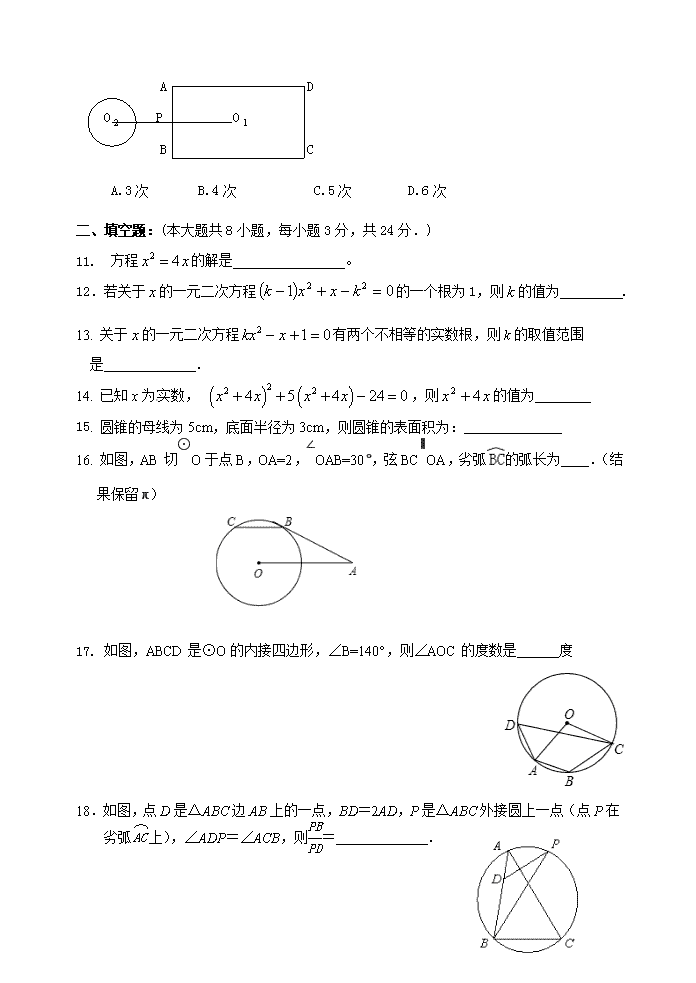
苏教版九年级数学上册期中考试测试卷 一、选择题：（本大题共 10 小题，每小题 3分，共 30 分） 1．下列关于 x 的方程中，一定是一元二次方程的是（ ） A． 02  cbxax B． 2)1()3)(2(  xxx C． 012 x D． 11  xx 2．下列四个命题：①直径所对的圆周角是直角；②圆既是轴对称图形，又是中心对称 图形；③在同圆中，相等的圆周角所对的弦相等；④三点确定一个圆．其中正确命题 的个数为 ( ) A ．1 B．2 C．3 D．4 3．方程 x2＋3＝4x 用配方法解时，应先化成 （ ） A．(x－2)2＝7 B．(x＋2)2＝1 C．(x＋2)2＝2 D．(x－2)2＝1 4. 已知关于 x 的一元二次方程 x2－3x+2=0 两实数根为 x1、x2，则 x1+x2=（ ） A.3 B.-3 C.1 D.-1 5．已知 m 是方程 2 1 0x x   的一 个根，则代数式 2m m 的值等于 ( ) A. 1 B. －1 C. 0 D. 2 6. 在平面直角坐标系中，以点（2，3）为圆心，2 为半径的圆必定（ ） A．与 x 轴相离、与 y 轴相切 B．与 x 轴、y 轴都相离 C．与 x 轴相切、与 y 轴相离 D．与 x 轴、y 轴都相切 7. 为了让某市的山更绿、水更清，2014 年市委、市政府提出了 确保到 2016 年实现全 市森林覆盖率达到 63%的目标，已知 2014 年该市森林覆盖率为 60 %，设从 2014 年 起森林覆盖率的年平均增长率为 x ，则可列方程 ( ) A．  60 1 2 63%x  B．  60 1 2 63x  C．  260 1 63%x  D．  260 1 63x  8. 如图，⊙O 是△ABC 的外接圆，∠BOC＝100°，则∠A 的度数 等于 （ ） A．60° B．50° C．40° D．30° 9. 如右图，在 中， ， ， ， 以 点 为圆心， 为半径的圆与 交于点 ，则 的长为( ) A. B. C. D. 10.如图，矩形 ABCD 的长为 6，宽为 3，点 O 1 为矩形的中心，⊙O 2 的半径为 1，O 1 O 2 ⊥ AB 于点 P, O 1 O 2 =6.若⊙O 2 绕点 P 按顺时针方向旋转 360°，在旋转过程中，⊙O 2 与矩 形的边只有一个公共点的情况一共出现 （ ） C A D B A D O 2 P O 1 B C A.3 次 B.4 次 C.5 次 D.6 次 二、填空题：(本大题共 8 小题，每小题 3 分，共 24 分．) 11. 方程 2 4x x 的解是 。 12．若关于 x 的一元二次方程  01 22  kxxk 的一个根为 1，则 k 的值为 . 13. 关于 x 的一元二次方程 2 1 0kx x   有两个不相等的实数根，则 k 的取值范围 是 ． 14. 已知 x 为实数，    22 24 5 4 24 0x x x x     ，则 xx 42  的值为 15. 圆锥的母线为 5cm，底面半径为 3cm，则圆锥的表面积为： 16. 如图，AB 切⊙O 于点 B，OA=2，∠OAB=30°，弦 BC∥OA，劣弧 的弧长为 ．（结 果保留π） 17. 如图，ABCD 是⊙O 的内接四边形，∠B=140°，则∠AOC 的度数是 度 18．如图，点 D 是△ABC 边 AB 上的一点，BD＝2AD，P 是△ABC 外接圆上一点（点 P 在劣弧 ⌒AC上），∠ADP＝∠ACB，则PB PD ＝ ． A BO C D 三、解答题：（本大题共 76 分。解答时应写出必要的计算过程、推演步骤或文字说明） 19.（5 分）解方程： (x－1)2＝9 20.（5 分） 解方程： 2 4 621 0x x   21.（5 分） 解方程： 2 4 1 1 3 x x x    22．( 6 分) 关于 x 的一元二次方程 2 (3 1) 1 2mx m x m    ,其根的判别式的值为 1, 求 m 的值及该方程的根. 23.（6 分）如图，AB 是⊙O 的直径，⌒AC ＝⌒CD ，∠COD＝60°． 求证：⑴△AOC 是等边三角形； ⑵OC∥BD． 24.（8 分）已知关于 x 的一元二次方程 022  mxx 有两个实数根． ⑴ 求 m 的范围； ⑵若方程两个实数根为 1x 、 2x ，且 1x +3 2x =8，求 m 的值． P E O A B C 25. (8 分) 已知△ABC 的一条边 BC 的长为 5， 另两边 AB、AC 的长是关 于 x 的一元 二次方程   0332  kxkx 的两个实数根． （1）求证：无论 k 为何值时，方程总有两个实数根； （2）当△ABC 是等腰三角形时，求 k 的值． 26． (8 分) 如图，点 A 、 B 、C 是⊙O 上的三点， //AB OC ． （1）求证： AC 平分 OAB ． （2）过点O 作OE AB 于点 E ，交 AC 于点 P ． 若 2AB  ， 30AOE   ，求OE 的长． 27. （8 分）某特产专卖店销售“红心柚”，已知“红心柚”的进价为每个 10 元，现在的售价 是每个 16 元，每天可卖出 120 个. 市场调查反映：如调整价格，每涨价 1 元，每天要 少卖出 10 个；每降价 1 元，每天可多卖出 30 个. （1）如果专卖店每天要想获得 770 元的利润，且要尽可能的让利给顾客，那么售价应 涨价多少元？ （2）请你帮专卖店老板算一算，如何定价才能使利润最大，并求出此时的最大利润？ 28．(8 分）如图⊙O 是△ABC 的外接圆，∠ABC＝45°，延长 BC 于 D，连接 AD，使得 AD∥OC, AB 交 OC 于 E. (1)求证：AD 与⊙O 相切； (2)若 AE=2 5 CE=2. 求⊙O 的半径和 AB 的长度. 29．（10 分）如图，平面直角坐标系 xOy 中，一次函数 y=﹣ x+b（b 为常数， b＞0）的图象与 x 轴、y 轴分别相交于点 A、B，半径为 4 的⊙O 与 x 轴正半轴相交于点 C，与 y 轴相交于点 D、E，点 D 在点 E 上方． （1）若直线 AB 与 有两个点 F、G． ①求∠CFE 的度数； ②用含 b 的代数式表示 FG2，并直接写出 b 的取值范围； （2） 设 b≥5，在线段 AB 上是否存在点 P，使∠CPE=45°？若存在，请求出 P 点坐标；若不存在，请说明理由． O A D B CE