呼和浩特专版2020中考数学复习方案第四单元三角形第16课时几何初步及平行线相交线课件

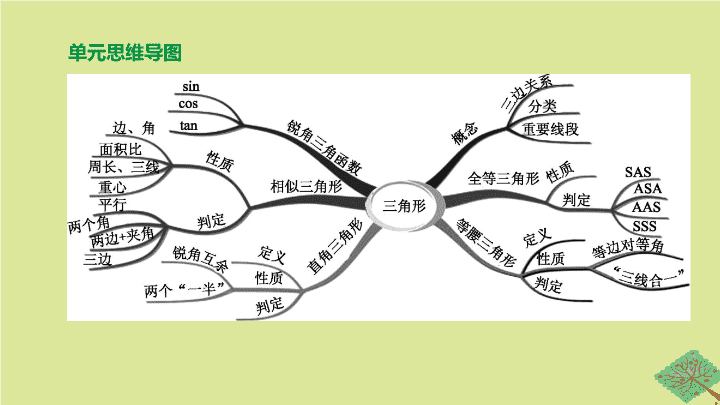
呼和浩特专版2020中考数学复习方案第四单元三角形第16课时几何初步及平行线相交线课件

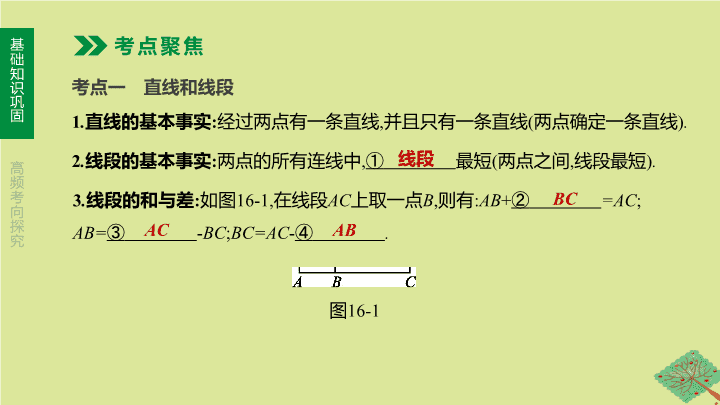
单元思维导图 第 16 课时 几何初步及平行线、相交线 第四单元　三角形 考点一　直线和线段 考点聚焦 1 . 直线的基本事实 : 经过两点有一条直线 , 并且只有一条直线 ( 两点确定一条直线 ) . 2 . 线段的基本事实 : 两点的所有连线中 , ① 　　　　 最短 ( 两点之间 , 线段最短 ) .  3 . 线段的和与差 : 如图 16-1, 在线段 AC 上取一点 B , 则有 : AB + ② 　　　　 =AC ; AB= ③ 　　　　 - BC ; BC=AC - ④ 　　　　 .  图 16-1 线段 BC AC AB 图 16-2 5 . 两点间的距离 : 连接两点间的线段的长度 . MB 考点二　相交线 1 . 三线八角 ( 如图 16-3) (1) 对顶角 性质 : 对顶角相等 . 举例 : ∠ 1 与∠ 3, ∠ 2 与∠ 4, ∠ 5 与∠ 7, ∠ 6 与 ⑥ 　　　　 .  (2) 邻补角 性质 : 互为邻补角的两个角之和等于 180° . 举例 : ∠ 1 与∠ 2 、∠ 4, ∠ 2 与∠ 1 、∠ 3, ∠ 8 与∠ 5 、∠ 7, ∠ 7 与∠ 6 、∠ 8 等 . (3) 同旁内角 举例 : ∠ 2 与∠ 5, ∠ 3 与 ⑦ 　　　　 .  图 16-3 ∠ 8 ∠ 8 (4) 同位角 举例 : ∠ 1 与 ⑧ 　　　　 , ∠ 2 与∠ 6, ∠ 4 与∠ 8, ∠ 3 与∠ 7 .  (5) 内错角 举例 : ∠ 2 与 ⑨ 　　　　 , ∠ 3 与∠ 5 .  图 16-3 ∠ 5 ∠ 8 2 . 垂线 (1) 在同一平面内 , 过一点有且只有 ⑩ 　　　 条直线与已知直线垂直 .  (2) 连接直线外一点与直线上各点的所有线段中 , ⑪ 　　　　 最短 . 简单说成 : 垂线段最短 .  (3) 点到直线的距离 : 直线外一点到这条直线的 ⑫ 　　 　 的长度 , 叫做点到直线的距离 . 如图 16-4, 点 P 与直线 l 上各点连接的所有线段中 , PB 最短 , 点 P 到直线 l 的距离是 PB 的长度 .  图 16-4 一 垂线段 垂线段 考点三　角 量角器的 使用 　 量角器的中心和角的顶点对齐 , 量角器的零刻度线和角的一条边对齐 , 做到两对齐后看角的另一边与刻度线对应的度数 度 分秒的 换算 　 1 周角 = 360°,1 平角 = 180 °,1 ° = ⑬ 　　　　 ' ,1 '= ⑭ 　　　　 ″  两角 间的 关系 互余 　 α + β= ⑮ 　　　　 ⇔ α , β 互为余角   　 同角 ( 等角 ) 的余角 ⑯ 　　　   互补 　 α + β= ⑰ 　　 　 ⇔ α , β 互为补角   　 同角 ( 等角 ) 的补角 ⑱ 　　　   角平分线 　 一般地 , 从一个角的顶点出发 , 把这个角分成两个相等的角的射线 , 叫做这个角的平分线 60 60 90° 相等 180° 相等 考点四　平行线的性质与判定 1 . 平行公理 经过直线外一点 , 有且只有 ⑲ 　　　　 条直线与这条直线平行 .  2 . 平行公理的推论 如果两条直线都与第三条直线平行 , 那么这两条直线也 ⑳ 　 　　 .  一 互相平行 3 . 平行线的性质和判定 图 16-5 相等 ∠ 2 相等 a ∥ b 互补 180° 4 . 两平行线间的距离 (1) 定义 : 两条平行线中 , 一条直线上任意一点到另一条直线的 ㉗ 　　　 , 叫做这两条平行线之间的距离 .  (2) 性质 : 两条平行线之间的距离处处 ㉘ 　　　　 .  距离 相等 题组一　必会题 对点演练 [ 答案 ] (1)54 　 18 　 54 . 3 　 144 　 18 　 144 . 3 [ 解析 ] ∠ α 的余角为 90°- ∠ α= 90°-35°42 '= 54°18 ' , ∵ 18 '= 0 . 3°, ∴ 54°18 '= 54 . 3° . ∠ α 的补角是 180°-35°42 '= 144°18 ' , ∵ 18 '= 0 . 3°, ∴ 144°18 '= 144 . 3° . [ 答案 ] (2)65° 　 [ 解析 ] 设这个角为 x °, 则 180- x= 4(90- x )+15, ∴ x= 65 . [ 答案 ] (3)23°5 ' 20 ″ 2 . 如图 16-6, 直线 AB 与 CD 相交于点 O , 若∠ 1+ ∠ 2 = 80°, 则∠ 3 的度数为 　　　　 .  图 16-6 140° 3 . [ 七下 P23 习题 5 . 3 第 4 题改编 ] 如图 16-7, a ∥ b , c , d 是截线 , 若∠ 1 = 80°, ∠ 5 = 70°, 则∠ 2 = 　　　　 , ∠ 3 = 　　　　 , ∠ 4 = 　　　　 .  图 16-7 [ 答案 ] 80° 　 110° 　 110° 　 [ 解析 ] ∵ a ∥ b , ∴∠ 2 = ∠ 1 = 80°( 两直线平行 , 内错角相等 ), ∠ 3 = 180°- ∠ 5 = 180°-70° = 110°( 两直线平行 , 同旁内角互补 ), ∠ 4 = ∠ 3 = 110°( 两直线平行 , 同位角相等 ) . 4 . [ 八上 P17 习题 11 . 2 第 6 题改编 ] 如图 16-8, AB ∥ CD , ∠ A= 45°, ∠ C= ∠ E , 则∠ C= 　　　　 .  22.5° 图 16-8 [ 答案 ] 1 题组二　易错题 【 失分点 】 不能正确分辨两直线被第三条直线所截形成的位置角 ; 图形位置不明确时忽视分类讨论的数学思想 . 6 . 如图 16-9, 下列说法错误的是 ( 　　 ) A . ∠ C 与∠ 1 是内错角 B . ∠ 2 与∠ 3 是内错角 C . ∠ A 与∠ B 是同旁内角 D . ∠ A 与∠ 3 是同位角 图 16-9 [ 答案 ] B 　 [ 解析 ] ∠ 2 与∠ 3 不是两条直线被第三条直线所截形成的位置角 , 它们构成平角 , 是邻补角 . 7 . 已知点 A , B , C 都是直线 l 上的点 , 且 AB= 5 cm, BC= 3 cm, 那么点 A 与点 C 之间的距离是 　　 　　 .  8 cm 或 2 cm [ 答案 ] 105° 或 35° 　 [ 解析 ] ∵∠ AOB= 35°, ∠ AOC= 2 ∠ AOB , ∴∠ AOC= 70°, 当 OC , OA 在 OB 同侧时 , ∠ BOC= ∠ AOC + ∠ AOB= 105°; 当 OC , OA 在 OB 异侧时 , ∠ BOC= ∠ AOC - ∠ AOB= 35° . 8 . 已知∠ AOB= 35°, 以 O 为顶点作射线 OC , 若∠ AOC= 2 ∠ AOB , 则∠ BOC= 　　　　 ° .  考向　平行线的性质及判定 例 [2019· 鄂州 ] 如图 16-10, 一块直角三角尺的一个顶点落在直尺的一边上 , 若∠ 2 = 35°, 则∠ 1 的度数为 ( 　　 ) A . 45° B . 55° C . 65° D . 75° 图 16-10 [ 答案 ] B 　 [ 解析 ] 如图 , 作 EF ∥ AB , ∵ AB ∥ CD , ∴ EF ∥ AB ∥ CD , ∴∠ 2 = ∠ AEF= 35°, ∠ 1 = ∠ FEC. ∵∠ AEC= 90°, ∴∠ 1 = ∠ FEC= 90°-35° = 55°, 故选 B . | 考向精练 | 1 . [2015· 呼和浩特 3 题 ] 如图 16-11, 已知∠ 1 = 70°, 如果 CD ∥ BE , 那么∠ B 的度数为 ( 　　 ) A . 70° B . 100° C . 110° D . 120° 图 16-11 [ 答案 ] C 　 [ 解析 ] 如图 , ∵∠ 1 = 70°, ∴∠ 2 = ∠ 1 = 70°, ∵ CD ∥ BE , ∴∠ B= 180°- ∠ 2 = 180°-70° = 110° . 故选 :C . 2 . [2017· 鄂尔多斯 ] 如图 16-12 是一副三角尺 ABC 与 DEF 拼成的图案 , 若将三角尺 DEF 绕点 M 按顺时针方向旋转 , 则边 DE 与边 AB 第一次平行时 , 旋转角的度数是 ( 　　 ) A . 75° B . 60° C . 45° D . 30° 图 16-12 [ 答案 ] C 　 [ 解析 ] 过 M 作 MH ∥ AB 交 BC 于 H , ∵ AB ⊥ BC , ∴ MH ⊥ BC , ∴ △ BMH 是等腰直角三角形 , ∴∠ BMH= 45°, ∴若将三角尺 DEF 绕点 M 按顺时针方向旋转 , 则边 DE 与边 AB 第一次平行时 , 旋转角的度数是 45°, 故选 C . 3 . 如图 16-13, 从①∠ 1 = ∠ 2, ②∠ C= ∠ D , ③∠ A= ∠ F 三个条件中选出两个作为已知条件 , 另一个作为结论所组成的命题中 , 正确命题的个数为 ( 　　 ) A . 0 B . 1 C . 2 D . 3 图 16-13 [ 答案 ] D 4 . [2019· 河北 ] 下面是投影屏上出示的抢答题 , 需要回答横线上符号代表的内容 . 已知 : 如图 , ∠ BEC= ∠ B + ∠ C. 求证 : AB ∥ CD. 证明 : 延长 BE 交 　 ※ 　 于点 F , 则∠ BEC= 　 ◎ 　 + ∠ C ( 三角形的外角等于与它不相邻两个内角之和 ) .  又∠ BEC= ∠ B + ∠ C , 得∠ B= 　 ▲ 　 ,  故 AB ∥ CD ( 　 @ 　 相等 , 两直线平行 ) .  　 　　　　　　　 则回答正确的是 ( 　　 ) A . ◎ 代表∠ FEC B .@ 代表同位角 C . ▲ 代表∠ EFC D . ※ 代表 AB 图 16-14 [ 答案 ] C 　 [ 解析 ] 从图上看 , 延长 BE 交 CD 于点 F , 所以 ※ 代表 AB 不正确 , 选项 D 不正确 ; 利用 “ 三角形的外角等于与它不相邻两个内角之和 ” 判断∠ BEC= ∠ EFC + ∠ C , 所以 ◎ 代表∠ FEC 不正确 , 选项 A 不正确 ; 利用 “ 等量代换 ” 判断∠ B= ∠ EFC , 所以选项 C 是正确的 ; ∠ B 和∠ EFC 是内错角 , 所以选项 B 不正确 . 因此正确的选项是 C . 5 . [2017· 呼和浩特 12 题 ] 如图 16-15, AB ∥ CD , AE 平分∠ CAB 交 CD 于点 E , 若∠ C= 48°, 则∠ AED 为 　　　　 ° .  图 16-15 114 6 . [2013· 呼和浩特 11 题 ] 如图 16-16, AB ∥ CD , ∠ 1 = 60°, FG 平分∠ EFD , 则∠ 2 = 　　　　 度 .  图 16-16 30