2018年安徽省中考数学试卷

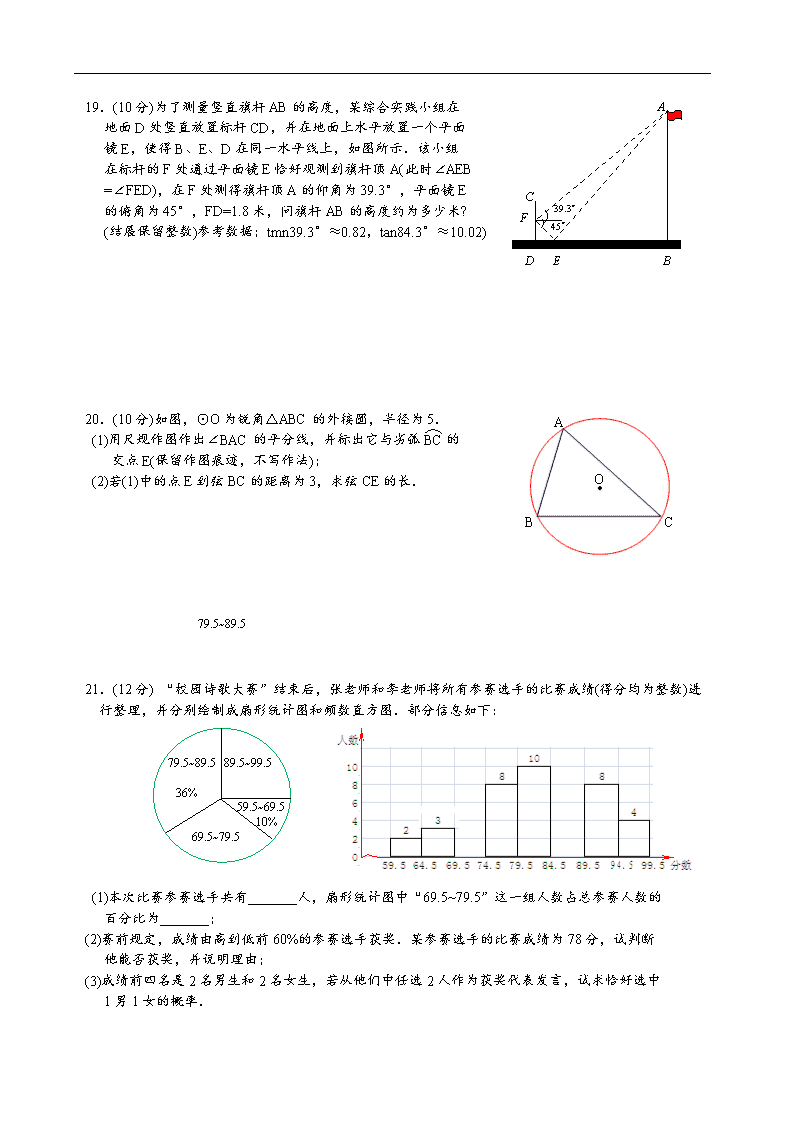
2018年安徽省中考数学试卷

‎2018年安徽省中考数学试题 一、选择题(共40分)‎ ‎1．–8的绝对值是( ) ．‎ A．–8 B．8 C．±8 D．–‎ ‎2．2017年我省粮食总产量为695.2亿斤，其中695.2亿用科学记数法表示为( ) ．‎ A．6.952×106 B．6.952×109 C．6.952×109　　C．D．695.2×108‎ ‎3．下列运算正确的是( ) ．‎ A． (a2)3= a5 B． a4·a2= a6 C． a6÷a2=a2 D．(ab)5=a3b2‎ ‎4．一个由圆柱和圆锥组成的几何体如图水平放置，其主(正)视图为( ) ．‎ D C B A ‎5．下列分解因式正确的是( ) ．‎ A．–x2+4x=–x(x+4) B． x2+xy+x=x(x+y)‎ C． x(x–y)+y(y–x)=(x–y)2 D．x2–4x+4=(x+2)(x–2)‎ ‎6．据省统计局发布：2017年我省有效发明专利数比2016年增长22.1%．假定2018年的年增长率保持不变，2016年和2018年我省有效发明专利分别为a万件和b万件，则( ) ．‎ A．b=(1+22.1%×2)a B．b=(1+22.1%)2a C．b=(1+22.1%)×2a D．b=22.1%×2a ‎7．若关于x的一元二次方程x(x+1)+ax=0有两个相等的实数根，则实数a的值为( ) ．‎ A．–1 B．1 C．–2或2 D．–3或1‎ ‎8．为考察两名实习工人的工作情况，质检部将他们工作第一周每天生产合格产品的个数整理成甲、乙两组数据，如下表：‎ 甲 ‎2‎ ‎6‎ ‎7‎ ‎7‎ ‎8‎ 乙 ‎2‎ ‎3‎ ‎4‎ ‎8‎ ‎8‎ 关于以上数据，说法正确的是( ) ．‎ A．甲、乙的众数相同 B．甲、乙的中位数相 C．甲的平均数小于乙的平均数 D．甲的方差小于乙的方差 ‎9．□ABCD中、E，F是对角线BD上不同的两点，下列条件中，不能得出四边形AECF一定为平行四边形的是( ) ．‎ A． BE= DF B．AE=CF　 C．AF∥CE　 D．∠BAE=∠DCF y O–‎ x ‎1 2‎ y O–‎ x ‎1 2‎ y O–‎ x ‎1 2‎ y O–‎ x ‎1 2‎ A．‎ B．‎ C．‎ D．‎ A–‎ B–‎ M(C) N D–‎ l1–‎ l2–‎ l ‎10．如图，直线l1、l2都与直线l垂直，垂足分别为M、N，MN=1．正方形ABCD的边长为，对角线AC在直线l上，且点C位于点M处．将正方形ABCD沿l向右平移，直到点A与点N重合为止．记点C平移的距离为x，正方形ABCD的边位l1、l2之间部分的长度和为y，则y关于x的函数图象大致为( ) ．‎ 二、填空题(共20分)‎ ‎11．不等式>1的解集是_______．‎ ‎12．如图，菱形ABOC的边AB、AC分别与⊙O相切于点D、E．若点D是AB的中点，则∠DOE=_______．‎ ‎13．如图，正比例函数y=kx与反比例函数y=的图象有一个交点A(2，m)，AB⊥x轴于点B．平移直线y=kx，使其经过点B，得到直线l，则直线l对应的函数表达式_______．‎ ‎14．矩形ABCD中，AB=6，BC=8．点P在矩形ABCD的内部，点E在边BC上，满足△PBE∽△DBC．若△APD是等腰三角形，则PE的长为_______．‎ 三、解答题(共90分)‎ ‎15．(8分)计算5°–(–2)+×‎ ‎16．(8分)《孙子算经》中有这样一道题，原文如下：‎ 今有百良鹿入城，家取一鹿，不尽，又三家共一鹿，适尽．问：域中家几何?大意是：今有100头鹿进城，每家取一头鹿，没有取完，剩下的鹿母3家共取一头，恰好取完．问：城中有多少户人家? 请解答上述问题 ‎17．(8分)如图，在由边长为1个单位长度的小正方形组成的10×10‎ 网格中，已知点O、A、B均为网格线的交点．‎ ‎(1)在给定的网格中，以点O为位似中心，将线段AB放大为原来的 ‎ 2倍，得到线段A1B1（点A、B的对应点分别为A1、B1）．画出 线段A1B1；‎ ‎(2)将线段A1B1绕点B1逆时针旋转90°得到线段A2B1．画出线段 A2B1；‎ ‎ (3)以A、A1、B1、A2为顶点的四边形AA1B1A2的面积是____个单位．‎ ‎18．(8分)观察以下等式：‎ 第1个等式：++×=1‎ 第2个等式：++×=1‎ 第3个等式：++×=1‎ 第4个等式：++×=1‎ 第5个等式：++×=1‎ ‎……‎ 按照以上规律，解决下列问题：‎ ‎(1)写出第6个等式：__________________；‎ ‎(2)写出你猜想的第n个等式：__________________ (用含n的等式表示)，并证明．‎ C A F D E B ‎39.3°‎ ‎45°‎ ‎19．(10分)为了测量竖直旗杆AB的高度，某综合实践小组在 地面D处竖直放置标杆CD，并在地面上水平放置一个平面 镜E，使得B、E、D在同一水平线上，如图所示．该小组 在标杆的F处通过平面镜E恰好观测到旗杆顶A(此时∠AEB ‎=∠FED)，在F处测得旗杆顶A的仰角为39.3°，平面镜E 的俯角为45°，FD=1.8米，问旗杆AB的高度约为多少米?‎ ‎(结展保留整数)参考数据；tmn39.3°≈0.82，tan84.3°≈10.02)‎ A B C O ‎20．(10分)如图，⊙O为锐角△ABC的外接圆，半径为5．‎ ‎ (1)用尺规作图作出∠BAC的平分线，并标出它与劣弧BC的 交点E(保留作图痕迹，不写作法)；‎ ‎(2)若(1)中的点E到弦BC的距离为3，求弦CE的长．‎ ‎79.5~89.5‎ ‎21．(12分) “校园诗歌大赛”结束后，张老师和李老师将所有参赛选手的比赛成绩(得分均为整数)进 行整理，并分别绘制成扇形统计图和频数直方图．部分信息如下：‎ ‎79.5~89.5‎ ‎36%‎ ‎89.5~99.5‎ ‎59.5~69.5‎ ‎69.5~79.5‎ ‎10%‎ ‎ (1)本次比赛参赛选手共有_______人，扇形统计图中“69.5~79.5”这一组人数占总参赛人数的 百分比为_______；‎ ‎(2)赛前规定，成绩由高到低前60%的参赛选手获奖．某参赛选手的比赛成绩为78分，试判断 他能否获奖，并说明理由；‎ ‎(3)成绩前四名是2名男生和2名女生，若从他们中任选2人作为获奖代表发言，试求恰好选中 ‎1男1女的概率．‎ ‎22．(12分)小明大学毕业回家乡创业．第一期培植盆景与花弃各50盆．售后统计，盆景的平均每盆利润是160元，花卉的平均每盆利润是19元．调研发现：‎ ‎①盆景每增加1盆，盆景的平均每盆利润减少2元；每减少1盆，盆景的平均每盆利润增加2元；‎ ‎②花卉的平均每盆利润始终不变．‎ 小明计划第二期培植盆景与花卉共100盆，设培植的盆景比第一期增加x盆，第二期盆景与花卉售完后的利润分别为W1，W2(单位：元) ．‎ ‎(1)用含x的代数式分别表示W1，W2；‎ ‎(2)当x取何值时，第二期培植的盆景与花卉售完后获得的总利润W最大，最大总利润是多少?‎ ‎23．(14分)如圈1，Rt△ABC中，∠ACB=90°，点D为边AC上一点，DE⊥AB于点E，点M为BD中点，CM的延长线交AB于点F．‎ ‎（1）求证：CM=EM；‎ ‎（2）若∠BMC=50°∠EMF的大小；‎ A B C D M E F N 图2‎ A B C D E F M 图1‎ ‎（3）如图2，若△DAE≌△CEM，点N为CM的中点求证：AN∥EM