数学冀教版九年级上册教案28-2过三点的圆

数学冀教版九年级上册教案28-2过三点的圆

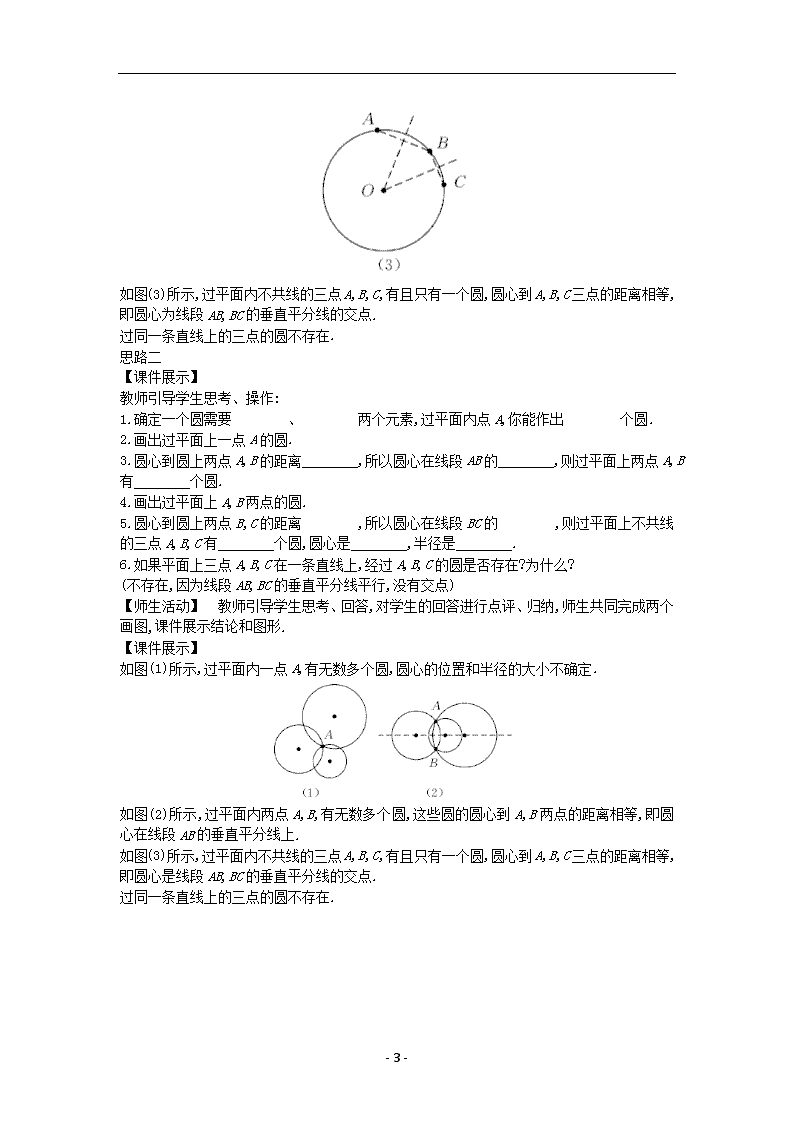
- 1 - 28.2 过三点的圆 教学目标 【知识与能力】 1.了解三角形的外接圆、三角形的外心、圆的内接三角形的概念. 2.理解“不在同一条直线上的三点确定一个圆”. 3.能熟练掌握应用尺规过不在同一条直线上的三点作圆的方法. 【过程与方法】 1.通过独立思考、动手操作、合作交流等数学活动,不断积累数学活动的经验,提高学生动手 操作的能力,体会转化、数形结合思想在数学中的应用. 2.通过学生自己动手作图,在动手参与的过程中探索、发现科学知识,进一步提高学生动手操 作的积极性,提高学生应用数学知识解决实际问题的能力. 【情感态度价值观】 1.通过探索知识的过程激发学生观察、探究、发现数学问题和解决数学问题的兴趣和欲望. 2.通过小组合作交流,学会与他人合作,并能与他人交流思维的过程和结果. 3.增强学生的数学应用意识,提高学生学习数学的兴趣,培养学生永无止境的科学探索精神. 教学重难点 【教学重点】 “过不在同一条直线上的三点作圆”的方法. 【教学难点】 如何确定圆的思维过程. 课前准备 多媒体课件 教学过程 一、新课导入： 导入一: 复习提问: 1.根据圆的定义,确定圆的两个基本要素是什么? 2.如何用尺规作图作线段的垂直平分线? 3.线段垂直平分线有什么性质? 4.三角形三边的垂直平分线的交点有几个?交点与三角形三个顶点之间在距离上有什么关 系? 导入二: 一位考古学家在长沙马王堆汉墓挖掘时,发现一圆形瓷器碎片,你能帮助这位考古学家画出 这个碎片所在的整个圆吗? - 2 - [过渡语] 要画出圆就要找到圆心和半径,怎样找到圆心和半径,我们学习了这节课后 就会找到答案. [设计意图] 通过提问,既复习了前面的知识,又使学生进入了状态,为本节课的学习做好铺 垫.由生活实例导入新课,激发学生的求知欲望,让每个学生都迅速进入积极思维的状态. 二、新知构建： [过渡语] 两点能够确定一条直线.那么,两个点能确定一个圆吗?三个点呢?让我们一 起探究这些问题! 共同探究 不在同一条直线上的三点确定一个圆 思路一 【课件展示】 动手操作,并思考回答: 1.作圆,使该圆经过已知点 A,你能作出几个这样的圆? (圆心和半径的位置不定,可以作出无数个圆) 2.平面上有两点 A,B,过点 A,B 的圆有多少个?这些圆的圆心到点 A,B 的距离具有怎样的关系? 圆心是否在线段 AB 的垂直平分线上? (过两点 A,B 的圆有无数个,这些圆的圆心到点 A,B 的距离相等,它们的圆心在线段 AB 的垂直 平分线上) 【师生活动】 学生独立思考、动手画图,小组合作交流,针对 2 教师引导:圆上的点到圆心 的距离相等,确定圆心的位置时,使它到点 A,B 的距离相等,圆心在线段 AB 的垂直平分线上. 学生黑板上作图,教师进行点评. 3.平面上三点 A,B,C 不在一条直线上.过点 A,B,C 的圆是否存在?如果存在,这样的圆有多少 个?你能确定经过 A,B,C 三点的圆的圆心及半径吗? (存在,只有一个,分别作线段 AB,BC 的垂直平分线,两条垂直平分线的交点就是圆心,圆心到 其中一点的距离就是半径) 4.如果平面上三点 A,B,C 在一条直线上,经过 A,B,C 的圆是否存在?为什么? (不存在,因为线段 AB,BC 的垂直平分线平行,没有交点) 【师生活动】 学生独立思考后小组合作交流,教师巡视中帮助有困难的学生,对有困难的学 生引导分析,所求的圆要经过 A,B,C 三点,所以圆心到这三点的距离相等,因此这个点要在线 段 AB 的垂直平分线上,又要在线段 BC 的垂直平分线上.教师对学生的回答进行点评纠正,师 生共同归纳结论,然后课件展示. 【课件展示】 如图(1)所示,过平面内一点 A,有无数多个圆,圆心的位置和半径的大小不确定. 如图(2)所示,过平面内两点 A,B,有无数多个圆,这些圆的圆心到 A,B 两点的距离相等,即圆 心在线段 AB 的垂直平分线上. - 3 - 如图(3)所示,过平面内不共线的三点 A,B,C,有且只有一个圆,圆心到 A,B,C 三点的距离相等, 即圆心为线段 AB,BC 的垂直平分线的交点. 过同一条直线上的三点的圆不存在. 思路二 【课件展示】 教师引导学生思考、操作: 1.确定一个圆需要 、 两个元素,过平面内点 A,你能作出 个圆. 2.画出过平面上一点 A 的圆. 3.圆心到圆上两点 A,B 的距离 ,所以圆心在线段 AB 的 ,则过平面上两点 A,B 有 个圆. 4.画出过平面上 A,B 两点的圆. 5.圆心到圆上两点 B,C 的距离 ,所以圆心在线段 BC 的 ,则过平面上不共线 的三点 A,B,C 有 个圆,圆心是 ,半径是 . 6.如果平面上三点 A,B,C 在一条直线上,经过 A,B,C 的圆是否存在?为什么? (不存在,因为线段 AB,BC 的垂直平分线平行,没有交点) 【师生活动】 教师引导学生思考、回答,对学生的回答进行点评、归纳,师生共同完成两个 画图,课件展示结论和图形. 【课件展示】 如图(1)所示,过平面内一点 A,有无数多个圆,圆心的位置和半径的大小不确定. 如图(2)所示,过平面内两点 A,B,有无数多个圆,这些圆的圆心到 A,B 两点的距离相等,即圆 心在线段 AB 的垂直平分线上. 如图(3)所示,过平面内不共线的三点 A,B,C,有且只有一个圆,圆心到 A,B,C 三点的距离相等, 即圆心是线段 AB,BC 的垂直平分线的交点. 过同一条直线上的三点的圆不存在. - 4 - [设计意图] 通过动手操作、观察思考、合作交流、归纳结论,体会数形结合思想在数学中 的应用,培养学生的数学思维能力和归纳总结能力,同时掌握把实际问题抽象转化为数学问 题的重要思路. 做一做: 如图所示,过不在同一条直线上的三点 A,B,C 画圆. 【师生活动】 教师给学生足够的时间动手操作,然后小组交流答案,小组代表板书过程(或 教师课件动画展示画图过程),并做出点评. 【课件展示】 作法:如图所示. 1.分别连接 AB,BC; 2.分别作出线段 AB,BC 的垂直平分线 l1 和 l2,设它们的交点为 O,则 OA=OB=OC; 3.以点 O 为圆心,OA(或 OB,OC)为半径作圆,则☉O 即为所作的圆. 结论:不在同一条直线上的三点确定一个圆. [设计意图] 通过动手操作,引导学生进一步认识“过不在同一条直线上的三点只能画出一 个圆”这一事实,进一步体验数学活动的探索与创造,感受数学的严谨性. 例题讲解 - 5 - (教材 151 页例)用尺规作过三角形三个顶点的圆. 已知:如图所示,△ABC. 求作:☉O,使它过三点 A,B,C. 【师生活动】 学生独立完成作图过程,学生展示回答作图过程,并完成板书,教师课件展示 作法,规范学生的几何语言,并归纳三角形的外接圆的概念. 【课件展示】 作法:如图所示. (1)分别作线段 AB 和 BC 的垂直平分线 l1 和 l2.设 l1 与 l2 相交于点 O. (2)以点 O 为圆心,OA 为半径画圆. ☉O 即为所求. 我们把经过三角形三个顶点的圆,叫做三角形的外接圆,外接圆的圆心叫做三角形的外心. 【思考】 1.三角形的外心到三角形的三个顶点的距离有什么关系? 2.钝角三角形、直角三角形、锐角三角形的外心在什么位置? 【师生活动】 学生独立思考后,小组合作交流,学生回答问题,教师点评归纳. [设计意图] 通过动手操作、思考交流,进一步体验数学活动的探索与创造,感受数学的严谨 性,让学生经历知识的形成过程,提高学生分析问题、解决问题的能力和数学思维. - 6 - (节前导入情境)一位考古学家在长沙马王堆汉墓挖掘时,发现一圆形瓷器碎片,你能 帮助这位考古学家画出这个碎片所在的整个圆吗? 【师生活动】 学生独立思考后小组合作交流,共同完成确定圆心的过程,教师巡视中帮助有 困难的学生,对学生的展示点评,并归纳已知一段弧,作所在圆的圆心的方法. 结论: 在残缺的圆上(或弧上)任意选取三点,确定过这三点的圆心就是所在圆的圆心. [设计意图] 学生通过独立思考、合作交流完成节前导入生活情境,做到整节课首尾呼应, 让学生体会数学在实际生活中的应用,巩固作三角形的外接圆的方法,同时培养学生的合作 精神以及数学的应用意识. [知识拓展] 1.经过同一条直线上的三个点不能作圆,要注意“过三点的圆”中的“三点”不在同一直线 上,故“过三点有且只有一个圆”这种说法是错误的. 2.“确定”一词是指不仅能作出一个圆,而且只能作出一个圆,即“有且只有”的意思. 3.任意一个三角形都有且只有一个外接圆. 4.三角形的外心不仅是三角形外接圆的圆心,它还是三角形三条边的垂直平分线的交点,它 到三角形各个顶点的距离相等. 5.锐角三角形的外心在三角形的内部;直角三角形的外心为直角三角形斜边的中点;钝角三 角形的外心在三角形的外部. 三、课堂小结： 1.过平面内一点有无数多个圆. 2.过平面内两点有无数多个圆,圆心在线段的垂直平分线上. 3.作三角形的外接圆. 4.不在同一条直线上的三点确定一个圆.