- 2021-11-10 发布 |
- 37.5 KB |
- 28页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019湖北省武汉市中考数学试卷
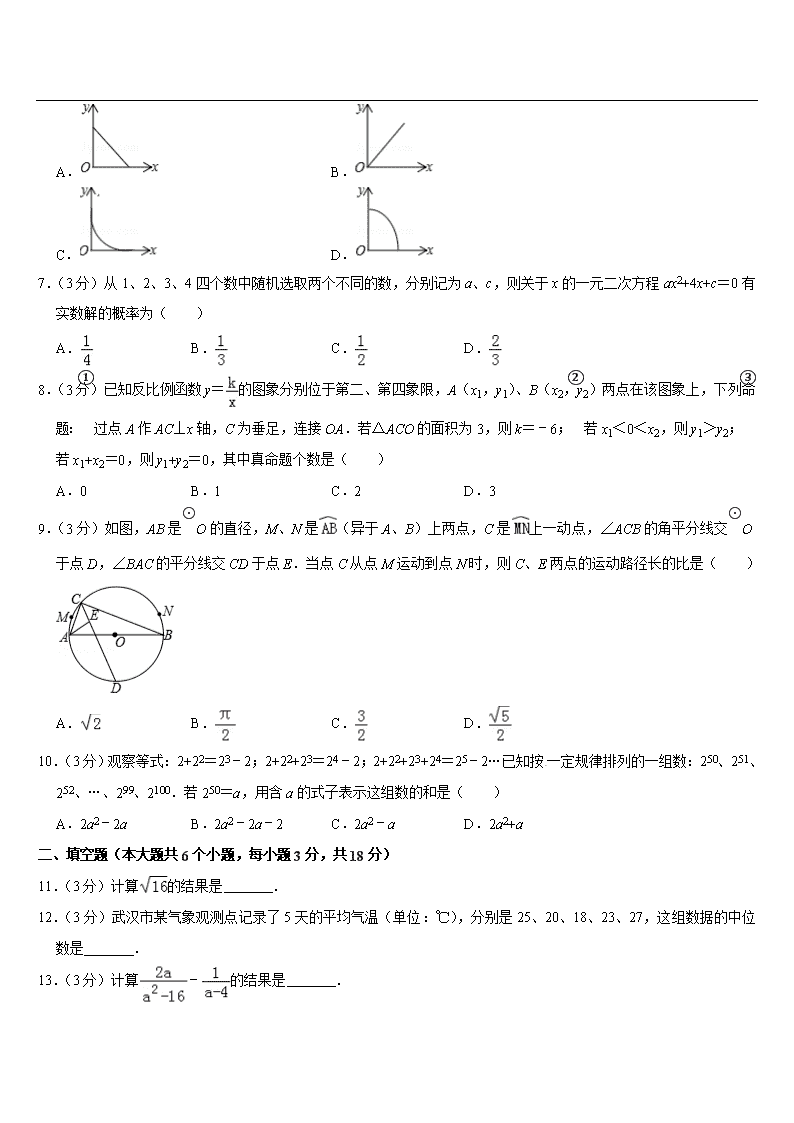
2019年湖北省武汉市中考数学试卷 一、选择题(共10小题,每小题3分,共30分) 1.(3分)实数2019的相反数是( ) A.2019 B.﹣2019 C. D. 2.(3分)式子在实数范围内有意义,则x的取值范围是( ) A.x>0 B.x≥﹣1 C.x≥1 D.x≤1 3.(3分)不透明的袋子中只有4个黑球和2个白球,这些球除颜色外无其他差别,随机从袋子中一次摸出3个球,下列事件是不可能事件的是( ) A.3个球都是黑球 B.3个球都是白球 C.三个球中有黑球 D.3个球中有白球 4.(3分)现实世界中,对称现象无处不在,中国的方块字中有些也具有对称性,下列美术字是轴对称图形的是( ) A. B. C. D. 5.(3分)如图是由5个相同的小正方体组成的几何体,该几何体的左视图是( ) A. B. C. D. 6.(3分)“漏壶”是一种古代计时器,在它内部盛一定量的水,不考虑水量变化对压力的影响,水从壶底小孔均匀漏出,壶内壁有刻度.人们根据壶中水面的位置计算时间,用t表示漏水时间,y表示壶底到水面的高度,下列图象适合表示y与x的对应关系的是( ) A. B. C. D. 7.(3分)从1、2、3、4四个数中随机选取两个不同的数,分别记为a、c,则关于x的一元二次方程ax2+4x+c=0有实数解的概率为( ) A. B. C. D. 8.(3分)已知反比例函数y=的图象分别位于第二、第四象限,A(x1,y1)、B(x2,y2)两点在该图象上,下列命题:①过点A作AC⊥x轴,C为垂足,连接OA.若△ACO的面积为3,则k=﹣6;②若x1<0<x2,则y1>y2;③若x1+x2=0,则y1+y2=0,其中真命题个数是( ) A.0 B.1 C.2 D.3 9.(3分)如图,AB是⊙O的直径,M、N是(异于A、B)上两点,C是上一动点,∠ACB的角平分线交⊙O于点D,∠BAC的平分线交CD于点E.当点C从点M运动到点N时,则C、E两点的运动路径长的比是( ) A. B. C. D. 10.(3分)观察等式:2+22=23﹣2;2+22+23=24﹣2;2+22+23+24=25﹣2…已知按一定规律排列的一组数:250、251、252、…、299、2100.若250=a,用含a的式子表示这组数的和是( ) A.2a2﹣2a B.2a2﹣2a﹣2 C.2a2﹣a D.2a2+a 二、填空题(本大题共6个小题,每小题3分,共18分) 11.(3分)计算的结果是 . 12.(3分)武汉市某气象观测点记录了5天的平均气温(单位:℃),分别是25、20、18、23、27,这组数据的中位数是 . 13.(3分)计算﹣的结果是 . 14.(3分)如图,在▱ABCD中,E、F是对角线AC上两点,AE=EF=CD,∠ADF=90°,∠BCD=63°,则∠ADE的大小为 . 15.(3分)抛物线y=ax2+bx+c经过点A(﹣3,0)、B(4,0)两点,则关于x的一元二次方程a(x﹣1)2+c=b﹣bx的解是 . 16.(3分)问题背景:如图1,将△ABC绕点A逆时针旋转60°得到△ADE,DE与BC交于点P,可推出结论:PA+PC=PE. 问题解决:如图2,在△MNG中,MN=6,∠M=75°,MG=.点O是△MNG内一点,则点O到△MNG三个顶点的距离和的最小值是 .[来源:学§科§网Z§X§X§K] 三、解答题(共8题,共72分) 17.(8分)计算:(2x2)3﹣x2•x4. 18.(8分)如图,点A、B、C、D在一条直线上,CE与BF交于点G,∠A=∠1,CE∥DF,求证:∠E=∠F. 19.(8分)为弘扬中华传统文化,某校开展“双剧进课堂”的活动,该校童威随机抽取部分学生,按四个类别:A表示“很喜欢”,B表示“喜欢”,C表示“一般”,D表示“不喜欢”,调查他们对汉剧的喜爱情况,将结果绘制成如下两幅不完整的统计图,根据图中提供的信息,解决下列问题: (1)这次共抽取 名学生进行统计调查,扇形统计图中,D类所对应的扇形圆心角的大小为 ; (2)将条形统计图补充完整; (3)该校共有1500名学生,估计该校表示“喜欢”的B类的学生大约有多少人? 20.(8分)如图是由边长为1的小正方形构成的网格,每个小正方形的顶点叫做格点.四边形ABCD的顶点在格点上,点E是边DC与网格线的交点.请选择适当的格点,用无刻度的直尺在网格中完成下列画图,保留连线的痕迹,不要求说明理由. (1)如图1,过点A画线段AF,使AF∥DC,且AF=DC. (2)如图1,在边AB上画一点G,使∠AGD=∠BGC. (3)如图2,过点E画线段EM,使EM∥AB,且EM=AB. 21.(8分)已知AB是⊙O的直径,AM和BN是⊙O的两条切线,DC与⊙O相切于点E,分别交AM、BN于D、C两点. (1)如图1,求证:AB2=4AD•BC; (2)如图2,连接OE并延长交AM于点F,连接CF.若∠ADE=2∠OFC,AD=1,求图中阴影部分的面积. 22.(10分)某商店销售一种商品,童威经市场调查发现:该商品的周销售量y(件)是售价x(元/件)的一次函数,其售价、周销售量、周销售利润w(元)的三组对应值如表: 售价x(元/件)[来源:学,科,网] 50 60 80 周销售量y(件) 100 80 40 周销售利润w(元) 1000 1600 1600 注:周销售利润=周销售量×(售价﹣进价) (1)①求y关于x的函数解析式(不要求写出自变量的取值范围); ②该商品进价是 元/件;当售价是 元/件时,周销售利润最大,最大利润是 元. (2)由于某种原因,该商品进价提高了m元/件(m>0),物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求m的值. 23.(10分)在△ABC中,∠ABC=90°,=n,M是BC上一点,连接AM. (1)如图1,若n=1,N是AB延长线上一点,CN与AM垂直,求证:BM=BN. (2)过点B作BP⊥AM,P为垂足,连接CP并延长交AB于点Q. ①如图2,若n=1,求证:=. ②如图3,若M是BC的中点,直接写出tan∠BPQ的值.(用含n的式子表示) 24.(12分)已知抛物线C1:y=(x﹣1)2﹣4和C2:y=x2 (1)如何将抛物线C1平移得到抛物线C2? (2)如图1,抛物线C1与x轴正半轴交于点A,直线y=﹣x+b经过点A,交抛物线C1于另一点B.请你在线段AB上取点P,过点P作直线PQ∥y轴交抛物线C1于点Q,连接AQ. ①若AP=AQ,求点P的横坐标; ②若PA=PQ,直接写出点P的横坐标. (3)如图2,△MNE的顶点M、N在抛物线C2上,点M在点N右边,两条直线ME、NE与抛物线C2均有唯一公共点,ME、NE均与y轴不平行.若△MNE的面积为2,设M、N两点的横坐标分别为m、n,求m与n的数量关系. [来源:Z#xx#k.Com] 2019年湖北省武汉市中考数学试卷 参考答案与试题解析 一、选择题(共10小题,每小题3分,共30分) 1.(3分)实数2019的相反数是( ) A.2019 B.﹣2019 C. D. 【分析】直接利用相反数的定义进而得出答案. 【解答】解:实数2019的相反数是:﹣2009. 故选:B. 【点评】此题主要考查了相反数,正确把握相反数的定义是解题关键. 2.(3分)式子在实数范围内有意义,则x的取值范围是( ) A.x>0 B.x≥﹣1 C.x≥1 D.x≤1 【分析】根据被开方数是非负数,可得答案. 【解答】解:由题意,得 x﹣1≥0, 解得x≥1, 故选:C. 【点评】本题考查了二次根式有意义的条件,利用被开方数是非负数得出不等式组是解题关键. 3.(3分)不透明的袋子中只有4个黑球和2个白球,这些球除颜色外无其他差别,随机从袋子中一次摸出3个球,下列事件是不可能事件的是( ) A.3个球都是黑球 B.3个球都是白球 C.三个球中有黑球 D.3个球中有白球 【分析】根据事件发生的可能性大小判断相应事件的类型. 【解答】解:A、3个球都是黑球是随机事件; B、3个球都是白球是不可能事件; C、三个球中有黑球是必然事件; D、3个球中有白球是随机事件; 故选:B. 【点评】 本题考查的是必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件. 4.(3分)现实世界中,对称现象无处不在,中国的方块字中有些也具有对称性,下列美术字是轴对称图形的是( ) A. B. C. D. 【分析】利用轴对称图形定义判断即可. 【解答】解:四个汉字中,可以看作轴对称图形的是, 故选:D. 【点评】此题考查了轴对称图形,熟练掌握轴对称图形的定义是解本题的关键. 5.(3分)如图是由5个相同的小正方体组成的几何体,该几何体的左视图是( ) A. B. C. D. 【分析】找到从左面看所得到的图形即可,注意所有的看到的棱都应表现在主视图中. 【解答】解:从左面看易得下面一层有2个正方形,上面一层左边有1个正方形,如图所示:. 故选:A. 【点评】本题考查了三视图的知识,左视图是从物体的左面看得到的视图. 6.(3分)“漏壶”是一种古代计时器,在它内部盛一定量的水,不考虑水量变化对压力的影响,水从壶底小孔均匀漏出,壶内壁有刻度.人们根据壶中水面的位置计算时间,用t表示漏水时间,y表示壶底到水面的高度,下列图象适合表示y与x的对应关系的是( ) A. B. C. D. 【分析】根据题意,可知y随的增大而减小,符合一次函数图象,从而可以解答本题. 【解答】解:∵不考虑水量变化对压力的影响,水从壶底小孔均匀漏出,t表示漏水时间,y表示壶底到水面的高度, ∴y随t的增大而减小,符合一次函数图象, 故选:A. 【点评】本题考查函数图象,解答本题的关键是明确题意,利用数形结合的思想解答. 7.(3分)从1、2、3、4四个数中随机选取两个不同的数,分别记为a、c,则关于x的一元二次方程ax2+4x+c=0有实数解的概率为( ) A. B. C. D. 【分析】首先画出树状图即可求得所有等可能的结果与使ac≤4的情况,然后利用概率公式求解即可求得答案. 【解答】解:画树状图得: 由树形图可知:一共有12种等可能的结果,其中使ac≤4的有6种结果, ∴关于x的一元二次方程ax2+4x+c=0有实数解的概率为, 故选:C. 【点评】本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比. 8.(3分)已知反比例函数y=的图象分别位于第二、第四象限,A(x1,y1)、B(x2,y2)两点在该图象上,下列命题:①过点A作AC⊥x轴,C为垂足,连接OA.若△ACO的面积为3,则k=﹣6;②若x1<0<x2,则y1>y2;③若x1+x2=0,则y1+y2=0,其中真命题个数是( ) A.0 B.1 C.2 D.3 【分析】利用反比例函数的比例系数的几何意义、反比例函数的增减性、对称性分别回答即可. 【解答】解:过点A作AC⊥x轴,C为垂足,连接OA. ∵△ACO的面积为3, ∴|k|=6, ∵反比例函数y=的图象分别位于第二、第四象限, ∴k<0, ∴k=﹣6,正确,是真命题; ②∵反比例函数y=的图象分别位于第二、第四象限, ∴在所在的每一个象限y随着x的增大而增大, 若x1<0<x2,则y1>0>y2,正确,是真命题; ③当A、B两点关于原点对称时,x1+x2=0,则y1+y2=0,正确,是真命题, 真命题有3个, 故选:D. 【点评】本题考查了反比例函数的性质及命题与定理的知识,解题的关键是了解反比例函数的比例系数的几何意义等知识,难度不大. 9.(3分)如图,AB是⊙O的直径,M、N是(异于A、B)上两点,C是上一动点,∠ACB的角平分线交⊙O于点D,∠BAC的平分线交CD于点E.当点C从点M运动到点N时,则C、E两点的运动路径长的比是( ) A. B. C. D. 【分析】如图,连接EB.设OA=r.易知点E在以D为圆心DA为半径的圆上,运动轨迹是,点C的运动轨迹是,由题意∠MON=2∠GDF,设∠GDF=α,则∠MON=2α,利用弧长公式计算即可解决问题. 【解答】解:如图,连接EB.设OA=r. ∵AB是直径, ∴∠ACB=90°, ∵E是△ACB的内心, ∴∠AEB=135°, ∵∠ACD=∠BCD, ∴=, ∴AD=DB=r, ∴∠ADB=90°, 易知点E在以D为圆心DA为半径的圆上,运动轨迹是,点C的运动轨迹是, ∵∠MON=2∠GDF,设∠GDF=α,则∠MON=2α ∴==. 故选:A. 【点评】本题考查弧长公式,圆周角定理,三角形的内心等知识,解题的关键是理解题意,正确寻找点的运动轨迹,属于中考选择题中的压轴题. 10.(3分)观察等式:2+22=23﹣2;2+22+23=24﹣2;2+22+23+24=25﹣2…已知按一定规律排列的一组数:250、251、252、…、299、2100.若250=a,用含a的式子表示这组数的和是( ) A.2a2﹣2a B.2a2﹣2a﹣2 C.2a2﹣a D.2a2+a 【分析】由等式:2+22=23﹣2;2+22+23=24﹣2;2+22+23+24=25﹣2,得出规律:2+22+23+…+2n=2n+1﹣2,那么250+251+252+…+299+2100=(2+22+23+…+2100)﹣(2+22+23+…+249),将规律代入计算即可. 【解答】解:∵2+22=23﹣2; 2+22+23=24﹣2; 2+22+23+24=25﹣2; … ∴2+22+23+…+2n=2n+1﹣2, ∴250+251+252+…+299+2100 =(2+22+23+…+2100)﹣(2+22+23+…+249) =(2101﹣2)﹣(250﹣2) =2101﹣250, ∵250=a, ∴2101=(250)2•2=2a2, ∴原式=2a2﹣a. 故选:C. 【点评】本题是一道找规律的题目,要求学生通过观察,分析、归纳发现其中的规律,并应用发现的规律解决问题.解决本题的难点在于得出规律:2+22+23+…+2n=2n+1﹣2. 二、填空题(本大题共6个小题,每小题3分,共18分) 11.(3分)计算的结果是 4 . 【分析】根据二次根式的性质求出即可. 【解答】解:=4, 故答案为:4. 【点评】本题考查了二次根式的性质和化简,能熟练地运用二次根式的性质进行化简是解此题的关键. 12.(3分)武汉市某气象观测点记录了5天的平均气温(单位:℃),分别是25、20、18、23、27,这组数据的中位数是 23℃ . 【分析】根据中位数的概念求解可得. 【解答】解:将数据重新排列为18、20、23、25、27, 所以这组数据的中位数为23℃, 故答案为:23℃. 【点评】 此题考查了中位数,将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数. 13.(3分)计算﹣的结果是 . 【分析】异分母分式相加减,先通分变为同分母分式,然后再加减. 【解答】解:原式= = = =. 故答案为: 【点评】此题考查了分式的加减运算,分式的加减运算关键是通分,通分的关键是找最简公分母. 14.(3分)如图,在▱ABCD中,E、F是对角线AC上两点,AE=EF=CD,∠ADF=90°,∠BCD=63°,则∠ADE的大小为 21° . 【分析】设∠ADE=x,由等腰三角形的性质和直角三角形得出∠DAE=∠ADE=x,DE=AF=AE=EF,得出DE=CD,证出∠DCE=∠DEC=2x,由平行四边形的性质得出∠DCE=∠BCD﹣∠BCA=63°﹣x,得出方程,解方程即可. 【解答】解:设∠ADE=x, ∵AE=EF,∠ADF=90°, ∴∠DAE=∠ADE=x,DE=AF=AE=EF, ∵AE=EF=CD, ∴DE=CD, ∴∠DCE=∠DEC=2x, ∵四边形ABCD是平行四边形, ∴AD∥BC, ∴∠DAE=∠BCA=x,[来源:学科网ZXXK] ∴∠DCE=∠BCD﹣∠BCA=63°﹣x, ∴2x=63°﹣x, 解得:x=21°, 即∠ADE=21°; 故答案为:21°. 【点评】本题考查了平行四边形的性质、直角三角形的性质、等腰三角形的性质等知识;根据角的关系得出方程是解题的关键. 15.(3分)抛物线y=ax2+bx+c经过点A(﹣3,0)、B(4,0)两点,则关于x的一元二次方程a(x﹣1)2+c=b﹣bx的解是 x1=﹣2,x2=5 . 【分析】由于抛物线y=ax2+bx+c沿x轴向右平移1个单位得到y=a(x﹣1)2+b(x﹣1)+c,从而得到抛物线y=a(x﹣1)2+b(x﹣1)+c与x轴的两交点坐标为(﹣2,0),(5,0),然后根据抛物线与x轴的交点问题得到一元二方程a(x﹣1)2+b(x﹣1)+c=0的解. 【解答】解:关于x的一元二次方程a(x﹣1)2+c=b﹣bx变形为a(x﹣1)2+b(x﹣1)+c=0, 把抛物线y=ax2+bx+c沿x轴向右平移1个单位得到y=a(x﹣1)2+b(x﹣1)+c, 因为抛物线y=ax2+bx+c经过点A(﹣3,0)、B(4,0), 所以抛物线y=a(x﹣1)2+b(x﹣1)+c与x轴的两交点坐标为(﹣2,0),(5,0), 所以一元二方程a(x﹣1)2+b(x﹣1)+c=0的解为x1=﹣2,x2=5. 故答案为x1=﹣2,x2=5. 【点评】本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.也考查了二次函数的性质. 16.(3分)问题背景:如图1,将△ABC绕点A逆时针旋转60°得到△ADE,DE与BC交于点P,可推出结论:PA+PC=PE. 问题解决:如图2,在△MNG中,MN=6,∠M=75°,MG=.点O是△MNG内一点,则点O到△MNG三个顶点的距离和的最小值是 2 . 【分析】(1)在BC上截取BG=PD,通过三角形求得证得AG=AP,得出△AGP是等边三角形,得出∠AGC=60°=∠APG,即可求得∠APE=60°,连接EC,延长BC到F,使CF=PA,连接EF,证得△ACE是等边三角形,得出 AE=EC=AC,然后通过证得△APE≌△ECF(SAS),得出PE=PF,即可证得结论; (2)以MG为边作等边三角形△MGD,以OM为边作等边△OME.连接ND,可证△GMO≌△DME,可得GO=DE,则MO+NO+GO=NO+OE+DE,即当D、E、O、N四点共线时,MO+NO+GO值最小,最小值为ND的长度,根据勾股定理先求得MF、DF,然后求ND的长度,即可求MO+NO+GO的最小值. 【解答】(1)证明:如图1,在BC上截取BG=PD, 在△ABG和△ADP中 , ∴△ABG≌△ADP(SAS), ∴AG=AP,∠BAG=∠DAP, ∵∠GAP=∠BAD=60°, ∴△AGP是等边三角形, ∴∠AGC=60°=∠APG, ∴∠APE=60°, ∴∠EPC=60°, 连接EC,延长BC到F,使CF=PA,连接EF, ∵将△ABC绕点A逆时针旋转60°得到△ADE, ∴∠EAC=60°,∠EPC=60°, ∵AE=AC, ∴△ACE是等边三角形, ∴AE=EC=AC, ∵∠PAE+∠APE+∠AEP=180°,∠ECF+∠ACE+∠ACB=180°,∠ACE=∠APE=60°,∠AED=∠ACB, ∴∠PAE=∠ECF, 在△APE和△ECF中 ∴△APE≌△ECF(SAS), ∴PE=PF, ∴PA+PC=PE; (2)解:如图2:以MG为边作等边三角形△MGD,以OM为边作等边△OME.连接ND,作DF⊥NM,交NM的延长线于F. ∵△MGD和△OME是等边三角形 ∴OE=OM=ME,∠DMG=∠OME=60°,MG=MD, ∴∠GMO=∠DME 在△GMO和△DME中 ∴△GMO≌△DME(SAS), ∴OG=DE ∴NO+GO+MO=DE+OE+NO ∴当D、E、O、M四点共线时,NO+GO+MO值最小, ∵∠NMG=75°,∠GMD=60°, ∴∠NMD=135°, ∴∠DMF=45°, ∵MG=. ∴MF=DF=4, ∴NF=MN+MF=6+4=10, ∴ND===2, ∴MO+NO+GO最小值为2, 故答案为2, 【点评】本题考查了旋转的性质,等边三角形的性质,勾股定理,最短路径问题,构造等边三角形是解答本题的关键. 三、解答题(共8题,共72分) 17.(8分)计算:(2x2)3﹣x2•x4. 【分析】先算乘方与乘法,再合并同类项即可. 【解答】解:(2x2)3﹣x2•x4 =8x6﹣x6 =7x6. 【点评】本题考查了整式的混合运算,掌握运算性质和法则是解题的关键. 18.(8分)如图,点A、B、C、D在一条直线上,CE与BF交于点G,∠A=∠1,CE∥DF,求证:∠E=∠F. 【分析】根据平行线的性质可得∠ACE=∠D,又∠A=∠1,利用三角形内角和定理及等式的性质即可得出∠E=∠F. 【解答】解:∵CE∥DF, ∴∠ACE=∠D, ∵∠A=∠1, ∴180°﹣∠ACE﹣∠A=180°﹣∠D﹣∠1, 又∵∠E=180°﹣∠ACE﹣∠A,∠F=180°﹣∠D﹣∠1, ∴∠E=∠F. 【点评】本题考查了平行线的性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.也考查了三角形内角和定理. 19.(8分)为弘扬中华传统文化,某校开展“双剧进课堂”的活动,该校童威随机抽取部分学生,按四个类别:A表示“很喜欢”,B表示“喜欢”,C表示“一般”,D表示“不喜欢” ,调查他们对汉剧的喜爱情况,将结果绘制成如下两幅不完整的统计图,根据图中提供的信息,解决下列问题: (1)这次共抽取 50 名学生进行统计调查,扇形统计图中,D类所对应的扇形圆心角的大小为 72° ; (2)将条形统计图补充完整; (3)该校共有1500名学生,估计该校表示“喜欢”的B类的学生大约有多少人? 【分析】(1)这次共抽取:12÷24%=50(人),D类所对应的扇形圆心角的大小360°×=72°; (2)A类学生:50﹣23﹣12﹣10=5(人),据此补充条形统计图; (3)该校表示“喜欢”的B类的学生大约有1500×=690(人). 【解答】解:(1)这次共抽取:12÷24%=50(人), D类所对应的扇形圆心角的大小360°×=72°, 故答案为50,72°; (2)A类学生:50﹣23﹣12﹣10=5(人), 条形统计图补充如下 该校表示“喜欢”的B类的学生大约有1500×=690(人), 答:该校表示“喜欢”的B类的学生大约有690人; 【点评】本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小. 20.(8分)如图是由边长为1的小正方形构成的网格,每个小正方形的顶点叫做格点.四边形ABCD的顶点在格点上,点E是边DC 与网格线的交点.请选择适当的格点,用无刻度的直尺在网格中完成下列画图,保留连线的痕迹,不要求说明理由. (1)如图1,过点A画线段AF,使AF∥DC,且AF=DC. (2)如图1,在边AB上画一点G,使∠AGD=∠BGC. (3)如图2,过点E画线段EM,使EM∥AB,且EM=AB. 【分析】(1)作平行四边形AFCD即可得到结论; (2)根据等腰三角形的性质和对顶角的性质即可得到结论; (3)作平行四边形AEMB即可得到结论. 【解答】解:(1)如图所示,线段AF即为所求; (2)如图所示,点G即为所求; (3)如图所示,线段EM即为所求. 【点评】本题考查了作图﹣应用与设计作图,平行线四边形的判定和性质,等腰三角形的判定和性质,对顶角的性质,正确的作出图形是解题的关键. 21.(8分)已知AB是⊙O的直径,AM和BN是⊙O的两条切线,DC与⊙O相切于点E,分别交AM、BN于D、C两点. (1)如图1,求证:AB2=4AD•BC; (2)如图2,连接OE并延长交AM于点F,连接CF.若∠ADE=2∠OFC,AD=1,求图中阴影部分的面积. 【分析】(1)连接OC、OD,证明△AOD∽△BCO,得出=,即可得出结论; (2)连接OD,OC,证明△COD≌△CFD得出∠CDO=∠CDF,求出∠BOE=120°,由直角三角形的性质得出BC=3,OB=,图中阴影部分的面积=2S△OBC﹣S扇形OBE,即可得出结果. 【解答】(1)证明:连接OC、OD,如图1所示: ∵AM和BN是它的两条切线, ∴AM⊥AB,BN⊥AB, ∴AM∥BN, ∴∠ADE+∠BCE=180° ∵DC切⊙O于E, ∴∠ODE=∠ADE,∠OCE=∠BCE, ∴∠ODE+∠OCE=90°, ∴∠DOC=90°, ∴∠AOD+∠COB=90°, ∵∠AOD+∠ADO=90°, ∴∠AOD=∠OCB, ∵∠OAD=∠OBC=90°, ∴△AOD∽△BCO, ∴=, ∴OA2=AD•BC, ∴(AB)2=AD•BC, ∴AB2=4AD•BC; (2)解:连接OD,OC,如图2所示: ∵∠ADE=2∠OFC, ∴∠ADO=∠OFC, ∵∠ADO=∠BOC,∠BOC=∠FOC, ∴∠OFC=∠FOC, ∴CF=OC, ∴CD垂直平分OF, ∴OD=DF, 在△COD和△CFD中,, ∴△COD≌△CFD(SSS), ∴∠CDO=∠CDF, ∵∠ODA+∠CDO+∠CDF=180°, ∴∠ODA=60°=∠BOC, ∴∠BOE=120°, 在Rt△DAO,AD=OA, Rt△BOC中,BC=OB, ∴AD:BC=1:3, ∵AD=1, ∴BC=3,OB=, ∴图中阴影部分的面积=2S△OBC﹣S扇形OBE=2×××3﹣=3﹣π. 【点评】本题考查了相似三角形的判定与性质、切线的性质、全等三角形的判定与性质、扇形面积公式、直角三角形的性质等知识;证明三角形相似和三角形全等是解题的关键. 22.(10分)某商店销售一种商品,童威经市场调查发现:该商品的周销售量y(件)是售价x(元/件)的一次函数,其售价、周销售量、周销售利润w(元)的三组对应值如表: 售价x(元/件) 50 60 80 周销售量y(件) 100 80 40 周销售利润w(元) 1000 1600 1600 注:周销售利润=周销售量×(售价﹣进价) (1)①求y关于x的函数解析式(不要求写出自变量的取值范围); ②该商品进价是 40 元/件;当售价是 70 元/件时,周销售利润最大,最大利润是 1800 元. (2)由于某种原因,该商品进价提高了m元/件(m>0),物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求m的值. 【分析】(1)①依题意设y=kx+b,解方程组即可得到结论;[来源:学_科_网] ②该商品进价是50﹣1000÷100=40,设每周获得利润w=ax2+bx+c:解方程组即可得到结论; (2)根据题意得,w=(x﹣40﹣m)(﹣2x+200)=﹣2x2+(280+2m)x﹣800﹣200m,由于对称轴是x=,根据二次函数的性质即可得到结论. 【解答】解:(1)①依题意设y=kx+b, 则有 解得: 所以y关于x的函数解析式为y=﹣2x+200; ②该商品进价是50﹣1000÷100=40, 设每周获得利润w=ax2+bx+c: 则有, 解得:, ∴w=﹣2x2+280x﹣8000=﹣2(x﹣70)2+1800, ∴当售价是70元/件时,周销售利润最大,最大利润是1800元; 故答案为:40,70,1800; (2)根据题意得,w=(x﹣40﹣m)(﹣2x+200)=﹣2x2+(280+2m)x﹣800﹣200m, ∵对称轴x=, ∴①当<65时(舍),②当≥65时,x=65时,w求最大值1400, 解得:m=5. 【点评】本题考查了二次函数在实际生活中的应用,重点是掌握求最值的问题.注意:数学应用题来源于实践,用于实践,在当今社会市场经济的环境下,应掌握一些有关商品价格和利润的知识,总利润等于总收入减去总成本,然后再利用二次函数求最值. 23.(10分)在△ABC中,∠ABC=90°,=n,M是BC上一点,连接AM. (1)如图1,若n=1,N是AB延长线上一点,CN与AM垂直,求证:BM=BN. (2)过点B作BP⊥AM,P为垂足,连接CP并延长交AB于点Q. ①如图2,若n=1,求证:=. ②如图3,若M是BC的中点,直接写出tan∠BPQ的值.(用含n的式子表示) 【分析】(1)如图1中,延长AM交CN于点H.想办法证明△ABM≌△CBN(ASA)即可. (2)①如图2中,作CH∥AB交BP的延长线于H.利用全等三角形的性质证明CH=BM ,再利用平行线分线段成比例定理解决问题即可. ②如图3中,作CH∥AB交BP的延长线于H,作CN⊥BH于N.不妨设BC=2m,则AB=2mn.想办法求出CN,PN(用m,n表示),即可解决问题. 【解答】(1)证明:如图1中,延长AM交CN于点H. ∵AM⊥CN, ∴∠AHC=90°, ∵∠ABC=90°, ∴∠BAM+∠AMB=90°,∠BCN+∠CMH=90°, ∵∠AMB=∠CMH, ∴∠BAM=∠BCN, ∵BA=BC,∠ABM=∠CBN=90°, ∴△ABM≌△CBN(ASA), ∴BM=BN. (2)①证明:如图2中,作CH∥AB交BP的延长线于H. ∵BP⊥AM, ∴∠BPM=∠ABM=90°, ∵∠BAM+∠AMB=90°,∠CBH+∠BMP=90°, ∴∠BAM=∠CBH, ∵CH∥AB, ∴∠HCB+∠ABC=90°, ∵∠ABC=90°, ∴∠ABM=∠BCH=90°, ∵AB=BC, ∴△ABM≌△BCH(ASA), ∴BM=CH, ∵CH∥BQ, ∴==. ②解:如图3中,作CH∥AB交BP的延长线于H,作CN⊥BH于N.不妨设BC=2m,则AB=2mn. 则BM=CM=m,CH=,BH=,AM=m, ∵•AM•BP=•AB•BM, ∴PB=, ∵•BH•CN=•CH•BC, ∴CN=, ∵CN⊥BH,PM⊥BH, ∴MP∥CN,∵CM=BM, ∴PN=BP=, ∵∠BPQ=∠CPN, ∴tan∠BPQ=tan∠CPN===. 【点评】本题属于相似形综合题,考查了相似三角形的判定和性质,全等三角形的判定和性质,解直角三角形等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用参数解决问题,属于中考压轴题. 24.(12分)已知抛物线C1:y=(x﹣1)2﹣4和C2:y=x2 (1)如何将抛物线C1平移得到抛物线C2? (2)如图1,抛物线C1与x轴正半轴交于点A,直线y=﹣x+b经过点A,交抛物线C1于另一点B.请你在线段AB上取点P,过点P作直线PQ∥y轴交抛物线C1于点Q,连接AQ. ①若AP=AQ,求点P的横坐标; ②若PA=PQ,直接写出点P的横坐标. (3)如图2,△MNE的顶点M、N在抛物线C2上,点M在点N右边,两条直线ME、NE与抛物线C2均有唯一公共点,ME、NE均与y轴不平行.若△MNE的面积为2,设M、N两点的横坐标分别为m、n,求m与n的数量关系. 【分析】(1)y=(x﹣1)2﹣4向左评移1个单位长度,再向上平移4个单位长度即可得到y=x2; (2)易求点A(3,0),b=4,联立方程﹣x+4=(x﹣1)2﹣4,可得B(﹣,);设P(t,﹣t+4),Q(t,t2﹣2t﹣3), ①当AP=AQ时,则有﹣4+t=t2﹣2t﹣3,求得t=; ②当AP=PQ时,PQ=t2+t+7,PA=(3﹣t),则有t2+t+7=(3﹣t),求得t=﹣; (3)设经过M与N的直线解析式为y=k(x﹣m)+m2, ∴,则可知△=k2﹣4km+4m2=(k﹣2m)2=0,求得k=2m, 求出直线ME的解析式为y=2mx﹣m2,直线NE的解析式为y=2nx﹣n2,则可求E(,mn), 再由面积[(n2﹣mn)+(m2﹣mn)]×(m﹣n)﹣(n2﹣mn)×(﹣n)﹣(m2﹣mn)×(m﹣)=2,可得(m﹣n)3=8,即可求解; 【解答】解:(1)y=(x﹣1)2﹣4向左评移1个单位长度,再向上平移4个单位长度即可得到y=x2; (2)y=(x﹣1)2﹣4与x轴正半轴的交点A(3,0), ∵直线y=﹣x+b经过点A, ∴b=4, ∴y=﹣x+4, y=﹣x+4与y=(x﹣1)2﹣4的交点为﹣x+4=(x﹣1)2﹣4的解, ∴x=3或x=﹣, ∴B(﹣,), 设P(t,﹣t+4),且﹣<t<3, ∵PQ∥y轴, ∴Q(t,t2﹣2t﹣3), ①当AP=AQ时, |4﹣t|=|t2﹣2t﹣3|, 则有﹣4+t=t2﹣2t﹣3, ∴t=, ∴P点横坐标为; ②当AP=PQ时, PQ=t2+t+7,PA=(3﹣t), ∴t2+t+7=(3﹣t), ∴t=﹣; ∴P点横坐标为﹣; (3)设经过M与N的直线解析式为y=k(x﹣m)+m2, ∴, 则有x2﹣kx+km﹣m2=0, △=k2﹣4km+4m2=(k﹣2m)2=0, ∴k=2m, 直线ME的解析式为y=2mx﹣m2,直线NE的解析式为y=2nx﹣n2, ∴E(,mn), ∴[(n2﹣mn)+(m2﹣mn)]×(m﹣n)﹣(n2﹣mn)×(﹣n)﹣(m2﹣mn)×(m﹣)=2, ∴(m﹣n)2﹣=4, ∴(m﹣n)3=8, ∴m﹣n=2; 【点评】本题考查二次函数的图象及性质;是二次函数的综合题,熟练掌握直线与二次函数的交点求法,借助三角形面积列出等量关系是解决m与n的关系的关键. 声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布 日期:2019/6/26 18:00:29;用户:冯锡眉;邮箱:zxfengxm@xyh.com;学号:22634181查看更多