- 2021-11-10 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2012年浙江省台州市中考数学试题(含答案)
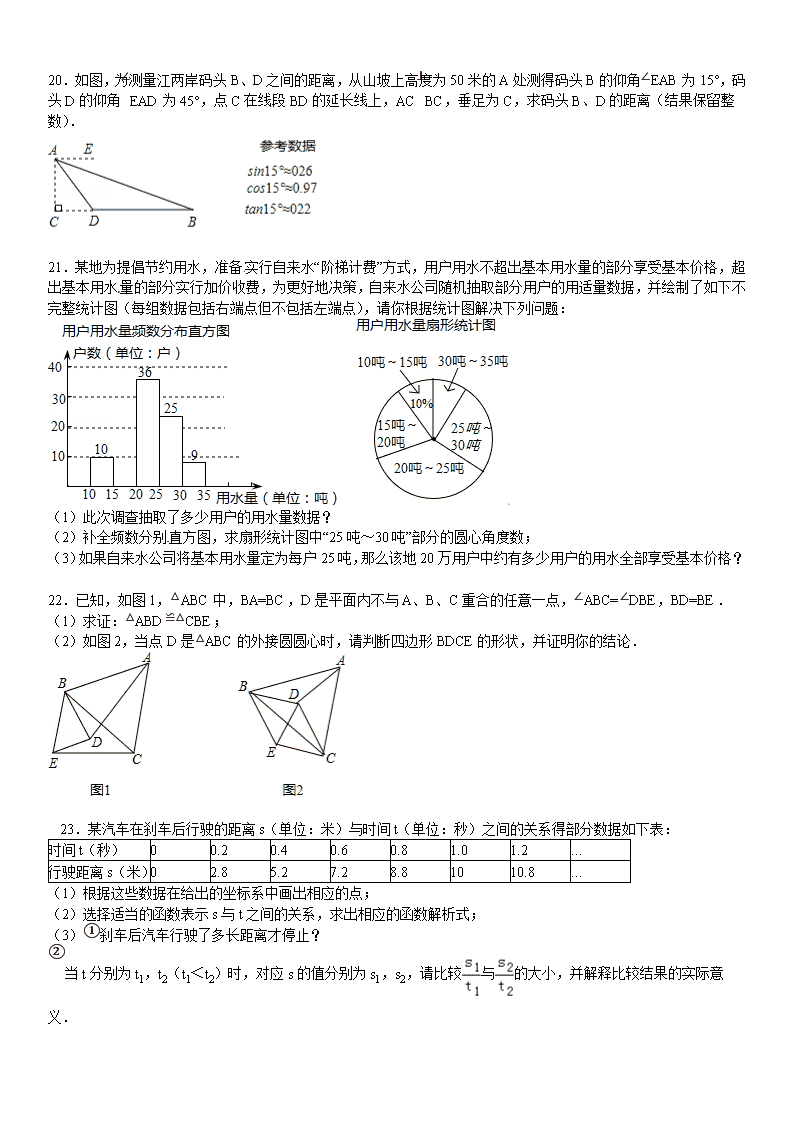
2012年浙江省台州市中考数学试卷 一. 选择题(共10小题) 1. 计算-1+1的结果是( ) A.1 B.0 C.-1 D.-2 2. 在下列四个汽车标志图案中,能用平移变换来分析其形成过程的图案是( ) A. B. C. D. 3.如图是一个由3个相同的正方体组成的立体图形,则它的主视图为( ) A. B. C. D. 4. 如图,点D、E、F分别为∠ABC三边的中点,若△DEF的周长为10,则△ABC的周长为( ) A.5 B.10 C.20 D.40 第6题 第4题 5. 计算(-2a)3的结果是( ) A .6a3 B.-6a3 C.8a3 D.-8a3 6. 如图,点A、B、C是⊙O上三点,∠AOC=130°,则∠ABC等于( ) A. 50° B.60° C.65° D.70° 7. 点(﹣1,y1),(2,y2),(3,y3)均在函数的图象上,则y1,y2,y3的大小关系是( ) A.y3<y2<y1 B.y2<y3<y1 C. y1<y2<y3 D.y1<y3<y2 8. 为了解某公司员工的年工资情况,小王随机调查了10位员工,其年工资(单位:万元)如下:3,3,3,4,5,5,6,6,8,20,下列统计量中,能合理反映该公司年工资中等水平的是( ) A.方差 B.众数 C.中位数 D.平均数 9. 小王乘公共汽车从甲地到相距40千米的乙地办事,然后乘出租车返回,出租车的平均速度比公共汽车多20千米/时,回来时路上所花时间比去时节省了,设公共汽车的平均速度为x千米/时,则下面列出的方程中正确的是( ) A. B. C. D. 10.如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( ) A. 1 B. C. 2 D. +1 二. 填空题(共6小题) 11.因式分解:m2-1=_________ 12.不透明的袋子里装有3个红球5个白球,它们除颜色外其它都相同,从中随机摸出一个球,则摸到红球的概率是__________. 13.计算的结果是 _________ . 14.如图,将正方形ABCD沿BE对折,使点A落在对角线BD上的A′处,连接A′C,则∠BA′C= _________ 度. 第16题 第14题 15.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=16厘米,则球的半径为 厘米. 16.请你规定一种适合任意非零实数a,b的新运算“a⊕b”,使得下列算式成立: 1⊕2=2⊕1=3,(﹣3)⊕(﹣4)=(﹣4)⊕(﹣3)=﹣,(﹣3)⊕5=5⊕(﹣3)=﹣,… 你规定的新运算a⊕b=______________(用a,b的一个代数式表示). 三. 解答题(共8小题) 17.计算: 18.解不等式组,并把解集在数轴上表示出来. 19.如图,正比例函数y=kx(x≥0)与反比例函数y=的图象交于点A(2,3), (1)求k,m的值; (2)写出正比例函数值大于反比例函数值时自变量x的取值范围. 20.如图,为测量江两岸码头B、D之间的距离,从山坡上高度为50米的A处测得码头B的仰角∠EAB为15°,码头D的仰角∠EAD为45°,点C在线段BD的延长线上,AC⊥BC,垂足为C,求码头B、D的距离(结果保留整数). 21.某地为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费,为更好地决策,自来水公司随机抽取部分用户的用适量数据,并绘制了如下不完整统计图(每组数据包括右端点但不包括左端点),请你根据统计图解决下列问题: (1)此次调查抽取了多少用户的用水量数据? (2)补全频数分别直方图,求扇形统计图中“25吨~30吨”部分的圆心角度数; (3)如果自来水公司将基本用水量定为每户25吨,那么该地20万用户中约有多少用户的用水全部享受基本价格? 22.已知,如图1,△ABC中,BA=BC,D是平面内不与A、B、C重合的任意一点,∠ABC=∠DBE,BD=BE. (1)求证:△ABD≌△CBE; (2)如图2,当点D是△ABC的外接圆圆心时,请判断四边形BDCE的形状,并证明你的结论. 源:Z*xx*k23.某汽车在刹车后行驶的距离s(单位:米)与时间t(单位:秒)之间的关系得部分数据如下表: 时间t(秒) 0 0.2 0.4 0.6 0.8 1.0 1.2 … 行驶距离s(米) 0 2.8 5.2 7.2 8.8 10 10.8 … (1)根据这些数据在给出的坐标系中画出相应的点; (2)选择适当的函数表示s与t之间的关系,求出相应的函数解析式; (3)①刹车后汽车行驶了多长距离才停止? ②当t分别为t1,t2(t1<t2)时,对应s的值分别为s1,s2,请比较与的大小,并解释比较结果的实际意义. 24. 定义:P,Q分别是两条线段a和b上任意一点,线段PQ长度的最小值叫做线段与线段的距离. 已知O(0,0),A(4,0),B(m,n),C(m+4,n)是平面直角系中四点. (1) 根据上述定义,当m=2,n=2时,如图1,线段BC与线段OA的距离是_____, 当m=5,n=2时,如图2,线段BC与线段OA的距离(即线段AB的长)为______ (2)如图3,若点B落在圆心为A,半径为2的圆上,线段BC与线段OA的距离记为d,求d关于m的函数解析式. (3)当m的值变化时,动线段BC与线段OA的距离始终为2,线段BC的中点为M. ①求出点M随线段BC运动所围成的封闭图形的周长; ②点D的坐标为(0,2),m≥0,n≥0,作MH⊥x轴,垂足为H,是否存在m的值,使以A,M,H为顶点的三角形与△AOD相似,若存在,求出m的值,若不存在,请说明理由. 参考答案 一.选择题 1B 2D 3A 4 C 5D 6C 7D 8C 9A 10B 一. 填空题 11. (m+1)(m-1) 12. 13.x2 14.67.5 15.10 16. 三. 解答题 17. 解:原式= 18. 解:解不等式①得,x>1, 解不等式②得,x<3, 故不等式的解集为:1<x<3, 在数轴上表示为: 19.解:(1)把(2,3)代入y=kx得:3=2k, ∴ k= 把(2,3)代入y= 得m=6; (2)由图象可知,当正比例函数值大于反比例函数值时, 自变量x的取值范围是x>2. 20. 解:∵AE∥BC,∴∠ADC=∠EAD=45° 又∵AC⊥CD,∴CD=AC=50 ∵AE∥BC ∴∠ABC=∠EAB=15° 又∵tan∠ABC= ∴[来源:Zxxk.Com] BC= ∴BD=185.2﹣50≈135(米) 答:码头B、D的距离约为135米. 21.解:(1)10÷10%=100(户); (2)100﹣10﹣36﹣25﹣9=100﹣80=20户,画直方图如图, (画图正确没标记数字同样给分,算出“15﹣﹣20吨”部分的用户数是20但没画图给1分) ×360°=90°; (3)×20=13.2(万户). 答:该地20万用户中约有13.2万户居民的用水全部享受基本价格. 22.(1)证明:∵∠ABC=∠DBE, ∴∠ABC+∠CBD=∠DBE+∠CBD, ∴∠ABD=∠CBE, 在△ABD与△CBE中, ∵,[来源:学科网] ∴△ABD≌△CBE (2)解:四边形BDEF是菱形.证明如下: 同(1)可证△ABD≌△CBE, ∴CE=AD, ∵点D是△ABC外接圆圆心, ∴DA=DB=DC, 又∵BD=BE, ∴BD=BE=CE=CD, ∴四边形BDCE是菱形 23.解:(1)描点图所示:(画图基本准确均给分); (2)由散点图可知该函数为二次函数 设二次函数的解析式为:s=at2+bt+c, ∵抛物线经过点(0,0), ∴c=0,[来源:学科网ZXXK] 又由点(0.2,2.8),(1,10)可得: 解得:a=﹣5,b=15; ∴二次函数的解析式为:s=﹣5t2+15t; 经检验,其余个点均在s=﹣5t2+15t上. (3)①汽车刹车后到停止时的距离即汽车滑行的最大距离, 当t=﹣时, 滑行距离最大, S= 即刹车后汽车行驶了 米才停止. ②∵s=﹣5t2+15t,∴s1=﹣5t12+15t1,s2=﹣5t22+15t2∴=﹣5t1+15; 同理=﹣5t2+15, ∴t1<t2,∴>, 其实际意义是刹车后到t2时间内的平均速到t1时间内的度小于刹车后平均速度. 24. 1)2, (2)4≤m≤6时 d=2 2≤m≤4时 d=[来源:Zxxk.Com] (3)①16+4π ②m=1 m=3 m=5.2查看更多