- 2021-11-07 发布 |
- 37.5 KB |
- 19页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2017-2018学年北京市海淀区九年级上期中数学试题含答案
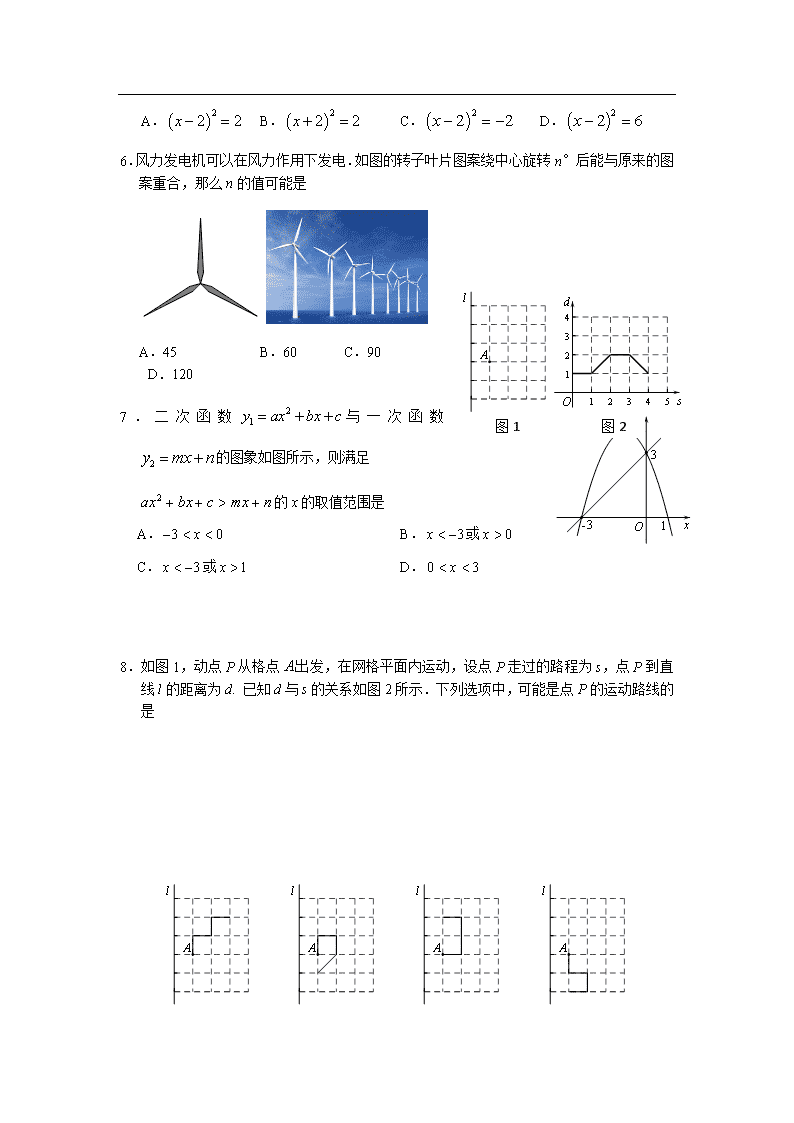
初三第一学期期中学业水平调研 数学 2017.11 学校班级___________姓名成绩 一、选择题(本题共24分,每小题3分) 下面各题均有四个选项,其中只有一个是符合题意的.请将正确选项前的字母填在表格中相应的位置. 题号 1 2 3 4 5 6 7 8 答案 1.一元二次方程的二次项系数、一次项系数、常数项分别是 A.3,6,1 B.3,6, C.3,,1 D.3,, 2.把抛物线向上平移1个单位长度得到的抛物线的表达式为 A. B. C. D. 3.如图,A,B,C是⊙O上的三个点. 若∠C=35°,则∠AOB的 大小为 A.35° B.55° C.65° D.70° 4.下列手机手势解锁图案中,是中心对称图形的是 A B C D 5.用配方法解方程,配方正确的是 A. B. C. D. 6.风力发电机可以在风力作用下发电.如图的转子叶片图案绕中心旋转n°后能与原来的图案重合,那么n的值可能是 A.45 B.60 C.90 D.120 7.二次函数与一次函数的图象如图所示,则满足 的x的取值范围是 A. B.或 C.或 D. 图1 图2 8.如图1,动点P从格点出发,在网格平面内运动,设点P走过的路程为s,点P到直线l的距离为d. 已知d与s的关系如图2所示.下列选项中,可能是点P的运动路线的是 A B C D 二、填空题(本题共24分,每小题3分) 9.点P(,2)关于原点的对称点的坐标为________. 10.写出一个图象开口向上,过点(0,0)的二次函数的 表达式:________. 11.如图,四边形ABCD内接于⊙,E为CD的延长线上一点. 若∠B=110°,则∠ADE的大小为________. 12.抛物线与x轴的公共点的个数是________. 13.如图,在平面直角坐标系xOy中,点A,点B的坐标分别 为(0,2),(,0),将线段AB绕点O顺时针旋转,若 点A的对应点的坐标为(2,0),则点B的对应点的 坐标为________. 14.已知抛物线经过点,,则 ________(填“>”,“=”,或“<”). 15.如图,⊙的半径OA与弦BC交于点D,若OD=3,AD=2, BD=CD,则BC的长为________. 16.下面是“作已知三角形的高”的尺规作图过程. 已知:△ABC. 求作:BC边上的高AD. 作法:如图, (1)分别以点A和点C为圆心,大于AC的 长为半径作弧,两弧相交于P,Q两点; (2)作直线PQ,交AC于点O; (3)以O为圆心,OA为半径作⊙O,与CB的延长线交于点D, 连接AD.线段AD即为所作的高. 请回答:该尺规作图的依据是_______________________________________________ . 三、解答题(本题共72分,第17题4分,第18~23题,每小题5分,第24~25题,每小题7分,第26~ 28题,每小题8分) 17.解方程:. 18.如图,等边三角形ABC的边长为3,点D是线段BC上的点,CD=2,以AD为边作等边三角形ADE,连接CE.求CE的长. 19.已知m是方程的一个根,求的值. 20.如图,在⊙O中,.求证:∠B=∠C. 21.如图,ABCD是一块边长为4米的正方形苗圃,园林部门拟将其改造为矩形AEFG的形状,其中点E在AB边上,点G在AD的延长线上,DG=2BE.设BE的长为x米,改造后苗圃AEFG的面积为y平方米. (1)y与x之间的函数关系式为_____________________(不需写自变量的取值范围); (2)根据改造方案,改造后的矩形苗圃AEFG的面积与原正方形苗圃ABCD的面积相等,请问此时BE的长为多少米? 22.关于的一元二次方程有两个不相等的实数根. (1)求实数的取值范围;[来源:Z§xx§k.Com] (2)是否存在实数,使得成立?如果存在,求出的值;如果不存在,请说明理由. 23.古代丝绸之路上的花剌子模地区曾经诞生过一位伟大的数学家——“代数学之父”阿尔·花拉子米.在研究一元二次方程解法的过程中,他觉得“有必要用几何学方式来证明曾用数字解释过的问题的正确性”. 以为例,花拉子米的几何解法如下: 如图,在边长为的正方形的两个相邻边上作边长分别为和 5的矩形,再补上一个边长为5的小正方形,最终把图形补 成一个大正方形. 通过不同的方式来表示大正方形的面积,可以将原方程化为 ,从而得到此方程的正根是________. 24.如图,在平面直角坐标系xOy中,点A的坐标为(1,0),点P的横坐标为2,将点A绕点P旋转,使它的对应点B恰好落在x轴上(不与A点重合);再将点B绕点O逆时针旋转90°得到点C. (1)直接写出点B和点C的坐标; (2)求经过A,B,C三点的抛物线的表达式. 25.如图,AB为⊙O的直径,点C在⊙O上,过点O作OD⊥BC交BC于点E,交⊙O于点D,CD∥AB. (1)求证:E为OD的中点; (2)若CB=6,求四边形CAOD的面积. 26.在平面直角坐标系中,已知抛物线C:和直线l:. (1)抛物线C的顶点D的坐标为________; (2)请判断点D是否在直线l上,并说明理由; (3)记函数的图象为G,点,过点垂直于 轴的直线与图象G交于点,.当时,若存在使得成立,结合图象,求的取值范围. 27.对于平面直角坐标系xOy中的点P,给出如下定义:记点P到x轴的距离为,到y轴的距离为,若,则称为点P的“引力值”;若,则称为点P的“引力值”.特别地,若点P在坐标轴上,则点P的“引力值”为0. 例如,点P(,3)到x轴的距离为3,到y轴的距离为2,因为,所以点P的“引力值”为2. (1)①点A(1,)的“引力值”为________; ②若点B(a,3)的“引力值”为2,则a的值为________; (2)若点C在直线上,且点C的“引力值”为2,求点C的坐标; (3)已知点M是以D(3,4)为圆心,半径为2的圆上的一个动点,那么点M的“引力值”d的取值范围是. 28.在Rt△ABC中,斜边AC的中点M关于BC的对称点为点O,将△ABC绕点O顺时针旋转至△DCE,连接BD,BE,如图所示. (1)在①∠BOE,②∠ACD,③∠COE中,等于旋转角的是________(填出满足条件的的角的序号); (2)若∠A=α,求∠BEC的大小(用含α的式子表示); (3)点N是BD的中点,连接MN,用等式表示线段MN与BE之间的数量关系,并证明. 初三第一学期期中学业水平调研 数学参考答案2017.11 一、选择题(本题共24分,每小题3分) 题号 1 2 3 4 5 6 7 8 答案 D A D B A D A D 二、填空题(本题共24分,每小题3分) 9.(1,) 10.答案不唯一,例如 11.110° 12.2 13.(0,1)14.>15.8 16.①到线段两端点距离相等的点在线段的垂直平分线上;②直径所对的圆周角是直角;③两点确定一条直线.(注:写出前两个即可给3分,写出前两个中的一个得2分,其余正确的理由得1分) 三、解答题(本题共72分) 17.解法一: 解:, ,………………2分 , ,.………………4分 解法二: 解:,………………2分 或, ,.………………4分 18.解:∵△ABC是等边三角形, ∴AB=BC=AC,∠BAC=60°. ∴∠1+∠3=60°.………………1分 ∵△ADE是等边三角形, ∴AD=AE,∠DAE=60°. ∴∠2+∠3=60°.………………2分 ∴∠1=∠2. 在△ABD与△ACE中 , ∴△ABD≌△ACE(SAS). ∴CE=BD.………………4分 ∵BC=3,CD=2, ∴BD=BC-CD=1. ∴CE=1.………………5分 19.解:∵m是方程的一个根, ∴.………………2分 ∴. ∴原式………………4分 .………………5分 20.方法1: 证明:∵在⊙O中,, ∴∠AOB=∠COD.………………2分 ∵OA=OB,OC=OD, ∴在△AOB中,, 在△COD中,.………………4分 ∴∠B=∠C.………………5分 方法2: 证明:∵在⊙O中,, ∴AB=CD.………………2分 ∵OA=OB,OC=OD, ∴△AOB≌△COD(SSS).………………4分 ∴∠B=∠C.………………5分 21.解:(1)(或)………………3分 (2)由题意,原正方形苗圃的面积为16平方米,得. 解得:,(不合题意,舍去).………………5分 答:此时BE的长为2米. 22.解:(1)∵方程有两个不相等的实数根, ∴, ∴.………………2分 (2)存在实数使得. ,即是说是原方程的一个根,则.………………3分 解得:或.………………4分 当时,方程为,有两个相等的实数根,与题意不符,舍去. ∴.………………5分 23.通过不同的方式来表示大正方形的面积,可以将原方程化为 ………………1分 ………………3分 从而得到此方程的正根是.………………5分 24.(1)点B的坐标为(3,0),点C的坐标为(0,3);………………2分 (2)方法1: 设抛物线的解析式为. 因为它经过A(1,0),B(3,0),C(0,3), 则………………4分 解得………………6分 ∴ 经过三点的抛物线的表达式为.………………7分 方法2: 抛物线经过点A(1,0),B(3,0),故可设其表达式为. ………………4分 因为点C(0,3)在抛物线上, 所以,得.………………6分 ∴经过三点的抛物线的表达式为.………………7分 方法3: 抛物线经过点A(1,0),B(3,0),则其对称轴为. 设抛物线的表达式为.………………4分[来源:学科网] 将A(1,0),C(0,3)代入,得 解得………………6分 ∴经过三点的抛物线的表达式为.………………7分 25.(1)证明: ∵在⊙O中,OD⊥BC于E, ∴CE=BE.………………1分 ∵CD∥AB,[来源:学科网ZXXK] ∴∠DCE=∠B.………………2分 在△DCE与△OBE中 ∴△DCE≌△OBE(ASA). ∴DE=OE. ∴E为OD的中点.………………4分 (2)解: 连接OC. ∵AB是⊙O的直径, ∴∠ACB=90°. ∵OD⊥BC, ∴∠CED=90°=∠ACB. ∴AC∥OD.………………5分 ∵CD∥AB, ∴四边形CAOD是平行四边形. ∵E是OD的中点,CE⊥OD, ∴OC=CD. ∵OC=OD, ∴OC=OD=CD. ∴△OCD是等边三角形. ∴∠D=60°.………………6分 ∴∠DCE=90°-∠D=30°. ∴在Rt△CDE中,CD=2DE. ∵BC=6, ∴CE=BE=3. ∵, ∴,. ∴. ∴.………………7分 26.(1)(2,0);………………2分 (2)点D在直线l上,理由如下: 直线l的表达式为, ∵当时,,………………3分 ∴点D(2,0)在直线l上.………………4分[来源:Zxxk.Com] 注:如果只有结论正确,给1分. (3)如图,不妨设点P在点Q左侧. 由题意知:要使得成立,即是要求点P与点Q关于直线对称. 又因为函数的图象关于直线对称, 所以当时,若存在使得成立,即要求点Q在的图象上.………………6分 根据图象,临界位置为射线过与的交点处,以及射线过与的交点处. 此时以及,故k的取值范围是.………………8分 27.(1)①1,②;………………2分 注:错一个得1分. (2)解:设点C的坐标为(x,y). 由于点C的“引力值”为2,则或,即,或. 当时,,此时点C的“引力值”为0,舍去; 当时,,此时C点坐标为(-2,8); 当时,,解得,此时点C的“引力值”为1,舍去; 当时,,,此时C点坐标为(3,-2); 综上所述,点C的坐标为(,8)或(3,).………………5分 注:得出一个正确答案得2分. (3).………………8分 注:答对一边给2分;两端数值正确,少等号给2分;一端数值正确且少等号给1分. 28.(1)③;………………1分 (2)连接BM,OB,OC,OE. ∵Rt△ABC中,∠ABC=90°,M为AC的中点, ∴MA=MB=MC=AC.………………2分 ∴∠A=∠ABM. ∵∠A=α, ∴∠BMC=∠A+∠ABM=2α. ∵点M和点O关于直线BC对称, ∴∠BOC=∠BMC=2α.………………3分 ∵OC=OB=OE, ∴点C,B,E在以O为圆心,OB为半径的圆上. ∴.………………4分 (3),证明如下: 连接BM并延长到点F,使BM=MF,连接FD. ∵∠A=α,∠ABC=90°, ∴∠ACB=90°-∠A=90°-α. ∴∠DEC=∠ACB=90°-α. ∵∠BEC=α, ∴∠BED=∠BEC+∠DEC=90°. ∵BC=CE, ∴∠CBE=∠CEB=α. ∵MB=MC, ∴∠MBC=∠ACB=90°-α. ∴∠MBE=∠MBC+∠CBE=90°. ∴∠MBE+∠BED=180°. ∴BF∥DE.………………6分 ∵BF=2BM,AC=2BM,[来源:学科网] ∴BF=AC. ∵AC=DE, ∴BF=DE. ∴四边形BFDE是平行四边形.………………7分 ∴DF=BE. ∵BM=MF,BN=ND, ∴MN=DF. ∴MN =BE.………………8分 注:如果只有结论正确,给1分. 解答题解法不唯一,如有其它解法相应给分.查看更多