2019年湖北省荆门市中考数学模拟试卷（含答案解析）

2019年湖北省荆门市中考数学模拟试卷（含答案解析）

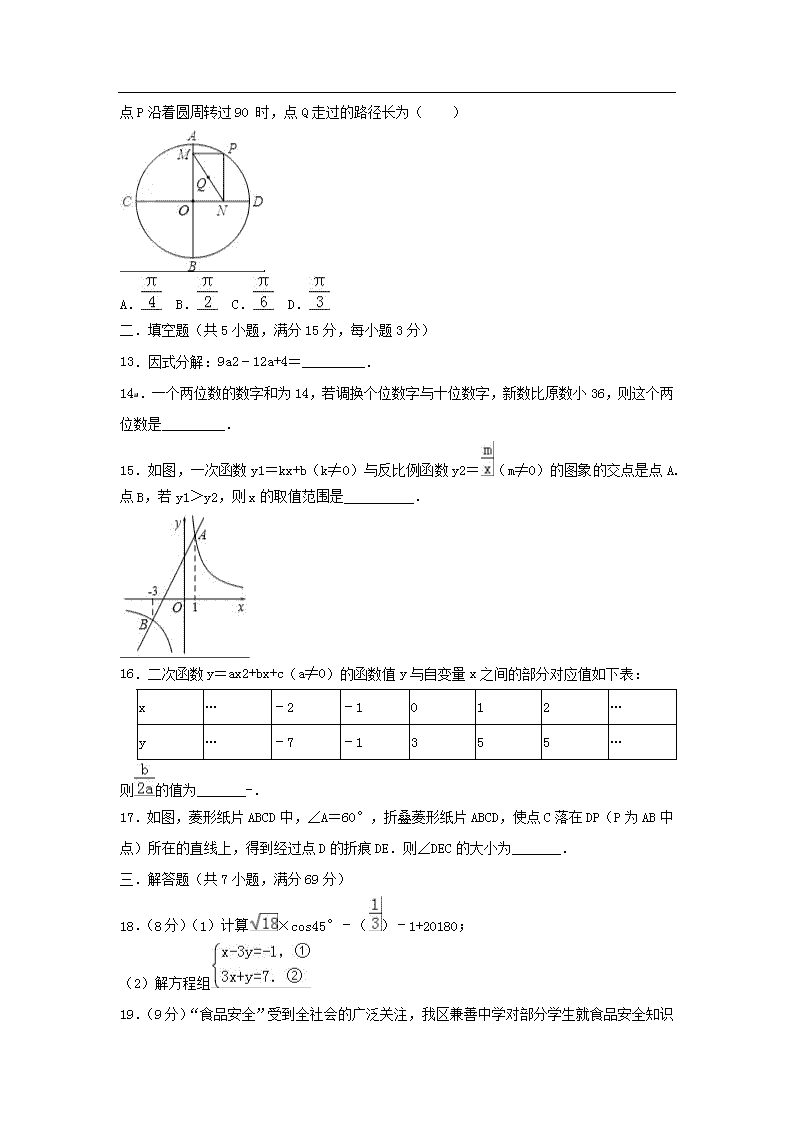
‎2019年湖北省荆门市中考数学模拟试卷 一．选择题（满分36分，每小题3分）‎ ‎1．若a2＝4，b2＝9，且ab＜0，则a﹣b的值为（　　）‎ A．﹣2 B．±5 C．5 D．﹣5‎ ‎2．下列运算正确的是（　　）‎ A．（x﹣y）2＝x2﹣y2 B．x2•x4＝x6 ‎ C． D．（2x2）3＝6x6‎ ‎3．世界上最小的鸟是生活在古巴的吸蜜蜂鸟，它的质量约为0.056盎司．将0.056用科学记数法表示为（　　）‎ A．5.6×10﹣1 B．5.6×10﹣2 C．5.6×10﹣3 D．0.56×10﹣1‎ ‎4．如图是由几个相同的正方体搭成的一个几何体，从正面看到的平面图形是（　　）‎ A． B． ‎ C． D．‎ ‎5．如图，已知AB∥DE，∠ABC＝75°，∠CDE＝145°，则∠BCD的值为（　　）‎ A．20° B．30° C．40° D．70°‎ ‎6．若x＝﹣4，则x的取值范围是（　　）‎ A．2＜x＜3 B．3＜x＜4 C．4＜x＜5 D．5＜x＜6‎ ‎7．关于x的一元二次方程x2﹣（k+3）x+k＝0的根的情况是（　　）‎ A．有两不相等实数根 B．有两相等实数根 ‎ C．无实数根 D．不能确定 ‎8．若关于x的不等式组有实数解，则a的取值范围是（　　）‎ A．a＜4 B．a≤4 C．a＞4 D．a≥4‎ ‎9．周末小丽从家里出发骑单车去公园，因为她家与公园之间是一条笔直的自行车道，所以小丽骑得特别放松．途中，她在路边的便利店挑选一瓶矿泉水，耽误了一段时间后继续骑行，愉快地到了公园．图中描述了小丽路上的情景，下列说法中错误的是（　　）‎ A．小丽从家到达公园共用时间20分钟 ‎ B．公园离小丽家的距离为2000米 ‎ C．小丽在便利店时间为15分钟 ‎ D．便利店离小丽家的距离为1000米 ‎10．已知x＝2是关于x的方程x2﹣（m+4）x+4m＝0的一个实数根，并且这个方程的两个实数根恰好是等腰三角形ABC的两条边长，则△ABC的周长为（　　）‎ A．6 B．8 C．10 D．8或10‎ ‎11．如图，在▱ABCD中，AB＝2，BC＝3．以点C为圆心，适当长为半径画弧，交BC于点P，交CD于点Q，再分别以点P，Q为圆心，大于PQ的长为半径画弧，两弧相交于点N，射线CN交BA的延长线于点E，则AE的长是（　　）‎ A． B．1 C． D．‎ ‎12．如图，☉O的半径为2，AB，CD是互相垂直的两条直径，点P是☉O上任意一点（点P与点A，B，C，D不重合），过点P作PM⊥AB于点M，PN⊥‎ CD于点N，点Q是MN的中点，当点P沿着圆周转过90 时，点Q走过的路径长为（　　）‎ ‎[‎ A． B． C． D．‎ 二．填空题（共5小题，满分15分，每小题3分）‎ ‎13．因式分解：9a2﹣12a+4＝_________．‎ ‎14．一个两位数的数字和为14，若调换个位数字与十位数字，新数比原数小36，则这个两位数是_________．‎ ‎15．如图，一次函数y1＝kx+b（k≠0）与反比例函数y2＝（m≠0）的图象的交点是点A.点B，若y1＞y2，则x的取值范围是__________．‎ ‎16．二次函数y＝ax2+bx+c（a≠0）的函数值y与自变量x之间的部分对应值如下表：‎ x ‎…‎ ‎﹣2‎ ‎﹣1‎ ‎0‎ ‎1‎ ‎2‎ ‎…‎ y ‎…‎ ‎﹣7‎ ‎﹣1‎ ‎3‎ ‎5‎ ‎5‎ ‎…‎ 则的值为_______-．‎ ‎17．如图，菱形纸片ABCD中，∠A＝60°，折叠菱形纸片ABCD，使点C落在DP（P为AB中点）所在的直线上，得到经过点D的折痕DE．则∠DEC的大小为_______．‎ 三．解答题（共7小题，满分69分）‎ ‎18．（8分）（1）计算×cos45°﹣（）﹣1+20180；‎ ‎（2）解方程组 ‎19．（9分）“食品安全”‎ 受到全社会的广泛关注，我区兼善中学对部分学生就食品安全知识的了解程度，采用随机抽样调查的方式，并根据收集到的信息进行统计，绘制了下面的两幅尚不完整的统计图，请你根据统计图中所提供的信息解答下列问题：‎ ‎（1）接受问卷调查的学生共有________人，扇形统计图中“基本了解”部分所对应扇形的圆心角为_________；‎ ‎（2）请补全条形统计图；[来源:Z*xx*k.Com]‎ ‎（3）若对食品安全知识达到“了解”程度的学生中，男、女生的比例恰为2：3，现从中随机抽取2人参加食品安全知识竞赛，请用树状图或列表法求出恰好抽到1个男生和1个女生的概率．‎ ‎20．（10分）已知，△ABC中，∠ACB＝90°，AC＝BC，点D为BC边上的一点．‎ ‎（1）以点C为旋转中心，将△ACD逆时针旋转90°，得到△BCE，请你画出旋转后的图形；‎ ‎（2）延长AD交BE于点F，求证：AF⊥BE；‎ ‎（3）若AC＝，BF＝1，连接CF，则CF的长度为_________．‎ ‎21．（10分）已知a＞0，符号[a]表示大于或等于a的最小正整数，如：[2，1]＝3，[4，8]＝5，[6]＝6，‎ ‎（1）填空：[7]＝　______，若[a]＝4，则a的取值范围______．‎ ‎（2）某地运输公司规定出租车的收费标准是：3公里以内（包括3公里）收费5元；超出的部分，每公里加收2元（不足1公里按1公里计算）．现在y表示乘客应付的乘车费（单位：元），用a表示所行驶的路程（单位：公里），则乘车费可按如下的公式计算：‎ ‎①当0＜a≤3时，y＝5；‎ ‎②当a＞3时，y＝5+2×[a﹣3]．‎ 某乘客乘车后付费15元，求该乘客所行驶的路程a（公里）的取值范围．‎ ‎22．（10分）如图，在一次军事演习中，蓝方在一条东西走向的公路上的A处朝正南方向撤 退，红方在公路上的B处沿南偏西60°方向前进实施拦截．红方行驶400米到达C处后，因前方无法通行，红方决定调整方向，再朝南偏西45°方向前进了相同的距离，刚好在D处成功拦截蓝方．求红蓝双方最初相距多远（参考数据：≈1.414，≈1.732，结果精确到个位）？‎ ‎23．（10分）如图，在等腰△ABC中，AB＝BC，以AB为直径的⊙O与AC相交于点D，过点D作DE⊥BC交AB延长线于点E，垂足为点F．‎ ‎（1）证明：DE是⊙O的切线；‎ ‎（2）若BE＝4，∠E＝30°，求由、线段BE和线段DE所围成图形（阴影部分）的面积，‎ ‎（3）若⊙O的半径r＝5，sinA＝，求线段EF的长．‎ ‎24．（12分）如图，已知抛物线y＝x2+3x﹣8的图象与x轴交于A，B两点（点A在点B的右侧），与y轴交于点C．‎ ‎（1）求直线BC的解析式；‎ ‎（2）点F是直线BC下方抛物线上的一点，当△BCF的面积最大时，在抛物线的对称轴上找一点P，使得△BFP的周长最小，请求出点F的坐标和点P的坐标；‎ ‎（3）在（2）的条件下，是否存在这样的点Q（0，m），使得△‎ BFQ为等腰三角形？如果有，请直接写出点Q的坐标；如果没有，请说明理由．‎ 参考答案 一．选择题 ‎1．解：∵a2＝4，b2＝9，‎ ‎∴a＝±2，b＝±3，‎ ‎∵ab＜0，‎ ‎∴a＝2，则b＝﹣3，‎ a＝﹣2，b＝3，‎ 则a﹣b的值为：2﹣（﹣3）＝5或﹣2﹣3＝﹣5．‎ 故选：B．‎ ‎2．解：∵（x﹣y）2＝x2﹣2xy+y2，故选项A错误；‎ ‎∵x2•x4＝x6，故选项B正确；‎ ‎∵＝3，故选项C错误；‎ ‎∵（2x2）3＝8x6，故选项D错误；‎ 故选：B．‎ ‎3．解：将0.056用科学记数法表示为5.6×10﹣2，‎ 故选：B．‎ ‎4．解：从正面看第一层是三个小正方形，第二层在中间位置一个小正方形，故D符合题意，‎ 故选：D．‎ ‎5．解：延长ED交BC于F，如图所示：‎ ‎∵AB∥DE，∠ABC＝75°，‎ ‎∴∠MFC＝∠B＝75°，‎ ‎∵∠CDE＝145°，‎ ‎∴∠FDC＝180°﹣145°＝35°，‎ ‎∴∠C＝∠MFC﹣∠MDC＝75°﹣35°＝40°，‎ 故选：C．‎ ‎6．解：∵36＜37＜49，‎ ‎∴6＜＜7，[来源:Z+xx+k.Com]‎ ‎∴2＜﹣4＜3，‎ 故x的取值范围是2＜x＜3．‎ 故选：A．‎ ‎7．解：△＝（k+3）2﹣4×k＝k2+2k+9＝（k+1）2+8，‎ ‎∵（k+1）2≥0，‎ ‎∴（k+1）2+8＞0，即△＞0，‎ 所以方程有两个不相等的实数根．‎ 故选：A．‎ ‎8．解：解不等式2x＞3x﹣3，得：x＜3，‎ 解不等式3x﹣a＞5，得：x＞，‎ ‎∵不等式组有实数解，‎ ‎∴＜3，‎ 解得：a＜4，‎ 故选：A．‎ ‎9．解：A.小丽从家到达公园共用时间20分钟，正确；‎ B.公园离小丽家的距离为2000米，正确；‎ C.小丽在便利店时间为15﹣10＝5分钟，错误；‎ D.便利店离小丽家的距离为1000米，正确；‎ 故选：C．‎ ‎10．解：把x＝2代入方程x2﹣（m+4）x+4m＝0得4﹣2（m+4）+4m＝0，解得m＝2，‎ 方程化为x2﹣6x+8＝0，解得x1＝4，x2＝2，‎ 因为2+2＝4，‎ 所以三角形三边为4.4.2，‎ 所以△ABC的周长为10．‎ 故选：C．‎ ‎11．解：∵由题意可知CE是∠BCD的平分线，‎ ‎∴∠BCE＝∠DCE．‎ ‎∵四边形ABCD是平行四边形，‎ ‎∴AB∥CD，‎ ‎∴∠DCE＝∠E，∠BCE＝∠AEC，‎ ‎∴BE＝BC＝3，‎ ‎∵AB＝2，‎ ‎∴AE＝BE﹣AB＝1，‎ 故选：B．‎ ‎12．解：如图连接OP．‎ ‎∵PM⊥AB于点M，PN⊥CD于点N，‎ ‎∴四边形ONPM是矩形，‎ 又∵点Q为MN的中点，‎ ‎∴点Q也是OP的中点，‎ 则OQ＝1，‎ 点Q走过的路径长＝＝．‎ 故选：B．[来源:Zxxk.Com]‎ 二．填空题（共5小题，满分15分，每小题3分）‎ ‎13．解：9a2﹣12a+4＝（3a﹣2）2．‎ ‎14．解：设原来十位上数字为x，个位上的数字为y，‎ 由题意得，，‎ 解得：，‎ 故这个两位数为95．‎ 故答案为；95．‎ ‎15．解：y1＞y2的自变量x的取值范围，从图上看就是一次函数图象在反比例函数图象上方时，横坐标x的取值范围，‎ 从图上看当x＞1或﹣3＜x＜0时一次函数图象在反比例函数图象上方，[来源:学。科。网]‎ 所以x＞1或﹣3＜x＜0时，y1＞y2．‎ 故答案为：x＞1或﹣3＜x＜0．‎ ‎16．解：∵x＝1.x＝2时的函数值都是﹣1相等，‎ ‎∴此函数图象的对称轴为直线x＝﹣＝＝，‎ 即＝﹣．‎ 故答案为：﹣．‎ ‎17．解：如图，连接BD，‎ ‎∵四边形ABCD为菱形，∠A＝60°，‎ ‎∴△ABD为等边三角形，∠ADC＝120°，∠C＝60°，‎ ‎∵P为AB的中点，‎ ‎∴DP为∠ADB的平分线，即∠ADP＝∠BDP＝30°，‎ ‎∴∠PDC＝90°，‎ ‎∴由折叠的性质得到∠CDE＝∠PDE＝45°，‎ 在△DEC中，∠DEC＝180°﹣（∠CDE+∠C）＝75°．‎ 故答案为：75°．‎ 三．解答题（共7小题，满分69分）‎ ‎18．解：（1）原式＝‎ ‎＝3﹣3+1‎ ‎＝1．‎ ‎（2）由①+②×3，得：10x＝20，‎ 解得：x＝2，‎ 把x＝2代入①，得：6+y＝1，‎ 解得：y＝1，‎ ‎∴原方程组的解为．‎ ‎19．解：（1）接受问卷调查的学生共有30÷50%＝60（人），‎ 扇形统计图中 “基本了解”部分所对应扇形的圆心角为360°×＝90°，‎ 故答案为：60，90．‎ ‎（2）了解的人数有：60﹣15﹣30﹣10＝5（人），补图如下：‎ ‎（3）画树状图得：‎ ‎​∵共有20种等可能的结果，恰好抽到1个男生和1个女生的有12种情况，‎ ‎∴恰好抽到1个男生和1个女生的概率为＝．‎ ‎20．（1）解：旋转后的图形如图所示．‎ ‎（2）证明：∵△ACD≌△BCE，‎ ‎∴∠CAD＝∠CBE，‎ ‎∵∠CAD+∠ADC＝90°，∠ADC＝∠BDF，‎ ‎∴∠BDF+∠DBF＝90°，‎ ‎∴∠DFB＝90°，‎ ‎∴AF⊥BE．‎ ‎（3）作CM⊥BE于M，CN⊥AF于N．‎ ‎∵∠ANC＝∠BMC＝90°，∠CAN＝∠CBM，AC＝BC，‎ ‎∴△ACN≌△BCM（AAS），‎ ‎∴CN＝CM，[来源:学科网]‎ ‎∵∠CMF＝∠MFN＝∠FNC＝90°，‎ ‎∴四边形CMFN是矩形，‎ ‎∵CM＝CN，‎ ‎∴四边形CMFN是正方形，设CN＝CM＝MF＝FN＝a，‎ 在Rt△BCM中，∵BC2＝CM2+BM2，‎ ‎∴3＝a2+（a+1）2，‎ ‎∴a2+a﹣1＝0，‎ ‎∴a＝或（舍弃），‎ ‎∴CF＝CM＝a＝．‎ 故答案为．‎ ‎21．解：（1）：[7]＝8；‎ 若[a]＝4，则x的取值范围是：3＜x≤4，‎ 故答案为：8.3＜x≤4．‎ ‎（2）根据题意可知5+2×[a﹣3]＝15．‎ 则[a﹣3]＝5，‎ ‎∴4＜a﹣3≤5，‎ 解得：7＜a≤8．‎ ‎22．解：过B作AB的垂线，过C作AB的平行线，两线交于点E；过C作AB的垂线，过D作AB的平行线，两线交于点F，则∠E＝∠F＝90°，红蓝双方相距AB＝DF+CE．‎ 在Rt△BCE中，‎ ‎∵BC＝400米，∠EBC＝60°，‎ ‎∴CE＝BC•sin60°＝400×＝200米．‎ 在Rt△CDF中，‎ ‎∵∠F＝90°，CD＝400米，∠DCF＝45°，‎ ‎∴DF＝CD•sin45°＝400×＝200米，‎ ‎∴AB＝DF+CE＝200+200≈629米．‎ 答：红蓝双方最初相距629米．‎ ‎23．解：（1）如图，连接BD.OD，‎ ‎∵AB是⊙O的直径，‎ ‎∴∠BDA＝90°，‎ ‎∵BA＝BC，‎ ‎∴AD＝CD，‎ 又∵AO＝OB，‎ ‎∴OD∥BC，‎ ‎∵DE⊥BC，‎ ‎∴OD⊥DE，‎ ‎∴DE是⊙O的切线；‎ ‎（2）设⊙O的半径为x，则OB＝OD＝x，‎ 在Rt△ODE中，OE＝4+x，∠E＝30°，‎ ‎∴＝，‎ 解得：x＝4，‎ ‎∴DE＝4，S△ODE＝×4×4＝8，‎ S扇形ODB＝＝，‎ 则S阴影＝S△ODE﹣S扇形ODB＝8﹣；‎ ‎（3）在Rt△ABD中，BD＝ABsinA＝10×＝2，‎ ‎∵DE⊥BC，‎ ‎∴Rt△DFB∽Rt△DCB，‎ ‎∴＝，即＝，‎ ‎∴BF＝2，‎ ‎∵OD∥BC，‎ ‎∴△EFB∽△EDO，‎ ‎∴＝，即＝，‎ ‎∴EB＝，‎ ‎∴EF＝＝．‎ ‎24．解：（1）对于抛物线y＝x2+3x﹣8，‎ 令y＝0，得到x2+3x﹣8＝0，解得x＝﹣8或2，‎ ‎∴B（﹣8，0），A（2，0），‎ 令x＝0，得到y＝﹣8，‎ ‎∴A（2，0），B（﹣8，0），C（0，﹣8），‎ 设直线BC的解析式为y＝kx+b，则有，‎ 解得，‎ ‎∴直线BC的解析式为y＝﹣x﹣8．‎ ‎（2）如图1中，作FN∥y轴交BC于N．设F（m， m2+3m﹣8），则N（m，﹣m﹣8）‎ ‎∴S△FBC＝S△FNB+S△FNC＝•FN×8＝4FN＝4[（﹣m﹣8）﹣（m2+3m﹣8）]＝﹣2m2﹣16m＝﹣2（m+4）2+32，‎ ‎∴当m＝﹣4时，△FBC的面积有最大值，‎ 此时F（﹣4，﹣12），‎ ‎∵抛物线的对称轴x＝﹣3，‎ 点B关于对称轴的对称点是A，连接AF交对称轴于P，此时△BFP的周长最小，‎ 设直线AF的解析式为y＝ax+b，则有，‎ 解得，‎ ‎∴直线AF的解析式为y＝2x﹣4，‎ ‎∴P（﹣3，﹣10），‎ ‎∴点F的坐标和点P的坐标分别是F（﹣4，﹣12），P（﹣3，﹣10）．‎ ‎（3）如图2中，‎ ‎∵B（﹣8，0），F（﹣4，﹣12），‎ ‎∴BF＝＝4，‎ ‎①当FQ1＝FB时，Q1（0，0）或（0，﹣24）（虽然FB＝FQ，但是B.F、Q三点一线应该舍去）．‎ ‎②当BF＝BQ时，易知Q2（0，﹣4），Q3（0，4）．‎ ‎③当Q4B＝Q4F时，设Q4（0，m），‎ 则有82+m2＝42+（m+12）2，‎ 解得m＝﹣4，‎ ‎∴Q4（0，﹣4），‎ ‎∴Q点坐标为（0，0）或（0，4）或（0，﹣4）或（0，﹣4）．‎