湘教版九年级数学上册期末测试题2（含答案）

湘教版九年级数学上册期末测试题2（含答案）

湘教版九年级数学上册期末测试题2（含答案）‎ ‎(考试时间：120分钟　　　满分：120分)‎ 第Ⅰ卷(选择题　共36分)‎ 一、选择题(每小题3分，共36分)‎ ‎1．点A(－1，1)是反比例函数y＝的图象上一点，则m的值为(　B　)‎ A．－1 B．－2 C．0 D．1‎ ‎2．在Rt△ABC中，cos A＝，那么tan A的值是(　D　)‎ A. B. C. D. 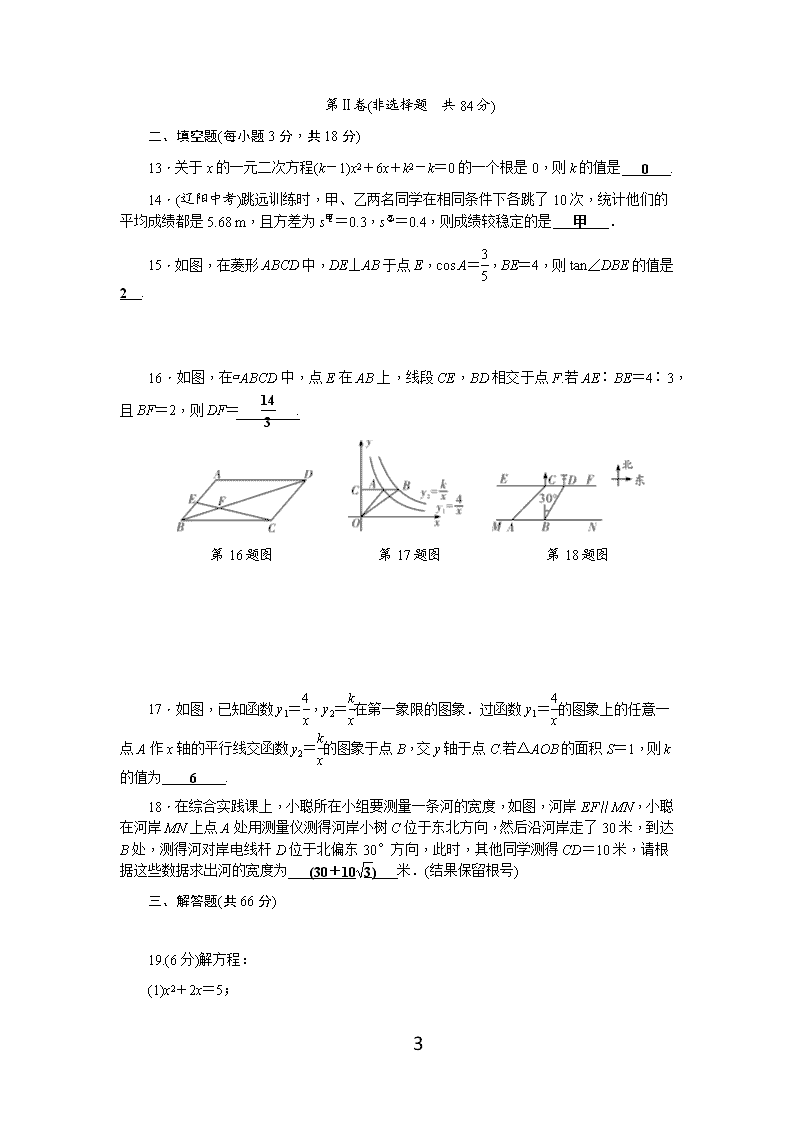‎3．某校九年级共有学生400人，为了解这些学生的视力情况，抽查了20名学生的视力，对所得数据进行整理，在得到的频数分布表中，若数据在0.95～1.15这一小组的频率为0.3，则可估计该校九年级学生视力在0.95～1.15范围内的人数约为(　D　)‎ A．6人 B．30人 C．60人 D．120人 ‎4．关于x的一元二次方程x2＋(a2－2a)x＋a－1＝0的两个实数根互为相反数，则a的值为(　B　)‎ A．2 B．0 C．1 D．2或0‎ ‎5．我们知道方程x2＋2x－3＝0的解是x1＝1，x2＝－3，现给出另一个方程(2x＋3)2＋2(2x＋3)－3＝0，它的解是(　D　)‎ A．x1＝1，x2＝3 B．x1＝1，x2＝－3‎ C．x1＝－1，x2＝3 D．x1＝－1，x2＝－3‎ ‎6．如图，在△ABC中，D，E分别为AB，AC边上的点，DE∥BC，点F为BC边上一点，连接AF交DE于点G，则下列结论中一定正确的是(　C　)‎ A.＝ B.＝ C.＝ D.＝ ‎　 　　 　　　‎ ‎　　　 第6题图　　　　　　　第8题图　　　　　　 第9题图 ‎7．一种药品原价每盒25元，经过两次降价后每盒16元，设两次降价的百分率都为x，则x满足(　D　)‎ 8‎ A．16(1＋2x)＝25 B．25(1－2x)＝16‎ C．16(1＋x)2＝25 D．25(1－x)2＝16‎ ‎8．如图所示，四边形ABCD与四边形AEFG是位似图形，且AC∶AF＝2∶3，则下列结论不正确的是(　B　)‎ A．四边形ABCD与四边形AEFG是相似图形 B．AD与AE的比是2∶3‎ C．四边形ABCD与四边形AEFG的周长比是2∶3‎ D．四边形ABCD与四边形AEFG的面积比是4∶9‎ ‎9．如图，已知点A，B分别在反比例函数y＝(x>0)，y＝－(x>0)的图象上，且OA⊥OB，则的值为(　B　)‎ A. B．2 C. D．4‎ ‎10．一人乘雪橇沿坡比为1∶的斜坡笔直滑下，滑下的距离s(m)与时间t(s)间的关系为s＝10t＋2t2.若滑到坡底的时间为4 s，则此人下降的高度为(　C　)‎ A．72 m B．36 m C．36 m D．18 m ‎11．如图，在平面直角坐标系xOy中，函数y＝kx＋b(k≠0)与y＝(m≠0)的图象相交于点A(2，3)，B(－6，－1)，则不等式kx＋b>的解集为(　B　)‎ A．x<－6 B．－62‎ C．x>2 D．x<－6或00，‎ x＝，‎ ‎∴x1＝，x2＝－4.‎ ‎20．(6分)计算下列各题：‎ ‎(1)tan 45°－sin 60°·cos 30°；‎ 解：原式＝1－× ＝1－＝；‎ ‎(2)sin230°＋sin 45°tan 30°.‎ 解：原式＝×＋× ＝.‎ ‎21．(8分)(宜宾中考)如图，一次函数y＝kx＋b的图象与反比例函数y＝的图象交于点A(－3，m＋8)，B(n，－6)两点．‎ ‎(1)求一次函数与反比例函数的表达式；‎ ‎(2)求△AOB的面积．‎ 解：(1)将A(－3，m＋8)代入反比例函数y＝得，＝m＋8，解得m＝－6，m＋8＝－6＋8＝2，所以点A的坐标为(－3，2)，反比例函数表达式为y＝－.将点B(n，－6)代入y＝－，得－＝－6，解得n＝1，所以，点B的坐标为(1，－6)．将点A(－3，2)，B(1，－6)，‎ 8‎ 代入y＝kx＋b，得解得所以，一次函数表达式为y＝－2x－4；‎ ‎(2)设AB与x轴相交于点C.令－2x－4＝0，解得x＝－2，所以，点C的坐标为(－2，0)，所以，OC＝2，S△AOB＝S△AOC＋S△BOC＝× 2× 2＋× 2× 6＝2＋6＝8.‎ ‎22．(8分)已知：如图，在菱形ABCD中，E为BC边上一点，∠AED＝∠B.‎ ‎(1)求证：△ABE∽△DEA；‎ ‎(2)若AB＝4，求AE·DE的值．‎ ‎(1)证明：∵四边形ABCD是菱形，‎ ‎∴AD∥BC，‎ ‎∴∠AEB＝∠DAE.‎ 又∵∠B＝∠AED，∴△ABE∽△DEA；‎ ‎(2)解：∵△ABE∽△DEA，‎ ‎∴＝，∴AE·DE＝AB·DA.‎ ‎∵四边形ABCD是菱形，AB＝4，‎ ‎∴AB＝DA＝4.‎ ‎∴AE·DE＝42＝16.‎ ‎23．(8分)(德州中考)随着移动终端设备的升级换代，手机已经成为我们生活中不可缺少的一部分．为了解中学生在假期使用手机的情况(选项A.和同学亲友聊天；B.学习 ；C.购物；D.游戏；E.其它)，端午节后某中学在全校范围内随机抽取了若干名学生进行调查，得到如下图表(部分信息未给出)：‎ ‎　　　‎ 8‎ 根据以上信息解答下列问题：‎ ‎(1)这次被调查的学生有多少人？‎ ‎(2)求表中m，n，p的值，并补全条形统计图；‎ ‎(3)若该中学约有800名学生，估计全校学生中利用手机购物或玩游戏的共有多少人？‎ 并根据以上调查结果，就中学生如何合理使用手机给出你的一条建议．‎ 解：(1)从C可以看出被调查的学生有：5÷ 0.1＝50人，‎ ‎(2)m＝＝0.2，n＝0.2× 50＝10，p＝0.4× 50＝20.‎ 补全条形统计图如图所示．‎ ‎(3)800×(0.1＋0.4)＝800× 0.5＝400人．‎ 合理即可，比如：中学生使用手机要多用于学习；中学生要少用手机玩游戏等．‎ ‎24．(10分)(眉山中考)东坡某烘焙店生产的蛋糕礼盒分为六个档次，第一档次(即最低档次)的产品每天生产76件，每件利润10元．调查表明：生产提高一个档次的蛋糕产品，该产品每件利润增加2元．‎ ‎(1)若生产的某批次蛋糕每件利润为14元，此批次蛋糕属第几档次产品；‎ ‎(2)由于生产工序不同，蛋糕产品每提高一个档次，一天产量会减少4件．若生产的某档次产品一天的总利润为1 080元，该烘焙店生产的是第几档次的产品？‎ 解：(1)若生产的某批次蛋糕每件利润为14元，此批蛋糕属第三档次．‎ ‎(2)设该烘焙店生产的是第x档次的产品，则每件利润为[10＋2(x－1)]元，每天产量为[76－4(x－1)]件，由题意得 ‎[10＋2(x－1)]·[76－4(x－1)]＝1 080，‎ x2－16x＋55＝0，‎ 解得x1＝5，x2＝11(舍去)．‎ ‎∴该烘焙店生产的是第五档次的产品．‎ ‎25．(10分)(黔东南州中考)如图，某校教学楼AB后方有一斜坡，已知斜坡CD的长为12米，坡角α为60°.根据有关部门的规定，∠α≤39°时，才能避免滑坡危险，学校为了消除安全隐患，决定对斜坡CD进行改造，在保持坡脚C不动的情况下，学校至少要把坡顶D向后水平移动多少米才能保证教学楼的安全？(结果取整数)(参考数据：sin 39°≈0.63，cos 39°≈0.78，tan 39°≈0.81，≈1.41，≈1.73，≈2.24)‎ 8‎ 解：假设点D移到D′的位置时，恰好∠α＝39°，过点D作DE⊥AC于点E，作D′E′⊥AC于点E′，‎ ‎∵CD＝12米，∠DCE＝60°，‎ ‎∴DE＝CD·sin 60°＝12× ＝6米，‎ CE＝CD·cos 60°＝12× ＝6米．‎ ‎∵DE⊥AC，D′E′⊥AC，DD′∥CE′，‎ ‎∴四边形DEE′D′是矩形，∴DE＝D′E′＝6米，‎ ‎∵∠D′CE′＝39°，∴CE′＝≈≈12.8，‎ ‎∴EE′＝CE′－CE＝12.8－6＝6.8≈7米．‎ 答：学校至少要把坡顶D向后水平移动7米才能保证教学楼的安全．‎ ‎26．(10分)(赤峰中考)如图，一次函数y＝－x＋1的图象与x轴，y轴分别交于点A，B，以线段AB为边在第一象限作等边△ABC.‎ ‎(1)若点C在反比例函数y＝的图象上，求该反比例函数的表达式；‎ ‎(2)点P(2，m)在第一象限，过点P作x轴的垂线，垂足为D，当△PAD与△OAB相似时，P点是否在(1)中反比例函数图象上？如果在，求出P点坐标；如果不在，请加以说明．‎ 解：(1)反比例函数表达式为y＝.‎ ‎(2)∵P(2，m)在第一象限，‎ ‎∴AD＝OD－OA＝2－＝，PD＝m，‎ 8‎ 当△ADP∽△AOB时，则有＝，即＝，解得m＝1，此时P点坐标为(2，1)；‎ 当△PDA∽△AOB时，则有＝，即＝，解得m＝3，‎ 此时P点坐标为(2，3)；‎ 把P(2，3)代入y＝可得3≠，‎ ‎∴P(2，3)不在反比例函数图象上，‎ 把P(2，1)代入反比例函数表达式得1＝，‎ ‎∴P(2，1)在反比例函数图象上；‎ 综上可知P点坐标为(2，1)．‎ 8‎