2010年朝阳区中考二模数学试题答案

2010年朝阳区中考二模数学试题答案

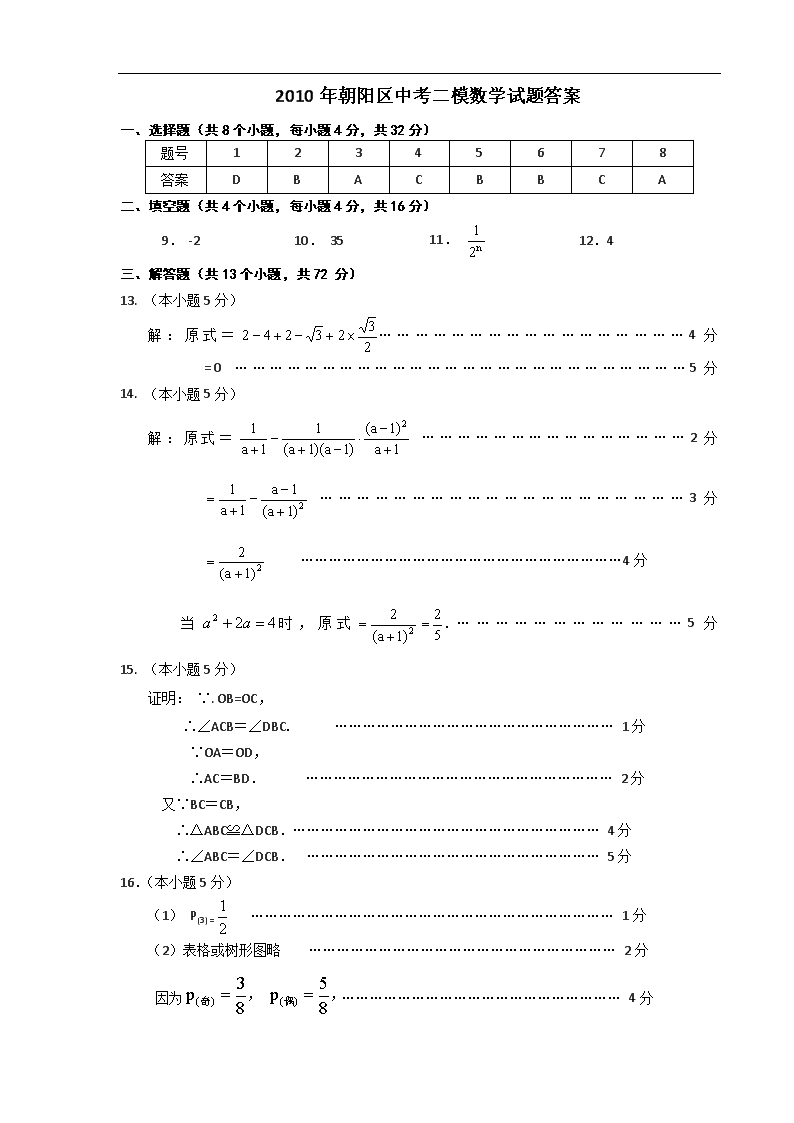
‎2010年朝阳区中考二模数学试题答案 ‎ 一、选择题（共8个小题，每小题4分，共32分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 答案 D B A C B B C A 二、填空题（共4个小题，每小题4分，共16分）‎ ‎9． -2‎ ‎10． 35‎ ‎11． ‎ ‎12．4‎ 三、解答题（共13个小题，共72 分） ‎ ‎13. （本小题5分）‎ 解：原式＝……………………………………………4分 ‎=0 ……………………………………………………………………5分 ‎14. （本小题5分）‎ 解：原式＝ ………………………………………2分 ‎ ……………………………………………………3分 ‎ ……………………………………………………………4分 ‎ 当时，原式.………………………………5分 ‎15. （本小题5分）‎ 证明： ∵. OB=OC，‎ ‎　∴∠ACB＝∠DBC.　　　…………………………………………………… 1分 ‎∵OA＝OD，‎ ‎∴AC＝BD．　　　………………………………………………………… 2分 又∵BC＝CB，‎ ‎ ∴△ABC≌△DCB．………………………………………………………… 4分 ‎∴∠ABC＝∠DCB．　……………………………………………………… 5分 ‎16．（本小题5分）‎ ‎（1） P(3) = …………………………………………………………………… 1分 ‎（2）表格或树形图略 ………………………………………………………… 2分 ‎ 因为 …………………………………………………… 4分 所以抽取的数字之和为偶数的概率大于数字之和为奇数的概率． ‎ 所以这个方案设计的不公平，李明的说法是正确的．………………………… 5分 ‎17．（本小题5分）‎ 解：（1）∵ 反比例函数（x＞0）的图象过点A，‎ ‎∴ k=6． ……………………………………………………………………… 1分 ‎∴ 反比例函数的解析式为． ………………………………………… 2分 ‎（2）∵ 点B在的图象上，且其横坐标为6，‎ ‎∴ 点B的坐标为（6，1）． ………………………………………………… 3分 设直线AB的解析式为，‎ 把点A和点B的坐标分别代入，‎ ‎ 解得 …………………………………………… 4分 ‎∴直线AB的解析式为 ……………………………………… 5分 ‎18. （本小题5分）‎ 解：设自行车的速度为x千米/时，则汽车的速度为4x千米/时，…………… 1分 由题意，得 ． ‎ 解得 x=15． ……………………………………………… 3分 经检验：x=15是原方程的解． ……………………………………………… 4分 则． ‎ 答：自行车的速度为‎15千米/时，则汽车的速度为‎60千米/时．……………… 5分 ‎19. （本小题5分）‎ 解：（1）如图1或 图2 ………………………………………………………… 2分 ‎ ‎ ‎（2）如图3 ……………………………………………………………………… 4分 过矩形ABCD的中心O1和平行四边形CBEF的中心O2画线段MN，交AD于M，交EF于N，‎ 则线段MN为所求． …………………………………………………… 5分 ‎20. （本小题5分）‎ 证明：（1）连接OD， ………………………… 1分 ‎∵OB＝OD，∴∠B＝∠1．‎ ‎∵AB=AC, ∴∠B=∠C．‎ ‎∴∠1=∠C．‎ ‎∴OD∥AC． ………………………… 2分 ‎ ‎∵DE⊥CF于点E，∴∠CED＝90°．‎ ‎∴∠ODE＝∠CED＝90°．‎ ‎∴ DE是⊙O的切线．………………………… 3分 解：(2) 连接AD，‎ ‎∵AB是⊙O的直径，∴∠ADB＝90°．‎ ‎∵cosC=cosB=．‎ ‎∵AB=10，∴BD=AB·cosB=8． …………………………………………… 4分 ‎∵∠F=∠B =∠C．‎ ‎∴DF=DC=8．且cosF=cosC=．‎ 在Rt△DEF中，‎ EF=DF·cosF=． …………………………………………………………… 5分 ‎21．（本小题5分）‎ 解：（1）34． ………………………………………………………………… 2分 ‎（2）∵，‎ ‎∴‎ ‎ =4+6=10． ………………………………………………………… 4分 ‎∴‎ ‎ =100-18=82．……………………………………………………… 5分 ‎22．（本小题5分）‎ 解：∵抛物线与直线相交，‎ ‎∴．…………………………………………………………1分 ‎∴．‎ ‎∴．‎ 解得 ．…………………………………………………………………… 2分 ‎∵， ∴． …………………………………………………… 3分 ‎∵ m为整数，∴ m=0，1．‎ ‎∵抛物线与直线交点的横坐标均为整数，‎ 即方程的根为整数．‎ 当m=0时，x2-2x=0，‎ 解得 x=0或x=2，两根均为整数，∴m=0符合题意． ……………………… 4分 当m=1时，，‎ ‎∵ △=(-4)2-4=12， ‎ ‎∴ x2-4x+1=0没有整数根，∴m=1不符合题意，舍去． ‎ ‎∴ 满足条件的m的整数值为0．………………………………………………… 5分 ‎23. （本小题7分）‎ 解：（1）①当 0 < t ≤ 2时,如图1，‎ 过点B作BE⊥DC，交DC的延长线于点E，‎ ‎∵∠BCE=∠D=60°，∴BE=4．‎ ‎∵ CP=t，‎ ‎∴ ． …………………………………… 2分 ‎② 当 2 < t ≤ 4时,如图2，‎ CP=t，BQ=2t-4，CQ=8-(2t-4)=12-2t． ‎ 过点P作PF⊥BC，交BC的延长线于点F．‎ ‎∵∠PCF=∠D=60°，∴PF=．‎ ‎∴ ．…………………… 4分 ‎（2）当 0 < t ≤ 2时,t=2时，S有最大值4．‎ 当 2< t ≤ 4时, ，‎ t=3时，S有最大值．‎ 综上所述，S的最大值为． ………………………………………………… 5分 ‎（3）当 0 < t ≤ 2时, △CPQ不是等腰三角形，‎ ‎∴ 不存在符合条件的菱形．…………………………………………………… 6分 ‎ 当 2 < t ≤ 4时,令CQ=CP，即t=12-2t，解得t=4．‎ ‎∴ 当t=4时，△CPQ是等腰三角形．‎ 即当t=4时，以△CPQ一边所在直线为轴翻折，翻折前后的两个三角形所组成的四边形为菱形． ………………………………………………………………………… 7分 ‎24. （本小题7分）‎ 解：（2）EF=DF-BE．……………………………………………………………… 1分 ‎（3）EF=DF-BE．…………………………………………………………………… 2分 证明：在DF上截取DM=BE，连接AM．如图，‎ ‎∵∠D+∠ABC=∠ABE+∠ABC=180°,‎ ‎∴∠D=∠ABE．‎ ‎∵AD=AB，‎ ‎∴△ADM≌△ABE．‎ ‎∴AM=AE．……………………………3分 ‎∴∠DAM=∠BAE．‎ ‎∵∠EAF=∠BAE+∠BAF=∠BAD，‎ ‎∴∠DAM+∠BAF=∠BAD．‎ ‎∴∠MAF=∠BAD．‎ ‎∴∠EAF=∠MAF． ………………………………………………………… 4分 ‎∵AF是△EAF与△MAF的公共边，‎ ‎∴△EAF≌△MAF．‎ ‎∴EF=MF．‎ ‎∵MF=DF-DM=DF-BE,‎ ‎∴EF=DF-BE． …………………………………………………………… 5分 ‎(4) △CEF的周长为15． ………………………………………………… 7分 ‎25. （本小题8分）‎ 解：（1）由题意，可得点B（2,2）．‎ ‎∵ CF=1， ∴ F ( 3，0 ) ．‎ 在正方形ABCD中，∠ABC=∠OAB=∠BCF＝90°，AB=AC，‎ ‎∵ BE⊥BF，∴∠EBF＝90°．‎ ‎∴∠EBF=∠ABC．即∴∠ABE+∠EBC=∠EBC+∠CBF．‎ ‎∴∠ABE=∠CBF．‎ ‎∴△ABE≌△CBF．‎ ‎∴ AE=CF．‎ ‎∴ E(0,1) ． ………………………………………………………………………… 1分 设过点E、B、F的抛物线的解析式为y=ax2+bx+1，‎ ‎∴ ∴‎ ‎∴抛物线的解析式为y=x2 +x +1． …………………………………… 2分 图1‎ ‎（2）∵ 点G(,y )在抛物线y=x2 +x +1上，‎ y=×()2 +×+1=．‎ ‎∴ G (,)．‎ 设过点B、G的直线解析式为y=kx+b,‎ ‎ ∴ ∴ ‎ ‎∴ 过点B、G的直线解析式为y=x+3．‎ ‎∴ 直线y=x+3与y轴交于点M (0,3) ． ………………………………… 3分 ‎∴ EM=2．‎ 可证∴△ABM≌△CBN．∴CN=AM．∴N (1,0) ． ∴ON=1．‎ ‎∴ EM=2ON．…………………………………………………………………… 4分 图2‎ ‎（3）∵ 点P在抛物线y=x2 +x +1上，‎ 可设点P坐标为（m，m2 +m +1）．‎ 如图2‎ ‎①过点P1作P1H1⊥y轴于点H1，连接P1E．‎ ‎∴ tan∠H1EP1=，∴．‎ 即 ．…… 5分 解得m1=,m2=0（不合题意，舍去）．‎ ‎②过点P2作P2H2⊥y轴于点H2，连接P2E．‎ ‎∴ tan∠H2EP2=，∴．‎ 即 ． ………………………………………… 6分 解得m3=,m4=0（不合题意，舍去）．‎ ‎ 当m1=时，m2 +m +1=；‎ ‎ 当m3=时, m2 +m +1=．‎ ‎ 综上所述，点P1（，），P2（，）为所求．…………………… 8分 说明：各解答题不同的正确解法参照以上标准给分.‎