2005年山东枣庄数学中考卷

2005年山东枣庄数学中考卷

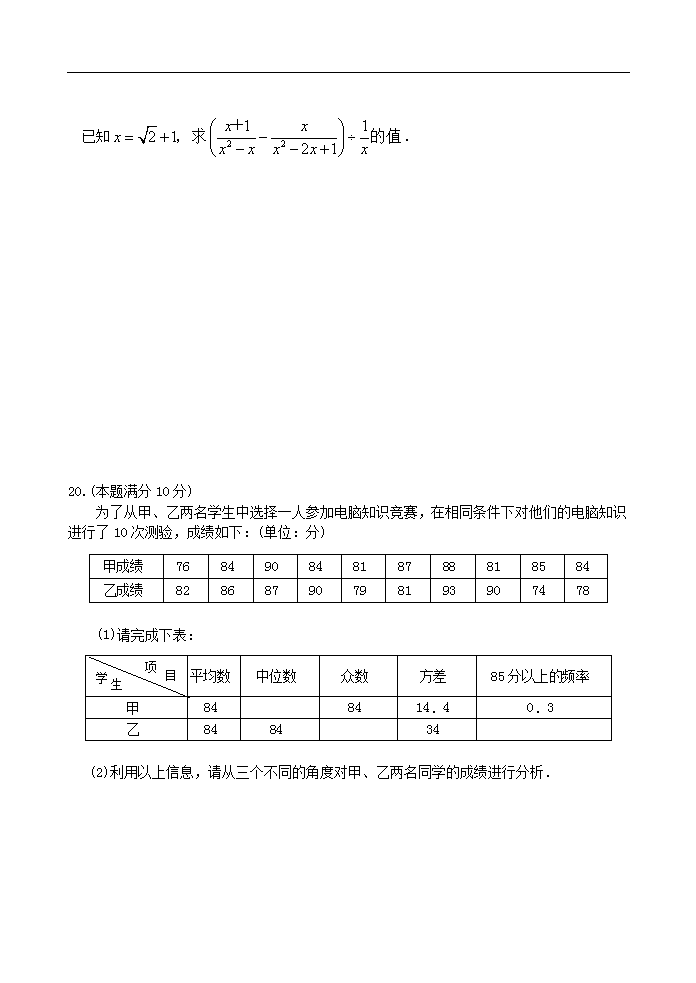
‎5.班级组织有奖知识竞赛，小明用100元班费购买笔记本和钢笔共30件，已知笔记本每本2元，钢笔每支5元，那么小明最多能买钢笔( )‎ ‎ (A)20支 (B)14支 (C)13支 (D)10支 ‎6.如图，小正方形的边长均为l，则下列图中的三角形(阴影部分)与△ABC相似的是( )‎ ‎7.如图，甲为四等分数字转盘，乙为三等分数字转盘．同时自由转动两个转盘，当转盘停止转动后(若指针指在边界处则重转)，两个转盘指针指向数字之和不超过4的概率是( )‎ ‎(A) (B) (C) (D) ‎ ‎8.如图，△ABC中，∠ABC＝∠BAC，D是AB的中点，EC∥AB，DE∥BC，AC与DE交于点O．下列结论中，不一定成立的是( )‎ ‎(A)AC＝DE (B)AB＝AC (C)AD＝EC (D)OA＝OE ‎9．如图，把直线ｌ沿x轴正方向向右平移2个单位得到直线ｌ′，则直线l/的解析式为( )‎ ‎(A)y=2x+4 (B)y=-2x+2 (C)y=2x-4 (D)y=-2x-2‎ ‎10．一个几何体由一些小正方体摆成，其主(正)视图与左视图如图所示．其俯视图不可能 是(　　)‎ ‎11．在直角坐标系中，0为坐标原点，A(1，1)，在x轴上确定一点P，使△AOP为等腰三角 形，则符合条件的点P共有( )‎ ‎ (A)1个 (B)2个 (C)3个 (D)4个 ‎12．水池有2个进水口，1个出水口，每个进水口进水量与时间的关系如图甲所示，出水口出水量与时间的关系如图乙所示．某天0点到6点，该水池的蓄水量与时间的关系如图丙所示．‎ 下列论断：①0点到1点，打开两个进水口，关闭出水口；②1点到3点，同时关闭两个进水口和—个出水口；③3点到4点，关门两个进水口，打开出水口；④5点到 ‎6点．同时打开两个进水口和一个出水口．其中，可能正确的论断是 ‎(A)①③ (B)①④ (C)②③ (D)②④‎ 第Ⅱ卷(非选择题 共98分)‎ ‎ 注意事项：‎ ‎ 1.第Ⅱ卷共8页，用钢笔或圆珠笔直接答在试卷上．‎ ‎ 2.答卷前将密封线内的项目填写清楚，并在右下角写清座号．‎ 二、填空题：本大题共6小题，共24分，只要求填写最后结果，每小题填对得4分．‎ ‎13.台湾是我国最大的岛屿，总面积为35 989.76平方千米，这个数据用科学记数法表示为______平方千米(保留两个有效数字)．‎ ‎14.方程x2－4x－3＝0的解为______.‎ ‎15.已知等腰△ABC内接于半径为5的⊙O，如果底边BC的长为8，那么BC边上的高为______.‎ ‎16.100个数排成一行，其中任意三个相邻数中，中间一个数都等于它前后两个数的和，如果这100个数的前两个数依次为1，0，那么这100个数中“‎0”‎的个数为 ___个． ‎ ‎17.如图，直线y＝－2x－2与双曲线交于点A，与x轴，y轴分别交于点B，C，AD⊥x轴于点D，如果S△ADB=S△COB，那么k=______·‎ ‎18.在平面直角坐标系中，横坐标、纵坐标都为整数的点称为整点．观察图中每一个正方形(实线)四条边上的整点的个数，请你猜测由里向外第10个正方形(实线)四条边上的整点个数共有_______个．‎ 三、解答题：本大题共7小题，共74分．解答要写出必要的文字说明、证明过程或演算步骤．‎ ‎19.(本题满分8分) 已知.‎ ‎20.(本题满分10分)‎ 为了从甲、乙两名学生中选择一人参加电脑知识竞赛，在相同条件下对他们的电脑知识进行了10次测验，成绩如下：(单位：分)‎ 甲成绩 ‎76‎ ‎84‎ ‎90‎ ‎84‎ ‎81‎ ‎87‎ ‎88‎ ‎81‎ ‎85‎ ‎84‎ 乙成绩 ‎82‎ ‎86‎ ‎87‎ ‎90‎ ‎79‎ ‎81‎ ‎93‎ ‎90‎ ‎74‎ ‎78‎ ‎(1)请完成下表：‎ 项 目 学 生 平均数 中位数 众数 方差 ‎85分以上的频率 甲 ‎84‎ ‎84‎ ‎14．4‎ ‎0．3‎ 乙 ‎84‎ ‎84‎ ‎34‎ ‎ (2)利用以上信息，请从三个不同的角度对甲、乙两名同学的成绩进行分析．‎ ‎21.(本题满分10分)‎ 如图，在⊙O中，弦AB与DC相交于点E，AB=CD．‎ ‎(1)求证：△AEC≌△DEB；‎ ‎(2)点B与点C关于直线OE对称吗?试说明理由．‎ ‎22.(本题满分10分) ‎ 已知抛物线的图象的一部分如图所示，抛物的顶点在第一象限，且经过点A(0，-7)和点B.‎ ‎ (1)求a的取值范围；‎ ‎ (2)若OA=2OB，求抛物线的解析式．‎ ‎23．(本题满分12分)‎ 某水果批发市场香蕉的价格如下表：‎ 购买香蕉数 ‎(千克)‎ 不超过 ‎20千克 ‎20千克以上但不超过40千克 ‎40千克以上 每千克价格 ‎6元 ‎5元 ‎4元 ‎ 张强两次共购买香蕉50千克(第二次多于第一次)，共付款264元，请问张强第一次、第二次分别购买香蕉多少千克?‎ ‎24．(本题满分12分)‎ ‎ 如图甲，四边形ABCD是等腰梯形，AB∥DC．由4个这样的等腰梯形可以拼出图乙所示的平行四边形。‎ ‎(1)求四边形ABCD四个内角的度数；‎ ‎ (2)试探究四边形ABCD四条边之间存在的等量关系，并说明理由；‎ ‎ (3)现有图甲中的等腰梯形若干个，利用它们你能拼出一个菱形吗?若能，请你画出大致的示意图．‎ ‎25．(本题满分12分)‎ ‎ 如图，在正方形ABCD中，AB=2，E是AD边上一点(点E与点A，D不重合)．BE的垂直平分线交AB于M，交DC于N．‎ ‎ (1)设AE=x，四边形ADNM的面积为S，写出S关于x的函数关系式；‎ ‎ (2)当AE为何值时，四边形ADNM的面积最大?最大值是多少?‎ ‎2005年中等学校招生考试数学试题 参考答案及评分标准 一、选择题：本大题共12小题，1～8题每小题选对得4分，9～12题每小题选对得 ‎5分，选错、不选或选出的答案超过一个均记零分.‎ ACBBC BDBCC DD 二、填空题：本大题共6小题，共24分，每小题填对得4分.‎ ‎ ‎13. 3.6‎×104 14. 15. 2或8 16. 33‎ ‎17．-4 18．40‎ ‎ 三、解答题：以下各题仅给出一种解(证)法，其它解(证)法，可参照本标准酌情赋分.‎ ‎19．解：原式；　　　　　　　　　　　　　　　　　　　　　………5分 ‎ 当时,　原式＝.　　　　　　　　　 　　………………………8分 ‎20．解：（1）‎ 项 目 学 生 平均数 中位数 众数 方差 ‎85分以上的频率 甲 ‎84‎ ‎84‎ ‎84‎ ‎14.4‎ ‎0.3‎ 乙 ‎84‎ ‎84‎ ‎90‎ ‎34‎ ‎0.5‎ ‎……………4分 ‎(2)甲成绩的众数是84，乙成绩的众数是90，从两人成绩的众数看，乙的成绩较好. …………………………………………………………………6分 ‎ 甲成绩的方差是14.4，乙成绩的方差是34，从成绩的方差看，甲的成绩相对稳定． ………………………………………………………………8分 ‎ 甲成绩、乙成绩的中位数、平均数都是84，但从85分以上的频率看，乙的成绩较好． ……………………………………………………10分 ‎21．解：(1)∵AB=CD， ∴＝． ‎ ‎ ∴ -=-． ‎ ‎ ∴=． ∴BD=CA. …………………3分 ‎ 在△AEC与△DEB中，∠ACE=∠DBE，∠AEC=∠DEB，‎ ‎ ∴△AEC≌△DEB ……………………………………………5分 ‎ (2)点B与点C关于直线OE对称. ……………………………7分 ‎ 理由如下：‎ ‎ 由(1)得BE＝CE， ∴点E在直线BC的中垂线上.‎ ‎ 连结BO，CO．‎ ‎ ∵BO＝CO， ∴点O在线段BC的中垂线上.‎ ‎ ∴直线EO是线段BC的中垂线.‎ ‎ ∴点B与点C关于直线OE对称． ………………………10分 ‎22．解：(1)由图可知，b=-7. …………………………………1分 故抛物线为y=(1-a)x2+8x-7又抛物线的顶点在第一象限，开口向下，所以抛物线与x轴有两个不同的交点．‎ ‎∴ 解之，得 . ………………3分 ‎ 即a的取值范围是. ………………6分 ‎ (2)设B(x1，o)，由OA=20B，得7=2x1，，即. ………………7分 由于，方程(1-a)x2+8x-7=0的一个根，‎ ‎∴ ‎ ‎ ∴. …………………………………9分 ‎ 故所求所抛物线解析式为. …………10分 ‎ 23．解：设张强第一次购买香蕉x千克，第二次购买香蕉y千克．由题意，得 ‎ 040时，由题意，得 ‎(不合题意，舍去)． ……………8分 ③ 当20

查看更多