人教版九年级上册数学期末测试题附答案1
人教版九年级上册数学期末测试题附答案1
(时间:120分钟 满分:120分)
姓名:______ 班级:______ 分数:______
一、选择题(本大题共6小题,每小题3分,共18分.每小题只有一个正确选项)
1.下列图形中既是轴对称图形,又是中心对称图形的是
( C )
2.一元二次方程x2-2x+3=0根的情况是 ( C )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.无法判断
3.下列事件中属于必然事件的是 ( D )
A.一个图形经过旋转后所得的图形与原来的图形不一定全等
B.不等式的两边同时乘以一个数,结果仍是不等式
C.100件产品中有10件次品,从中任意抽取10件,有1件是次品
17
D.13名学生,至少有2名学生的生肖相同
4.抛物线y=ax2+bx+c(a≠0)过点(-1,0)和点(0,-3),且顶点在第四象限,设p=a+b+c,则p的取值范围是
( B )
A.-3<p<-1 B.-6<p<0
C.-3<p<0 D.-6<p<-3
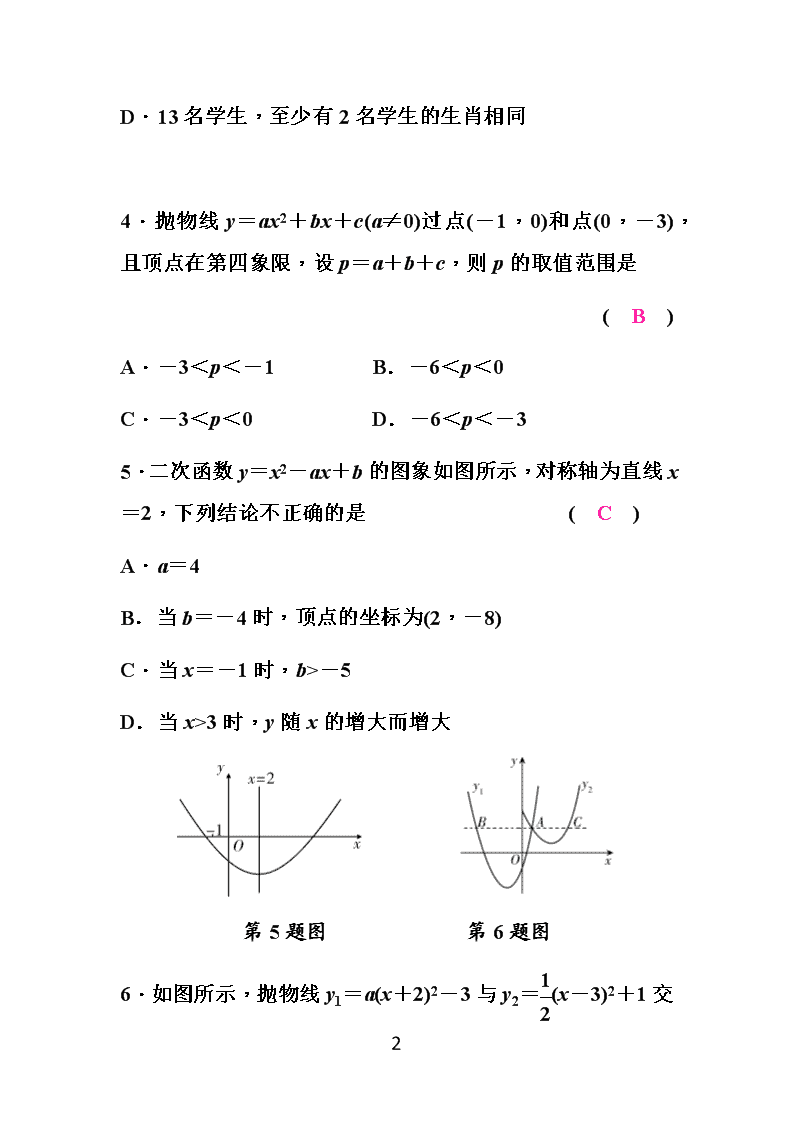
5.二次函数y=x2-ax+b的图象如图所示,对称轴为直线x=2,下列结论不正确的是 ( C )
A.a=4
B.当b=-4时,顶点的坐标为(2,-8)
C.当x=-1时,b>-5
D.当x>3时,y随x的增大而增大
第5题图 第6题图
6.如图所示,抛物线y1=a(x+2)2-3与y2=(x-3)2
17
+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C,则以下结论:①无论x取何值,y2的值总是正数;②a=1;③当x=0时,y2-y1=4;④2AB=3AC.其中正确结论是 ( D )
A.①② B.②③ C.③④ D.①④
二、填空题(本大题共6小题,每小题3分,共18分)
7.成语“守株待兔”所描述的事件是__随机__事件.
8.设x1,x2是方程x2-3x+2=0的两个根,则x1+x2-x1·x2=__1__.
9.△ABC的顶点坐标分别为A(4,4),B(1,5),C(-1,1),如果将△ABC绕C点逆时针旋转90°,得到△A′B′C,那么点A的对应点A′的坐标为 (-4,6) .
10.如图,把抛物线y=x2平移得到抛物线m.抛物线m经过点A(-6,0)和原点(0,0),它的顶点为P,它的对称轴与抛物线y=x2交于点Q,则图中阴影部分的面积为 13.5 .
第10题图 第11题图 第12题图
17
11.在如图所示的网格中,每个小正方形的边长都为2,若以小正方形的顶点为圆心,4为半径作一个扇形围成一个圆锥,则所围成的圆锥的底面圆的半径为____.
12.如图,在Rt△ABC中,∠C=90°,∠B=40°,点D在边BC上,BD=2CD,把△ABC绕点D逆时针旋转m°(0
0,∴m>-.
(2)由根与系数的关系得,x1+x2=-(2m+1),x1x2=m2-1,
∴原方程可化为(x1+x2)2-x1x2-17=0,
即(2m+1)2-(m2-1)-17=0,解得m1=,m2=-3,
∵m>-,∴m=.
16.某公司今年1月份的生产成本是400万元,由于改进了技术,生产成本逐月下降,3月份的生产成本是361万元.假设该公司2,3,4月每个月生产成本的下降率都相同.
(1)求每个月生产成本的下降率;
(2)请你预测4月份该公司的生产成本.
17
解:(1)设每个月生产成本的下降率为x,根据题意得
400(1-x)2=361,解得x1=0.05=5%,x2=1.95(不合题意,舍去).
答:每个月生产成本的下降率为5%.
(2)361×(1-5%)=342.95(万元).
答:预测4月份该公司的生产成本为342.95万元.
17.如图,在平面直角坐标系中,直角△ABC的三个顶点分别是(-3,1),B(0,3),C(0,1).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C1;
(2)分别连接AB1,BA1后,求四边形AB1A1B的面积.
解:(1)△A1B1C1如图所示;
17
(2)S四边形AB1A1B=·AA1·BB1
=× 6× 4=12.
四、(本大题共3小题,每小题8分,共24分)
18.元旦游园活动中,小文,小美,小红三位同学正在搬各自的椅子准备进行“抢凳子”游戏,看见李老师来了,小文立即邀请李老师参加,游戏规则如下:将三位同学的椅子背靠背放在教室中央,四人围着椅子绕圈行走,在行走过程中裁判员随机喊停,听到“停”后四人迅速抢坐在一张椅子上,没有抢坐到椅子的人淘汰,不能进入下一轮游戏.
(1)下列事件是必然事件的是 ( D )
A.李老师被淘汰
B.小文抢坐到自己带来的椅子
C.小红抢坐到小亮带来的椅子
D.有两位同学可以进入下一轮游戏
(2)如果李老师没有抢坐到任何一张椅子,三位同学都抢坐到了椅子但都没有抢坐到自己带来的椅子(记为事件A),
17
求出事件A的概率,请用树状图法或列表法加以说明.
解:设小文,小美,小红三位同学带来的椅子依次排列为a,b,c,画树状图如下:
由树状图可知,所有等可能结果共有6种,
其中第4种,第5种结果符合题意,
∴P(A)==.
19.如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD.
(1)求证:BD平分∠ABC;
(2)当∠ODB=30°时,求证:BC=OD.
17
证明:(1)∵AB为直径,∴BC⊥AC,
又OD⊥AC,∴OD∥BC,∴∠CBD=∠ODB,
又OB=OD,∠ODB=∠OBD,
∴∠CBD=∠OBD,∴BD平分∠ABC;
(2)∵OB=OD,∴∠OBD=∠ODB=30°,∴∠AOE=60°,
∴∠A=30°,又∠BCA=90°,∴BC=AB=OD.
20.如图,已知∠BAC=90°,△ABC绕点A逆时针旋转得到△ADE,恰好D在BC上,连接CE.
(1)∠BAE与∠DAC有何关系?并说明理由;
(2)线段BC与CE在位置上有何关系?为什么?
解:(1)∠BAE与∠DAC互补.理由:
∵△ABC绕点A逆时针旋转得到△ADE,
∴△ADE≌△ABC,
∴∠DAE=∠BAC=90°,
∴∠BAC+∠DAE=180°,
即∠BAD+∠DAC+∠DAC+∠CAE=180°,
17
∴∠BAE+∠DAC=180°.∴∠BAE与∠DAC互补.
(2)线段BC⊥CE.理由:∵∠CAE=∠BAD,∴∠ACE=.
又∵∠BCA=90°-∠ABD,∠ABD=,
∴∠BCA=90°-=.
∴∠ACE+∠BCA=+=90°,
即∠BCE=90°,∴BC⊥CE.
五、(本大题共2小题,每小题9分,共18分)
21.某商店经销一种学生用双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(个)与销售单价x(元)有如下关系:y=-x+60(30≤x≤60).设这种双肩包每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
17
(3)如果物价部门规定这种双肩包的销售单价不高于42元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?
解:(1)w=(x-30)·y=(x-30)·(-x+60)=-x2+90x-1 800,
∴w与x之间的函数关系式为w=-x2+90x-1 800(30≤x≤60).
(2)∵w=-x2+90x-1 800=-(x-45)2+225.
又-1<0,∴当x=45时,w有最大值,最大值为225.
答:当销售单价定为45元时,每天的销售利润最大,最大销售利润为225元.
(3)当w=200时,可得方程-(x-45)2+225=200.
解得x1=40,x2=50.
∵50>42,∴x2=50不符合题意,舍去.
∴销售单价定为40元.
答:该商店销售这种双肩包每天想要获得200元的销售利润,销售单价应定为40元.
22.如图,△ABD是⊙O的内接三角形,E是弦BD的中点,点C是⊙O外一点且∠DBC=∠A,连接OE
17
并延长与圆相交于点F,与BC相交于点C.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为6,BC=8,求弦BD的长.
(1)证明:连接OB,∵E是弦BD的中点,
∴BE=DE,OE⊥BD,==.
∴∠BOE=∠A,∠OBE+∠BOE=90°.
∵∠DBC=∠A,∴∠BOE=∠DBC.
∴∠OBE+∠DBC=90°.∴∠OBC=90°,
即BC⊥OB.∵OB为⊙O的半径,
∴BC是⊙O的切线.
(2)解:∵OB=6,BC=8,BC⊥OB,∴OC==10.
∵△OBC的面积为OC·BE=OB·BC,
∴BE===4.8,
17
∴BD=2BE=9.6,即弦BD的长为9.6.
六、(本大题共12分)
23.小贤与小杰在探究某类二次函数问题时,经历了如下过程:
求解体验:
(1)已知抛物线y=-x2+bx-3经过点(-1,0),则b=-4,顶点坐标为(-2,1),该抛物线关于点(0,1)成中心对称的抛物线的解析式是y=x2-4x+5;
抽象感悟:
我们定义:对于抛物线y=ax2+bx+c(a≠0),以y轴上的点M(0,m)为中心,作该抛物线关于点M中心对称的抛物线y′,则我们称抛物线y′为抛物线y的“衍生抛物线”,点M为“衍生中心”.
(2)已知抛物线y=-x2-2x+5关于点(0,m)中心对称的衍生抛物线为y′,若这两条抛物线有交点,求m的取值范围;
问题解决:
(3)已知抛物线y=ax2+2ax-b(a≠0).
17
①若抛物线y的衍生抛物线为y′=bx2-2bx+a2(b≠0),两抛物线有两个交点,且恰好是它们的顶点,求a,b的值及衍生中心的坐标;
②若抛物线y关于点(0,k+12)中心对称的衍生抛物线为y1,其顶点为A1;关于点(0,k+22)中心对称的衍生抛物线为y2,其顶点为A2;…;关于点(0,k+n2)中心对称的衍生抛物线为yn,其顶点为An…(n为正整数).求AnAn+1的长(用含n的式子表示).
解:求解体验:(1)∵抛物线y=-x2+bx-3经过点(-1,0),
∴-1-b-3=0,∴b=-4,
∴抛物线解析式为y=-x2-4x-3=-(x+2)2+1,
∴抛物线的顶点坐标为(-2,1),
∵抛物线的顶点坐标(-2,1)关于(0,1)的对称点为(2,1),
即新抛物线的顶点坐标为(2,1),令原抛物线的x=0,∴y=-3,
∴(0,-3)关于点(0,1)的对称点坐标为(0,5),
设新抛物线的解析式为y=a(x-2)2+1,
∵点(0,5)在新抛物线上,∴5=a(0-2)2+1,∴a=1,
17
∴新抛物线解析式为y=(x-2)2+1=x2-4x+5,
故答案为-4,(-2,1),y=x2-4x+5.
抽象感悟:(2)∵抛物线y=-x2-2x+5=-(x+1)2+6(Ⅰ),
∴抛物线的顶点坐标为(-1,6),设衍生抛物线为y′=a(x-1)2+2m-6,
∵抛物线y=-x2-2x+5关于点(0,m)中心对称的衍生抛物线为y′,∴a=1,∴衍生抛物线为y′=(x-1)2+2m-6=x2-2x+2m-5(Ⅱ),
联立(Ⅰ)(Ⅱ)得x2-2x+2m-5=-x2-2x+5,
整理得2x2=10-2m,∵这两条抛物线有交点,∴10-2m≥0,∴m≤5.
问题解决:(3)①抛物线y=ax2+2ax-b=a(x+1)2-a-b,
∴此抛物线的顶点坐标为(-1,-a-b),
∵抛物线y的衍生抛物线为y′=bx2-2bx+a2=b(x-1)2+a2-b,∴此衍生抛物线的顶点坐标为(1,a2-b),
∵两个抛物线有两个交点,且恰好是它们的顶点,
∴∴a=0(舍去)或a=3,∴b=-3,
17
∴抛物线y的顶点坐标为(-1,0),抛物线y的衍生抛物线的顶点坐标为(1,12),∴衍生中心的坐标为(0,6);
②抛物线y=ax2+2ax-b的顶点坐标为(-1,-a-b),
∵点(-1,-a-b)关于点(0,k+n2)的对称点为(1,a+b+2k+2n2),
∴抛物线yn的顶点坐标An为(1,a+b+2k+2n2),
同理An+1(1,a+b+2k+2(n+1)2),
∴AnAn+1=a+b+2k+2(n+1)2-(a+b+2k+2n2)=4n+2.
即AnAn+1的长为4n+2.
17