2021年中考数学压轴题专项训练 图形的相似（含解析）

2021年中考数学压轴题专项训练 图形的相似（含解析）

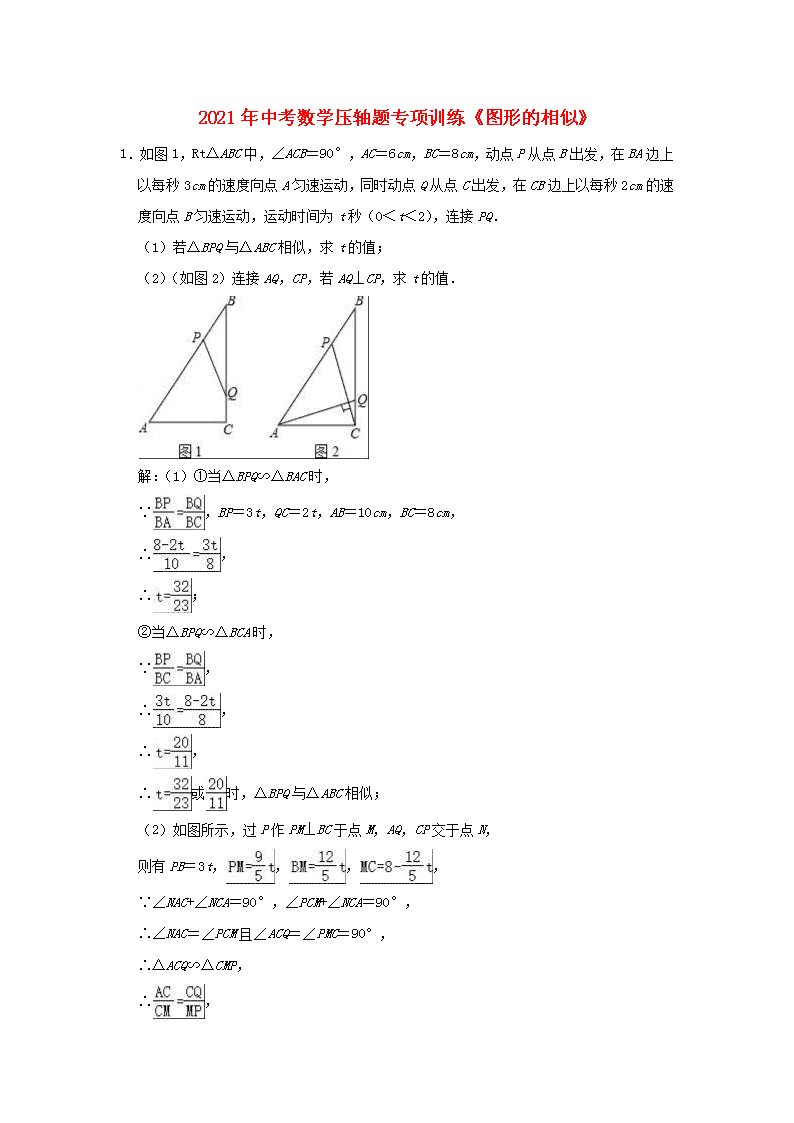
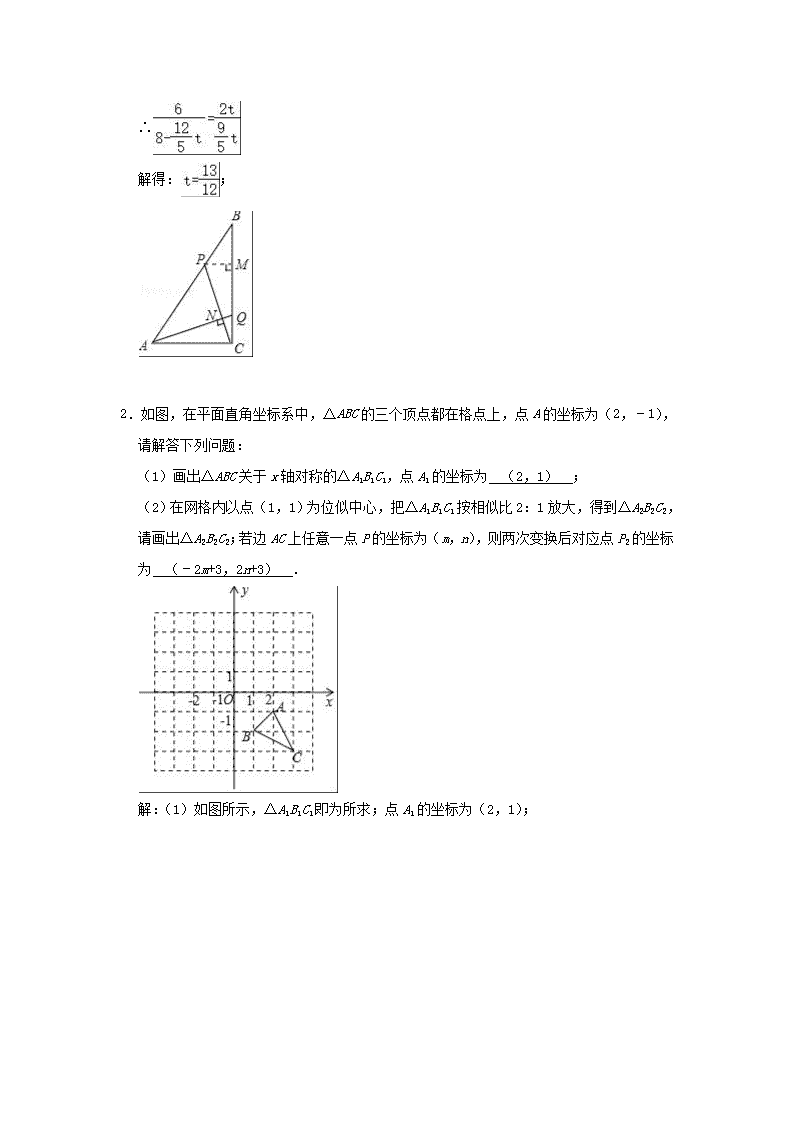
2021年中考数学压轴题专项训练《图形的相似》1．如图1，Rt△ABC中，∠ACB＝90°，AC＝6cm，BC＝8cm，动点P从点B出发，在BA边上以每秒3cm的速度向点A匀速运动，同时动点Q从点C出发，在CB边上以每秒2cm的速度向点B匀速运动，运动时间为t秒（0＜t＜2），连接PQ．（1）若△BPQ与△ABC相似，求t的值；（2）（如图2）连接AQ，CP，若AQ⊥CP，求t的值．解：（1）①当△BPQ∽△BAC时，∵，BP＝3t，QC＝2t，AB＝10cm，BC＝8cm，∴，∴；②当△BPQ∽△BCA时，∵，∴，∴，∴或时，△BPQ与△ABC相似；（2）如图所示，过P作PM⊥BC于点M，AQ，CP交于点N，则有PB＝3t，，，，∵∠NAC+∠NCA＝90°，∠PCM+∠NCA＝90°，∴∠NAC＝∠PCM且∠ACQ＝∠PMC＝90°，∴△ACQ∽△CMP，∴， ∴解得：；2．如图，在平面直角坐标系中，△ABC的三个顶点都在格点上，点A的坐标为（2，﹣1），请解答下列问题：（1）画出△ABC关于x轴对称的△A1B1C1，点A1的坐标为　（2，1）　；（2）在网格内以点（1，1）为位似中心，把△A1B1C1按相似比2：1放大，得到△A2B2C2，请画出△A2B2C2；若边AC上任意一点P的坐标为（m，n），则两次变换后对应点P2的坐标为　（﹣2m+3，2n+3）　．解：（1）如图所示，△A1B1C1即为所求；点A1的坐标为（2，1）； 故答案为：（2，1）；（2）如图所示，△A2B2C2即为所求；P2的坐标为（﹣2m+3，2n+3）．故答案为：（﹣2m+3，2n+3）．3．综合与实践﹣探究正方形旋转中的数学问题问题情境：已知正方形ABCD中，点O在BC边上，且OB＝2OC．将正方形ABCD绕点O顺时针旋转得到正方形A′B′C′D′（点A′，B′，C′，D′分别是点A，B，C，D的对应点）．同学们通过小组合作，提出下列数学问题，请你解答．特例分析：（1）“乐思”小组提出问题：如图1，当点B′落在正方形ABCD的对角线BD上时，设线段A′B′与CD交于点M．求证：四边形OB′MC是矩形；（2）“善学”小组提出问题：如图2，当线段A′D′经过点D时，猜想线段C′O与D′D满足的数量关系，并说明理由；深入探究：（3）请从下面A，B两题中任选一题作答．我选择　A　题．A．在图2中连接AA′和BB′，请直接写出的值．B．“好问”小组提出问题：如图3，在正方形ABCD绕点O顺时针旋转的过程中，设直线BB′交线段AA′于点P．连接OP，并过点O作OQ⊥BB′于点Q．请在图3中补全图形，并直接写出的值． （1）证明：∵四边形ABCD是正方形，∴BC＝CD，∠C＝90°，∴∠CBD＝∠CDB＝45°；由旋转可知，OB＝OB’，∴∠OB’B＝∠OBB’＝45°，∵∠B’OC是△BOB’的一个外角，∴∠B’OC＝∠OB’B+∠OBB’＝45°+45°＝90°，∵四边形A’B’C’D’是正方形，∴∠OB’M＝90°，∴四边形OB’MC是矩形；（2）解：D’D＝2C’O，理由如下：如图2①，连接OD，OD’，过点O作OE⊥D’D于点E，则∠OED’＝90°，由旋转可知，OD＝OD’，则D’D＝2D’E，∵四边形A’B’C’D’是正方形，∴∠C′＝∠OED′＝90°，∴四边形OC’D’E是矩形，∴C’O＝D’E，∴D’D＝2C’O；（3）解：A、如图2②，连接AA′，BB′，OA，OA′，∵将正方形ABCD绕点O顺时针旋转得到正方形A′B′C′D′，∴OB＝OB′，OA＝OA′，∠BOB′＝∠AOA′，∴，∴△OBB′∽△OAA′， ∴＝，∵AB＝BC，OB＝2OC，∴设OC＝x，则OB＝2x，∴AB＝BC＝3x，∴OA＝＝＝x，∴＝＝＝；B、如图3，连接OA，OA′，∵将正方形ABCD绕点O顺时针旋转得到正方形A′B′C′D′，∴OB＝OB′，OA＝OA′，∠BOB′＝∠AOA′，∴∠OBB′＝∠OAA′，∴点A，B，O，P四点共圆，∴∠ABO+∠APO＝180°，∴∠APO＝90°，∵OQ⊥BB′，∴∠BQO＝∠APO＝90°，∴△OAP∽△OBQ，∴＝． 4．如图，矩形OABC边OA，OC分别在x轴，y轴上，且OA＝8，OC＝6，连接OB，点D为OB中点，点E从点A出发以每秒1个单位长度运动到点B停止，设运动时间为t（0＜t＜6），连接DE，作DF⊥DE交OA于F，连接EF．（1）如图1，当四边形DFAE为矩形时，求t的值；（2）如图2，试证明在运动过程中，△DFE∽△ABO；（3）当t为何值时，△AEF面积最大？最大值为多少？解：（1）∵四边形OABC是矩形，∴AB＝OC＝6，∠OAB＝90°，∵四边形DFAE是矩形，∴∠BED＝90°＝∠OAB，∴DE∥OA，∵点D是OB的中点， ∴点E是AB中点，∴AE＝AB＝3，由运动知，AE＝t，∴t＝3；（2）如图2所示：作DM⊥OA于M，DN⊥AB于N，∵四边形OABC是矩形，∴OA⊥AB，∴四边形DMAN是矩形，∴∠MDN＝90°，DM∥AB，DN∥OA，∴＝，＝，∵点D为OB的中点，∴M、N分别是OA、AB的中点，∴DM＝AB＝3，DN＝OA＝4，∵∠EDF＝90°，∴∠FDM＝∠EDN，又∵∠DMF＝∠DNE＝90°，∴△DMF∽△DNE，∴＝＝，∵OA＝8，AB＝6， ∴，∴，∵∠FDE＝∠BAO＝90°，∴△DFE∽△ABO；（3）如图2，由（2）知，△DMF∽△DNE，∴，由运动知，AE＝t，当0＜t≤3时，NE＝3﹣t，∴，∴MF＝（3﹣t），∴AF＝AM+MF＝4+（3﹣t）＝8﹣t当3＜t＜6时，NE＝t﹣3，∴∴MF＝（t﹣3），∴AF＝AM﹣MF＝4﹣（t﹣3）＝8﹣t，∴S△AEF＝AE×AF＝•t（8﹣t）＝﹣（t﹣3）2+6，当t＝3时，△AEF面积最大，最大值为6．5．如图，∠MBN＝45°，点P为∠MBN内的一个动点，过点P作∠BPA与∠BPC，使得∠BPA＝∠BPC＝135°，分别交BM、BN于点A、C．（1）求证：△CPB∽△BPA；（2）连接AC，若AC⊥BC，试求的值；（3）记AP＝a，BP＝b，CP＝c，若a+b﹣c＝20，a≥2b，且a、b、c为整数，求a，b，c的值．（1）证明：∵∠BPA＝135°， ∴∠ABP+∠BAP＝180°﹣135°＝45°，∵∠ABP+∠CBP＝∠MBN＝45°，∴∠ABP+∠BAP＝∠ABP+∠CBP，∴∠BAP＝∠CBP，∵∠BPA＝∠BPC，∴△CPB∽△BPA；（2）解：∵AC⊥BC，∠MBN＝45°，∴△ACB是等腰直角三角形，∴AB＝BC，∵△CPB∽△BPA，∴＝＝＝＝，设PC＝a，则BP＝a，AP＝2a，∵∠APC＝360°﹣135°﹣135°＝90°，∴AC＝＝＝a，∴＝＝；（3）解：∵△CPB∽△BPA，∴＝，即＝≥2，∴c≤，∴a+b﹣c≥2b+b﹣＝b，∴b≤20，∴b≤8，∵a、b、c为整数，∴当b＝8时，a＝16，c＝4；当b＝7时，a＝14，c＝1；当b＜7时，c＜0（不合题意舍去）， ∴a，b，c的值分别为16，8，4或14，7，1．6．如图，Rt△ABC中，∠BAC＝90°，AB＝2，AC＝4，D是BC边上一点，且BD＝CD，G是BC边上的一动点，GE∥AD分别交直线AC，AB于F，E两点．（1）AD＝　　；（2）如图1，当GF＝1时，求的值；（3）如图2，随点C位置的改变，FG+EG是否为一个定值？如果是，求出这个定值，如果不是，请说明理由．解：（1）∵∠BAC＝90°，且BD＝CD，∴AD＝BC，∵BC＝＝＝2，∴AD＝×2＝，故答案为：；（2）如图1，∵GF∥AD，∴∠CFG＝∠CAD，∵BD＝CD＝BC＝AD＝，∴∠CAD＝∠C，∴∠CFG＝∠C，∴CG＝FG＝1，∴BG＝2﹣1，∵AD∥GE，∴△BGE∽△BDA，∴＝＝＝； （3）如图2，随点C位置的改变，FG+EG是一个定值，理由如下：∵AD＝BC＝BD，∴∠B＝∠BAD，∵AD∥EG，∴∠BAD＝∠E，∴∠B＝∠E，∴EG＝BG，由（2）知，GF＝GC，∴EG+FG＝BG+CG＝BC＝2，∴FG+EG是一个定值，为2．7．△ABC中，∠C＝90°，∠A＝60°，AC＝2cm．长为1cm的线段MN在△ABC的边AB上沿AB方向以1cm/s的速度向点B运动（运动前点M与点A重合）．过M，N分别作AB的垂线交直角边于P，Q两点，线段MN运动的时间为ts．（1）当0≤t≤1时，PM＝　tcm　，QN＝　（3﹣t）cm　（用t的代数式表示）；（2）线段MN运动过程中，四边形MNQP有可能成为矩形吗？若有可能，求出此时t的值；若不可能，说明理由；（3）t为何值时，以C，P，Q为顶点的三角形与△ABC相似？ 解：（1）由题意得：AM＝t，∵PM⊥AB，∴∠PMA＝90°，∵∠A＝60°，∴∠APM＝30°，∴PM＝AM＝t．∵∠C＝90°，∴∠B＝90°﹣∠A＝30°，∴AB＝2AC＝4，BC＝AC＝2，∵MN＝1，∴BN＝AM﹣AM﹣1＝3﹣t，∵QN⊥AB，∴QN＝BN＝（3﹣t）；故答案为：tcm，（3﹣t）cm．（2）四边形MNQP有可能成为矩形，理由如下：由（1）得：QN＝（3﹣t）．由条件知，若四边形MNQP为矩形，则需PM＝QN，即t＝（3﹣t），∴t＝．∴当t＝s时，四边形MNQP为矩形；（3）由（2）知，当t＝s时，四边形MNQP为矩形，此时PQ∥AB，∴△PQC∽△ABC．除此之外，当∠CPQ＝∠B＝30°时，△QPC∽△ABC， 此时＝tan30°＝．∵＝cos60°＝，∴AP＝2AM＝2t．∴CP＝2﹣2t．∵＝cos30°＝，∴BQ＝（3﹣t）．又∵BC＝2，∴CQ＝2．∴．综上所述，当s或s时，以C，P，Q为顶点的三角形与△ABC相似．8．如图1，在Rt△ABC中，∠BAC＝90°，AB＝AC，D，E两点分别在AC，BC上，且DE∥AB，将△CDE绕点C按顺时针方向旋转，记旋转角为α．（1）问题发现：当α＝0°时，的值为　　；（2）拓展探究：当0°≤α＜360°时，若△EDC旋转到如图2的情况时，求出的值；（3）问题解决：当△EDC旋转至A，B，E三点共线时，若设CE＝5，AC＝4，直接写出线段BE的长　7或1　．解：（1）∵∠BAC＝90°，AB＝AC，∴△ABC为等腰直角三角形，∠B＝45°，∵DE∥AB，∴∠DEC＝∠B＝45°，∠CDE＝∠A＝90°，∴△DEC为等腰直角三角形， ∴cos∠C＝＝，∵DE∥AB，∴＝＝，故答案为：；（2）由（1）知，△BAC和△CDE均为等腰直角三角形，∴＝＝，又∠BCE＝∠ACD＝α，∴△BCE∽△ACD，∴＝＝，即＝；（3）①如图3﹣1，当点E在线段BA的延长线上时，∵∠BAC＝90°，∴∠CAE＝90°，∴AE＝＝＝3，∴BE＝BA+AE＝4+3＝7；②如图3﹣2，当点E在线段BA上时，AE＝＝＝3，∴BE＝BA﹣AE＝4﹣3＝1，综上所述，BE的长为7或1，故答案为：7或1． 9．如图，在正方形ABCD中，E为AB边上一点，连接DE，交AC于H点，过点D作DF⊥DE，交BC的延长线于F，连接EF交于AC于点G．（1）请写出AE和CF的数量关系：　相等　；（2）求证：点G是EF的中点；（3）若正方形ABCD的边长为4，且AE＝1，求GH•GA的值．解：（1）∵四边形ABCD是正方形，∴∠ADC＝∠EAD＝∠DCB＝∠DCF＝90°，AD＝DC，∵DF⊥DE，∴∠EDF＝90°，∴∠ADE+∠EDC＝∠EDC+∠CDF，∴∠ADE＝∠CDF，∴△ADE≌△CDF（ASA）， ∴AE＝CF，故答案为：相等；（2）如右图，过E作EM∥BC交AC于M，∵四边形ABCD是正方形，AC为对角线，∴，∵EM∥BC，∴∠AEM＝∠B＝90°，∴∠AME＝90°﹣∠EAM＝45°，∴∠AEM＝∠EAM，∴AE＝EM，∵AE＝CF，∴EM＝CF，∵EM∥BC，∴∠MEG＝∠GFC，∠EMG＝∠GCF，∴△EMG≌△FCG（ASA），∴EG＝FG，∴G为EF的中点；（3）由（1）知△DAE≌△DCF，∴DE＝DF，∴∠DEF＝∠DFE，∵∠DEF＝90°，∴∠DEF＝45°，∵∠BAC＝45°，∴∠DEF＝∠BAC，∵∠AGE＝∠AGE，∴△GEH∽△GAE，∴＝， ∴EG2＝GH•AG，∵AE＝1，则CF＝1，BF＝5，∴EF＝＝＝，∴．10．如图，△ABC和△DEF是两个全等的等腰直角三角形，∠BAC＝∠EDF＝90°，△DEF的顶点E与△ABC的斜边BC的中点重合，将△DEF绕点E旋转，旋转过程中，线段DE与线段AB相交于点P，线段EF与射线CA相交于点Q．（1）当点Q在线段CA上时，如图1，求证：△BPE∽△CEQ．（2）当点Q在线段CA的延长线上时，如图2，△BPE和△CEQ是否相似？说明理由；若BP＝1，CQ＝，求PQ的长．（1）证明：∵△ABC和△DEF是两个全等的等腰直角三角形，∴∠B＝∠C＝∠DEF＝45°，∵∠BEQ＝∠EQC+∠C，即∠BEP+∠DEF＝∠EQC+∠C，∴∠BEP+45°＝∠EQC+45°，∴∠BEP＝∠EQC，∵∠B＝∠C， ∴△BPE∽△CEQ；（2）△BPE∽△CEQ；理由如下：∵∠BEQ＝∠EQC+∠C，即∠BEP+∠DEF＝∠EQC+∠C，∴∠BEP+45°＝∠EQC+45°，∴∠BEP＝∠EQC，又∵∠B＝∠C，∴△BPE∽△CEQ；∴＝，∵△DEF的顶点E与△ABC的斜边BC的中点重合，∴BE＝CE，∴＝，解得：BE＝CE＝，∴BC＝3，在Rt△ABC中，AB＝AC，∴AB＝AC＝BC＝×3＝3，∴AQ＝CQ﹣AC＝﹣3＝，AP＝AB﹣BP＝3﹣1＝2，在Rt△APQ中，PQ＝＝＝．11．已知：在△EFG中，∠EFG＝90°，EF＝FG，且点E，F分别在矩形ABCD的边AB，AD上．（1）如图1，当点G在CD上时，求证：△AEF≌△DFG；（2）如图2，若F是AD的中点，FG与CD相交于点N，连接EN，求证：EN＝AE+DN；（3）如图3，若AE＝AD，EG，FG分别交CD于点M，N，求证：MG2＝MN•MD 解：（1）∵四边形ABCD是矩形，∴∠A＝∠D＝90°，∴∠AEF+∠AFE＝90°，∵∠EFG＝90°，∴∠AFE+∠DFG＝90°，∴∠AEF＝∠DFG，∵EF＝FG，∴△AEF≌△DFG（AAS）；（2）如图2，，延长NF，EA相交于H，∴∠AFH＝∠DFN，由（1）知，∠EAF＝∠D＝90°，∴∠HAF＝∠D＝90°，∵点F是AD的中点，∴AF＝DF，∴△AHF≌△DNF（ASA），∴AH＝DN，FH＝FN，∵∠EFN＝90°，∴EH＝EN，∵EH＝AE+AH＝AE+DN，∴EN＝AE+DN；（3）如图3， 过点G作GP⊥AD交AD的延长线于P，∴∠P＝90°，同（1）的方法得，△AEF≌△PFG（AAS），∴AF＝PG，PF＝AE，∵AE＝AD，∴PF＝AD，∴AF＝PD，∴PG＝PD，∵∠P＝90°，∴∠PDG＝45°，∴∠MDG＝45°，在Rt△EFG中，EF＝FG，∴∠FGE＝45°，∴∠FGE＝∠GDM，∵∠GMN＝∠DMG，∴△MGN∽△MDG，∴，MG2＝MN•MD． 12．在△ABC中，∠ACB＝90°，AB＝20，BC＝12．（1）如图1，折叠△ABC使点A落在AC边上的点D处，折痕交AC、AB分别于Q、H，若S△ABC＝9S△DHQ，则HQ＝　4　．（2）如图2，折叠△ABC使点A落在BC边上的点M处，折痕交AC、AB分别于E、F．若FM∥AC，求证：四边形AEMF是菱形；（3）在（1）（2）的条件下，线段CQ上是否存在点P，使得△CMP和△HQP相似？若存在，求出PQ的长；若不存在，请说明理由．解：（1）如图1中，在△ABC中，∵∠ACB＝90°，AB＝20，BC＝12，∴AC＝＝16，设HQ＝x， ∵HQ∥BC，∴＝，∴，∴AQ＝x，∵S△ABC＝9S△DHQ，∴×16×12＝9××x×x，∴x＝4或﹣4（舍弃），∴HQ＝4，故答案为4．（2）如图2中，由翻折不变性可知：AE＝EM，AF＝FM，∠AFE＝∠MFE，∵FM∥AC，∴∠AEF＝∠MFE，∴∠AEF＝∠AFE，∴AE＝AF，∴AE＝AF＝MF＝ME，∴四边形AEMF是菱形．（3）如图3中， 设AE＝EM＝FM＝AF＝4m，则BM＝3m，FB＝5m，∴4m+5m＝20，∴m＝，∴AE＝EM＝，∴EC＝AC﹣AE＝16﹣＝，∴CM＝＝，∵QH＝4，AQ＝，∴QC＝，设PQ＝x，当＝时，△HQP∽△MCP，∴，解得：x＝，当＝时，△HQP∽△PCM，∴解得：x＝8或，经检验：x＝10或是分式方程的解，且符合题意，综上所述，满足条件长QP的值为或8或．13．如图，在△ABC中，AB＝AC＝10，BC＝16，点D为BC边上的一个动点（点D不与点B、点C重合）．以D为顶点作∠ADE＝∠B，射线DE交AC边于点E，过点A作AF⊥AD交射线 DE于点F．（1）求证：AB•CE＝BD•CD；（2）当DF平分∠ADC时，求AE的长；（3）当△AEF是等腰三角形时，求BD的长．（1）证明：∵AB＝AC，∴∠B＝∠C，∠ADC＝∠BAD+∠B，∠ADE＝∠B，∴∠BAD＝∠CDE，又∠B＝∠C，∴△BAD∽△CDE，∴＝，即AB•CE＝BD•CD；（2）解：∵DF平分∠ADC，∴∠ADE＝∠CDE，∵∠CDE＝∠BAD，∴∠ADE＝∠BAD，∴DF∥AB，∴＝，∵∠BAD＝∠ADE＝∠B，∴∠BAD＝∠C，又∠B＝∠B，∴△BDA∽△BAC，∴＝，即＝解得，BD＝，∴＝， 解得，AE＝；（3）解：作AH⊥BC于H，∵AB＝AC，AH⊥BC，∴BH＝HC＝BC＝8，由勾股定理得，AH＝＝＝6，∴tanB＝＝，∴tan∠ADF＝＝，设AF＝3x，则AD＝4x，由勾股定理得，DF＝＝5x，∵△BAD∽△CDE，∴＝，当点F在DE的延长线上，FA＝FE时，DE＝5x﹣3x＝2x，∴＝，解得，CD＝5，∴BD＝BC﹣CD＝11，当EA＝EF时，DE＝EF＝2.5x，∴＝，解得，CD＝，∴BD＝BC﹣CD＝；当AE＝AF＝3x时，DE＝x，∴＝，解得，CD＝，∴BD＝BC﹣CD＝；当点F在线段DE上时，∠AFE为钝角， ∴只有FA＝FE＝3x，则DE＝8x，∴＝，解得，CD＝20＞16，不合题意，∴△AEF是等腰三角形时，BD的长为11或或．14．如图，已知平行四边形ABCD中，AD＝，AB＝5，tanA＝2，点E在射线AD上，过点E作EF⊥AD，垂足为点E，交射线AB于点F，交射线CB于点G，联结CE、CF，设AE＝m．（1）当点E在边AD上时，①求△CEF的面积；（用含m的代数式表示）②当S△DCE＝4S△BFG时，求AE：ED的值；（2）当点E在边AD的延长线上时，如果△AEF与△CFG相似，求m的值．解：（1）①∵EF⊥AD，∴∠AEF＝90°，在Rt△AEF中，tanA＝2，AE＝m，∴EF＝AEtanA＝2m，根据勾股定理得，AF＝＝m，∵AB＝5，∴BF＝5﹣m，∵四边形ABCD是平行四边形，∴BC＝AD＝，AD∥BC，∴∠G＝∠AEF＝90°， ∴△AEF∽△BGF，∴，∴，∴BG＝﹣m，∴CG＝BC+BG＝+﹣m＝2﹣m，∴S△CEF＝EF•CG＝•2m•（2﹣m）＝2m﹣m2；②由①知，△AEF∽△BGF，∴，∴FG＝•EF＝•2m＝2（﹣m），∴EG＝EF+FG＝2m+2（﹣m）＝2，∴S△CDE＝DE•EG＝（﹣m）•2＝5﹣m，S△BFG＝BG•FG＝（﹣m）•2（﹣m）＝（﹣m）2，S△DCE＝4S△BFG时，∴5﹣m＝4（﹣m）2，∴m＝（舍）或m＝，∴DE＝AD﹣AE＝﹣＝，∴AE：ED＝：＝3，即：AE：ED的值为3；（2）∵四边形ABCD是平行四边形，∴BC＝AD＝，AD∥BC，∵EF⊥AD，∴EF⊥BC，∴∠AEF＝∠CGF＝90°，∵△AEF与△CFG相似， ∴①当△AEF∽△CGF时，如图1，∴∠AFE＝∠CFG，∵EF⊥BC，∴BG＝BC＝，∵AD∥BC，∴∠CBF＝∠A，∵tanA＝2，∴tan∠CBF＝2，在Rt△BGF中，FG＝BGtan∠CBF＝，根据勾股定理得，BF＝＝，∴AF＝AB+BF＝5+＝，∵BC∥AD，∴△BGF∽△AEF，∴，∴，∴m＝；②当△AEF∽△CGF时，如图2，∴∠EAF＝∠GFC，∵∠EAF+∠AFE＝90°，∴∠GFC+∠AFE＝90°，∴∠AFC＝90°，∵AD∥BC，∴∠CBF＝∠A，∴tan∠CBF＝tanA＝2，在R△BFC中，CF＝BF•∠CBF＝2BF，根据勾股定理得，BF2+CF2＝BC2， ∴BF2+4BF2＝（）2，∴BF＝1，∴AF＝AB+BF＝6，在Rt△BGF中，同理：BG＝，∵AD∥BC，∴△BGF∽△AEF，∴，∴，∴m＝．即：如果△AEF与△CFG相似，m的值为或．15．如图，在平面直角坐标系中，过原点O及A（8，0）、C（0，6）作矩形OABC，连接AC，一块直角三角形PDE的直角顶点P始终在对角线AC上运动（不与A、C重合），且保持一边PD始终经过矩形点B，PE交x轴于点Q（1）＝　　；（2）在点P从点C运动到点A的过程中，的值是否发生变化？如果变化，请求出其变化范围，如果不变，请说明理由，并求出其值；（3）若将△QAB沿直线BQ折叠后，点A与点P重合，则PC的长为　2.8　． 解：（1）∵A（8，0）、C（0，6），∴OA＝8，OC＝6，∵四边形OABC是矩形，∴∠ABC＝∠OAB＝90°，BC＝OA＝8，AB＝OC＝6，∴＝＝，故答案为：；（2）的值不发生变化，＝，理由如下：∵∠OAB＝∠BPQ＝90°，∴∠AOB+∠BPQ＝180°，∴A、B、P、Q四点共圆，∴∠PQB＝∠PAB，∵∠ABC＝∠BPQ＝90°，∴△PBQ∽△BCA，∴＝＝；（3）设BQ交AP于M，如图所示：在Rt△ABC中，由勾股定理得：AC＝＝＝10，由折叠的性质得：BQ⊥AP，PM＝AM，∴∠AMB＝90°＝∠ABC，∵∠BAM＝∠CAB，∴△ABM∽△ACB，∴＝，即＝， 解得：AM＝3.6，∴PA＝2AM＝7.2，∴PC＝AC﹣PA＝10﹣7.2＝2.8；故答案为：2.8．