中考数学规律探索题(中考找规律题目)+中考数学函数复习专题大全集
中考数学规律探索题(中考找规律题目)+中考数学函数复习专题大全集中考规律探索:以下为全部整理类型,规律探索共两套试题一.选择题1.观察下列等式:31=3,32=9,33=27,34=81,35=243,36=729,37=2187…解答下列问题:3+32+33+34…+32013的末位数字是( )A.0B.1C.3D.72.把所有正奇数从小到大排列,并按如下规律分组:(1),(3,5,7),(9,11,13,15,17),(19,21,23,25,27,29,31),…,现用等式AM=(i,j)表示正奇数M是第i组第j个数(从左往右数),如A7=(2,3),则A2013=()A.(45,77)B.(45,39)C.(32,46)D.(32,23)3.下表中的数字是按一定规律填写的,表中a的值应是.1235813a…2358132134…4.下列图形都是由同样大小的矩形按一定的规律组成,其中第(1)个图形的面积为2cm2,第(2)个图形的面积为8cm2,第(3)个图形的面积为18cm2,……,第(10)个图形的面积为()A.196cm2B.200cm2C.216cm2D.256cm25.如图,动点P从(0,3)出发,沿所示的方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第2013次碰到矩形的边时,点P的坐标为()A、(1,4)B、(5,0)C、(6,4)D、(8,3)6.如图,下列各图形中的三个数之间均具有相同的规律.根据此规律,图形中M与m、n的关系是A.M=mnB.M=n(m+1)C.M=mn+1D.M=m(n+1)
7.我们知道,一元二次方程没有实数根,即不存在一个实数的平方等于-1,若我们规定一个新数“”,使其满足(即方程有一个根为),并且进一步规定:一切实数可以与新数进行四则运算,且原有的运算律和运算法则仍然成立,于是有,从而对任意正整数n,我们可得到同理可得那么,的值为A.0 B.1 C.-1 D.8.下列图形都是由同样大小的棋子按一定的规律组成,其中第①个图形有1颗棋子,第②个图形一共有6颗棋子,第③个图形一共有16颗棋子,…,则第⑥个图形中棋子的颗数为()图①图②图③···(第8题图)A.51B.70C.76D.81二.填空题1.观察下列图形中点的个数,若按其规律再画下去,可以得到第n个图形中所有的个数为(用含n的代数式表示).2.如图,在直角坐标系中,已知点A(﹣3,0)、B(0,4),对△OAB连续作旋转变换,依次得到△1、△2、△3、△4…,则△2013的直角顶点的坐标为.3.如图,正方形ABCD的边长为1,顺次连接正方形ABCD四边的中点得到第一个正方形A1B1C1D1,由顺次连接正方形A1B1C1D1四边的中点得到第二个正方形A2B2C2D2…,以此类推,则第六个正方形A6B6C6D6周长是 .
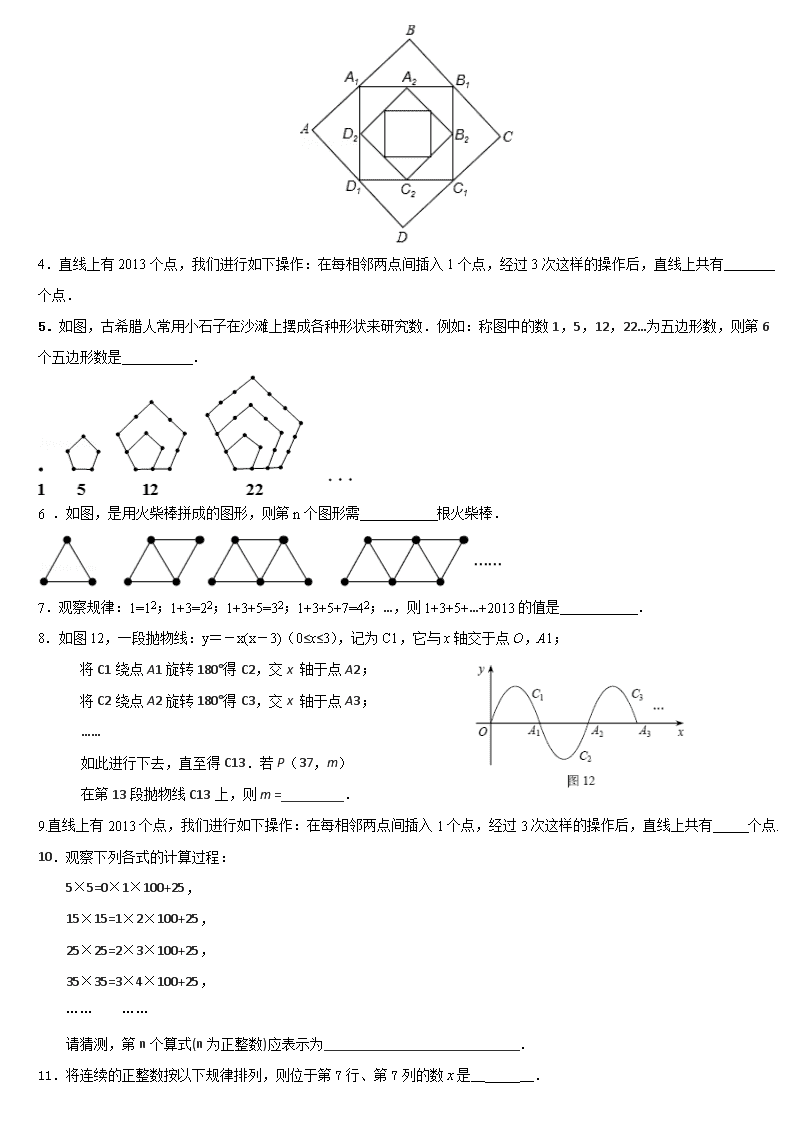
4.直线上有2013个点,我们进行如下操作:在每相邻两点间插入1个点,经过3次这样的操作后,直线上共有个点.5.如图,古希腊人常用小石子在沙滩上摆成各种形状来研究数.例如:称图中的数1,5,12,22…为五边形数,则第6个五边形数是 .6.如图,是用火柴棒拼成的图形,则第n个图形需 根火柴棒.7.观察规律:1=12;1+3=22;1+3+5=32;1+3+5+7=42;…,则1+3+5+…+2013的值是 .8.如图12,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;……如此进行下去,直至得C13.若P(37,m)在第13段抛物线C13上,则m=_________.9.直线上有2013个点,我们进行如下操作:在每相邻两点间插入1个点,经过3次这样的操作后,直线上共有个点.10.观察下列各式的计算过程:5×5=0×1×100+25,15×15=1×2×100+25,25×25=2×3×100+25,35×35=3×4×100+25,…………请猜测,第n个算式(n为正整数)应表示为____________________________.11.将连续的正整数按以下规律排列,则位于第7行、第7列的数是____.
12、如下图,每一幅图中均含有若干个正方形,第①幅图中含有1个正方形;第②幅图中含有5个正方形;……按这样的规律下去,则第(6)幅图中含有个正方形;①②③13.将一些半径相同的小圆按如图所示的规律摆放:第1个图形有6个小圆,第2个图形有10个小圆,第3个图形有16个小圆,第4个图形有24个小圆,……,依次规律,第6个图形有 个小圆.14.已知一组数2,4,8,16,32,…,按此规律,则第n个数是 .15、我们知道,经过原点的抛物线的解析式可以是y=ax2+bx(a≠0)(1)对于这样的抛物线:当顶点坐标为(1,1)时,=__________;当顶点坐标为(m,m),m≠0时,与m之间的关系式是__________;(2)继续探究,如果b≠0,且过原点的抛物线顶点在直线y=kx(k≠0)上,请用含的代数式表示b;(3)现有一组过原点的抛物线,顶点A1,A2,…,An在直线y=x上,横坐标依次为1,2,…,n(为正整数,且n≤12),分别过每个顶点作轴的垂线,垂足记为B1,B2,…,Bn,以线段AnBn为边向右作正方形AnBnCnDn,若这组抛物线中有一条经过Dn,求所有满足条件的正方形边长.16.如图,所有正三角形的一边平行于x轴,一顶点在y轴上,从内到外,它们的边长依次为2,4,6,8,…,顶点依次用、、、、…表示,其中与x轴、底边与、与、…均相距一个单位,则顶点的坐标是,的坐标是.
第16题图17.如图,已知直线l:y=x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;……按此作法继续下去,则点A2013的坐标为.18、如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…那么点A4n+1(n为自然数)的坐标为(用n表示)19.当白色小正方形个数等于1,2,3…时,由白色小正方形和和黑色小正方形组成的图形分别如图所示.则第个图形中白色小正方形和黑色小正方形的个数总和等于_____________.(用表示,是正整数)20.(2013•衢州4分)如图,在菱形ABCD中,边长为10,∠A=60°.顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去….则四边形A2B2C2D2的周长是 ;四边形A2013B2013C2013D2013的周长是 .
21.一组按规律排列的式子:a2,,,,….则第n个式子是________22.观察下面的单项式:a,﹣2a2,4a3,﹣8a4,…根据你发现的规律,第8个式子是 .23.如图,已知直线l:y=x,过点M(2,0)作x轴的垂线交直线l于点N,过点N作直线l的垂线交x轴于点M1;过点M1作x轴的垂线交直线l于N1,过点N1作直线l的垂线交x轴于点M2,…;按此作法继续下去,则点M10的坐标为 .24.为庆祝“六•一”儿童节,某幼儿园举行用火柴棒摆“金鱼”比赛.如图所示:按照上面的规律,摆第(n)图,需用火柴棒的根数为 .
答案:选择题:1、C2、C3、214、B5、D6、D7、D8、C填空题:1、(n+1)22、(8052,0)3、0.54、160975、516、2n+17、10140498、29、1609710、[10(n-1)+5]2=100n(n-1)+2511、8512、9113、4614、2n15、(1)-1;a=-(或am+1=0);(2)解:∵a≠0∴y=ax2+bx=a(x+)2-∴顶点坐标为(-,-)∵顶点在直线y=kx上∴k(-)=-∵b≠0∴b=2k(3)解:∵顶点An在直线y=x上∴可设An的坐标为(n,n),点Dn所在的抛物线顶点坐标为(t,t)由(1)(2)可得,点Dn所在的抛物线解析式为y=-x2+2x∵四边形AnBnCnDn是正方形∴点Dn的坐标为(2n,n)∴-(2n)2+2×2n=n∴4n=3t∵t、n是正整数,且t≤12,n≤12∴n=3,6或9∴满足条件的正方形边长为3,6或9[中国教*育&#^@出版网]
16、(0,),(-8,-8).17、(注:以上两答案任选一个都对)18、(2n,1)19、n2+4n20、20;21、(n为正整数)22、-128a823、(884736,0)24、6n+2
规律探索21、我们平常用的数是十进制数,如2639=2×103+6×102+3×101+9×100,表示十进制的数要用10个数码(又叫数字):0,1,2,3,4,5,6,7,8,9。在电子数字计算机中用的是二进制,只要两个数码:0和1。如二进制中101=1×22+0×21+1×20等于十进制的数5,10111=1×24+0×23+1×22+1×21+1×20等于十进制中的数23,那么二进制中的1101等于十进制的数。2、从1开始,将连续的奇数相加,和的情况有如下规律:1=1=12;1+3=4=22;1+3+5=9=32;1+3+5+7=16=42;1+3+5+7+9=25=52;…按此规律请你猜想从1开始,将前10个奇数(即当最后一个奇数是19时),它们的和是。3、小王利用计算机设计了一个计算程序,输入和输出的数据如下表:输入…12345…输出……那么,当输入数据是8时,输出的数据是()A、B、C、D、4、如下左图所示,摆第一个“小屋子”要5枚棋子,摆第二个要11枚棋子,摆第三个要17枚棋子,则摆第30个“小屋子”要枚棋子.5、如下右图是某同学在沙滩上用石子摆成的小房子,观察图形的变化规律,写出第n个小房子用了块石子第4题6、如下图是用棋子摆成的“上”字:第一个“上”字第二个“上”字第三个“上”字如果按照以上规律继续摆下去,那么通过观察,可以发现:(1)第四、第五个“上”字分别需用和枚棋子;(2)第n个“上”字需用枚棋子。
7、如图一串有黑有白,其排列有一定规律的珠子,被盒子遮住一部分,则这串珠子被盒子遮住的部分有_______颗.第7题图
8、根据下列5个图形及相应点的个数的变化规律:猜想第6个图形有个点,第n个图形中有个点。 9、下面是按照一定规律画出的一列“树型”图:经观察可以发现:图(2)比图(1)多出2个“树枝”;图(3)比图(2)多出5个“树枝”;图(4)比图(3)多出10个“树枝”;照此规律,图(7)比图(6)多出个“树枝”。10、观察下面的点阵图和相应的等式,探究其中的规律:(1)在④和⑤后面的横线上分别写出相应的等式;…………①1=12;②1+3=22;③1+3+5=32;④;⑤;(2)通过猜想写出与第n个点阵相对应的等式_____________________。11、用边长为1cm的小正方形搭成如下的塔状图形,则第n次所搭图形的周长是_______________cm(用含n的代数式表示)。第1次第2次第3次第4次······12、如图,都是由边长为1的正方体叠成的图形。例如第(1)个图形的表面积为6个平方单位,第(2)个图形的表面积为18个平方单位,第(3)个图形的表面积是36个平方单位。依此规律。则第(5)个图形的表面积 个平方单位
(1)(2)(3)(4)13、图(1)是一个水平摆放的小正方体木块,图(2)、(3)是由这样的小正方体木块叠放而成,按照这样的规律继续叠放下去,至第七个叠放的图形中,小正方体木块总数应是()A25B66C91D120⑴⑵⑶14、如图是由大小相同的小立方体木块叠入而成的几何体,图⑴中有1个立方体,图⑵中有4个立方体,图⑶中有9个立方体,……按这样的规律叠放下去,第8个图中小立方体个数是.15、图1是棱长为a的小正方体,图2、图3由这样的小正方体摆放而成.按照这样的方法继续摆放,由上而下分别叫第一层、第二层、…、第n层,第n层的小正方体的个数为s.解答下列问题:图1图2图3(1)按照要求填表:
n1234…s136…(2)写出当n=10时,s=.16、如图用火柴摆去系列图案,按这种方式摆下去,当每边摆10根时(即)时,需要的火柴棒总数为根;17、用火柴棒按如图的方式搭一行三角形,搭一个三角形需3支火柴棒,搭2个三角形需5支火柴棒,搭3个三角形需7支火柴棒,照这样的规律下去,搭n个三角形需要S支火柴棒,那么用n的式子表示S的式子是_______(n为正整数).18、如图所示,用同样规格的黑、白两色正方形瓷砖铺设矩形地面,请观察下图:则第n个图形中需用黑色瓷砖____块.(用含n的代数式表示)19题图19、如图,用同样规格的黑白两种正方形瓷砖铺设正方形地面,观察图形并猜想填空:第18题图图当黑色瓷砖为20块时,白色瓷砖为块;当白色瓷砖为n2(n为正整数)块时,黑色瓷砖为块.20、观察下列由棱长为1的小立方体摆成的图形,寻找规律:如图1中:共有1个小立方体,其中1个看得见,0个看不见;如图2中:共有8个小立方体,其中7个看得见,1个看不见;如图3中:共有27个小立方体,其中有19个看得8个看不见;……,则第6个图中,看不见的小立方体有个。
21、下面的图形是由边长为l的正方形按照某种规律排列而组成的.(1)观察图形,填写下表:图形①②③正方形的个数8图形的周长18(2)推测第n个图形中,正方形的个数为________,周长为______________(都用含n的代数式表示).22、观察下图,我们可以发现:图⑴中有1个正方形;图⑵中有5个正方形,图⑶中共有14个正方形,按照这种规律继续下去,图⑹中共有_______个正方形。ADCB23、某正方形园地是由边长为1的四个小正方形组成的,现要在园地上建一个花坛(阴影部分)使花坛面积是园地面积的一半,以下图中设计不合要求的是()第22题图第23题图ABCD24、如下图中的四个正方形的边长均相等,其中阴影部分面积最大的图形是()25、如图,在方格纸中有四个图形<1>、<2>、<3>、<4>,其中面积相等的图形是()A.<1>和<2>B.<2>和<3>C.<2>和<4>D.<1>和<4>
26、某体育馆用大小相同的长方形木块镶嵌地面,第1次铺2块,如图1;第2次把第1次铺的完全围起来,如图2;第3次把第2次铺的完全围起来,如图3;…依此方法,第n次铺完后,用字母n表示第n次镶嵌所使用的木块块数为.(n为正整数)27、用黑白两种颜色的正六边形地面砖按如下所示的规律,拼成若干个图案:⑴第4个图案中有白色地面砖块;⑵第n个图案中有白色地面砖块。28、分析如下图①,②,④中阴影部分的分布规律,按此规律在图③中画出其中的阴影部分.29、将一圆形纸片对折后再对折,得到图2,然后沿着图中的虚线剪开,得到两部分,其中一部分展开后的平面图形是()图2 30.如图(1),小强拿一张正方形的纸,沿虚线对折一次得图(2),再对折一次得图(3),然后用剪刀沿图(3)中的虚线剪去一个角,再打开后的形状是()
(A) (B)(C)(D)
31、用一条宽相等的足够长的纸条,打一个结,如图(1)所示,然后轻轻拉紧、压平就可以得到如图(2)所示的正五边形ABCDE,其中∠BAC= 度.CDEBA图(2)图132、如图,一张长方形纸沿AB对折,以AB中点O为顶点将平角五等分,并沿五等分的折线折叠,再沿CD剪开,使展开后为正五角星(正五边形对角线所构成的图形).则∠OCD等于( )A.108°B.144°C.126°D.129°33、如图,把一个正方形三次对折后沿虚线剪下则得到的图形是()_沿虚线剪开ABCD第35题图34、将一张长方形的纸对折,如图5所示可得到一条折痕(图中虚线).继续对折,对折时每次折痕与上次的折痕保持平行,连续对折三次后,可以得到7条折痕,那么对折四次可以得到条折痕.如果对折n次,可以得到_____________条折痕。35、观察图形:图中是边长为1,2,3…的正方形:当边长=1
时,正方形被分成2个大小相等的小等腰直角三角形;当边长=2时,正方形被分成8个大小相等的小等腰直角三角形;当边长=3时,正方形被分成18个大小相等的小等腰直角三角形;以此类推:当边长为时,正方形被分成大小相等的小等腰直角三角形的个数是。36、水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示.如右图,是一个正方体的平面展开图,若图中的“似”表示正方体的前面,“锦”表示右面,“程”表示下面.则“祝”、“你”、“前”分别表示正方体的___________________.ASADSACSABSA程前你祝似锦37、如图是一块长方形ABCD的场地,长AB=102m,宽AD=51m,从A、B两处入口的中路宽都为1m,两小路汇合处路宽为2m,其余部分种植草坪,则草坪面积为()(A)5050m2(B)4900m2(C)5000m2(D)4998m238、读一读,想一想,做一做:国际象棋、中国象棋和围棋号称为世界三大棋种.国际象棋中的“皇后”的威力可比中国象棋中的“车”大得多:“皇后”不仅能控制她所在的行与列中的每一个小方格,而且还能控制“斜”方向的两条直线上的每一个小方格.如图甲是一个4×4的小方格棋盘,图中的“皇后Q”能控制图中虚线所经过的每一个小方格.①在如图乙的小方格棋盘中有一“皇后Q”,她所在的位置可用“(2,3)”来表示,请说明“皇后Q”所在的位置“(2,3)”的意义,并用这种表示法分别写出棋盘中不能被该“皇后Q”所控制的四个位置.②如图丙也是一个4×4的小方格棋盘,请在这个棋盘中放入四个“皇后Q”,使这四个“皇后Q”之间互不受对方控制(在图丙中的某四个小方格中标出字母Q即可).12341234Q行列乙12341234丙12341234Q甲
参考答案1、132、1003、C4、1795、3(n+1)-3+n(n+1)或(n+1)2+2n-16、(1)18、22(2)4n+27、278、31,n2-n-19、8010、1+3+5+7=42;1+3+5+7+9=52;1+3+5+……+2n-1=n211、4n12、9013、C14、645、(1)10(2)1+2+3+……+n=n(n+1)/216、16517、s=2n+118、4n+619、16,4n+420、12521、(1)13、18;28、38;(2)5n+3,10n+822、9123、B24、B25、A26、8n-627、(1)18;(2)4n+228、29、C30、C31、3632、A33、C34、15;2n-135、2n236、后面、上面、左面37、C38、(1)(1,1),(3,1),(4,2),(4,4);(2)第一讲:一次函数与反比例函数1.一次函数与正比例函数的定义:一次函数:一般地,y=kx+b若(其中k,b为常数且k≠0),那么y是x的一次函数正比例函数:当b=0,k≠0时,y=kx,此时称y是x的正比例函数2.一次函数与正比例函数的区别与联系:从解析式看:y=kx+b(k≠0,b≠0)是一次函数而y=kx(k≠0,b≠0)是正比例函数,显然正比例函数是一次函数的特例,一次函数是正比例函数的推广
从图象看:y=kx(k≠0)是过点(0,0)的一条直线,而y=kx+b(k≠0)是过点(0,b)且与y=kx平行的一条直线。例1:如图,已知直线y=-x+2与x轴,y轴分别交于点A和点B,另一直线y=kx+b(k≠0)经过点C(1,0),且把△AOB分成两部分。OBAC(1)若△AOB被分成的两部分面积相等,求k和b的值3、反比例函数的图象y=是由两支曲线组成的。(1) 当k>0时,两支曲线分别位于第一、三象限,(2) 当k<0时,两支曲线分别位于第二、四象限.例2.(1)已知函数的图象分布在第二、四象限内,则的取值范围是_________(2)若ab<0,则函数与在同一坐标系内的图象大致可能是下图中的()(A)(B)(C)(D)(2011•成都)如图,已知反比例函数的图象经过点(,8),直线y=﹣x+b经过该反比例函数图象上的点Q(4,m).(1)求上述反比例函数和直线的函数表达式;(2)设该直线与x轴、y轴分别相交于A、B两点,与反比例函数图象的另一个交点为P,连接0P、OQ,求△OPQ的面积.
解:(1)把点(,8)代入反比例函数,得k=•8=4,∴反比例函数的解析式为y=;又∵点Q(4,m)在该反比例函数图象上,∴4•m=4,解得m=1,即Q点的坐标为(4,1),而直线y=﹣x+b经过点Q(4,1),∴1=﹣4+b,解得b=5,∴直线的函数表达式为y=﹣x+5;(2)联立,解得或,∴P点坐标为(1,4),对于y=﹣x+5,令y=0,得x=5,∴A点坐标为(5,0),∴S△OPQ=S△AOB﹣S△OBP﹣S△OAQ=×5×5﹣×5×1﹣×5×1=.练习:一、选择题1、下列各点中,在函数图像上的是()A.(-2,-4);B.(2,3);C.(-6,1);D.(-,3).2、如图,A,B是双曲线上的点,A,B两点的横坐标分别是a,2a,线段AB的延长线交x轴于点C,若,则k=___________.3、如图,过x轴正半轴任意一点P作x轴的垂线,分别与反比例函数y1=和y2=的图像交于点A和点B.若点C是y轴上任意一点,连结AC、BC,则△ABC的面积为()
A.1B.2C.3D.44、已知双曲线,的部分图象如图所示,是轴正半轴上一点,过点作∥轴,分别交两个图象于点.若,则.5、如图,点A在双曲线上,且OA=4,过A作AC⊥轴,垂足为C,OA的垂直平分线交OC于B,则△ABC周长为()A.B.5C.D.6、平面直角坐标系中,已知点O(0,0)、A(0,2)、B(1,0),点P是反比例函数图象上的一个动点,过点P作PQ⊥x轴,垂足为点Q.若以点O、P、Q为顶点的三角形与△OAB相似,则相应的点P共有()A.1个B.2个C.3个D.4个7、已知反比例函数的图象过点M(-1,2),则此反比例函数的表达式为()A.y=B.y=-C.y=D.y=-8、经过点的双曲线的表达式是().A.;B.;C.;D.9、如图,已知双曲线经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(,4),则△AOC的面积为()A.12B.9C.6D.410、如图,矩形ABOC的面积为3,反比例函数的图象过点A,则k=()Oxy┐A.B.C.D.11、已知反比例函数的图象如图,则一元二次方程根的情况是()A.有两个不等实根B.有两个相等实根
C.没有实根D.无法确定。12、下列函数中,y随x增大而减小的是( )A.y=—B.y=C.y=-D.y=-x-113、如图,已知梯形ABCO的底边AO在轴上,BC∥AO,AB⊥AO,过点C的双曲线交OB于D,且OD:DB=1:2,若△OBC的面积等于3,则k的值()A.等于2B.等于C.等于D.无法确定14、反比例函数与一次函数y=mx-m(m≠0)在同一平面直角坐标系中的图像可能是()15、若反比例函数y=的图象经过点(-2,1),则此函数的图象一定经过点()A.(-2,-1)B.(2,-1)C.(,2)D.(,2)16、如图所示,两个反比例函数和在第一象限内的图象依次是和,设点在上,⊥轴于点,交于点,⊥轴于点,交于点,则四边形的面积为() A.B.C.D.17、若点都在反比例函数的图象上,则()A.B.C.D.18、下列函数中,y随x的增大而减小的是()
A.;B.;C.;D..19、若反比例函数的图象经过点(-1,2),则这个函数的图象一定经过点() A、(2,-1) B、(,2) C、(-2,-1) D、(,2)20、若反比例函数的图象位于第二、四象限内,则m的取值范围是( )A.m>0B.m<0C.m>1D.m<121、已知反比例函数的图象经过点(-1,2),则这个函数的图象位于()A.第一、三象限B.第二、三象限C.第二、四象限D.第三、四象限22、反比例函数y=,当x>0时,y随x的增大而增大,那么m的取值范围是()(A)m<3(B)m>3(C)m<-3(D)m>-3二、填空题1、点,点是双曲线上的两点,若,则(填“=”、“>”、“<”).2、如果点A、B在一个反比例函数的图像上,点A的坐标为(1,2),点B横坐标为2,那么A、B两点之间的距离为.3、已知反比例函数的图像经过点(m,3)和(-3,2),则m的值为.4、若反比例函数的图象经过点(-2,-1),则这个函数的图象位于第___________象限.5、设函数与的图象的交点坐标为(,),则的值为_____.6、如果,,那么 .7、某中学要在校园内划出一块面积是100m2的矩形土地做花圃,设这个矩形的相邻两边的长分别为xm和ym,那么y关于x的函数解析式是_________________.8、反比例函数y=的图象与正比例函数y=3x的图象交于O点P(m,6),则反比例函数的关系式是.9、如图,已知点A在双曲线上,过点A作AC⊥x轴于点C,OC=,线段OA的垂直平分线交OC于点B,则△ABC的周长为 .10、若反比例函数y=(k-1)的图象经过第二、四象限,则k=.11、一个函数具有下列性质:
1xyS1S2S3P1P2P3O234①它的图像经过点(-1,1);②它的图像在二、四象限内;③在每个象限内,函数值y随自变量x的增大而增大.则这个函数的解析式可以为.12、如图,在反比例函数()的图象上,有点,···,,它们的横坐标依次为1,2,3,4,···,.分别过这些点作轴与轴的垂线,图中所构成的阴影部分的面积分别为,···,,则的值为.ABPxyO13、如图,A是反比例函数y=图象上一点,过点A作AB⊥y轴于点B,点P在x轴上,△ABP的面积为2,则K的值为_____________.14、如图,△AOB为等边三角形,点B的坐标为(-2,0),过点C(2,0)作直线l交AO于D,交AB于E,点E在某反比例函数图象上,当△ADE和△DCO的面积相等时,那么该反比例函数解析式为 .三、解答题1、已知双曲线和直线AB的图象交于点A(-3,4),AC⊥x轴于点C.(1)求双曲线的解析式;(2)当直线AB绕着点A转动时,与x轴的交点为B(a,0),并与双曲线另一支还有一个交点的情形下,求△ABC的面积S与a之间的函数关系式.,并指出a的取值范围.
2、已知反比例函数的图像经过第二象限内的点A(-1,m),AB⊥x轴于点B,△AOB的面积为2.若直线经过点A,并且经过反比例函数的图象上另一点C(n,一2).⑴求直线的解析式;⑵设直线与x轴交于点M,求AM的长.3、如图,在以O为原点的直角坐标系中,点A、C分别在x轴、y轴的正半轴上,点B(a,b)在第一象限,四边形OABC是矩形,若反比例函数(k>0,x>0)的图象与AB相交于点D,与BC相交于点E,且BE=CE.(1)求证:BD=AD;(2)若四边形ODBE的面积是9,求k的值.4、如图,将—矩形OABC放在直角坐际系中,O为坐标原点.点A在x轴正半轴上.点E是边AB上的—个动点(不与点A、B重合),过点E的反比例函数的图象与边BC交于点F.(1)若△OAE、△OCF的而积分别为.且,求k的值.(2)若OA=2,0C=4,问当点E运动到什么位置时,四边形OAEF
的面积最大,其最大值为多少?5、如图,在平面直角坐标系中,一次函数y=-2x的图像与反比例函数的图像的一个交点为A(-1,n).(1)求反比例函数的解析式;(2)若P是坐标轴上的一点,且满足PA=0A,直接写出P的坐标.6、如图,一次函数与反比例函数在第一象限的图象交于点,且点的横坐标为1,过点作轴的垂线,为垂足,若,求一次函数和反比例函数的解析式.7、已如图,反比例函数y=的图象与一次函数y=mx+b的图象交于两点A(1,3),B(n,-1).(1)求反比例函数与一次函数的函数关系式;
yxAOB(2)根据图象,直接回答:当x取何值时,一次函数的值大于反比例函数的值;(3)连接AO、BO,求△ABO的面积;8、如图,已知A(4,a),B(-2,-4)是一次函数y=kx+b的图象和反比例函数的图象的交点.(1)求反比例函数的解析式;(2)求一次函数的解析式。AB(1,n)1-1-2nyOx9、如图,一次函数的图象与反比例函数的图象交于A、B两点。(1)利用图中条件求反比例函数和一次函数的解析式;(2)根据图象写出使一次函数的值大于反比例函数的值的的取值范围.10、如图,在平面直角坐标系xOy中,反比例函数()的图象与一次函数
的图象的一个交点为.(1)求一次函数的解析式;(2)设一次函数的图象与y轴交于点B,P为一次函数的图象上一点,若的面积为5,求点P的坐标.11、已知A(n,-2),B(1,4)是一次函数y=kx+b的图象和反比例函数y=的图象的两个交点,直线AB与y轴交于点C.(1)求反比例函数和一次函数的关系式;(2)求△AOC的面积;(3)求不等式kx+b-<0的解集(直接写出答案).12、如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOB=60°,点A在第一象限,过点A的双曲线为.在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是O´B´.(1)当点O´与点A重合时,求点P的坐标.(2)设P(t,0),当O´B´与双曲线有交点时,t的取值范围是多少?
14、如图,一次函数与反比例函数的图像交于点A(4,m)和B(-8,-2),与y轴交于点C,求:(1),;(2)根据函数图像可知,当>时,x的取值范围是;(3)过点A作轴于点D,点P是反比例函数在第一象限图像上的一点,设直线OP与线段AD交于点E,当时,求点P的坐标。15、如图,反比例函数的图像经过点,过点作轴于点B,△AOB的面积为.(1)求和的值;(2)若一次函数的图象经过点,求这个一次函数的解析式.6OAB16、如图所示,一次函数与反比例函数的图象相交于A,B两点,且与坐标轴的交点为,,点B的横坐标为-4.(1)试确定反比例函数的解析式;(2)求△AOB的面积;(3)直接写出不等式的解.
17、如图,直线分别交轴,轴于点,点是直线与双曲线在第一象限内的交点,轴,垂足为点,的面积为4.(1)求点的坐标;(2)求双曲线的解析式及直线与双曲线另一交点的坐标.20.(2006)如图,已知反比例函数y=(k<0)的图象经过点A(-,m),过点A作AB⊥x轴于点B,且△AOB的面积为.(1)求k和m的值;(2)若一次函数y=ax+1的图象经过点A,并且与x轴相交于点C,求∠ACO的度数和│AO│∶│AC│(2008)如图,已知反比例函数y=的图象经过点A(1,-3),一次函数y=kx+b的图象经过点A与点C(0,-4),且与反比例函数的图象相交于另一点B.ABOxy(1)试确定这两个函数的表达式;(2)求点B的坐标.
(2011绵阳)右图中曲线是反比例函数的图象的一支.(1)这个反比例函数图象的另一支位于哪个象限?常数n的取值范围是什么?(2)若一次函数的图象与反比例函数的图象交于点A,与x轴交于点B,△AOB的面积为2,求n的值.第二讲:二次函数一、y=ax2,y=ax2+c二次函数y=ax2的图象的一些性质:①、图象——“抛物线”是轴对称图形;②、与x、y轴交点——(0,0)即原点;(与x、y轴交点——(0,c))③、a的绝对值越大抛物线开口越大,a﹥0,开口向上:当x﹤0时,(对称轴左侧),y随x的增大而减小(y随x的减小而增大)当x﹥0时,(对称轴右侧),y随x的增大而增大(y随x的减小而减小) a﹤0,开口向下:当x﹤0时,(对称轴左侧),y随x的增大而增大(y随x的减小而减小)当x﹥0时,(对称轴右侧),y随x的增大而减小(y随x的减小而增大)二、y=a(x-h)2,y=a(x-h)2+k1、画y=a(x-h)2+k(a≠0)的图像,列表时:在对称轴x=h两侧对称取点.2、y=a(x-h)2+k(a≠0)具有以下性质:抛物线对称轴顶点坐标开口方向y=a(x-h)2+k(a>0)x=h(h,k)向上y=a(x-h)2+k(a<0)x=h(h,k)向下三、y=ax2+bx+c(a、b、c是常数,a≠0)y=ax2+bx+c化为y=a(x+)2+,对照y=a(x-h)2+k的形式得对称轴为x=-,
顶点坐标为(-,)关于二次函数变换:1、比较函数y=3x2与y=3(x-1)2的图象的性质.2、在同一直角坐标系中比较函数y=3(x-1)2和y=3(x-1)2+2的图象性质总结:一般地,平移二次函数y=ax2的图象便可得到二次函数为y=ax2+c,y=a(x-h)2,y=a(x-h)2+k的图象.(1)将y=ax2的图象上下移动便可得到函数y=ax2+c的图象,当c>0时,向上移动,当c<0时,向下移动.(2)将函数y=ax2的图象左右移动便可得到函数y=a(x-h)2的图象,当h>0时,向右移动,当h<0时,向左移动.(3)将函数y=ax2的图象既上下移,又左右移,便可得到函数y=a(x-h)+k的图象.因此,这些函数的图象都是一条抛物线,它们的开口方向,对称轴和顶点坐标与a,h,k的值有关.基础练习:一、选择题1、已知+=y,其中与成反比例,且比例系数为,而与成正比例,且比例系数为,若x=-1时,y=0,则,的关系是()A.=0B.=1C.=0D.=-12、已知二次函数,为常数,当y达到最小值时,x的值为()(A)(A);(B);(C);(D)3、若二次函数的顶点在第一象限,且经过点(0,1),(-1,0),则S=a+b+c的变化范围是()(A)0
1;(C)10,△>0;B.a>0,△<0;C.a<0,△<0;D.a<0,△<0二、填空题:5、已知方程组的解也是二元一次方程x-y=1的一个解,则a=_________。6、已知直线与轴,轴围成一个三角形,则这个三角形面积为。
7、若m<-1,则下列函数:①;②y=-mx+1;③y=mx;④y=(m+1)x中,y随x增大而增大的是___________。8、已知二次函数(a≥1)的图像上两点A、B的横坐标分别是-1、2,点O是坐标原点,如果△AOB是直角三角形,则△OAB的周长为 。三、解答题:9、已知不等式的最小整数解是方程的解,求a的值。10、已知二次函数y=x2+bx+c的图像与x轴的两个交点的横坐标分别为x1、x2,一元二次方程x2+b2x+20=0的两实根为x3、x4,且x2-x3=x1-x4=3,求二次函数的解析式,并写出顶点坐标。答案:一、CBAB二、5、-6、187、(1)(2)8、10、y=x2+3x+2(-3/2,-1/4)巩固提高:1、(陕西中考)若正比例函数的图像经过点(-1,2),则这个图像必经过点()A.(1,2)B.(-1,-2)C.(2,-1)D.(1,-2)2、(安徽中考)已知函数的图象如图,则的图象可能是()3、(黄冈中考)小高从家门口骑车去单位上班,先走平路到达点A,再走上坡路到达点B
,最后走下坡路到达工作单位,所用的时间与路程的关系如图所示.下班后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别保持和去上班时一致,那么他从单位到家门口需要的时间是()A.12分钟B.15分钟C.25分钟D.27分钟OBCA图5AOBC第4题图4、(广东深圳)如图,反比例函数的图象与直线的交点为A,B,过点A作y轴的平行线与过点B作x轴的平行线相交于点C,则的面积为( )A.8B.6C.4D.25、(广西河池)如图5,A、B是函数的图象上关于原点对称的任意两点,BC∥轴,AC∥轴,△ABC的面积记为,则()A.B.C.D.6、函数在同一直角坐标系内的图象大致是()图27、已知二次函数y=ax2+bx+c(a≠0)的图象如图2所示,给出以下结论:①a+b+c<0图图;②a-b+c<0;③b+2a<0;④abc>0.其中所有正确结论的序号是( )A.③④B.②③ C.①④ D.①②③8、二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),其中正确结论的个数是( )
A.4个B.3个C.2个D.1个考点:二次函数图象与系数的关系.分析:利用二次函数图象的相关知识与函数系数的联系,需要根据图形,逐一判断.解答:解:∵抛物线和x轴有两个交点,∴b2﹣4ac>0,∴4ac﹣b2<0,∴①正确;∵对称轴是直线x﹣1,和x轴的一个交点在点(0,0)和点(1,0)之间,∴抛物线和x轴的另一个交点在(﹣3,0)和(﹣2,0)之间,∴把(﹣2,0)代入抛物线得:y=4a﹣2b+c>0,∴4a+c>2b,∴②错误;∵把(1,0)代入抛物线得:y=a+b+c<0∴2a+2b+2c<0,∵b=2a,∴3b,2c<0,∴③正确;∵抛物线的对称轴是直线x=﹣1,∴y=a﹣b+c的值最大,即把(m,0)(m≠0)代入得:y=am2+bm+c<a﹣b+c,∴am2+bm+b<a,即m(am+b)+b<a,∴④正确;即正确的有3个,9、已知二次函数y=ax2+bx+c(a≠0)的图象如图,且关于x的一元二次方程ax2+bx+c﹣m=0没有实数根,有下列结论:①b2﹣4ac>0;②abc<0;③m>2.其中,正确结论的个数是( ) A.0B.1C.2D.3解答:解:①∵二次函数y=ax2+bx+c与x轴有两个交点,∴b2﹣4ac>0,故①正确;②∵抛物线的开口向下,∴a<0,∵抛物线与y轴交于正半轴,∴c>0,∵对称轴x=﹣>0,∴ab<0,∵a<0,∴b>0,∴abc<0,故②正确;③∵一元二次方程ax2+bx+c﹣m=0没有实数根,∴y=ax2+bx+c和y=m没有交点,由图可得,m>2,故③正确.故选D.10、当﹣2≤x≤1时,二次函数y=﹣(x﹣m)2+m2+1有最大值4,则实数m的值为( ) A.B.或C.2或D.2或﹣或
解答:解:二次函数的对称轴为直线x=m,①m<﹣2时,x=﹣2时二次函数有最大值,此时﹣(﹣2﹣m)2+m2+1=4,解得m=﹣,与m<﹣2矛盾,故m值不存在;②当﹣2≤m≤1时,x=m时,二次函数有最大值,此时,m2+1=4,解得m=﹣,m=(舍去);③当m>1时,x=1时,二次函数有最大值,此时,﹣(1﹣m)2+m2+1=4,解得m=2,综上所述,m的值为2或﹣.故选C.11、抛物线y=ax2+bx+c的顶点为D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:①b2﹣4ac<0;②a+b+c<0;③c﹣a=2;④方程ax2+bx+c﹣2=0有两个相等的实数根.其中正确结论的个数为( C )A、1个B、2个C、3个D、4个12、(钦州中考)一次函数的图象过点(0,2),且函数y的值随自变量x的增大而增大,请写出一个符合条件的函数解析式:__.13、(绍兴中考)如图,已知函数和的图象交点为,则不等式的解集为.第14题图Oxy1Py=x+by=ax+314、(湖北黄石)如图所示,P1(x1,y1)、P2(x2,y2),……Pn(xn,yn)在函数y=(x>0)的图象上,△OP1A1,△P2A1A2,△P3A2A3……△PnAn-1An……都是等腰直角三角形,斜边OA1,A1A2……An-1An,都在x轴上,则y1+y2+…yn=。15.(天津市)已知图中的曲线是反比例函数(为常数)图象的一支.(Ⅰ)这个反比例函数图象的另一支在第几象限?常数的取值范围是什么?(Ⅱ)若该函数的图象与正比例函数的图象在第一象内限的交点为,过点作
轴的垂线,垂足为,当的面积为4时,求点的坐标及反比例函数的解析式.xyO16、(浙江嘉兴)如图,曲线C是函数在第一象限内的图象,抛物线是函数的图象.点()在曲线C上,且都是整数.(1)求出所有的点;(2)在中任取两点作直线,求所有不同直线的条数;(3)从(2)的所有直线中任取一条直线,求所取直线与抛物线有公共点的概率.(第12题)642246yxO
17.某商店经销一种销售成本为每千克40元的水产品.据市场分析,若按每千克50元销售,一个月能售出500kg;销售单价每涨1元,月销售量就减少10kg.针对这种水产品的销售情况,请解答以下问题:(1)当销售单价定为每千克55元时,计算月销售量和月销售利润;(2)设销售单价为每千克x元,月销售利润为y元,求y与x的函数关系式;(3)商店想在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,销售单价应定为多少?31,解:(1)按每千克50元销售,一个月能售出500kg,销售单价每涨1元,月销售量就减少10kg。现在单价定为每千克55元,即涨了5元,所以月销售量减少50kg,所以月销售量为500-50=450kg,月销售利润为(55-40)×450=6750元。(2)设销售单价为每千克x元,则上涨了x-50元,月销售量减少(x-50)×10kg,即月销售量为500-10(x-50),所以利润为y=[500-10(x-50)]×(x-40),即(3)月销售利润达到8000元,即,解得x=60或x=80当x=60时,销售量为500-10(60-50)=400,当x=80时,销售量为500-10(80-50)=200而月销售量不超过10000元,即销售量不超过,而400>250,所以x=60应舍去,所以销售单价应定于80元。18、(重庆市江津区)抛物线与x轴交与A(1,0),B(-3,0)两点,(1)求该抛物线的解析式;(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.(3)在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面积最大?,若存在,求出点P的坐标及△PBC的面积最大值.若没有,请说明理由.19、(湖北省荆门市)一开口向上的抛物线与x轴交于A(,0),B(m+2,0)两点,记抛物线顶点为C,且AC⊥BC.(1)若m为常数,求抛物线的解析式;
(2)若m为小于0的常数,那么(1)中的抛物线经过怎么样的平移可以使顶点在坐标原点?(3)设抛物线交y轴正半轴于D点,问是否存在实数m,使得△BCD为等腰三角形?若存在,求出m的值;若不存在,请说明理由.OBACDxy第15题图20.已知经过原点的抛物线y=-2x2+4x(如图所示)与x的另一交点为A现将它向右平移m(m>0)位,所得抛物线与x轴交于C、D点,与原抛物线交于点P(1)求点P的坐标(可用含m式子表示)(2)设△PCD的面积为s,求s关于m关系式.(3)过点P作x轴的平行线交原抛物线于点E,交平移后的抛物线于点F.请问是否存在m,使以点E、O、A、F为顶点的四边形为平行四边形.若存在,求出m的值,若不存在,请说明理由.考点:二次函数综合题.分析:(1)首先将抛物线表示出顶点式的形式,再进行平移,左加右减,即可得出答案;(2)求出抛物线与x轴的交点坐标,根据当0<m<2,当m=2,即点P在x轴时,当m>2即点P在第四象限时,分别得出即可;(3)根据E、O、A、F为顶点的四边形是平行四边形,则EF=OA=2由轴对称可知PE=PF,表示出E点的坐标,再把点E代入抛物线解析式得出即可.
解答:解:(1)原抛物线:y=-2x2+4x=-2(x-1)2+2,则平移后的抛物线为:y=-2(x-1-m)2+2,由题得,解得,∴点P的坐标为(,);(2)抛物线:y=-2x2+4x=-2x(x-2)∴抛物线与x轴的交点为O(0,0)A(2,0),∴AC=2,∵C、D两点是抛物线y=-2x2+4x向右平移m(m>0)个,单位所得抛物线与x轴的交点∴CD=OA=2,①当0<m<2,即点P在第一象限时,如图1,作PH⊥x轴于H.∵P的坐标为(,),∴PH=,∴S=CD•2•(-m2+2)=-m2+2,
②当m=2,即点P在x轴时,△PCD不存在,③当m>2即点P在第四象限时,如图2,作PH⊥x轴于H.∵P的坐标为(,),∴PH=,∴S=CD•HP=×2×=m2-2;(3)如图3若以E、O、A、F为顶点的四边形是平行四边形,则EF=OA=2由轴对称可知PE=PF,∴PE=,∵P(,),∴点E的坐标为(,),把点E代入抛物线解析式得:,第三讲:二次函数应用一、动点问题(一)、因动点产生的面积关系QPPAxyBO例1、在平面直角坐标系中,△BCD的边长为3cm的等边三角形,动点P、Q同时从点A、O两点出发,分别沿AO、OB方向匀速移动,它们的速度都是1cm/s,当点P到达点O时,P、Q两点停止运动.设点P的运动时间为t(s),解答下列问题:(1)求OA所在直线的解析式;(2)当t为何值时,△POQ是直角三角形;(3)是否存在某一时刻t,使四边形APQB的面积是△AOB面积的三分之二?若存在,求出相应的t值;若不存在,请说明理由.解:⑴根据题意:AP=tcm,BQ=tcm.△ABC中,AB=BC=3cm,∠B=60°,∴BP=(3-t)cm.△PBQ中,BP=3-t,BQ=t,
若△PBQ是直角三角形,则∠BQP=90°或∠BPQ=90°.当∠BQP=90°时,BQ=BP.即t=(3-t),t=1(秒).当∠BPQ=90°时,BP=BQ.3-t=t,t=2(秒).答:当t=1秒或t=2秒时,△PBQ是直角三角形.…………………4′⑵过P作PM⊥BC于M.Rt△BPM中,sin∠B=,∴PM=PB·sin∠B=(3-t).∴S△PBQ=BQ·PM=·t·(3-t).∴y=S△ABC-S△PBQ=×32×-·t·(3-t)=.∴y与t的关系式为:y=.…………………6′假设存在某一时刻t,使得四边形APQC的面积是△ABC面积的,则S四边形APQC=S△ABC.∴=××32×.∴t2-3t+3=0.∵(-3)2-4×1×3<0,∴方程无解.∴无论t取何值,四边形APQC的面积都不可能是△ABC面积的.……8′例2、如图,边长为1的正方形OABC的顶点O为坐标原点,点A在x轴的正半轴上,点C
在y轴的正半轴上.动点D在线段BC上移动(不与B,C重合),连接OD,过点D作DE⊥OD,交边AB于点E,连接OE.记CD的长为t.(1)当t=时,求直线DE的函数表达式;(2)如果记梯形COEB的面积为S,那么是否存在S的最大值?若存在,请求出这个最大值及此时t的值;若不存在,请说明理由;解:(1)易知△CDO∽△BED,所以,即,得BE=,则点E的坐标为E(1,).……………………………(2分)设直线DE的一次函数表达式为y=kx+b,直线经过两点D(,1)和E(1,),代入y=kx+b得,,故所求直线DE的函数表达式为y=.…………………………(2分) (注:用其它三角形相似的方法求函数表达式,参照上述解法给分)(2)存在S的最大值.………………………………………………1分求最大值:易知△COD∽△BDE,所以,即,BE=t-t2,……1分×1×(1+t-t2).………………………1分故当t=时,S有最大值.……………………………2分(二)因动直线产生的面积关系例3.如图所示,已知抛物线y=x2+bx+c经过点(1,-5)和(-2,4).(1)求这条抛物线的解析式.(2)设此抛物线与直线y=x相交于点A,B(点B在点A的右侧),平行于x轴的直线x=m(00,-y表示点E到OA的距离.∵OA是的对角线,∴.因为抛物线与轴的两个交点是(1,0)的(6,0),所以,自变量的取值范围是1<<6.①根据题意,当S=24时,即.化简,得解之,得故所求的点E有两个,分别为E1(3,-4),E2(4,-4).点E1(3,-4)满足OE=AE,所以是菱形;点E2(4,-4)不满足OE=AE,所以不是菱形.②当OA⊥EF,且OA=EF时,是正方形,此时点E的坐标只能是(3,-3).而坐标为(3,-3)的点不在抛物线上,故不存在这样的点E,使为正方形.例5.如图所示,在平面直角坐标系xOy中,矩形OABC的边长OA、OC的长分剔为12cm、6
cm,点A、C分别在y轴的负半轴和x轴的正半轴上,抛物线y=ax2+bx+c经过点A、B,且18a+c=0.(1)求抛物线的解析式;(2)如果点P由点A开始沿AB边以1cm/s的速度向点B移动,同时点Q由点B开始沿BC边以2cm/s的速度向点C移动.①移动开始后第t秒时,设△PBQ的面积为S,试写出S与t之间的函数关系式,并写出t的取值范围;QPCAxyBO②当S取得最小值时,在抛物线上是否存在点R,使得以P、B、Q、R为顶点的四边形是平行四边形?如果存在,求出R点的坐标,如果不存在,请说明理由.解:(1)据题意知:A(0,-12),B(6,-12)∵A点在抛物线上,∴C=-12∵18a+c=0,∴a=………(1分)由AB=6知抛物线的对称轴为:x=3即:∴抛物线的解析式为:…(3分)(2)①由图象知:PB=6-t,BQ=2t∴S==……(4分)即(0≤t≤1)………………(5分)②假设存在点R,可构成以P、B、R、Q为顶点的平行四边形.∵(0≤t≤1)∴当t=时,S取得最小值9.………………………………………(6分)这时PB=6-3=3,BQ=6,P(3,-12),Q(6,-6)………(7分)分情况讨论:A】假设R在BQ的右边,这时QRPB,∵P(3,-12),PB=3,Q(6,-6)R的横坐标为9,R的纵坐标为-6,即(9,-6)代入,左右两边不相等∴这时R(9,-6)不在抛物线上.……………………………………(8分)B】假设R在BQ的左边,这时PRQB,则:R的横坐标为3,纵坐标为-6,即(3,-6)代入,左右两边不相等,R不在抛物线上.…………(9分)C】假设R在PB的下方,这时PRQB,则:R(6,-18)代入,左右两边相等,R(6,-18)在抛物线上.综上所述,存点一点R(6,-18)满足题意.…………………………(10分)同步练习1、已知抛物线与轴相交于两点(点在点的左边),与
轴的负半轴相交于点,(1)求抛物线的解析式;BOAAC(2)在抛物线上是否存在点,使?如果存在,请确定点的位置,并求出点的坐标:如果不存在,请说明理由.2、如图,抛物线与轴交于点、B两点,抛物线的对称轴为直线x=1,QCAxyBO(1)求的值及抛物线的解析式;(2)过A的直线与抛物线的另一交点C的横坐标为2.直线AC的解析式;(3)点Q是抛物线上的一个动点,在x轴上是否存在点F,使得以点A、C、F、Q为顶点四边形是平行四边形?若存在,请求出所有满足条件的点F的坐标;若不存在,请说明理由.yxDCAOB3、如图,已知二次函数的图象与轴交于点,点,与轴交于点,其顶点为,直线的函数关系式为,又.(1)求二次函数的解析式和直线的函数关系式;(2)抛物线上是否存在一点P,使△PBC以BC为直角边的直角三角形?若存,求出点P的坐标;若不存在,说明理由.
4、如图,在平面直角坐标系xOy中,抛物线的对称轴为直线x=2,该抛物线与x轴交干A、B两点(B在A的右侧),与y轴交于点C,且B、C的坐标分别为(3,0)、(0,3).(1)求此抛物线的解析式;(2)抛物线上是否存在一点P,使△PAC是直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.OBCAA(三)、因动点产生的三角形相似问题例6.如图,直线与轴,轴分别相交于点,点,经过两点的抛物线与轴的另一交点为,顶点为,且对称轴是直线.(1)求点的坐标;(2)求该抛物线的函数表达式;(3)连结.请问在轴上是否存在点,使得以点为顶点的三角形与相似,若存在,请求出点的坐标;若不存在,请说明理由.解:(1)直线与轴相交于点,当时,,
点的坐标为.…………………………(1分)又抛物线过轴上的两点,且对称轴为,根据抛物线的对称性,点的坐标为.…………………………(2分)(2)过点,易知,.-----(3分)又抛物线过点,(4分)解,得(5分).(6分)(3)连结,由,得,设抛物线的对称轴交轴于点,在中,,.由点易得,在等腰直角三角形中,,由勾股定理,得.(7分)假设在轴上存在点,使得以点为顶点的三角形与相似.①当,时,.即,,又,点与点重合,的坐标是.(9分)②当,时,.即,.,
的坐标是.(11分).点不可能在点右侧的轴上(无此判断,亦不扣分).综上所述,在轴上存在两点,能使得以点为顶点的三角形与相似.(12分)同步练习1、如图,在直角坐标系中,为原点,抛物线与轴的负半轴交于点,与轴的正半轴交于点B,tan∠ACO=.(1)求抛物线的解析式;AOBCxy(2)若直线与线段交于点(不与点重合),则是否存在这样的直线,使得以为顶点的三角形与相似?若存在,求出该直线的函数表达式及点的坐标;若不存在,请说明理由.(五)、其它二次函数的综合问题例7、如图,一元二次方程的二根()是抛物线与轴的两个交点的横坐标,且此抛物线过点.xyA(3,6)QCOBP(1)求此二次函数的解析式.(2)设此抛物线的顶点为,对称轴与线段相交于点,求点和点的坐标.
(3)在轴上有一动点,当取得最小值时,求点的坐标.解:(1)解方程得1分抛物线与轴的两个交点坐标为:2分设抛物线的解析式为3分在抛物线上4分抛物线解析式为:5分(2)由6分抛物线顶点的坐标为:,对称轴方程为:7分设直线的方程为:在该直线上解得直线的方程为:9分将代入得点坐标为10分xyA(3,6)QCOBP(3)作关于轴的对称点,连接;与轴交于点即为所求的点11分设直线方程为解得直线:12分令,则13分点坐标为14分
同步练习1、如图所示,在平面直角坐标系中,抛物线经过点A(3,0)、B(5,0)、C(0,5)三点.(1)求该抛物线的函数表达式;(2)设抛物线的顶点为D,求△BCD的面积;AOBCxy(3)在抛物线的对称轴上有一个动点P,当△0CP是腰长为5的等腰三角形时,求点P的坐标.2、如图,已知抛物线与x轴的一个交点A(3,0).(1)分别求出这条抛物线与x轴的另一个交点B及与y轴的交点C的坐标; (2)设抛物线的顶点为D,求直线CD的解析式;x1234-1-2-1-2-3123yOACDB (3)求tan∠DAC的值.
辅导:弧长和扇形的面积、圆锥的侧面积和全面积一、弧长和扇形的面积:『活动一』因为360°的圆心角所对弧长就是圆周长C=2πR,所以1°的圆心角所对的弧长是.这样,在半径为R的圆中,n°的圆心角所对的弧长l=.『活动二』类比弧长的计算公式可知:在半径为R的圆中,圆心角为n°的扇形面积的计算公式为:S=.『活动三』扇形面积的另一个计算公式比较扇形面积计算公式与弧长计算公式,可以发现:可以将扇形面积的计算公式:S=πR2化为S=·R,从面可得扇形面积的另一计算公式:S=.二、圆锥的侧面积和全面积:1.圆锥的基本概念:的线段SA、SA1……叫做圆锥的母线,的线段叫做圆锥的高.2.圆锥中的各元素与它的侧面展开图——扇形的各元素之间的关系:将圆锥的侧面沿母线l剪开,展开成平面图形,可以得到一个扇形,设圆锥的底面半径为r,这个扇形的半径等于,扇形弧长等于.3.圆锥侧面积计算公式圆锥的母线即为扇形的半径,而圆锥底面的周长是扇形的弧长,这样,S圆锥侧=S扇形=·2πr·l=πrl4.圆锥全面积计算公式S圆锥全=S圆锥侧+S圆锥底面=πrl+πr2=πr(l+r)三、例题讲解:例1、(2011•德州,11,4分)母线长为2,底面圆的半径为1的圆锥的侧面积为.例2、(2011年山东省东营市,21,9分)如图,已知点A、B、C、D均在已知圆上,AD∥BC,BD平分∠ABC,∠BAD=120°,四边形ABCD的周长为15.(1)求此圆的半径;(2)求图中阴影部分的面积.
例3、(2010广东,14,6分)如图,在平面直角坐标系中,点P的坐标为(-4,0),⊙P的半径为2,将⊙P沿x轴向右平移4个单位长度得⊙P1.(1)画出⊙P1,并直接判断⊙P与⊙P1的位置关系;(2)设⊙P1与x轴正半轴,y轴正半轴的交点分别为A,B,求劣弧AB与弦AB围成的图形的面积(结果保留π).yx-3O123123-3-2-1-1-2-4-5-6例3图四、同步练习:1、(2012北海,11,3分)如图,在边长为1的正方形组成的网格中,△ABC的顶点都在格点上,将△ABC绕点C顺时针旋转60°,则顶点A所经过的路径长为:()ABCOD第2题图ABCDEF(第3题)OA.10πB.C.πD.πABC第1题图2、(2012北海,12,3分)如图,等边△ABC的周长为6π,半径是1的⊙O从与AB相切于点D的位置出发,在△ABC外部按顺时针方向沿三角形滚动,又回到与AB相切于点D的位置,则⊙O自转了:()A.2周B.3周C.4周D.5周3、(2012湖北咸宁,7,3分)如图,⊙O的外切正六边形ABCDEF的边长为2,则图中阴影部分的面积为().A.B.C.D.4、(2012四川内江,8,3分)如图2,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2
,则阴影部分图形的面积为()第11题A.4πB.2πC.πD.第9题ABDCO图25、(2012·湖南省张家界市·14题·3分)已知圆锥的底面直径和母线长都是10,则圆锥的侧面积为________.6、(2012·哈尔滨,题号16分值3)一个圆锥的母线长为4,侧面积为8,则这个圆锥的底面圆的半径是.7、(2012江苏省淮安市,17,3分)若圆锥的底面半径为2cm,母线长为5cm,则此圆锥的侧面积为cm2.8、(2012四川达州,11,3分)已知圆锥的底面半径为4,母线长为6,则它的侧面积是.(不取近似值)9、(2012年广西玉林市,16,3)如图,矩形OABC内接于扇形MON,当CN=CO时,∠NMB的度数是.ABCl…………图610、(2012广安中考试题第15题,3分)如图6,Rt△ABC的边BC位于直线l上,AC=,∠ACB=90o,∠A=30o,若△RtABC由现在的位置向右无滑动地翻转,当点A第3次落在直线上l时,点A所经过的路线的长为________________(结果用含л的式子表示).第12题图AOBDC11、(2011•丹东,14,3分)如图,将半径为3cm的圆形纸片剪掉三分之一,余下部分围成一个圆锥的侧面,则这个圆锥的高是 .12、(2012贵州贵阳,23,10分)如图,在⊙O中,直径AB=2,CA切⊙O于A,BC交⊙O于D,若∠C=45°,则(1)BD的长是;(5分)(2)求阴影部分的面积.(5分)13、(2012浙江省义乌市,20,8分)如图,已知AB是⊙O的直径,点C、D在⊙O上,OABCDE点E在⊙O外,∠EAC=∠D=60°.
(1)求∠ABC的度数;(2)求证:AE是⊙O的切线;(3)当BC=4时,求劣弧AC的长.14、(2012年吉林省,第23题、7分.)如图,在扇形OAB中,∠AOB=90°,半径OA=6.将扇形OAB沿过点B的直线折叠.点O恰好落在弧AB上点D处,折痕交OA于点C,求整个阴影部分的周长和面积.15、(2011甘肃兰州,25,9分)如图,在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.(1)请完成如下操作:①以点O为原点、竖直和水平方向所在的直线为坐标轴、网格边长为单位长,建立平面直角坐标系;②用直尺和圆规画出该圆弧所在圆的圆心D的位置(不用写作法,保留作图痕迹),并连结AD、CD.(2)请在(1)的基础上,完成下列问题:①写出点的坐标:C、D;②⊙D的半径=(结果保留根号);③若扇形ADC是一个圆锥的侧面展开图,则该圆锥的底面面积为(结果保留π);④若E(7,0),试判断直线EC与⊙D的位置关系并说明你的理由.ABCO参考答案:例1、考点:圆锥的计算。专题:计算题。
分析:先计算出底面圆的周长,它等于圆锥侧面展开图扇形的弧长,而母线长为扇形的半径,然后根据扇形的面积公式计算即可.解答:解:∵圆锥的底面圆的半径为1,∴圆锥的底面圆的周长=2π×1=2π,∴圆锥的侧面积=×2π×2=2π.故答案为:2π.点评:本题考查了圆锥的侧面积公式:S=.圆锥侧面展开图为扇形,底面圆的周长等于扇形的弧长,母线长为扇形的半径.例2、考点:扇形面积的计算;圆心角、弧、弦的关系;圆周角定理.专题:几何图形问题.分析:(1)根据条件可以证得四边形ABCD是等腰梯形,且AB=AD=DC,∠DBC=90°,在直角△BDC中,BC是圆的直径,BC=2DC,根据四边形ABCD的周长为15,即可求得BC,即可得到圆的半径;(2)根据S阴影=S扇形AOD-S△AOD即可求解.解答:解:(1)∵AD∥BC,∠BAD=120°.∴∠ABC=60°.又∵BD平分∠ABC,∴∠ABD=∠DBC=∠ADB=30°∴==,∠BCD=60°∴AB=AD=DC,∠DBC=90°又在直角△BDC中,BC是圆的直径,BC=2DC.∴BC+BC=15∴BC=6∴此圆的半径为3.(2)设BC的中点为O,由(1)可知O即为圆心.连接OA,OD,过O作OE⊥AD于E.在直角△AOE中,∠AOE=30°∴OE=OA•cos30°=S△AOD=×3×=.∴点评:本题主要考查了扇形的面积的计算,正确证得四边形ABCD是等腰梯形,是解题的关键.例3、考点:圆与圆的位置关系;坐标与图形性质;扇形面积的计算分析:(1)根据题意作图即可求得答案,注意圆的半径为2;(2)首先根据题意求得扇形BP1A与△BP1A的面积,再作差即可求得劣弧错误!未找到引用源。与弦AB围成的图形的面积.解答:解:(1)如图:∴⊙P与⊙P1的位置关系是外切;
(2)如图:∠BP1A=90°,P1A=P1B=2,∴S扇形BP1A==π,S△AP1B=×2×2=2,∴劣弧与弦AB围成的图形的面积为:π﹣2.点评:此题考查了圆与圆的位置关系以及扇形面积的求解方法.题目难度不大,解题的关键是注意数形结合思想的应用.四、1、【解析】△ABC绕点C顺时针旋转60°,顶点A经过的路径是以C为圆心AC为半径,圆心角为60°的弧,根据弧长公式,可求路径长为【答案】C【点评】考查的知识点有网格中的勾股定理(求AC),图形的旋转,弧长公式。中等难度的题型。2、【解析】三角形的周长恰好是圆周长的三倍,但是圆在点A、B、C处分别旋转了一个角度,没有滚动,在三个顶点处旋转的角度之和是三角形的外角和360°。所以⊙O自转了4圈。【答案】C【点评】本题最容易出错的地方就是在顶点处的旋转,难度较大。如果学生能动手操作一下,正确答案就出来了。3、【解析】图中阴影部分的面积等于:三角形AOB面积-扇形AOB面积,不难知道,∆AOB为等边三角形,可求出∆AOB边AB上的高是,扇形AOB圆心角∠O=60°,半径OA=,从而阴影部分的面积是×2×-=,故选A.【答案】A【点评】本题着重考查了扇形面积的计算及解直角三角形的知识,以及转化、数形结合思想,有一定综合性,难度中等.
4、【解析】如下图所示,取AB与CD的交点为E,由垂径定理知CE=,而∠COB=2∠CDB=60°,所以OC==2,OE=OC=1,接下来发现OE=BE,可证△OCE≌△BED,所以S阴影=S扇形COB=π·22=.ABDCO图2E【答案】D【点评】圆的有关性质是中考高频考点,而图形面积也是多数地方必考之处,将它们结合可谓珠联璧合.解答此题需在多处转化:一是将阴影面积转化为扇形面积问题解决;二是由圆周角度数求出圆心角度数;三是发现图中存在的全等三角形,这一点是解题关键.5、【分析】S侧=πrl=π·×10=50π.【解答】50π【点评】圆锥的侧面积S侧=·2πr·l=πrl(其中r是圆锥底面圆的半径,l是母线的长).6、【解析】本题考查圆锥展开图及侧面积计算公式.设半径为r,圆锥侧面积即展开图扇形的面积,根据S扇=lR,即8π=×2π×4,得r=2.【答案】2【点评】在解决圆锥的计算问题时,要把握好两个相等关系:圆锥侧面展开图(扇形)的半径R等于圆锥的母线长,扇形的弧长等于圆锥的底面周长.几乎所有圆锥计算问题都是从这两个对应关系入手解决的.7、【解析】根据圆锥的侧面积公式=πrl计算,此圆锥的侧面积=π×2×5=10π【答案】10π【点评】本题综合考查有关扇形和圆锥的相关计算.解题思路:解决此类问题时要紧紧抓住两者之间的两个对应关系:①圆锥的母线长等于侧面展开图的扇形半径;②圆锥的底面周长等于侧面展开图的扇形弧长.正确对这两个关系的记忆是解题的关键.8、解析:圆锥的侧面积可由公式来求,这里R=6,l=8π,因此S=24π。答案:24π点评:本题考查了圆锥的侧面展开及其侧面积的求法,初步考查学生的空间观点,注意本题不要与全面积相混淆。9、分析:首先连接OB,由矩形的性质可得△BOC是直角三角形,又由OB=ON=2OC,∠BOC的度数,又由圆周角定理求得∠NMB的度数.解答:解:连接OB,∵CN=CO,∴OB=ON=2OC,∵四边形OABC是矩形,∴∠BCO=90°,∴cos∠BOC=,∴∠BOC=60°,∴∠NMB=∠BOC=30°.故答案为:30°.
点评:此题考查了圆周角定理、矩形的性质以及特殊角的三角函数值.此题难度适中,注意辅助线的作法,注意数形结合思想的应用.10、思路导引:确定路线长度,由于路线是圆弧,因此确定旋转角,与旋转半径是解决问题的关键,+;解析:计算斜边长度是2,第一次经过路线长度是,第二次经过路线长度是,第三次经过路线长度与第二次经过路线长度相同,也是,所以当点A三次落在直线l上时,经过的路线长度是+2×()=++2×=+点评:解答旋转问题,确定旋转中心、旋转半径以及旋转角度是前提,另外计算连续的弧长问题,注意旋转规律,进行多次循环旋转的有关弧长之和的计算.11、考点:圆锥的计算。专题:计算题。分析:算出围成圆锥的扇形的弧长,除以2π即为圆锥的底面半径,利用勾股定理即可求得圆锥的高.解答:解:围成圆锥的弧长为=4πcm,∴圆锥的底面半径为4π÷2π=2cm,∴圆锥的高为=1cm.故答案为1cm.点评:考查圆锥的计算;得到圆锥的底面半径是解决本题的突破点;用到的知识点为:圆锥的底面周长等于侧面展开图的弧长.12、解析:(1)由CA切⊙O于A,得∠A=90°,再结合∠C=45°,得∠B=45°.连接AD,则由直径AB=2,得∠ADB=90°.故BD=AB×cos45°=2×cos45°=;(2)运用代换得到阴影部分的面积等于△ACD的面积.解:(1)填;(2)由(1)得,AD=BD.
∴弓形BD的面积=弓形AD的面积,故阴影部分的面积=△ACD的面积.∵CD=AD=BD=,∴S△ACD=CD×AD=××=1,即阴影部分的面积是1.点评:本题主要考查了圆的性质,切线的性质,等腰直角三角形的性质以及割补法,解法较多,有利于考生从自己的角度获取解题方法,中等偏下难度.13、【解析】(1)根据相等的弧长对应的圆周角相等,得∠ABC=∠D=60°。(2)直径对应的圆周角为直角,则由三角形内角和为180°,得出∠BAC的大小,继而得出∠BAE的大小为90°,即AE是⊙O的切线。(3)由题意易知,△OBC是等边三角形,则由劣弧AC对应的圆心角可求出劣弧AC的长。20.解:(1)∵∠ABC与∠D都是弧AC所对的圆周角∴∠ABC=∠D=60°…………2分(2)∵AB是⊙O的直径∴∠ACB=90°…………………………3分∴∠BAC=30°∴∠BAE=∠BAC+∠EAC=30°+60°=90°…………………4分即BA⊥AE∴AE是⊙O的切线…………………………………………………………5分OABCDE(3)如图,连结OC∵OB=OC,∠ABC=60°∴△OBC是等边三角形∴OB=BC=4,∠BOC=60°∴∠AOC=120°…………………7分∴劣弧AC的长为…………………………………………8分【点评】此题考查圆弧的长与其对应的圆心角、圆周角的关系,及三角形的内角和为180°。相等的弧长对应的圆周角、圆心角相等.14、【解析】阴影部分的周长包括线段AC+CD+DB的长和弧AB的长.由折叠的性质可知,AC+CD=OA=6;DB=OB=6.故周长可求.求面积需要连接OD,证明△ODB是正三角形,得到∠CBO=30°,求出OC的长,阴影部分的面积=-2.【答案】解:连接OD.∵OB=OD,OB=BD∴△ODB是等边三角形∠DBO=60°∴∠OBC=∠CBD=30°在Rt△OCB中,OC=OBtan30°=.∴∴有图可知,CD=OC,DB=OB弧AB+AC+CD+DB=2×6+6=12+6
【点评】此题考查了折叠的性质、扇形面积公式、弧长公式以及直角三角形的性质.此题难度适中,注意数形结合思想的应用,注意辅助线的作法.15、考点:垂径定理;勾股定理;直线与圆的位置关系;圆锥的计算;作图—复杂作图.分析:(1)根据叙述,利用正方形的网格即可作出坐标轴;(2)①利用(1)中所作的坐标系,即可表示出点的坐标;②在直角△OAD中,利用勾股定理即可求得半径长;③可以证得∠ADC=90°,利用扇形的面积公式即可求得扇形的面积;④利用切线的判定定理,证得∠DCE=90°即可.解答:解:(1)①建立平面直角坐标系②找出圆心(2)①C(6,2);D(2,0)②2错误!未找到引用源。③π(7分)④直线EC与⊙D相切 证CD2+CE2=DE2=25 (或通过相似证明)得∠DCE=90° ∴直线EC与⊙D相切.故答案为:①C(6,2);D(2,0)②2错误!未找到引用源。 ③π点评:本题主要考查了垂径定理,圆锥的计算,正确证明△DCE是直角三角形是难点.中考数学计算题专项训练一、集训一(代数计算)1.计算:
(1)(2)(3)2×(-5)+23-3÷(4)22+(-1)4+(-2)0-|-3|;(6)(8)(9)()0-()-2+tan45°(10) 2.计算:3.计算:4.计算:5.计算:二、集训二(分式化简)1..2。、3.(a+b)2+b(a﹣b).4.5.6、化简求值(1)÷,其中x=-5.(2)(a﹣1+)÷(a2+1),其中a=﹣1.(3),其中a=-1.(4),(5),并任选一个你喜欢的数a代入求值.(6)然后选取一个使原式有意义的的值代入求值
(7)8、化简9、化简求值:),其中m=.10、先化简,再求代数式的值,其中x=tan600-tan45011、化简:,其中12、化简并求值:,其中.13、计算:.14、先化简,再求值:·,其中x=-6.15、先化简:再求值:÷,其中a=2+.16、先化简,再求值:·÷,其中a为整数且-3<a<2.17、先化简,再求值:,其中,.18、先化简,再求值:,其中.19、先化简,再求值:,其中(tan45°-cos30°)20、.21、先化简再求值:,其中满足.22、先化简:,并从0,,2中选一个合适的数作为的值代入求值。
23、先化简,再求值:÷,其中x=224、化简:.25、先化简,再求值:,其中x=-3.三、集训三(求解方程)1.解方程x2﹣4x+1=0.2。解分式方程3.解方程:=.4。已知|a﹣1|+=0,求方裎+bx=1的解.5.解方程:x2+4x-2=06。解方程:-=2.四、集训四(解不等式)1.解不等式组,并写出不等式组的整数解.2.解不等式组3.解不等式组:4.解不等式组5.解方程组,并求的值.6.解不等式组7.解不等式组并把解集在数轴上表示出来。8.解不等式组:9.解不等式组,并写出整数解.五、集训五(综合演练)1、(1)计算:||;(2)先化简,再求值:,其中.
2、解方程:3、解不等式组4、(1);(2)5、(1)︳-3︱---+(3-π)0(2)(-2010)0+-2sin60°(2)先化简,再求值.,其中x=3..(3)已知x2-2x=1,求(x-1)(3x+1)-(x+1)2的值.6.先化简,再求值:,其中7.先化简,再求值:,其中.8.解分式方程:.9.解方程组:10.(1)计算:(-1)2+tan60°-(π+2010)012、已知a、b互为相反数,并且,则.13、已知那么x-y的值是()14、若不等式组的解集是,求的值15、计算:16、计算:+tan60°一.解答题(共30小题)1.计算题:①;②解方程:.2.计算:+(π﹣2013)0. 3.计算:|1﹣|﹣2cos30°+(﹣)0×(﹣1)2013.
4.计算:﹣. 5.计算:.6.. 7.计算:. 8.计算:.9.计算:. 10.计算:. 11.计算:.12..13.计算:. 14.计算:﹣(π﹣3.14)0+|﹣3|+(﹣1)2013+tan45°. 15.计算:.16.计算或化简:(1)计算2﹣1﹣tan60°+(π﹣2013)0+|﹣|.(2)(a﹣2)2+4(a﹣1)﹣(a+2)(a﹣2) 17.计算:(1)(﹣1)2013﹣|﹣7|+×0+()﹣1;(2).18.计算:. 19.(1)(2)解方程:.20.计算:(1)tan45°+sin230°﹣cos30°•tan60°+cos245°;(2).
21.(1)|﹣3|+16÷(﹣2)3+(2013﹣)0﹣tan60°(2)解方程:=﹣.22.(1)计算:.(2)求不等式组的整数解.23.(1)计算:(2)先化简,再求值:(﹣)÷,其中x=+1.24.(1)计算:tan30°(2)解方程:.25.计算:(1)(2)先化简,再求值:÷+,其中x=2+1.26.(1)计算:;(2)解方程:.27.计算:.28.计算:.29.计算:(1+)2013﹣2(1+)2012﹣4(1+)2011.30.计算:.中考数学基础题1一、选择题:下面各题均有四个选项,其中只有一个是符合题意的。每小题3分,共30分.)1.四个数-3.14,0,1,2中为负数的是()(A)-3.14(B)0(C)1(D)22.在下列四个图案中,不是中心对称图形的是()
3.2015年初,一列CRH5型高速车组进行了“300000公里正线运营考核”.标志着中国高铁车从“中国制造”到“中国创新”的飞跃.将数300000用科学记数法表示为().A.3×106B.3×105C.0.3×106D.30×1044.左下图所示的几何体是由若干个大小相同的小立方块搭成,则这个几何体的左视图是()5.如图,AB∥CD,FE⊥DB,垂足为E,∠1=50°,则∠2的度数是( )A.60°B.50°C.40°D.30°6.两名同学进行了10次三级蛙跳测试,经计算,他们的平均成绩相同,若要比较这两名同学的成绩哪一位更稳定,通常还需要比较他们的成绩的()(A)众数(B)中位数(C)方差(D)以上都不对7.已知⊙O的半径是5,直线是⊙O的切线,在点O到直线的距离是()(A)2.5(B)3(C)5(D)108.不等式组的解集是()A.B.C.D.9.已知2是关于的方程的一个根,并且这个方程的两个根恰好是等腰三角形ABC的两条边长,则三角形ABC的周长为()(A)10(B)14(C)10或14(D)8或10
10.如图,Rt△AOB中,AB⊥OB,且AB=OB=3,设直线x=t截此三角形所得阴影部分的面积为S,则S与t之间的函数关系的图象为下列选项中的( )A.B.C.D.二、填空题(本题共6小题,每小题4分,共24分.)11.一个角的度数是20°,则它的补角的度数为.12.分解因式:=.13.已知一元二次方程x²+4x+a=0有两个实数根,则a的取值范围是.14.内角和与外角和相等的多边形的边数为 .15.如图,在一张正方形纸片上剪下一个半径为r的圆形和一个半径为R的扇形,使之恰好围成图中所示的圆锥,则R与r之间的关系是 .16.王宇用火柴棒摆成如图所示的三个“中”字形图案,依次规律,第n个“中”字形图案需要 根火柴棒.
第16题2018年中考数学基础题2班级:姓名:座号:评分:一、选择题:下面各题均有四个选项,其中只有一个是符合题意的。每小题3分,共30分.)1.4的平方根是( )A.2B.﹣2C.±2D.162.2015年广东省人口数超过105000000,将105000000这个数用科学记数法表示为( )A.0.105×109B.1.05×109C.1.05×108D.105×1063.化简÷的结果是( )A.mB.C.m﹣1D.4.下列图形中是轴对称图形,但不是中心对称图形的是( )A.B.C.D.5.已知点P(﹣1,4)在反比例函数的图象上,则k的值是( )A.B.C.4D.﹣46.如图所示的几何体是由七个相同的小正方体组合而成的,它的俯视图是( )A.B.C.D.7.如图,在菱形ABCD中,AB=5,∠BCD=120°,则对角线AC等于( )第7题A.20B.15C.10D.58.小红上学要经过两个十字路口,每个路口遇到红、绿灯的机会都相同,小红希望上学时经过每个路口都是绿灯,但实际这样的机会是( )A.B.C.D.
9.如图,△ABC为⊙O的内接三角形,∠BOC=80°,则∠A等于( ) A.80°B.60°C.50°D.第9题40°10.如图,在平行四边形ABCD中,AD=8,点E,F分别是BD,CD的中点,则EF等于( )A.2B.3C.4D.5二、填空题(本题共6小题,每小题4分,共24分)11.把多项式2x2﹣8分解因式得:2x2﹣8= .12.在函数y=中,自变量x的取值范围是 .13.某种品牌的手机经过四、五月份连续两次降价,每部售价由1000元降到了810元.则平均每月降价的百分率为.14.如果关于x的方程x2﹣2x+k=0(k为常数)有两个不相等的实数根,那么k的取值范围是 .15.不等式组的解集是 .16.矩形纸片ABCD中,AB=3cm,BC=4cm,现将纸片折叠压平,使A与C重合,设折痕为EF,则重叠部分△AEF的面积等于 .三、解答题(本题共3小题,每小题6分,共18分)17.计算:(﹣)-1﹣|﹣1|+2sin60°+(π﹣4)0.18.先化简,再求代数式的值,其中=.19.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方
第19题图格的边长均为1个单位长度).(1)请画出△A1B1C1,使△A1B1C1与△ABC关于x轴对称;(2)将△ABC绕点O逆时针旋转90°,画出旋转后得到的△A2B2C2,并直接写出点B旋转到点B2所经过的路径长.2018年中考数学基础题3班级:姓名:座号:评分:一、选择题:(每小题4分,共40分)下面各题均有四个选项,其中只有一个是符合题意的1.下列图形是中心对称图形而不是轴对称图形的是( )A.B.C.D.2.函数y=﹣x2﹣4x﹣3图象顶点坐标是( )A.(2,﹣1)B.(﹣2,1)C.(﹣2,﹣1)D.(2,1)3.二次函数y=3x2-1中一次项系数是()A.3B.1C.-1D.04.下列方程,是一元二次方程的是()A.x2+3x-1=0B.y2-5x=1C.2x+1=0D.+x2=15.将抛物线y=3x2平移而得到抛物线y=3(x+2)2-3,正确的方法是()A.先向左平移2个单位再向上平移3个单位;B.先向左平移2个单位再向下平移3个单位;C.先向右平移2个单位再向上平移3个单位;D.先向右平移2个单位再向下平移3个单位.
6.将方程x-4x-1=0的左边变成平方的形式是()A.(x-2)=1B.(x-4)=1C.(x-2)=5D.(x-1)=47.如图,AB和CD都是⊙0的直径,∠AOC=50°,则∠C的度数是()OBCDAA.20°B.25°C.30°D.50°(第7题图)(第8题图)8.如图,是的弦,半径于点且则的长为()A.B.C.D.9.若关于的一元二次方程有两个不相等的实数根,则的取值范围是().A.B.C.且≠1D.且≠110.直线y=ax+b与抛物线y=ax2+bx-ab在同一坐标系里的大致图象正确的是()二、填空题(每小题4分,共24分)11.已知点P1(a﹣1,1)和P2(2,b﹣1)关于原点对称,则(a+b)2015的值为 .12.关于x的方程(m-3)x-x=5是一元二次方程,则m=_________.13.方程(x﹣1)(x+2)=0的根是.14.一元二次方程有两个相等的实数根,则的值是.
15.如图,将△绕直角顶点顺时针旋转90°,得到△,若,则∠1的度数是。16.某小区2013年屋顶绿化面积为2250平方米,计划2015年屋顶绿化面积要达到3560平方米.如果每年屋顶绿化面积的增长率相同设为,那么所列的方程是_____.三、简答题(每小题6分,共36分)17.解方程:x﹣2=x(x﹣2)18化简:.19因式分解(1)(x﹣1)(x﹣3)+1.(2)(x2+4)2﹣16x2.(20).解方程组:21.计算:.2018年中考数学基础题4班级:姓名:评分:一、选择题:下面各题均有四个选项,其中只有一个是符合题意的。每小题3分,共30分.)1.有理数的绝对值为()
A. B. C. D.2.我们虽然把地球称为“水球”,但可利用淡水资源匮乏.我国淡水总量仅约为899000亿米3,用科学记数法表示这个数为() A.0.899×104亿米3B.8.99×105亿米3C.8.99×104亿米3D.89.9×104亿米33.下列物体中,俯视图为矩形的是().4.计算:=()A.3B.C.D.45.已知等腰三角形的一个底角等于30°,则这个等腰三角形的顶角等于()第6题A、150°B、120°C、75°D、30°6.如图,在菱形ABCD中,AB=3,∠ABC=60°,则对角线AC=( ).A.12B.9C.6D.3ACBDE第7题7.如图,直线AB∥CD,∠A=70°,∠C=40°,则∠E等于()A.30° B.40° C.60° D.70°8.袋子内有3个红球和2个蓝球,它们只有颜色上的区别,从袋子中随机地取出一个球,取出红球的概率是()A.B. C. D.9.点P(﹣2,1)关于x轴对称的点的坐标是( ) A(﹣2,﹣1)B.(2,﹣1)C.(2,1)D.(1,﹣2)10.二次函数的图象如图所示,则一次函数与反比例函数在同一平面直角坐标系中的大致图象为( )
ABCD二、填空题(本大题6小题,每小题4分,共24分)请将下列各题的正确答案填写在答题卡相应的位置上.第13题图11.分解因式:=______.12.已知正比例函数,点(2,﹣3)在函数上,则. 13.如图,AB为⊙O的直径,CD为⊙O的一条弦,CD⊥AB,垂足为E,已知CD=6,AE=1,则⊙O的半径为. 14.在学校艺术节文艺汇演中,甲、乙两个舞蹈队队员的身高的方差分别是S甲2=1.5,S乙2=2.5,那么身高更整齐的是队(填“甲”或“乙”).15.不等式组的解集是.16.如图,三个小正方形的边长都为1,则图中阴影部分面积的和是 _______ (结果保留π).三、解答题(一)(本大题3小题,每小题6分,共18分)17.计算:
2018年中考数学基础题5班级:姓名:座号:评分:一、选择题:下面各题均有四个选项,其中只有一个是符合题意的。每小题2分,共40分.)123456789101.﹣3的相反数是( ) A.B.C.3D.﹣32.(3分)在下列运算中,计算正确的是( ) A.a3•a2=a6B.a8÷a2=a4C.(a2)3=a6D.a2+a2=a43.在以下永洁环保、绿色食品、节能、绿色环保四个标志中,是轴对称图形是( ) A.B.C.D.4.如图所示几何体的正视图是( ) A.B.C.D.5.两个相似三角形的相似比是1:2,其中较小三角形的周长为6cm,则较大的三角形的周长为( ) A.3cmB.6cmC.9cmD.12cm6.数据5,7,5,8,6,13,5的中位数是( ) A.5B.6C.7D.87.5的相反数是()A.5B.C.
D.8.下列的值中能使式子有意义的是()A.B.C.D.9.吸烟有害健康.据中央电视台2012年5月30日报道,全世界每年因吸烟引起的疾病致死的人数大约为600万,数据600万用科学记数法表示为()A.B.C.D.10.下列运算正确的是()A.B.C.D.012A.120B.012C.120D.11.不等式的解集在数轴上表示正确的是()图1A.B.C.D.12.如图1的几何体的主视图是()13.下列说法不正确的是()A.选举中,人们通常最关心的数据是众数.B.从1、2、3、4、5中随机取一个数,取得奇数的可能性比较大.C.某游艺活动的中奖率是60%,说明参加该活动10次就有6次会获奖.ADBOCD.数据3、5、4、1、2的中位数是3.14.如图,△ABC内接于⊙O,AD是⊙O的直径,∠ABC=25°,则∠CAD的度数是()A.25°B.60°C.65°D.75°15.若菱形两条对角线的长分别为6和8,则这个菱形的周长为()A.20B.16C.12D.1016.如图,在△ABC中,DE∥BC,若,则的值为( )A.1:9B.1:8C. 1:4 D.1:2
17.如图,已知∠ABC=90°,AB=πr,AB=2BC,半径为r的⊙O从点A出发,沿A→B→C方向滚动到点C时停止.则在此运动过程中,圆心O运动的总路程为( ) A.2πrB.3πrC.D.18.一个圆锥的侧面积是底面积的3倍,则这个圆锥的侧面展开图的圆心角为( ) A.60°B.90°C.120°D.180°19.若实数a、b、c满足a+b+c=0,且a<b<c,则函数y=ax+c的图象可能是( ) A.B.C.D.20.如图,在△ABC中,AB=AC=5,CB=8,分别以AB、AC为直径作半圆,则图中阴影部分面积是( ) A.B.25π﹣24C.25π﹣12D.二、填空题(本题共10题,每小题3分,共30分)1.据中新社报道:2012年我国粮食产量将达到570000000000千克,用科学记数法表示这个粮食产量为 _________ 千克.2.若二次根式有意义,则x的取值范围是 .3.分解因式:2x2﹣4xy+2y2= _________ .
4.如图,边长为1的正方形网格中,点A、B、C在格点上,则sin∠CAB= .5.已知圆锥的底面直径和母线长都是10cm,则圆锥的侧面积为 .6.因式分解x3_=_.7.如图所示,直线a∥b,直线c与直线a,b分别相交于点A、点B,AM⊥b,垂足为点M,若∠l=58°,则∠2=___________.8.如图4,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=26,CD=24,那么第8题sin∠OCE=_.第7题图9.已知关于x的一元二次方程有两个不相等的实数根,则k的取值范围为.10.已知一次函数y=kx+b,当0≤x≤2时,对应的函数值y的取值范围是-4≤y≤8,则kb的值为三、解答题(本题共5题,每小题6分,共30分)1.(6分)计算:.
2.解不等式组:并把解集在数轴上表示出来.3.先化简,再求值:(1﹣)•,其中a=﹣1.4如图,点B、E、C、F在一条直线上,AB=DE,AC=DF,BE=CF.求证:∠A=∠D.5如图,△ABC中,∠BAC=90°,AD⊥BC,垂足为D.求作∠ABC的平分线,分别交AD,AC于P,Q两点;并证明AP=AQ.(要求:尺规作图,保留作图痕迹,不写作法)