北师大版数学中考专题复习与训练课件-第1篇 专项集训4圆的综合证明与计算

北师大版数学中考专题复习与训练课件-第1篇 专项集训4圆的综合证明与计算

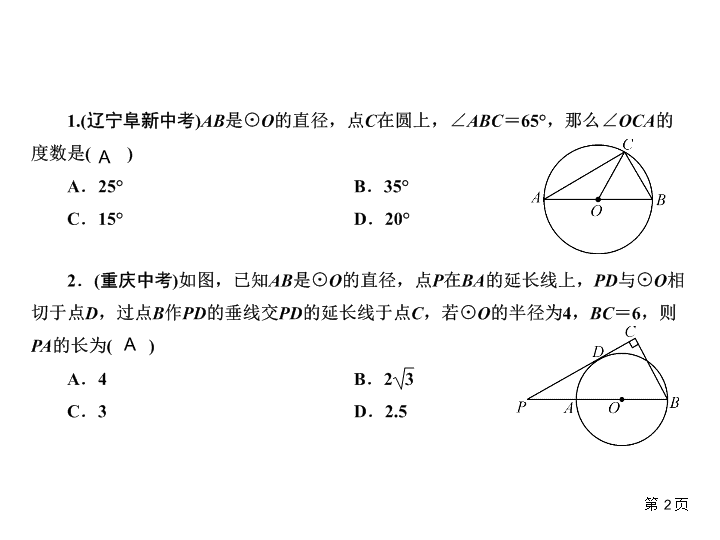
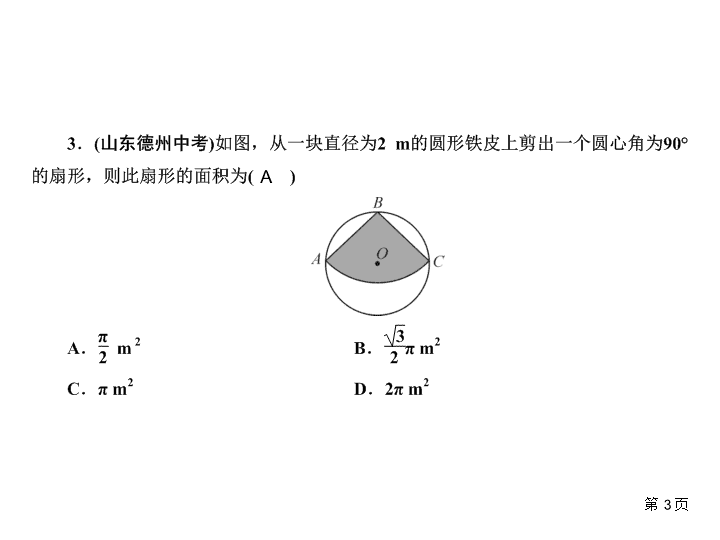
第一篇过教材·考点透析第六章　圆专项集训四　圆的综合证明与计算 第2页AA 第3页A 第4页A 5．(湖北荆门中考)如图，在平面直角坐标系xOy中，A(4,0)、B(0,3)、C(4,3)，I是△ABC的内心，将△ABC绕原点逆时针旋转90°后，I的对应点I′的坐标为()A．(－2,3)B．(－3,2)C．(3，－2)D．(2，－3)第5页A 6．(浙江台州中考)如图，等边三角形ABC边长是定值，点O是它的外心，过点O任意作一条直线分别交AB、BC于点D、E.将△BDE沿直线DE折叠，得到△B′DE，若B′D、B′E分别交AC于点F、G，连接OF、OG，则下列判断错误的是()A．△ADF≌△CGEB．△B′FG的周长是一个定值C．四边形FOEC的面积是一个定值D．四边形OGB′F的面积是一个定值第6页D 第7页B 8．(广西玉林中考)如图，大小不同的两个磁块，其截面都是等边三角形，小三角形边长是大三角形边长的一半，点O是小三角形的内心，现将小三角形沿着大三角形的边缘顺时针滚动，当由①位置滚动到④位置时，线段OA绕点O顺时针转过的角度是()A．240°B．360°C．480°D．540°第8页C 第9页 10．(2019·湖北鄂州中考)如图，在平面直角坐标系中，已知C(3,4)，以点C为圆心的圆与y轴相切，点A、B在x轴上，且OA＝OB，点P为⊙C上的动点，∠APB＝90°，则AB长度的最大值为________.第10页16 11．(浙江宁波中考)如图，正方形ABCD的边长为8，M是AB的中点，P是BC边上的动点，连接PM，以点P为圆心，PM长为半径作⊙P.当⊙P与正方形ABCD的边相切时，BP的长为____________.第11页 第12页 第13页 第14页①②④ 15．(2019·四川宜宾中考)如图，线段AB经过⊙O的圆心O，交⊙O于A、C两点，BC＝1，AD为⊙O的弦，连接BD，∠BAD＝∠ABD＝30°，连接DO并延长交⊙O于点E，连接BE交⊙O于点M.(1)求证：直线BD是⊙O的切线；(2)求⊙O的半径OD的长；(3)求线段BM的长．(1)证明：∵OA＝OD，∠A＝∠B＝30°，∴∠A＝∠ADO＝30°，∴∠DOB＝∠A＋∠ADO＝60°，∴∠ODB＝180°－∠DOB－∠ABD＝90°.又∵OD是半径，∴BD是⊙O的切线．第15页 第16页 16．(2019·四川雅安中考)如图，已知AB是⊙O的直径，AC、BC是⊙O的弦，OE∥AC交BC于E，过点B作⊙O的切线交OE的延长线于点D，连接DC并延长交BA的延长线于点F.(1)求证：DC是⊙O的切线；(2)若∠ABC＝30°，AB＝8，求线段CF的长．第17页 (1)证明：如图，连接OC．∵OE∥AC，∴∠1＝∠ACB．∵AB是⊙O的直径，∴∠1＝∠ACB＝90°，∴OD⊥BC．由垂径定理，得OD垂直平分BC，∴DB＝DC，∴∠DBE＝∠DCE.又∵OC＝OB，∴∠OBE＝∠OCE，∴∠DBO＝∠OCD．∵DB为⊙O的切线，OB是半径，∴∠DBO＝90°，∴∠OCD＝∠DBO＝90°，即OC⊥DC．∵OC是⊙O的半径，∴DC是⊙O的切线．第18页 第19页 第20页 第21页 第22页 第23页 19．(2019·四川攀枝花中考)如图1，有一个残缺的圆，请做出残缺圆的圆心O(保留作图痕迹，不写做法)．如图2，设AB是该残缺圆⊙O的直径，C是圆上一点，∠CAB的平分线AD交⊙O于点D，过点D作⊙O的切线交AC的延长线于点E.(1)求证：AE⊥DE；(2)若DE＝3，AC＝2，求残缺圆的半圆面积．第24页 第25页 第26页 第27页 第28页 第29页 第30页