北师大版数学中考专题复习与训练课件-第1篇 第4章 4等腰三角形与直角三角形

北师大版数学中考专题复习与训练课件-第1篇 第4章 4等腰三角形与直角三角形

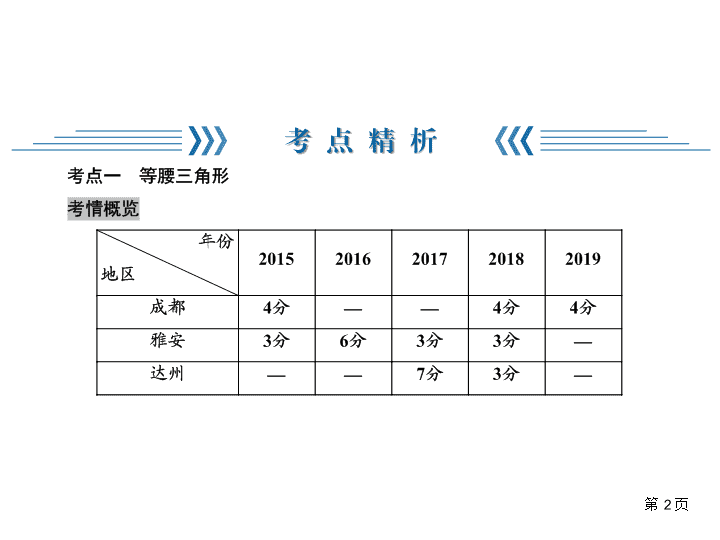
第一篇过教材·考点透析第四章　三角形4.3　等腰三角形与直角三角形 第2页考点精析 1．等腰三角形的判定(1)定义：在同一三角形中，有两条边①________的三角形是等腰三角形；(2)一个角的平分线与其对边上的中线、高互相重合的三角形是等腰三角形；(3)判定定理：在同一三角形中，如果两个角相等，那么这两个角所对的边也相等(简称：等角对②________)．第3页方法点拨：对于等腰直角三角形的判定，需判定它既是直角三角形又是等腰三角形．另外，等腰直角三角形具有直角三角形和等腰三角形的一切性质．相等等边 2．等腰三角形的性质(1)等边对③________，等腰三角形的两个底角④________.如图1，如果AB＝AC，那么可得∠B＝∠C．(2)三线合一：等腰三角形的顶角的平分线、底边上的中线、底边上的高互相⑤________.如图2，如果AB＝AC，AD平分∠BAC，那么可得AD⑥______BC，BD⑦______CD；如果AB＝AC，BD＝CD，那么可得AD⑧______BC，∠BAD⑨______∠CAD；如果AB＝AC，AD⊥BC，那么可得BD⑩______CD，∠BAD⑪______∠CAD．第4页等角相等重合⊥＝⊥＝＝＝ (3)等腰三角形是⑫__________图形，⑬______________________________________________________是它的对称轴．第5页方法点拨：以下两条性质，一般不直接作结论使用，但可以熟悉其内容，积累解题素材．(1)等腰三角形两底角的平分线相等，两条腰上的中线相等，两条腰上的高相等；(2)等腰三角形底边上任意一点到两腰距离之和等于一腰上的高(可用等面积法证明)．轴对称顶角平分线(底边上的中线、底边上的高)所在的直线 第6页 第7页方法点拨：等边三角形的四种判定方法都可以直接运用．解题时，要根据不同的条件进行选择，使问题简单化．三相等等腰60° 第8页相等60°重合3 第9页90°a2＋b2＝c2等于一半 第10页方法点拨：已知直角三角形中的两边求第三边(没有明确谁是斜边)时，一般要分：(1)所求边是斜边；(2)已知两边中的较长边是斜边进行讨论．余角等于等于一半30°一半 第11页 第12页四川中考真题精练AB 3．(2019·成都中考)如图，在△ABC中，AB＝AC，点D、E都在边BC上，∠BAD＝∠CAE，若BD＝9，则CE的长为______.4．(2015·成都中考)如图，直线m∥n，△ABC为等腰三角形，∠BAC＝90°，则∠1＝________度．第13页945 5．(2018·成都中考)等腰三角形的一个底角为50°，则它的顶角的度数为__________.6．(2019·广安中考)等腰三角形的两边长分别为6cm、13cm，其周长为________cm.7．(2018·甘孜、阿坝中考)直线上依次有A、B、C、D四个点，AD＝7，AB＝2，若AB、BC、CD可构成以BC为腰的等腰三角形，则BC的长为______________.第14页80°322或2.5 第15页 解：答案不唯一，如题图所示．第16页 9．(2017·内江中考)如图，AD平分∠BAC，AD⊥BD，垂足为点D，DE∥AC．求证：△BDE是等腰三角形．证明：如图，∵DE∥AC，∴∠1＝∠3.∵AD平分∠BAC，∴∠1＝∠2，∴∠2＝∠3.∵AD⊥BD，∴∠2＋∠B＝90°，∠3＋∠BDE＝90°，∴∠B＝∠BDE，∴△BDE是等腰三角形．第17页 第18页D 12．(2016·达州中考)如图，P是等边三角形ABC内一点，将线段AP绕点A顺时针旋转60°得到线段AQ，连结BQ.若PA＝6，PB＝8，PC＝10，则四边形APBQ的面积为______________.第19页 第20页A 第21页B 15．(2018·泸州中考)“赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲．如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形．设直角三角形较长直角边长为a，较短直角边长为b.若ab＝8，大正方形的面积为25，则小正方形的边长为()A．9B．6C．4D．3第22页D 16．(2017·德阳中考)如图，在△ABC中，AD是BC边上的高，BE平分∠ABC交AC边于点E，∠BAC＝60°，∠ABE＝25°，则∠DAC的大小是()A．15°B．20°C．25°D．30°第23页B 第24页D 18．(2019·宜宾中考)如图，已知直角△ABC中，CD是斜边AB上的高，AC＝4，BC＝3，则AD＝______.19．(2017·乐山中考)点A、B、C在格点图中的位置如图所示，格点小正方形的边长为1，则点C到线段AB所在直线的距离是______.第25页 20．(2019·浙江宁波中考)勾股定理是人类最伟大的科学发现之一，在我国古算书《周髀算经》中早有记载．如图1，以直角三角形的各边为边分别向外作正方形，再把较小的两张正方形纸片按图2的方式放置在最大正方形内．若知道图中阴影部分的面积，则一定能求出()A．直角三角形的面积B．最大正方形的面积C．较小两个正方形重叠部分的面积D．最大正方形与直角三角形的面积和第26页核心素养C 21．(湖南长沙中考)我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题目：“问有沙田一块，有三斜，其中小斜五里，中斜十二里，大斜十三里，欲知为田几何？”这道题讲的是：有一块三角形沙田，三条边长分别为5里，12里，13里，问这块沙田面积有多大？题中“里”是我国市制长度单位，1里＝500米，则该沙田的面积为()A．7.5平方千米B．15平方千米C．75平方千米D．750平方千米第27页A 22．(2019·浙江衢州中考)“三等分角”大约是在公元前五世纪由古希腊人提出来的，借助如图所示的“三等分角仪”能三等分任一角．这个三等分角仪由两根有槽的棒OA、OB组成，两根棒在O点相连并可绕O转动，C点固定，OC＝CD＝DE，点D、E可在槽中滑动．若∠BDE＝75°，则∠CDE的度数是()A．60°B．65°C．75°D．80°第28页D 突破点一　等腰三角形的性质(2019·山西中考)如图，在△ABC中，AB＝AC，∠A＝30°，直线a∥b，顶点C在直线b上，直线a交AB于点D，交AC于点E，若∠1＝145°，则∠2的度数是()A．30°B．35°C．40°D．45°第29页重难突破C 思路分析：∵AB＝AC，且∠A＝30°，∴∠ACB＝75°.在△ADE中，∵∠1＝∠A＋∠AED＝145°，∴∠AED＝145°－30°＝115°.∵a∥b，∴∠AED＝∠2＋∠ACB，∴∠2＝115°－75°＝40°，故选C．解题技巧：解答此题的关键是掌握等腰三角形的性质与平行线的性质．第30页 突破点二　等边三角形的性质(天津中考)如图，在边长为4的等边△ABC中，D、E分别为AB、BC的中点，EF⊥AC于点F，G为EF的中点，连接DG，则DG的长为______.第31页 第32页C 第33页 第34页D 第35页 第36页 (2019·黑龙江哈尔滨中考)在△ABC中，∠A＝50°，∠B＝30°，点D在AB边上，连接CD，若△ACD为直角三角形，则∠BCD的度数为______________.思路分析：因为当△ACD为直角三角形时，存在两种情况：∠ADC＝90°或∠ACD＝90°，所以需要分类讨论，再根据三角形的内角和定理得出结论．①如图1，当∠ADC＝90°时，∵∠B＝30°，∴∠BCD＝90°－30°＝60°.②如图2，当∠ACD＝90°时，∵∠A＝50°，∠B＝30°，∴∠ACB＝180°－30°－50°＝100°，∴∠BCD＝100°－90°＝10°，综上，∠BCD的度数为60°或10°.第37页60°或10° 解题技巧：本题考查了直角三角形的性质与三角形外角的性质，分情况讨论是本题的关键．第38页 第39页 解题技巧：解题的关键是用特殊到一般的方法探究规律，再利用规律解决问题．第40页 1．(2019·宁夏中考)如图，在△ABC中，AC＝BC，点D和E分别在AB和AC上，且AD＝AE.连接DE，过点A的直线GH与DE平行，若∠C＝40°，则∠GAD的度数为()A．40°B．45°C．55°D．70°第41页2020年迎考特训A双基过关C 2．(江苏扬州中考)在Rt△ABC中，∠ACB＝90°，CD⊥AB于点D，CE平分∠ACD交AB于点E，则下列结论一定成立的是()A．BC＝ECB．EC＝BEC．BC＝BED．AE＝EC3．(2019·湖北黄石中考)如图，在△ABC中，∠B＝50°，CD⊥AB于点D，∠BCD和∠BDC的平分线相交于点E，F为边AC的中点，CD＝CF，则∠ACD＋∠CED＝()A．125°B．145°C．175°D．190°第42页CC 5．(2019·湖南邵阳中考)公元3世纪初，中国古代数学家赵爽注《周髀算经》时，创造了“赵爽弦图”．如图，设勾a＝6，弦c＝10，则小正方形ABCD的面积是______.第43页4 6．(四川泸州中考)如图，等腰△ABC的底边BC＝20，面积为120，点F在边BC上，且BF＝3FC，EG是腰AC的垂直平分线，若点D在EG上运动，则△CDF周长的最小值为________.第44页1836 8．(广西桂林中考)如图，在△ABC中，∠A＝36°，AB＝AC，BD平分∠ABC，则图中等腰三角形的个数是______.第45页3 9．(吉林长春中考)如图1，这个图案是我国汉代的赵爽在注解《周髀算经》时给出的，人们称它为“赵爽弦图”．此图案的示意图如图2，其中四边形ABCD和四边形EFGH都是正方形，△ABF、△BCG、△CDH、△DAE是四个全等的直角三角形．若EF＝2，DE＝8，则AB的长为________.第46页10图1图2 10．(湖北黄冈中考)如图，圆柱形玻璃杯高为14cm，底面周长为32cm，在杯内壁离杯底5cm的点B处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿3cm与蜂蜜相对的点A处，则蚂蚁从外壁A处到内壁B处的最短距离为________cm.(杯壁厚度不计)第47页20 第48页 第49页 第50页B满分过关C 13．(2019·四川自贡中考)如图，在由10个完全相同的正三角形构成的网格图中，∠α、∠β如图所示，则cos(α＋β)＝______.14．(江苏盐城中考)如图，在直角△ABC中，∠C＝90°，AC＝6，BC＝8，P、Q分别为边BC、AB上的两个动点，若要使△APQ是等腰三角形且△BPQ是直角三角形，则AQ＝__________.第51页 15．(黑龙江中考)如图，已知等边△ABC的边长是2，以BC边上的高AB1为边作等边三角形，得到第一个等边△AB1C1；再以等边△AB1C1的B1C1边上的高AB2为边作等边三角形，得到第二个等边△AB2C2；再以等边△AB2C2的B2C2边上的高AB3为边作等边三角形，得到第三个等边△AB3C3；…，记△B1CB2的面积为S1，△B2C1B3的面积为S2，△B3C2B4的面积为S3，如此下去，则Sn＝________________.第52页 16．(浙江绍兴中考)数学课上，张老师举了下面的例题：例1等腰三角形ABC中，∠A＝110°，求∠B的度数．(答案：35°)例2等腰三角形ABC中，∠A＝40°，求∠B的度数．(答案：40°或70°或100°)张老师启发同学们进行变式，小敏编了如下一题：变式　等腰三角形ABC中，∠A＝80°，求∠B的度数．(1)请你解答以上的变式题；(2)解(1)后，小敏发现，∠A的度数不同，得到∠B的度数的个数也可能不同．如果在等腰三角形ABC中，设∠A＝x°，当∠B有三个不同的度数时，请你探索x的取值范围．第53页 第54页