北师大版数学九年级上册同步课件-1第一章- 复习课

北师大版数学九年级上册同步课件-1第一章- 复习课

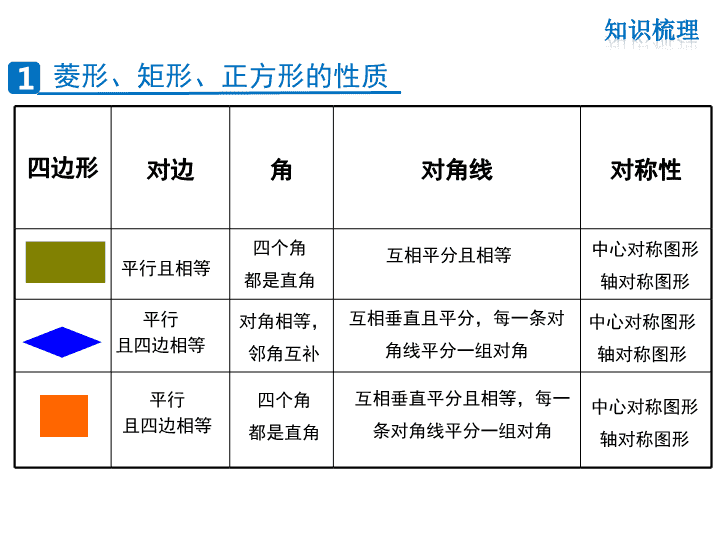
第一章特殊平行四边形复习课 四边形对边角对角线对称性平行且相等平行且四边相等平行且四边相等四个角都是直角对角相等，邻角互补四个角都是直角互相平分且相等互相垂直平分且相等，每一条对角线平分一组对角中心对称图形轴对称图形中心对称图形轴对称图形中心对称图形轴对称图形互相垂直且平分，每一条对角线平分一组对角菱形、矩形、正方形的性质知识梳理1 四边形条件①定义：有一外角是直角的平行四边形；②三个角是直角的四边形；③对角线相等的平行四边形①定义：一组邻边相等的平行四边形；②四条边都相等的四边形；③对角线互相垂直的平行四边形①定义：一组邻边相等且有一个角是直角的平行四边形；②有一组邻边相等的矩形；③有一个角是直角的菱形菱形、矩形、正方形的常用判定方法知识梳理2 如图，在菱形ABCD中，对角线AC与BD相交于点O，∠BAD=60°，BD=6，求菱形的边长AB.解：∵四边形ABCD是菱形，∴AB=AD(菱形的四条边相等）,∵∠BAD=60°，∴△ABD是等边三角形.∴AB=BD=6.ABCOD专题讲练例1菱形的性质和判定专题1 证明：在△AOB中.∵AB=,OA=2,OB=1.∴AB2=AO2+OB2.∴△AOB是直角三角形,且∠AOB=90°，∴AC⊥BD.∴□ABCD是菱形(对角线垂直的平行四边形是菱形).练习1：已知：如右图,在□ABCD中,对角线AC与BD相交于点O,AB=,OA=2,OB=1.求证：□ABCD是菱形.ABCOD专题讲练 2练习2：已知：如图,在△ABC中,AD是角平分线,点E、F分别在AB、AD上,且AE=AC,EF=ED.求证：四边形CDEF是菱形.ACBEDF证明：∵∠1=∠2,又∵AE=AC,AD是公共边,∴△ACD≌△AED(SAS).同理△ACF≌△AEF(SAS).∴CD=ED,CF=EF.又∵EF=ED,∴四边形ABCD是菱形（四边相等的四边形是菱形）.1专题讲练 练习3：如图，两张等宽的纸条交叉重叠在一起，猜想重叠部分的四边形ABCD是什么形状？说说你的理由.ABCDEF解：四边形ABCD是菱形.理由：过点C作AB边的垂线交于点E,作AD边上的垂线交于点F.S四边形ABCD=AD·CF=AB·CE.由题意可知CE=CF且四边形ABCD是平行四边形.∴AD=AB.∴四边形ABCD是菱形.专题讲练 解：∵四边形ABCD是矩形.∴AC=BD(矩形的对角线相等).OA=OC=AC,OB=OD=BD(矩形对角线相互平分),∴OA=OD.ABCDO专题讲练矩形的性质和判定如图,在矩形ABCD中,两条对角线相交于点O,∠AOD=120°,AB=2.5,求矩形对角线的长.例2专题2 ABCDO∵∠AOD=120°,∴∠ODA=∠OAD=(180°-120°)=30°.又∵∠DAB=90°（矩形的四个角都是直角）,∴BD=2AB=2×2.5=5.专题讲练 练习4：如图,在□ABCD中,对角线AC与BD相交于点O,△ABO是等边三角形,AB=4,求□ABCD的面积.解：∵四边形ABCD是平行四边形,∴OA=OC,OB=OD.又∵△ABO是等边三角形,∴OA=OB=AB=4,∠BAC=60°.∴AC=BD=2OA=2×4=8.ABCDO专题讲练 ∴□ABCD是矩形（对角线相等的平行四边形是矩形）.∴∠ABC=90°（矩形的四个角都是直角）.在Rt△ABC中,由勾股定理,得AB2+BC2=AC2,∴BC=.∴S□ABCD=AB·BC=4×=.ABCDO专题讲练 如图,在正方形ABCD中,E为CD上一点，F为BC边延长线上一点,且CE=CF.BE与DF之间有怎样的关系？请说明理由.解：BE=DF,且BE⊥DF.理由如下：（1）∵四边形ABCD是正方形.∴BC=DC,∠BCE=90°（正方形的四条边都相等,四个角都是直角）.∴∠DCF=180°-∠BCE=180°-90°=90°.ABDCFE正方形的性质和判定专题讲练例3专题3 ∴∠BCE=∠DCF.又∵CE=CF.∴△BCE≌△DCF.∴BE=DF.(2)延长BE交DF于点M,∵△BCE≌△DCF,∴∠CBE=∠CDF.∵∠DCF=90°,∴∠CDF+∠F=90°.∴∠CBE+∠F=90°,∴∠BMF=90°.∴BE⊥DF.ABDFECM专题讲练 练习5：如图,在矩形ABCD中,BE平分∠ABC,CE平分∠DCB,BF∥CE,CF∥BE.求证：四边形BECF是正方形.FABECD专题讲练 FABECD45°45°证明:∵BF∥CE,CF∥BE，∴四边形BECF是平行四边形.∵四边形ABCD是矩形,∴∠ABC=90°,∠DCB=90°,∵BE平分∠ABC,CE平分∠DCB,∴∠EBC=45°,∠ECB=45°,∴∠EBC=∠ECB.∴EB=EC,∴□BECF是菱形.在△EBC中∵∠EBC=45°,∠ECB=45°,∴∠BEC=90°,∴菱形BECF是正方形（有一个角是直角的菱形是正方形）.专题讲练 ★四边形的分类及转化有一个角是90°（或对角线互相垂直）有一对邻边相等（或对角线相等）平行四边形矩形菱形正方形一组邻边相等且一个内角为直角（或对角线互相垂直且相等）有一个角是90°（或对角线互相垂直）有一对邻边相等（或对角线相等）课堂小结