- 2021-11-06 发布 |
- 37.5 KB |
- 34页
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019年全国中考数学真题分类汇编:视图与尺规作图
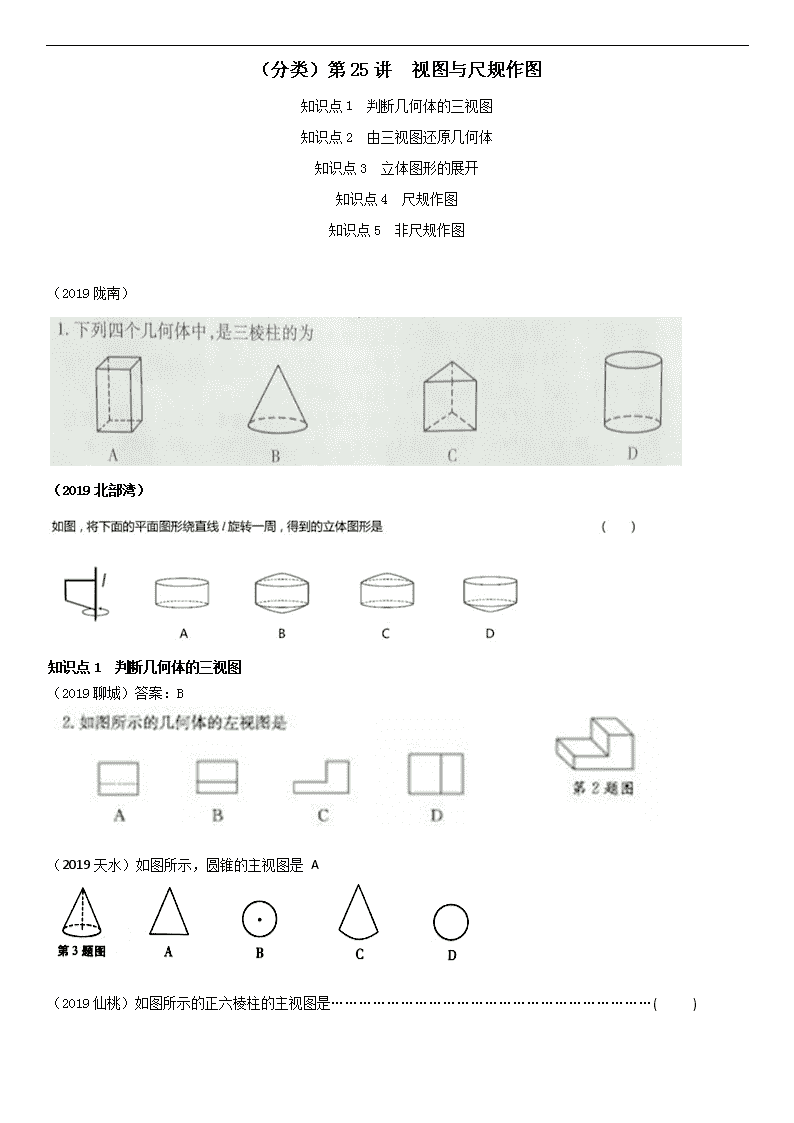
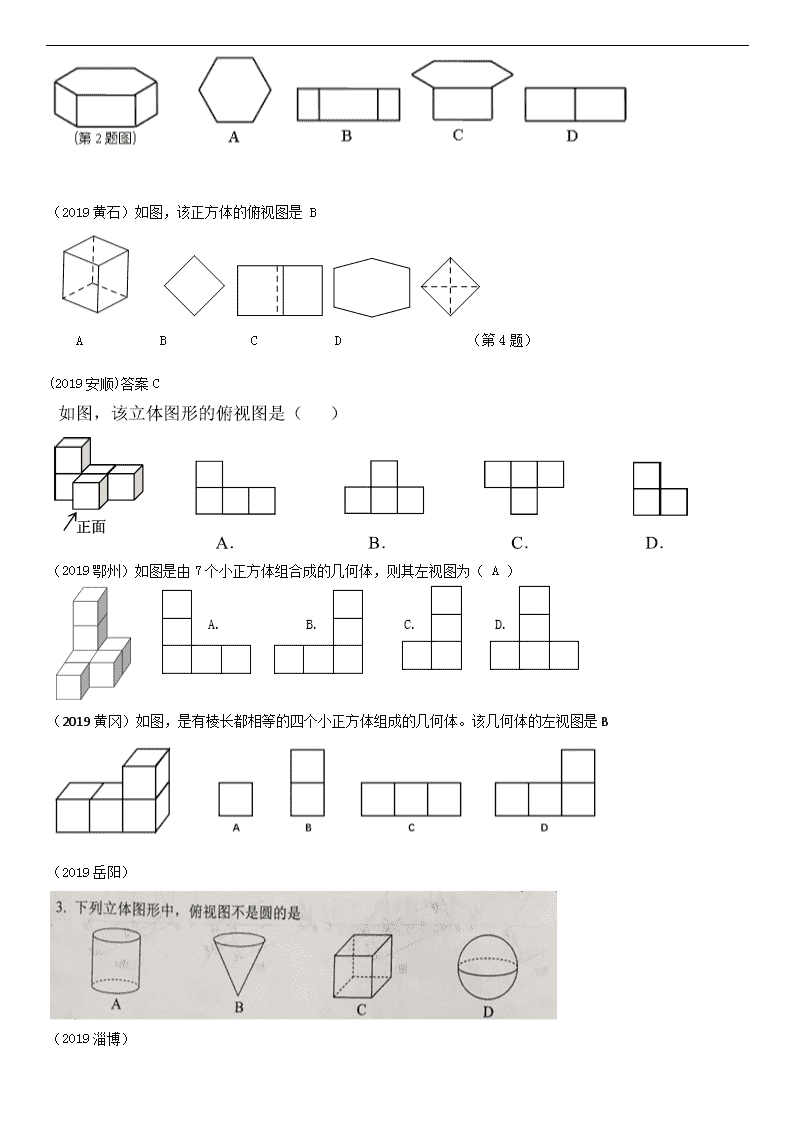
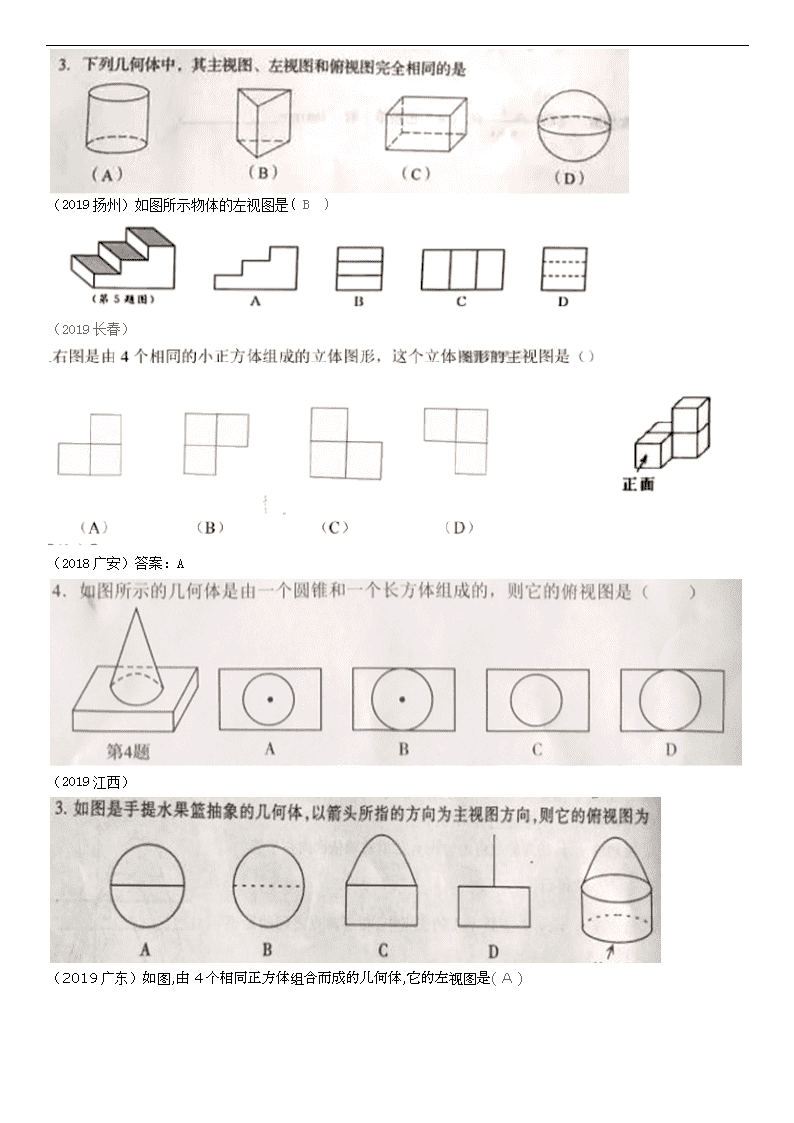
(分类)第25讲 视图与尺规作图 知识点1 判断几何体的三视图 知识点2 由三视图还原几何体 知识点3 立体图形的展开 知识点4 尺规作图 知识点5 非尺规作图 (2019陇南) (2019北部湾) 知识点1 判断几何体的三视图 (2019聊城)答案:B (2019天水)如图所示,圆锥的主视图是 A (2019仙桃)如图所示的正六棱柱的主视图是……………………………………………………………( ) (2019黄石)如图,该正方体的俯视图是 B A B C D (第4题) (2019安顺)答案C (2019鄂州)如图是由7个小正方体组合成的几何体,则其左视图为( A ) (2019黄冈)如图,是有棱长都相等的四个小正方体组成的几何体。该几何体的左视图是B (2019岳阳) (2019淄博) (2019扬州)如图所示物体的左视图是( B ) (2019长春) (2018广安)答案:A (2019江西) (2019广东)如图,由4个相同正方体组合而成的儿何体,它的左视图是( A ) (2019绥化) (2019咸宁)如图是由5个完全相同的小正方形搭成的几何体,如果将小正方体A放到小正方体B的正上方,则它的( A ) (A)主视图会发生改变 (B)俯视图会发生改变 (C)左视图会发生改变 (D)三种视图都会发生改变 (2019孝感)D (2019盐城) (2019烟台) (2019绍兴)如图的几何体由6个相同的小正方体搭成,它的主视图是( A ) (2019温州)某露天舞台如图所示,它的俯视图是(B) (2019宁波)如图,下列关于物体的主视图画法正确的是( C ) (2019天津)答案:B (2019河南) (2019绵阳)下列几何体中,主视图是三角形的是( C ) A. B. C. D. (2019玉林) (2019眉山)如图是由6个完全相同的小正方体组成的立体图形,它的左视图是( ) 第3题图 A B C D (2019常州) (2019湘西)下列立体图形中,主视图是圆的是 (2019海南) (2019十堰) (2019贵阳) (2019嘉兴)右图是由四个相同的小正方形组成的立体图形,它的俯视图为( B ) (2019滨州) (2019巴中)答案:C (2019潍坊) (2019广元) (2019威海) (2019临沂)如图所示,正三棱柱的左视图是( A ) (2019成都)如图所示的几何体是由6个大小相同的小立方块搭成,它的左视图是( B ) A. B. C. D. (2019柳州) (2019安徽)3.一个由圆柱和圆锥组成的几何体如图水平放置,它的俯视图是( C ) (2019重庆A卷)如图是由4个相同的小正方体组成的一个立体图形,其主视图是( A ) A. B. C. D. (2019龙东地区) (2019邵阳) (2019衢州)如图是由4个大小相同的立方体达成的几何体,这个几何体的主视图是( A ) (2019自贡)下图是一个水平放置的全封闭物体,则它的俯视图是( C ) (2019重庆B卷)如图是一个由5个相同正方体组成的立体图形,它的主视图是( D ) (2019宜昌)如图所示的几何体的主视图是( D ) (2019建设兵团) (2019泸州)下列立体图形中,俯视图是三角形的是( A ) (2019达州)答案:C (2019青岛)如图,一个正方体由 27 个大小相同的小立方块搭成,现从中取走若干个小立方块,得到一个新的几何体.若新几何体与原正方体的表面积相等,则最多可以取走 16 个小立方块. 知识点2 由三视图还原几何体 (2019河池) (2019菏泽) (2019贺州) (2019台州) (2019长沙)答案:D (2019无锡)一个几何体的主视图、左视图、俯视图都是长方形,这个几何体可能是( A ) A.长方体 B.四棱锥 C.三棱锥 D.圆锥 (2019荆州) (2019齐齐哈尔) (2019淮安) (2019宜宾) (2019金华)答案:D (2019贵港) (2019桂林) (2019随州) (2019郴州)已知某几何体的三视图如图,其中主视图和左视图都是腰长为 5,底边长为 4 的等腰 三角形,则该几何体的侧面展开图的面积是 .(结果保留 π ) (2019聊城)答案:120° 知识点3 立体图形的展开 (2019遂宁) (2019黔东南)某正方体的平面展开图如下,由此可知,原正方体“中”字所在面的对面的汉字是 A.国 B.的 C.中 D.梦 (2019襄阳)D (2019毕节) (2019山西) (2019资阳) (2019深圳)B (2019益阳) (2019攀枝花)如图是一个多面体的表面展开图,如果面F在前面,从左面看是面B,那么从上面看是面 .(填字母) (2018济宁)答案:B (2018南充)如图是一个几何体的表面展开图,这个几何体是( C ) A B C D (2019连云港)一个几何体的侧面展开图如图所示,则该几何体的底面是(B) (2019南京)无盖圆柱形杯子的展开图如图所示.将一根长为20 cm的细木筷斜放在该杯子内,木筷露在杯子外面的部分至少有 5 cm. 知识点4 尺规作图 (2019深圳) (2019河北) (2019海南) (2019安顺)C (2019东营)如图,在 Rt△ABC 中, ÐACB = 90°,分别以点 B 和点 C 为圆心,大于BC 的长为半径作弧,两弧相交于 D、E 两点,作直线 DE 交 AB 于点 F,交 BC 于点 G,连结 CF. 若 AC=3,CG=2,则 CF 的长为( A ) (2019建设兵团) (2019益阳) (2019郴州)如图,分别以线段 AB 的两端点 A,B 为圆心,大于 AB 长为半径画弧,在线段 AB的两侧分别交于点 E,F,作直线 EF 交 AB 于点 O.在直线 EF 上任取一点 P(不与 O重合),连接 PA,PB,则下列结论不一定成立的是 A.PA=PB B.OA=OB C.OP=OF D.PO⊥AB (2019贵阳) (2019长沙)答案:B (2019毕节) (2019襄阳) (2019河南) (2019长春) (2019黔东南)如右图,以△ABC的顶点B为圆心,BA长为半径画弧,交BC边于点D,连接AD.若∠B=40°,∠C=360°,则∠DAC的大小为 . (2019青岛)已知: ∠α,直线 l 及 l 上两点 A, B. 求作: Rt△ABC ,使点 C 在直线 l 的上方,且∠ABC=90°, ∠BAC=∠α. (2019孝感)通过如下尺规作图,能确定点D是BC边中点的是( A ) (2019烟台) (2019广西北部湾) (2019玉林) (2019荆州) (2019潍坊) (2019成都)如图,□ABCD的对角线AC与BD相交于点O,按以下步骤作图:①以点A为圆心,以任意长为半径作弧,分别交AO,AB于点M,N;②以点O为圆心,以AM长为半径作弧,交OC于点;③以点为圆心,以MN长为半径作弧,在∠COB内部交前面的弧于点;④过点作射线交BC于点E,若AB=8,则线段OE的长为 4 . (2019柳州) (2019达州) 解:(1)如图. (2). (2019贵港) (2019广东)如图,在△ABC中,点D是AB边上的一点. (1)请用尺规作图法,在△ABC内,求作∠ADE,使∠ADE=∠B,DE交AC于E;(不要求写作法,保留作图痕迹) (2)在(1)的条件下,若=2,求的值. 解:(1)如图所示 (2) ∵∠ADE=∠B ∴DEBC ∴△ADE≌△ABC ∴==2 (2019仙桃)请仅用无刻度的直尺完成下列画图,不写画法,保留画图痕迹. (1)如图①,四边形ABCD中,AB=AD,∠B=∠D,画出四边形ABCD的对称轴m; (2)如图②,四边形ABCD中,AD∥BC,∠A=∠D,画出BC边的垂直平分线n. (2019广州)如图10,⊙O的直径AB=10,弦AC=8,连接BC。 (1) 尺规作图:作弦CD,使CD=BC(点D不与B重合),连接AD;(保留作图痕迹,不写作法) (2) 在(1)所作的图中,求四边形ABCD的周长。 解(1)图略 (2) (2019德州)如图,∠BPD=120°,点A、C分别在射线PB、PD上,∠PAC=30°,AC=23. (1)用尺规在图中作一段劣弧,使得它在A、C两点分别与射线PB和PD相切.要求:写出作法,并保留作图痕迹; (2)根据(1)的作法,结合已有条件,请写出已知和求证,并证明; (3)求所得的劣弧与线段PA、PC围成的封闭图形的面积. (2019河池) (2019咸宁)在Rt△ABC中,∠C=90°,∠A=30°,D,E,F分别是AC,AB,BC的中点,连接ED,EF. (1) 求证:四边形DEFC是矩形; (2) 请用无刻度的直尺在图中作出∠ABC的平分线(保留作图痕迹,不写作法). (2019孝感)如图,Rt△ABC中,∠ACB=90°,一同学利用直尺和圆规完成如下操作: ①以点C为圆心,以CB为半径画弧,角AB于点G;分别以点G、B为圆心,以大于的长为半径画弧,两弧交点K,作射线CK; ②以点B为圆心,以适当的长为半径画弧,交BC于点M,交AB的延长线于点N;分别以点M、N为圆心,以大于MN的长为半径画弧,两弧交于点P,作直线BP交AC的延长线于点D,交射线CK于点E. 请你观察图形,根据操作结果解答下列问题; (1) 线段CD与CE的大小关系是 ☆ .(3分) (2) 过点D作DF⊥AB交AB的延长线于点F,若AC=12,BC=5,求tan∠DBF的值.(5分) (2019福建)如图,已知△ABC为和点A'. (1)以点A'为顶点求作△A'B'C',使△A'B'C'∽△ABC,S△A'B'C'=4S△ABC; (尺规作图,保留作图痕迹,不写作法) (2)设D、E、F分别是△ABC三边AB、BC、AC的中点,D'、E'、F'分别是你所作的△A'B'C'三边A'B'、B'C'、A'C'的中点,求证:△DEF∽△D'E'F'. (2)证明(略) (2019枣庄)如图,BD是菱形ABCD的对角线,∠CBD=75°, (1)请用尺规作图法,作AB的垂直平分线EF,垂足为E,交AD于F;(不要求写作法,保留作图痕迹); (2)在(1)条件下,连接BF,求∠DBF的度数。 (2019盐城) (2019济宁) (2019陇南) (2019泰州) (2019无锡)按要求作图,不要求写作法,但要保留作图痕迹. (1)如图1,A为圆O上一点,请用直尺(不带刻度)和圆规作出得内接正方形; (2)我们知道,三角形具有性质,三边的垂直平分线相交于同一点,三条角平分线相交于一点,三条中线相交于一点,事实上,三角形还具有性质:三条高交于同一点,请运用上述性质,只用直尺(不带刻度)作图.①如图2,在□ABCD中,E为CD的中点,作BC的中点F;②图3,在由小正方形组成的网格中,的顶点都在小正方形的顶点上,作△ABC的高AH. (1)连结AE并延长交圆E于点C,作AC的中垂线交圆于点B,D,四边形ABCD即为所求 (2)①法一:连结AC,BD交于点O,连结EB交AC于点G,连结DG并延长交CB于点F, F即为所求 法二:连结AC,BD交于点O 连结EO并延长交AB于点G 连结GC,BE交于点M 连结OM并延长交CB于点F,F即为所求 ② (2019攀枝花)如图1,有一个残缺圆,请作出残缺圆的圆心O(保留作图痕迹,不写作法). 如图2,设AB是该残缺圆⊙O的直径,C是圆上一点,∠CAB的角平分线AD交⊙O于点D,过D作⊙O的切线交AC的延长线于点E. (1)求证:AE⊥DE; (2)若DE=3,AC=2,求残缺圆的半圆面积. (2019宿迁) (2019菏泽) 知识点5 非尺规作图 (2019江西)查看更多