- 2021-11-06 发布 |
- 37.5 KB |
- 26页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
鄂尔多斯专版2020中考数学复习方案第一单元数与式第02课时整式与因式分解课件
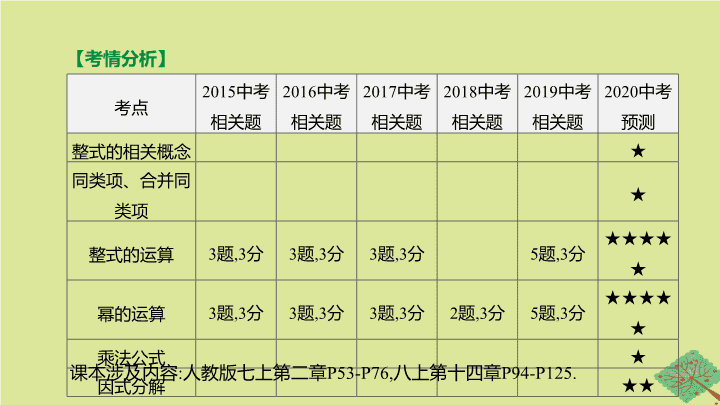
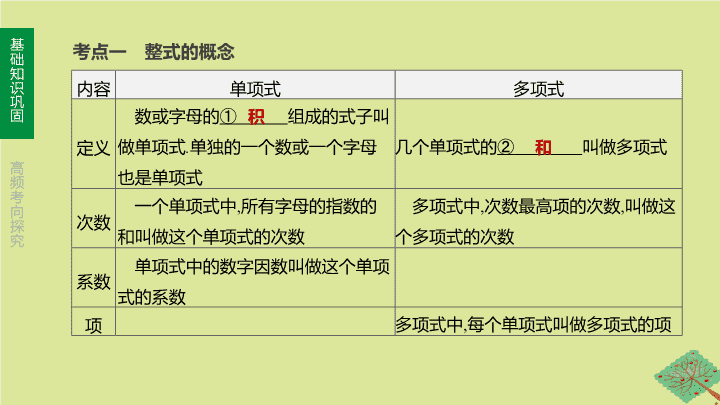
第 2 课时 整式与因式分解 第一单元 数与式 【 考情分析 】 考点 2015 中考 相关题 2016 中考 相关题 2017 中考 相关题 2018 中考 相关题 2019 中考 相关题 2020 中考预测 整式的相关概念 ★ 同类项、合并同类项 ★ 整式的运算 3 题 ,3 分 3 题 ,3 分 3 题 ,3 分 5 题 ,3 分 ★★★★★ 幂的运算 3 题 ,3 分 3 题 ,3 分 3 题 ,3 分 2 题 ,3 分 5 题 ,3 分 ★★★★★ 乘法公式 ★ 因式分解 ★★ 课本涉及内容 : 人教版七上第二章 P53-P76, 八上第十四章 P94-P125. 内容 单项式 多项式 定义 数或字母的 ① 组成的式子叫做单项式 . 单独的一个数或一个字母也是单项式 几 个单项式的 ② 叫做多项式 次数 一个单项式中 , 所有字母的指数的和叫做这个单项式的次数 多项式中 , 次数最高项的次数 , 叫做这个多项式的次数 系数 单项式中的数字因数叫做这个单项式的系数 项 多项式 中 , 每个单项式叫做多项式的项 考点一 整式的概念 积 和 1 . 同类项 : 所含字母 ③ , 并且相同字母的指数也 ④ 的项叫做同类项 . 几个常数项也是同类项 . 2 . 合并同类项 : 合并同类项后 , 所得项的系数是合并前各同类项的系数的和 , 且字母连同它的指数不变 . 考点二 同类项、合并同类项 相同 相同 【 温馨提示 】 (1) 同类项与系数无关 , 与字母的排列顺序无关 , 如 -7 xy 与 yx 是同类项 . (2) 只有同类项才能合并 , 如 x 2 与 x 3 不能合并 . 考点三 整式的运算 类别 法则 整式的 加减 整式的加减实质就是 ⑤ . 一般地 , 几个整式相加减 , 如果有括号就先去括号 , 然后再合并同类项 幂的 运算 同底数幂相乘 a m · a n = ⑥ ( m , n 都是整数 ) 幂的乘方 ( a m ) n = ⑦ ( m , n 都是整数 ) 合并同类项 a m + n a mn 类别 法则 幂的 运算 积的乘方 ( ab ) n = ⑧ ( n 为整数 ) 同底数幂相除 a m ÷a n = ⑨ ( a ≠0, m , n 都为整数 ) ( 续表 ) a n b n a m - n 类别 法则 整式的 乘法 单项式与单项式相乘 把它们的系数、同底数幂分别相乘 , 对于只在一个单项式里含有的字母 , 则连同它的指数作为积的一个因式 单项式与多项式相乘 m ( a + b + c )= ⑩ 多项式与多项式相乘 ( m + n )( a + b )= ⑪ ( 续表 ) ma + mb + mc ma + mb + na + nb 类别 法则 整式的 除法 单项式除以单项式 单项式除以单项式 , 把系数与同底数幂分别相除作为商的因式 , 对于只在被除式里含有的字母 , 则连同它的指数作为商的一个因式 多项式除以单项式 ( am + bm ) ÷m = a + b ( 续表 ) 类别 法则 乘法 公式 平方差公式 ( a + b )( a - b )= ⑫ 完全平方公式 ( a ± b ) 2 = ⑬ 常用恒 等变形 (1) a 2 + b 2 = ⑭ = ⑮ ; (2)( a - b ) 2 = ⑯ -4 ab ( 续表 ) a 2 - b 2 a 2 ±2 ab + b 2 ( a + b ) 2 -2 ab ( a - b ) 2 +2 ab ( a + b ) 2 考点四 因式分解 1 . 定义 : 把一个多项式化为几个整式的 ⑰ 的形式 , 这样的式子变形叫做这个多项式的因式分解 . 积 2 . 方法 (1) 提公因式法 (2) 公式法 3 . 步骤 一提 ( 提公因式 ); 二套 ( 套公式 ); 三检验 ( 检验是否分解彻底 ) . 考向一 整式的相关概念 5 考向二 同类项、合并同类项 3 . [2019· 毕节 ] 如果 3 ab 2 m -1 与 9 ab m +1 是同类项 , 那么 m 等于 ( ) A . 2 B . 1 C . -1 D . 0 A C [ 答案 ] 1 考向三 整式的运算 A B C D [ 答案 ] C [ 答案 ] 4 [ 解析 ]3 m +2 n =3 m ×3 2 n =3 m ×(3 2 ) n = 3 m ×9 n =2×2=4 . 11 . [2019· 乐山 ] 若 3 m =9 n =2, 则 3 m +2 n = . 考向四 因式分解 13 . [2014· 鄂尔多斯 11 题 ] 分解因式 : x 3 -4 xy 2 = . 14 . 分解因式 : (1) x 2 - xy = ; (2) x 2 -4= ; (3) x 2 -6 x +9= ; (4) ab 4 -4 ab 3 +4 ab 2 = . x ( x +2 y )( x -2 y ) x ( x - y ) ( x +2)( x -2) ( x -3) 2 ab 2 ( b -2) 2 考向五 创新题型 15 . [2019· 武汉 ] 观察等式 :2+2 2 =2 3 -2;2+2 2 +2 3 =2 4 -2;2+2 2 +2 3 +2 4 =2 5 -2;…; 已知按 一定规律排列的一组数 :2 50 ,2 51 ,2 52 ,…,2 99 ,2 100 , 若 2 50 = a , 用含 a 的式子表示这组数 的和是 ( ) A . 2 a 2 -2 a B . 2 a 2 -2 a -2 C . 2 a 2 - a D . 2 a 2 + a [ 答案 ] C [ 解析 ] 设 y 1 =2+2 2 +…+2 100 , y 2 =2+2 2 +…+2 49 , ∴2 50 +2 51 +2 52 +…+2 99 +2 100 = y 1 - y 2 =(2+2 2 +…+2 100 )-(2+2 2 +…+2 49 )=(2 101 -2)-(2 50 -2) =2 101 -2-2 50 +2=2 101 -2 50 =2 50 (2 51 -1)=2 50 (2×2 50 -1) . ∵2 50 = a ,∴ 原式 = a (2 a -1)=2 a 2 - a. 故选 C . 16 . [2019· 自贡 ] 阅读下列材料 : 小明为了计算 1+2+ 2 2 +…+2 2017 +2 2018 的值 , 采用以下方法 : 设 S =1+2+2 2 +…+2 2017 +2 2018 ,① 则 2 S =2+2 2 +…+2 2018 +2 2019 . ② ②-① 得 ,2 S - S = S =2 2019 -1 . 请仿照小明的方法解决以下问题 : (1)1+2+2 2 +…+2 9 = ; (2)3+3 2 +…+3 10 = ; (3) 求 1+ a + a 2 +…+ a n 的和 ( a> 0, n 是正整数 , 请写出计算过程 ) . 解 :(1)2 10 -1 [ 解析 ] 令 S =1+2+2 2 +…+2 9 ,① 则 2 S =2+2 2 +…+2 10 ,② ②-① 得 ,2 S - S = S =2 10 -1 . 16 . [2019· 自贡 ] 阅读下列材料 : 小明为了计算 1+2+ 2 2 +…+2 2017 +2 2018 的值 , 采用以下方法 : 设 S =1+2+2 2 +…+2 2017 +2 2018 ,① 则 2 S =2+2 2 +…+2 2018 +2 2019 . ② ②-① 得 ,2 S - S = S =2 2019 -1 . 请仿照小明的方法解决以下问题 : (2)3+3 2 +…+3 10 = ; 16 . [2019· 自贡 ] 阅读下列材料 : 小明为了计算 1+2+2 2 +…+2 2017 +2 2018 的值 , 采用以下方法 : 设 S =1+2+2 2 +…+2 2017 +2 2018 ,① 则 2 S =2+2 2 +…+2 2018 +2 2019 . ② ②-① 得 ,2 S - S = S =2 2019 -1 . 请仿照小明的方法解决以下问题 : (3) 求 1+ a + a 2 +…+ a n 的和 ( a> 0, n 是正整数 , 请写出计算过程 ) .查看更多