呼和浩特专版2020中考数学复习方案第三单元函数及其图象第10课时一次函数的图象与性质课件
第
10
课时
一次函数的图象与性质
第三单元 函数及其图象
考点一 一次函数的概念
考点聚焦
1
.
一般地
,
形如
y=kx
(
k
是常数
,
k
≠0)
的函数
,
叫做正比例函数
,
其中
k
叫做比例系数
.
2
.
一般地
,
形如
y=kx
+
b
(
k
,
b
是常数
,
k
≠0)
的函数
,
叫做一次函数
.
当
b=
0
时
,
y=kx
+
b
即
y=kx
,
所以说正比例函数是一种特殊的一次函数
.
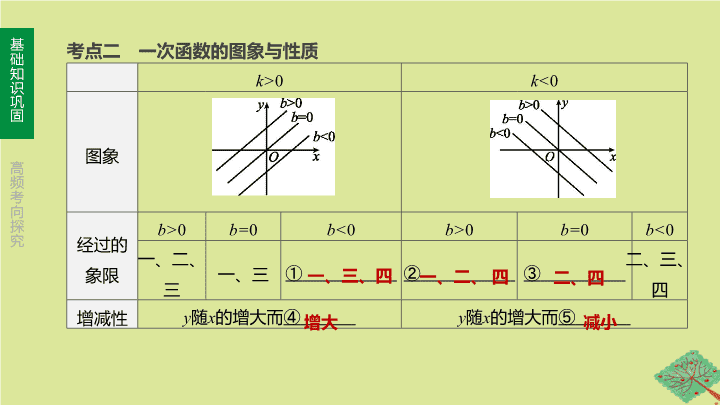
考点二 一次函数的图象与性质
k>
0
k<
0
图象
经过
的
象限
b>
0
b=
0
b<
0
b>
0
b=
0
b<
0
一、二、
三
一、三
①
②
③
二、三、
四
增减性
y
随
x
的增大
而
④
y
随
x
的增大
而
⑤
一、三、四
一、二、 四
二、四
增大
减小
(续表)
b
1
.
方法
:
待定系数法
2
.
步骤
:
(1)
设
:
设一般式
y=kx
+
b
(
k
≠0);
(2)
列
:
找出直线上两点的坐标
,
分别代入
y=kx
+
b
,
得到关于
k
,
b
的方程组
;
(3)
解
:
解方程组
,
求得
k
,
b
的值
;
(4)
依据
k
,
b
的值
,
写出一次函数的解析式
.
考点三 一次函数的解析式的确定
简记为
“
左加右减
,
上加下减
”(
左右平移只给
x
加减
,
上下平移等号右边整体加减
)
考点四 一次函数图象的平移
考点五 一次函数与一次方程
(
组
)
、一元一次不等式的关系
图
10-1
x
0
2
.
一次函数与不等式的关系
(1)
不等式
kx
+
b>
0(
kx
+
b<
0)
的解集
⇔
函数
y=kx
+
b
(
k
≠0)
的图象在
x
轴上方
(
下方
)
的部分对应的
x
的取值范围
⇔
函数
y=kx
+
b
(
k
≠0)
中
,
y
⑩
0
(
y
⑪
0)
时
x
的取值
;
(2)
如图
10-1,
不等式
k
1
x
+
b
1
>k
2
x
+
b
2
的解集是
x>m
;
不等式
k
1
x
+
b
1
≤
k
2
x
+
b
2
的解集是
⑫
.
>
<
x
≤
m
图
10-1
题组一 必会题
对点演练
1
.
如图
10-2,
直线
l
:
y=
-
x
-3
与直线
y=a
(
a
为常数
)
的交点在第四象限
,
则
a
的取值范围可能是
(
)
A
.
1
y
2
.
【
方法点析
】
在一次函数
y=kx
+
b
(
k
,
b
为常数
,
k
≠0)
中
,
k
和
b
的符号的作用
:
①
k
的符号决定增减性
,
当
k>
0
时
,
y
随
x
的增大而增大
,
当
k<
0
时
,
y
随
x
的增大而减小
;
②
b
的符号决定与
y
轴的交点在
x
轴的上方还是下方
(
上正、下负
),
特别地
,
当
b=
0
时
,
函数图象过原点
.
|
考向精练
|
1
.
两条直线
y
1
=ax
+
b
与
y
2
=bx
+
a
在同一坐标系中的图象可能是下图中的
(
)
图
10-4
[
答案
]A
[
解析
]
分四种情况讨论
.
若
a>
0,
b>
0,
则直线
y
1
与直线
y
2
均过第一、二、三象限
;
若
a>
0,
b<
0,
则直线
y
1
过第一、三、四象限
,
直线
y
2
过第一、二、四象限
;
若
a<
0,
b>
0,
则直线
y
1
过第一、二、四象限
,
直线
y
2
过第一、三、四象限
;
若
a<
0,
b<
0,
则直线
y
1
与直线
y
2
均过第二、三、四象限
.
故选
A
.
2
.
[2017·
呼和浩特
6
题
]
一次函数
y=kx
+
b
满足
kb>
0,
且
y
随
x
的增大而减小
,
则此函数的图象不经过
(
)
A
.
第一象限
B
.
第二象限
C
.
第三象限
D
.
第四象限
[
答案
]A
[
解析
]
由
“
y
随
x
的增大而减小
”
可知
k<
0,
又由
“
kb>
0”
得
b<
0,
所以图象经过第二、三、四象限
.
A
3
.
[2016·
呼和浩特
7
题
]
已知一次函数
y=kx
+
b
-
x
的图象与
x
轴的正半轴相交
,
且函数值
y
随自变量
x
的增大而增大
,
则
k
,
b
的取值情况为
(
)
A
.k>
1,
b<
0 B
.k>
1,
b>
0
C
.k>
0,
b>
0 D
.k>
0,
b<
0
考向二 一次函数解析式的确定
解
:(1)
∵图象平行于直线
y=
2
x
-1,
∴
k=
2
.
设函数解析式为
y=
2
x
+
b
,
将
(1,3)
代入
,
得
3
=
2×1+
b
,
∴
b=
1,
∴
y=
2
x
+1
.
|
考向精练
|
1
.
[2019·
绍兴
]
若三点
(1,4),(2,7),(
a
,10)
在同一直线上
,
则
a
的值等于
(
)
A
.
-1 B
.
0
C
.
3 D
.
4
[
答案
]C
图
10-5
3
.
[2017·
通辽
]
如图
10-6,
将八个边长为
1
的小正方形摆放在平面直角坐标系中
,
若过原点的直线
l
将图形分成面积相等的两部分
,
则将直线
l
向右平移
3
个单位长度后所得直线
l'
的函数解析式为
.
图
10-6
考向三 一次函数与方程、不等式组的关系
图
10-7
x=
3
x>
3
x<
3
|
考向精练
|
B
2
.
[2012·
呼和浩特
7
题
]
下面四条直线
,
其中直线上每个点的坐标都是二元一次方程
x
-2
y=
2
的解的是
(
)
图
10-8
C
图
10-9
D
考向四 一次函数与几何综合题
|
考向精练
|
图
10-10
[
答案
]A
图
10-11
[
答案
]
y=x
+1
3
.
[2018·
呼和浩特一模
]
矩形
ABCD
中
,
AB=
6,
BC=
8,
点
P
从点
A
出发沿
A
→
B
→
C
→
D
的路线移动
,
到
D
点停止运动
.
设点
P
移动的路线长为
x
,△
PAD
与矩形
ABCD
不重叠的部分的面积为
y.
(1)
写出
y
与
x
之间的函数关系式
.
(2)
当
x
取何值时
,
y=
28?
并说明此时点
P
在矩形的哪条边上
.
3
.
[2018·
呼和浩特一模
]
矩形
ABCD
中
,
AB=
6,
BC=
8,
点
P
从点
A
出发沿
A
→
B
→
C
→
D
的路线移动
,
到
D
点停止运动
.
设点
P
移动的路线长为
x
,△
PAD
与矩形
ABCD
不重叠的部分的面积为
y.
(2)
当
x
取何值时
,
y=
28?
并说明此时点
P
在矩形的哪条边上
.
图
10-12
图
10-12
图
10-12