- 2021-11-06 发布 |
- 37.5 KB |
- 3页
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
九年级下册数学教案 2-5 第2课时 利用二次函数求方程的近似根1 北师大版
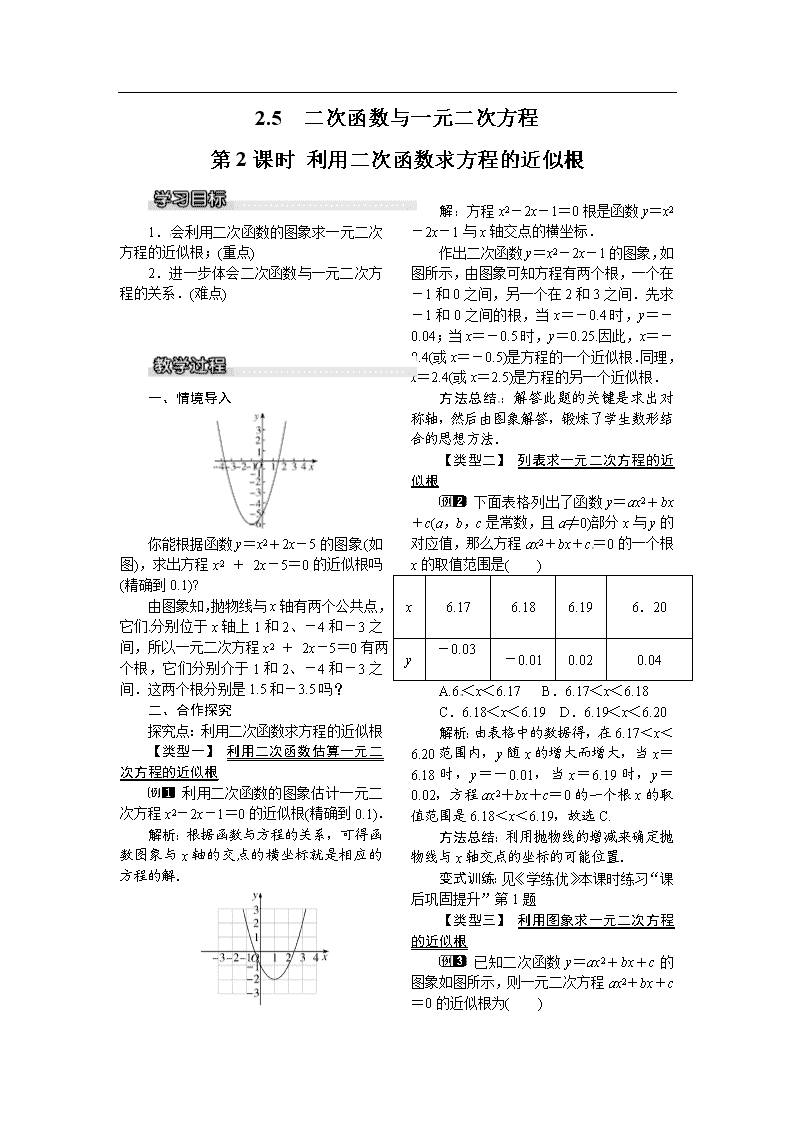
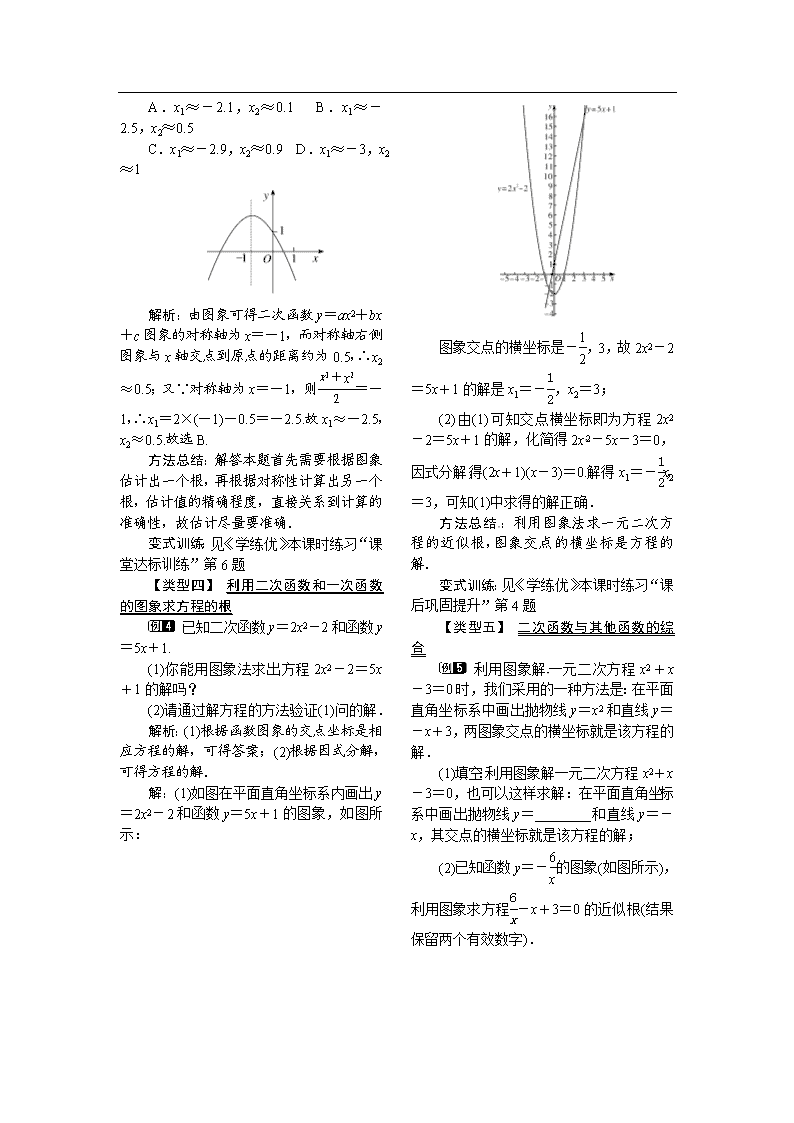
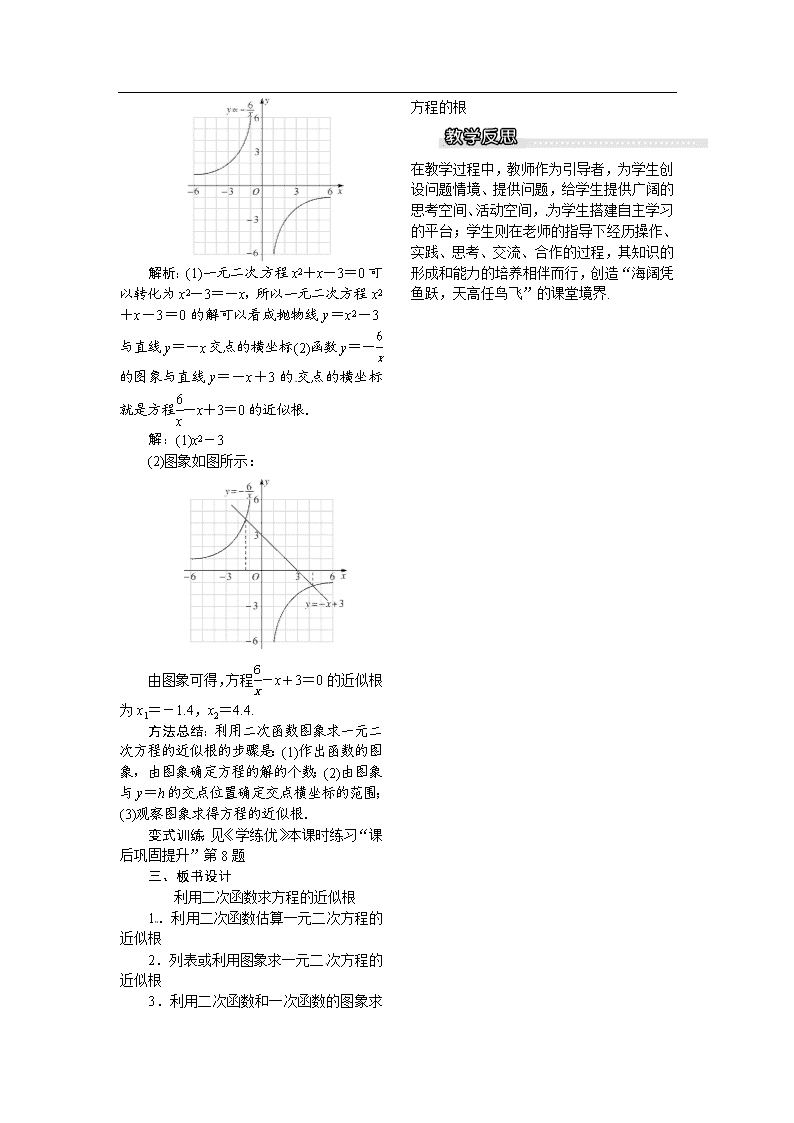
2.5 二次函数与一元二次方程 第2课时 利用二次函数求方程的近似根 1.会利用二次函数的图象求一元二次方程的近似根;(重点) 2.进一步体会二次函数与一元二次方程的关系.(难点) [来源:学。科。网Z。X。X。K] 一、情境导入 你能根据函数y=x2+2x-5的图象(如图),求出方程x2 + 2x-5=0的近似根吗(精确到0.1)? 由图象知,抛物线与x轴有两个公共点,它们分别位于x轴上1和2、-4和-3之间,所以一元二次方程x2 + 2x-5=0有两个根,它们分别介于1和2、-4和-3之间.这两个根分别是1.5和-3.5吗?[来源:Z,xx,k.Com] 二、合作探究 探究点:利用二次函数求方程的近似根 【类型一】 利用二次函数估算一元二次方程的近似根 利用二次函数的图象估计一元二次方程x2-2x-1=0的近似根(精确到0.1). 解析:根据函数与方程的关系,可得函数图象与x轴的交点的横坐标就是相应的方程的解. 解:方程x2-2x-1=0根是函数y=x2-2x-1与x轴交点的横坐标. 作出二次函数y=x2-2x-1的图象,如图所示,由图象可知方程有两个根,一个在-1和0之间,另一个在2和3之间.先求-1和0之间的根,当x=-0.4时,y=-0.04;当x=-0.5时,y=0.25.因此,x=-0.4(或x=-0.5)是方程的一个近似根.同理,x=2.4(或x=2.5)是方程的另一个近似根. 方法总结:解答此题的关键是求出对称轴,然后由图象解答,锻炼了学生数形结合的思想方法. 【类型二】 列表求一元二次方程的近似根[来源:Z,xx,k.Com] 下面表格列出了函数y=ax2+bx+c(a,b,c是常数,且a≠0)部分x与y的对应值,那么方程ax2+bx+c=0的一个根x的取值范围是( ) x 6.17 6.18 6.19 6.20 y -0.03[来源:Z_xx_k.Com] -0.01 0.02 0.04 A.6<x<6.17 B.6.17<x<6.18 C.6.18<x<6.19 D.6.19<x<6.20 解析:由表格中的数据得,在6.17<x<6.20范围内,y随x的增大而增大,当x=6.18时,y=-0.01,当x=6.19时,y=0.02,方程ax2+bx+c=0的一个根x的取值范围是6.18<x<6.19,故选C. 方法总结:利用抛物线的增减来确定抛物线与x轴交点的坐标的可能位置. 变式训练:见《学练优》本课时练习“课后巩固提升”第1题 【类型三】 利用图象求一元二次方程的近似根 已知二次函数y=ax2+bx+c的图象如图所示,则一元二次方程ax2+bx+c=0的近似根为( )[来源:学科网ZXXK] A.x1≈-2.1,x2≈0.1 B.x1≈-2.5,x2≈0.5 C.x1≈-2.9,x2≈0.9 D.x1≈-3,x2≈1 解析:由图象可得二次函数y=ax2+bx+c图象的对称轴为x=-1,而对称轴右侧图象与x轴交点到原点的距离约为0.5,∴x2≈0.5;又∵对称轴为x=-1,则=-1,∴x1=2×(-1)-0.5=-2.5.故x1≈-2.5,x2≈0.5.故选B. 方法总结:解答本题首先需要根据图象估计出一个根,再根据对称性计算出另一个根,估计值的精确程度,直接关系到计算的准确性,故估计尽量要准确. 变式训练:见《学练优》本课时练习“课堂达标训练”第6题 【类型四】 利用二次函数和一次函数的图象求方程的根 已知二次函数y=2x2-2和函数y=5x+1. (1)你能用图象法求出方程2x2-2=5x+1的解吗? (2)请通过解方程的方法验证(1)问的解. 解析:(1)根据函数图象的交点坐标是相应方程的解,可得答案;(2)根据因式分解,可得方程的解. 解:(1)如图在平面直角坐标系内画出y=2x2-2和函数y=5x+1的图象,如图所示: 图象交点的横坐标是-,3,故2x2-2=5x+1的解是x1=-,x2=3; (2)由(1)可知交点横坐标即为方程2x2-2=5x+1的解,化简得2x2-5x-3=0,因式分解,得(2x+1)(x-3)=0.解得x1=-,x2=3,可知(1)中求得的解正确. 方法总结:利用图象法求一元二次方程的近似根,图象交点的横坐标是方程的解. 变式训练:见《学练优》本课时练习“课后巩固提升”第4题 【类型五】 二次函数与其他函数的综合 利用图象解一元二次方程x2+x-3=0时,我们采用的一种方法是:在平面直角坐标系中画出抛物线y=x2和直线y=-x+3,两图象交点的横坐标就是该方程的解. (1)填空:利用图象解一元二次方程x2+x-3=0,也可以这样求解:在平面直角坐标系中画出抛物线y=________和直线y=-x,其交点的横坐标就是该方程的解; (2)已知函数y=-的图象(如图所示),利用图象求方程-x+3=0的近似根(结果保留两个有效数字). 解析:(1)一元二次方程x2+x-3=0可以转化为x2-3=-x,所以一元二次方程x2+x-3=0的解可以看成抛物线y=x2-3与直线y=-x交点的横坐标;(2)函数y=-的图象与直线y=-x+3的交点的横坐标就是方程-x+3=0的近似根. 解:(1)x2-3 (2)图象如图所示: 由图象可得,方程-x+3=0的近似根为x1=-1.4,x2=4.4. 方法总结:利用二次函数图象求一元二次方程的近似根的步骤是:(1)作出函数的图象,由图象确定方程的解的个数;(2)由图象与y=h的交点位置确定交点横坐标的范围;(3)观察图象求得方程的近似根. 变式训练:见《学练优》本课时练习“课后巩固提升”第8题 三、板书设计 利用二次函数求方程的近似根 1.利用二次函数估算一元二次方程的近似根 2.列表或利用图象求一元二次方程的近似根 3.利用二次函数和一次函数的图象求方程的根 在教学过程中,教师作为引导者,为学生创设问题情境、提供问题,给学生提供广阔的思考空间、活动空间,为学生搭建自主学习的平台;学生则在老师的指导下经历操作、实践、思考、交流、合作的过程,其知识的形成和能力的培养相伴而行,创造“海阔凭鱼跃,天高任鸟飞”的课堂境界.查看更多