2009年四川省南充市中考数学试卷（含答案）下载

2009年四川省南充市中考数学试卷（含答案）下载

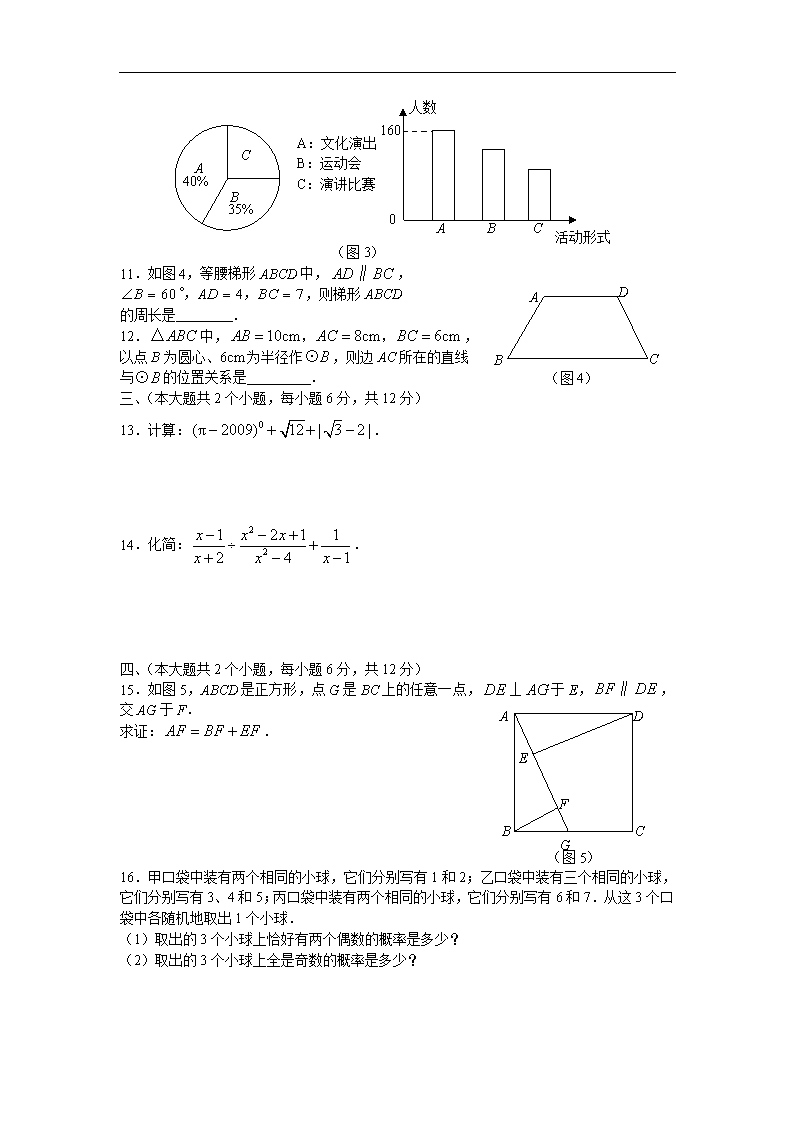
南充市二○○九年高中阶段学校招生统一考试 数 学 试 卷 ‎（满分100分，考试时间90分钟）‎ 一、细心选一选（本大题共8个小题，每小题3分，共24分）每小题下面都有代号为A、B、C、D的四个选项，其中只有一个选项是正确的，请把正确选项的代号填在该题后面的括号内．填写正确记3分，不填、填错或填出的代号超过一个均记0分．‎ ‎1．计算的结果是（ ）‎ A． B． C． D．‎ ‎2．在平面直角坐标系中，点与点B关于轴对称，则点B的坐标是（ ）‎ A． B． C． D．‎ ‎3．某物体的展开图如图1，它的左视图为（ ）‎ A．‎ B．‎ C．‎ D．‎ 图1‎ ‎4．方程的解是（ ）‎ A． B． C．或 D．或 ‎5．已知一组数据2，1，，7，3，5，3，2的众数是2，则这组数据的中位数是（ ）‎ A．2 B．‎2.5 ‎ C．3 D．5‎ ‎6．化简的结果是（ ）‎ ‎（图2）‎ O B D A C A． B． C． D．‎ ‎7．抛物线的对称轴是直线（ ）‎ A． B． C． D．‎ ‎8．如图2，AB是的直径，点C、D在上，，‎ ‎，则（ ）‎ A．70° B．60° C．50° D．40°‎ 二、认真填一填（本大题共4个小题，每小题3分，共12分）请将答案直接填写在题中横线上．‎ ‎9．不等式的解集是 ．‎ ‎10．某校为了举办“庆祝建国60周年”的活动，调查了本校所有学生，调查的结果如图3所示，根据图中给出的信息，这所学校赞成举办演讲比赛的学生有 人．‎ 活动形式 A B C 人数 ‎160‎ ‎0‎ ‎（图3）‎ A：文化演出 B：运动会 C：演讲比赛 C A B ‎40%‎ ‎35%‎ D C A B ‎（图4）‎ ‎11．如图4，等腰梯形ABCD中，，‎ ‎，则梯形ABCD 的周长是 ．‎ ‎12．中，，‎ 以点B为圆心、6cm为半径作，则边AC所在的直线 与的位置关系是 ．‎ 三、（本大题共2个小题，每小题6分，共12分）‎ ‎13．计算：．‎ ‎14．化简：．‎ 四、（本大题共2个小题，每小题6分，共12分）‎ ‎（图5）‎ D C B A E F G ‎15．如图5，ABCD是正方形，点G是BC上的任意一点，于E，，交AG于F．‎ 求证：．‎ ‎16．甲口袋中装有两个相同的小球，它们分别写有1和2；乙口袋中装有三个相同的小球，它们分别写有3、4和5；丙口袋中装有两个相同的小球，它们分别写有6和7．从这3个口袋中各随机地取出1个小球．‎ ‎（1）取出的3个小球上恰好有两个偶数的概率是多少？‎ ‎（2）取出的3个小球上全是奇数的概率是多少？‎ 五、（本大题共2个小题，每小题8分，共16分）‎ ‎17．在达成铁路复线工程中，某路段需要铺轨．先由甲工程队独做2天后，再由乙工程队独做3天刚好完成这项任务．已知乙工程队单独完成这项任务比甲工程队单独完成这项任务多用2天，求甲、乙工程队单独完成这项任务各需要多少天？‎ ‎18．如图6，在平面直角坐标系中，已知点，轴于A．‎ ‎（1）求的值；‎ ‎（2）将点B绕原点逆时针方向旋转90°后记作点，求点的坐标；‎ O x A B ‎1‎ ‎1‎ ‎（图6）‎ y ‎（3）将平移得到，点A的对应点是，点的对应点的坐标为，在坐标系中作出，并写出点、的坐标．‎ 六、（本大题8分）‎ ‎19．某电信公司给顾客提供了两种手机上网计费方式：‎ 方式A以每分钟0.1元的价格按上网时间计费；方式B除收月基费20元外，再以每分钟0.06元的价格按上网时间计费．假设顾客甲一个月手机上网的时间共有分钟，上网费用为元．‎ ‎10‎ ‎100‎ y/元 O ‎（图7）‎ x/分 ‎（1）分别写出顾客甲按A、B两种方式计费的上网费元与上网时间分钟之间的函数关系式，并在图7的坐标系中作出这两个函数的图象；‎ ‎（2）如何选择计费方式能使甲上网费更合算？‎ 七、（本大题8分）‎ ‎20．如图8，半圆的直径，点C在半圆上，．‎ ‎（1）求弦的长；‎ P B C E A ‎（图8）‎ ‎（2）若P为AB的中点，交于点E，求的长．‎ 八、（本大题8分）‎ ‎21．如图9，已知正比例函数和反比例函数的图象都经过点．‎ ‎（1）求正比例函数和反比例函数的解析式；‎ ‎（2）把直线OA向下平移后与反比例函数的图象交于点，求的值和这个一次函数的解析式；‎ ‎（3）第（2）问中的一次函数的图象与轴、轴分别交于C、D，求过A、B、D三点的二次函数的解析式；‎ y x O C D B A ‎3‎ ‎3‎ ‎6‎ ‎（4）在第（3）问的条件下，二次函数的图象上是否存在点E，使四边形OECD的面积与四边形OABD的面积S满足：？若存在，求点E的坐标；若不存在，请说明理由．‎ 南充市二○○九年高中阶段学校招生统一考试 数学试卷参考答案及评分意见 说明：‎ 1． 全卷满分100分，参考答案和评分意见所给分数表示考生正确完成当前步骤时应得的累加分数．‎ 2． 参考答案和评分意见仅是解答的一种，如果考生的解答与参考答案不同，只要正确就应该参照评分意见给分．合理精简解答步骤，其简化部分不影响评分．‎ 3． 要坚持每题评阅到底．如果考生解答过程发生错误，只要不降低后继部分的难度且后继部分再无新的错误，可得不超过后继部分应得分数的一半，如果发生第二次错误，后面部分不予得分；若是相对独立的得分点，其中一处错误不影响其它得分点的评分．‎ 一、细心选一选（本大题共8个小题，每小题3分，共24分）‎ ‎1．A 　 2．C 　 3．B 　 4．D 　 5．B 　 6．C 　 7．A 　 8．D 二、认真填一填（本大题共4个小题，每小题3分，共12分）‎ ‎9． 10．100 11．17 12．相切 三、（本大题共2个小题，每小题6分，共12分）‎ ‎13．解：原式 [共4分，分项给分：‎ ‎（1分），（1分），（2分）]‎ ‎ （结果正确，没有此步不扣分）‎ ‎ ． （6分）‎ ‎14．解：原式 （1分）‎ ‎ （3分）‎ ‎ （4分）‎ ‎ ‎ ‎ （5分）‎ ‎ （6分）‎ 四、（本大题共2个小题，每小题6分，共12分）‎ ‎15．证明：是正方形，‎ ‎． （1分）‎ ‎，‎ ‎．‎ ‎．‎ 又，‎ ‎． （2分）‎ ‎，‎ ‎． （3分）‎ 在与中，，‎ ‎． （4分）‎ ‎． （5分）‎ ‎，‎ ‎． （6分）‎ ‎16．解：根据题意，画出如下的“树形图”：‎ ‎6 7‎ ‎6 7‎ ‎6 7‎ ‎3‎ ‎4‎ ‎5‎ ‎1‎ ‎6 7‎ ‎6 7‎ ‎6 7‎ ‎3‎ ‎4‎ ‎5‎ ‎2‎ 甲 乙 丙 从树形图看出，所有可能出现的结果共有12个． （2分）‎ ‎（1）取出的3个小球上恰好有两个偶数的结果有4个，即1，4，6；2，3，6；2，4，7；2，5，6．所以 ‎（两个偶数）． （4分）‎ ‎（2）取出的3个小球上全是奇数的结果有2个，即1，3，7；1，5，7．所以 ‎（三个奇数）． （6分）‎ 五、（本大题共2个小题，每小题8分，共16分）‎ ‎17．解：设甲工程队单独完成任务需天，则乙工程队单独完成任务需天，‎ ‎ （1分）‎ 依题意得． （4分）‎ 化为整式方程得 ‎ （5分）‎ 解得或． （6分）‎ 检验：当和时，，‎ 和都是原分式方程的解．‎ 但不符合实际意义，故舍去； （7分）‎ 乙单独完成任务需要（天）．‎ 答：甲、乙工程队单独完成任务分别需要4天、6天． （8分）‎ O x A B ‎1‎ ‎1‎ y C D ‎18．解：（1）点，轴于，‎ ‎，‎ ‎． （3分）‎ ‎（2）如图，由旋转可知：，‎ 点的坐标是． （5分）‎ ‎（3）如图所示，‎ ‎，． （8分）‎ 六、（本大题8分）‎ ‎19．（1）方式A：， （1分）‎ 方式B：， （2分）‎ 两个函数的图象如图所示． （4分）‎ ‎10‎ ‎100‎ y/元 O x/分 ‎20‎ ‎50‎ ‎500‎ P 方式A 方式B ‎（2）解方程组 得 所以两图象交于点P（500，50）． （5分）‎ 由图象可知：当一个月内上网时间少于500分时，选择方式A省钱；当一个月内上网时间等于500分时，选择方式A、方式B一样；当一个月内上网时间多于500分时，选择方式B省钱． （8分）‎ 七、（本大题8分）‎ ‎20．解：是半圆的直径，点在半圆上，‎ ‎．‎ 在中， （3分）‎ ‎（2），‎ ‎．，‎ ‎．‎ 又，‎ ‎， （6分）‎ ‎ （7分）‎ ‎． （8分）‎ 八、（本大题8分）‎ ‎21．解：（1）设正比例函数的解析式为，‎ 因为的图象过点，所以 ‎，解得．‎ 这个正比例函数的解析式为． （1分）‎ 设反比例函数的解析式为．‎ 因为的图象过点，所以 ‎，解得．‎ 这个反比例函数的解析式为． （2分）‎ ‎（2）因为点在的图象上，所以 ‎，则点． （3分）‎ 设一次函数解析式为．‎ 因为的图象是由平移得到的，‎ 所以，即．‎ 又因为的图象过点，所以 ‎，解得，‎ 一次函数的解析式为． （4分）‎ ‎（3）因为的图象交轴于点，所以的坐标为．‎ 设二次函数的解析式为．‎ 因为的图象过点、、和，‎ 所以 （5分） 解得 这个二次函数的解析式为． （6分）‎ ‎（4）交轴于点，点的坐标是，‎ y x O C D B A ‎3‎ ‎3‎ ‎6‎ E 如图所示，‎ ‎．‎ 假设存在点，使．‎ 四边形的顶点只能在轴上方，，‎ ‎ ‎ ‎．‎ ‎，． （7分）‎ 在二次函数的图象上，‎ ‎．‎ 解得或．‎ 当时，点与点重合，这时不是四边形，故舍去，‎ 点的坐标为． （8分）‎