《同步课时卷》北师版八年级数学（下册）3

《同步课时卷》北师版八年级数学（下册）3

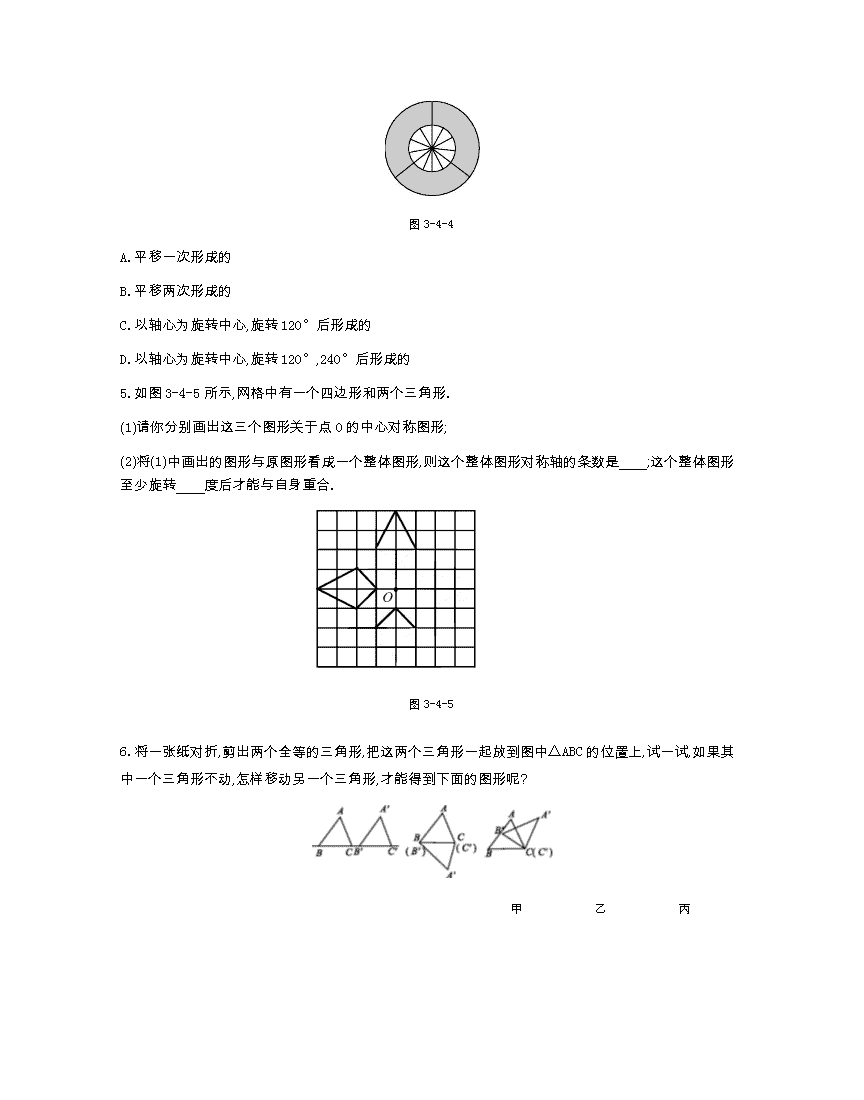
‎《同步课时卷》北师版八年级数学（下册）‎ ‎3.4简单的图案设计 ‎1.利用旋转分析图3-4-1所示的图案,请你设计一个你喜欢的徽标.‎ 图3-4-1‎ ‎2.请利用图3-4-2中的基本图案,通过平移、旋转、轴对称,在方格纸中设计一个美丽的图案.‎ 图3-4-2‎ ‎3.如图3-4-3所示,图案①可以看作是由图案②通过怎样变化得到的(　　)‎ ‎　　　　　　　　①　　　　　　　②‎ 图3-4-3‎ A.先按逆时针旋转90°再平移 B.先按逆时针旋转90°再作轴对称 C.先平移再作轴对称 D.先平移再逆时针旋转90°‎ ‎4.如图3-4-4是由三把相同大小的扇子展开后组成的图形,若把每把扇子的展开图看成“基本图案”,那么该图形是由“基本图案”(　　)‎ 图3-4-4‎ A.平移一次形成的 B.平移两次形成的 C.以轴心为旋转中心,旋转120°后形成的 D.以轴心为旋转中心,旋转120°,240°后形成的 ‎5.如图3-4-5所示,网格中有一个四边形和两个三角形.‎ ‎(1)请你分别画出这三个图形关于点O的中心对称图形;‎ ‎(2)将(1)中画出的图形与原图形看成一个整体图形,则这个整体图形对称轴的条数是　　;这个整体图形至少旋转　　度后才能与自身重合. ‎ 图3-4-5‎ ‎6.将一张纸对折,剪出两个全等的三角形,把这两个三角形一起放到图中△ABC的位置上,试一试,如果其中一个三角形不动,怎样移动另一个三角形,才能得到下面的图形呢?‎ ‎　　　　　 甲　　　　　　乙　　　　　　丙 ‎　　　　 丁　　　　　　　　戊 图3-4-6‎ 通过实际操作请回答下列问题:‎ ‎(1)这些图形中的两个三角形之间有什么样的关系?‎ ‎(2)在由△ABC变成△A’B’C’的过程中(只用一种变换),‎ ‎①经过轴对称的是　　　　. ‎ ‎②经过平移的是　　　　. ‎ ‎③经过旋转的是　　　　　. ‎ ‎7.将图3-4-7中的甲图案变为乙图案,需要用到哪些变换(　　)‎ 图3-4-7‎ A.旋转、平移 B.平移、轴对称 C.旋转、轴对称 D.旋转 ‎8.如图3-4-8①是3×3正方形方格,将其中两个方格涂黑,并且使涂黑后的整个图案是轴对称图形,约定绕正方形ABCD的中心旋转能重合的图案都视为同一种图案,例如图3-4-8②中的四幅图就视为同一种图案,则得到的不同图案共有(　　)‎ 图3-4-8‎ A.4种 B.5种 C.6种 D.7种 ‎9.如图3-4-9所示,图中图案可看作是以一个什么图案为“基础图形”形成的?试用两种方法分析它形成的过程.‎ 图3-4-9‎ ‎10.现有如图3-4-10①所示的两种瓷砖,请从这两种瓷砖中各选2块,拼成一个新的正方形地板图案,使拼铺的图案成轴对称图形或中心对称图形(如示例图②).‎ ‎(要求:分别在图③、图④中各设计一种与示例图不同的拼法,这两种拼法各不相同,且其中至少有一个既是轴对称图形,又是中心对称图形)‎ 图3-4-10‎ ‎11.将底边水平放置的等腰三角形沿底边的垂直平分线分别向上、向下平移1厘米,得到一组等腰三角形,连同垂直平分线形成的图案你能给出它的含义吗?将得到的图案作为“基本图案”,进行两次适当的平移,组成一组图案.这组图案又有什么意义呢?‎ 参考答案 ‎1.略.‎ ‎2.略.‎ ‎3.B ‎4.D ‎5.(1)‎ ‎(2)这个整体图形有4条对称轴,这个图形整体旋转90°后才能与自身重合.‎ ‎6.解:(1)根据平移、旋转及轴对称的性质可得:这些图形中的两个三角形全等.‎ ‎(2)①乙;②甲;③丙,丁,戊.‎ ‎7.A ‎8.C ‎9.解:如图3-4-9所示图形是由一个等腰三角形为基本图形,绕公共点顺时针(逆时针)依次旋转90°、180°、270°得到的;或者可以看作是由图形的左半部分,经过轴对称得到的.‎ ‎10.解:如图所示:两个图形既是轴对称图形,又是中心对称图形,答案不唯一.‎ ‎11.略.‎