北师大版八年级数学 上册 第三章三节 同步课时练习题（附参考答案）

北师大版八年级数学 上册 第三章三节 同步课时练习题（附参考答案）

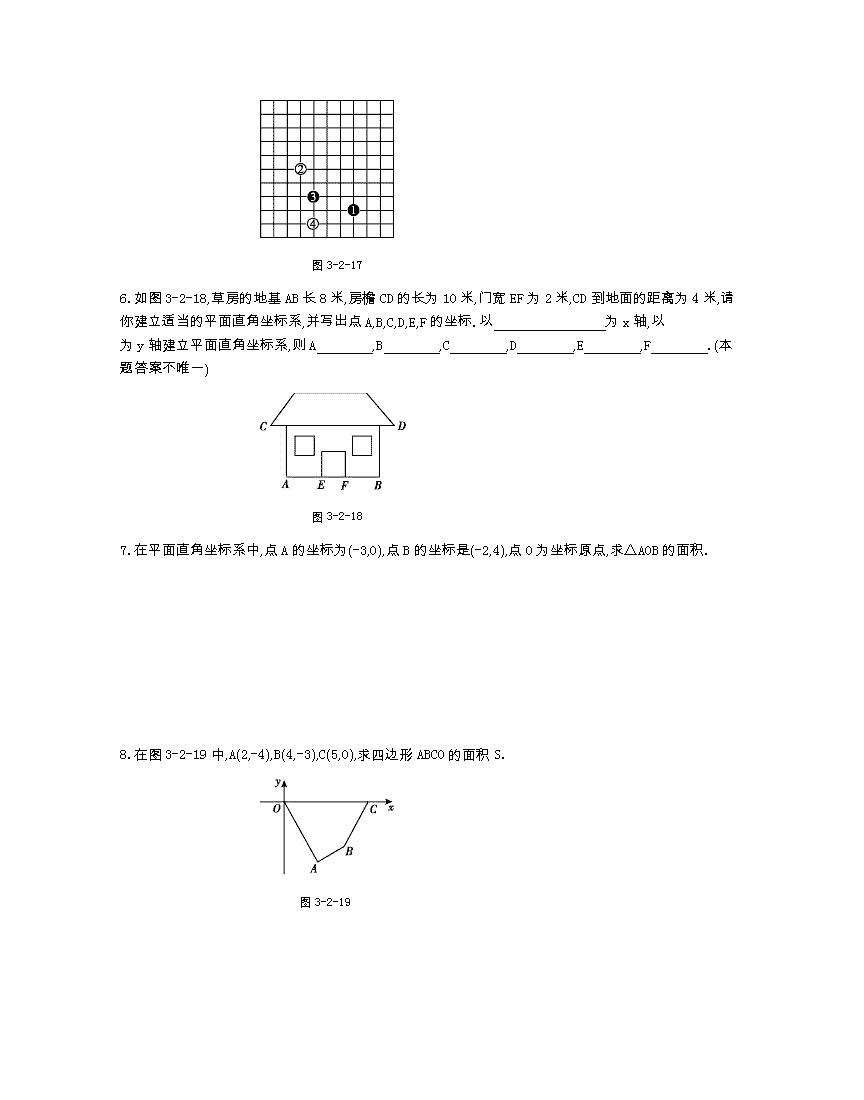
北师八上数学测试题第三章三节 ‎1.点A(3,-4)到y轴的距离为　　　　　　,到x轴的距离为　　　　　　,到原点的距离为　　　　　.‎ ‎2.如图3-2-15,若点E的坐标为(-2,1),点F的坐标为(1,-1),则点G的坐标为　　　　　　.‎ ‎　　　　　　　　　　‎ ‎　　　　　　　　　　　　　　　图3-2-15‎ ‎3.如图3-2-16,正方形ABCD的边长为3,用两种方法建立适当的直角坐标系,并写出各个顶点的坐标.‎ ‎　　　　　　　　　　‎ ‎　　　　　　　　　　　　　　　图3-2-16‎ ‎4.在平面直角坐标系中,A,B,C三点的坐标分别为(0,0),(0,-5),(-2,-2),以这三点为平行四边形的三个顶点,则第四个顶点不可能在第　　　　　　象限.‎ ‎5.如图3-2-17所示的围棋盘放置在某个平面直角坐标系内,白棋②的坐标为(-7,-4),白棋④的坐标为(-6,-8),那么黑棋①的坐标应该是　　　　　　　.‎ ‎　　　　　　　　　　‎ ‎　　　　　　　　　　　　　　　　图3-2-17‎ ‎6.如图3-2-18,草房的地基AB长8米,房檐CD的长为10米,门宽EF为2米,CD到地面的距离为4米,请你建立适当的平面直角坐标系,并写出点A,B,C,D,E,F的坐标.以　　　　　　　　为x轴,以　　　　　　　　　　　　　　　　为y轴建立平面直角坐标系,则A　　　　,B　　　　,C　　　　,D　　　　,E　　　　,F　　　　.(本题答案不唯一)‎ ‎　　　　　　　　　　‎ ‎　　　　　　　　　　　　　　　　图3-2-18‎ ‎7.在平面直角坐标系中,点A的坐标为(-3,0),点B的坐标是(-2,4),点O为坐标原点,求△AOB的面积.‎ ‎8.在图3-2-19中,A(2,-4),B(4,-3),C(5,0),求四边形ABCO的面积S.‎ ‎　　　　　　　　　　‎ ‎　　　　　　　　　　　　　　　图3-2-19‎ ‎9.如图3-2-20,一个长方形的两边长分别是8,4,建立直角坐标系,下列各点不在长方形上的是(　　)‎ ‎　　　　　　　　　　‎ ‎　　　　　　　　　　　　　　图3-2-20‎ A.(8,0)‎ B.(8,4)‎ C.(4,8)‎ D.(0,4)‎ ‎10.如图3-2-21,若在象棋盘上建立平面直角坐标系,使“帅”位于点(-1,-2),“马”位于点(2,-2),则“兵”位于点(　　)‎ ‎　　　　　　　　　　‎ ‎　　　　　　　　　　　　　　　　　　图3-2-21‎ A.(-1,1)‎ B.(-2,-1)‎ C.(-3,1)‎ D.(1,-2)‎ ‎11.如图3-2-22,等腰梯形ABCD的上底为4,下底为6,高为3.建立适当的平面直角坐标系,并写出各个顶点的坐标.‎ ‎　　　　　　　　　　‎ ‎　　　　　　　　　　　　　　图3-2-22‎ ‎12.如图3-2-23,是某学校的平面示意图.试建立平面直角坐标系,用坐标表示各建筑物的位置.‎ ‎　　　　　　　　　　‎ ‎　　　　　　　　　　　　　图3-2-23‎ ‎13.(1)关于x轴对称的两个点的坐标,　　　　　　　坐标相同,　　　　　　　坐标互为相反数.‎ ‎(2)关于y轴对称的两个点的坐标,　　　　　　　坐标相同,　　　　　　　坐标互为相反数.‎ ‎14.点A(-2,3)关于x轴的对称点A’的坐标为　　　　　　　.‎ ‎15.如图3-3-1,如果△A’B’C’与△ABC关于y轴对称,那么点A的对应点A’的坐标为　　　　　.‎ ‎　　　　　　　　　　‎ ‎　　　　　　　　　　　　　　　　　图3-3-1‎ ‎16.△ABC在平面直角坐标系中的位置如图3-3-2所示.‎ ‎(1)作出△ABC关于y轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;‎ ‎(2)作出△ABC关于x轴对称的△A2B2C2,并写出△A2B2C2各顶点的坐标.‎ ‎　　　　　　　　　　‎ ‎　　　　　　　　　　　　　　　　图3-3-2‎ ‎17.点A(2,4)关于x轴的对称点的坐标为　　　　　,点B(-3,-4)关于y轴的对称点的坐标为　　　　.‎ ‎18.已知点P(a,3),Q(-2,b)关于x轴对称,则a=　　　　　　,b=　　　　　　.‎ ‎19.如图3-3-3,上、下两幅“娃娃脸”图案关于x轴对称,上图中两只眼睛的坐标为(2.5,3),(3.5,3),则下图中两只眼睛的坐标分别是　　　　　　　　.‎ ‎　　　　　　　　　　‎ ‎　　　　　　　　　　　　　图3-3-3‎ ‎20.如图3-3-4.(1)将图中的各个点的纵坐标不变,横坐标都乘-1,与原图案相比,所得图案有什么变化?‎ ‎(2)将图中的各个点的横坐标不变,纵坐标都乘-1,与原图案相比,所得图案有什么变化?‎ ‎　　　　　　　　　　‎ ‎　　　　　　　　　　　　　　　图3-3-4‎ ‎21.如图3-3-5,在直角坐标系中,△AOB的顶点O和B的坐标分别是O(0,0),B(6,0),且∠OAB=90°,AO=AB,则顶点A关于x轴的对称点的坐标是(　　)‎ ‎　　　　　　　　　　‎ ‎　　　　　　　　　　　　　　图3-3-5‎ A.(3,3)‎ B.(-3,3)‎ C.(3,-3)‎ D.(-3,-3)‎ ‎22.如果点A(x+y,x)与点B(3,-1)关于x轴对称,那么(　　)‎ A.x=1,y=2‎ B.x=-1,y=-2‎ C.x=2,y=1‎ D.x=-2,y=-1‎ ‎23.如图3-3-6,在平面直角坐标系中,正方形ABCD的顶点坐标分别是A(1,1),B(1,-1),C(-1,-1),D(-1,1),y轴上有一点P(0,2),作P关于A的对称点P1,作P1关于B的对称点P2,作P2关于C的对称点P3,作P3关于D的对称点P4,作P4关于A的对称点P5……按此操作下去,则点P2 015的坐标为(　　)‎ ‎　　　　　　　　　　‎ ‎　　　　　　　　　　　　　　　　图3-3-6‎ A.(0,2)‎ B.(2,0)‎ C.(0,-2)‎ D.(-2,0)‎ ‎24.已知点P(a,b),它关于y轴的对称点是Q,且点Q关于x轴的对称点为R(-2,3),求a,b的值.‎ ‎25.在如图3-3-7所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).‎ ‎(1)请在如图所示的网格平面内作出平面直角坐标系;‎ ‎(2)请作出△ABC关于y轴对称的△A’B’C’;‎ ‎(3)写出点B’的坐标.‎ ‎　　　　　　　　　　‎ ‎　　　　　　　　　　　　　　　　　图3-3-7‎ 参考答案 ‎1.3　　　4　　　5‎ ‎2.(1,2)‎ ‎3.解:以点A为坐标原点,分别以AB,AD所在的直线为x轴、y轴建立直角坐标系.此时点A的坐标为(0,0).‎ 由正方形的边长为3,得AB=BC=CD=DA=3,所以B,C,D的坐标分别为B(3,0),C(3,3),D(0,3).其他方法略.‎ ‎4.一 ‎5.(-3,-7)‎ ‎6.AB所在直线　　　过EF中点,且与EF垂直的直线　　　(-4,0)　　　(4,0)　　　(-5,4)　　　(5,4)‎ ‎　　　(-1,0)　　　　(1,0)‎ ‎7.解:画图略.△AOB的面积是6.‎ ‎8.解:过点A,B分别作x轴的垂线,则S=×2×4+×(4+3)×2+×1×3=12.5.‎ ‎9.C ‎10.C ‎11.解:答案不唯一.如图所示: ‎ 以AB的中点O为原点,分别以AB所在直线和过O点的AB的垂线为x轴、y轴,建立平面直角坐标系,此时O(0,0),A(-3,0),B(3,0),D(-2,3),C(2,3).‎ ‎12.解:答案不唯一.如图所示: ‎ 当以旗杆为坐标中心建立平面直角坐标系时,各物体的位置分别为:旗杆(0,0),校门(-4,0),图书馆(-4,4),教学楼(-2,3),实验楼(-1,-3),餐厅(1,4),体育场(2,2),学生公寓(3,-3).‎ ‎13.(1)横　　　纵 ‎(2)纵　　　　横 ‎14.(-2,-3)‎ ‎15.(-1,3)‎ ‎16.解:(1)A1(0,4),B1(2,2),C1(1,1).图略.‎ ‎(2)A2(0,-4),B2(-2,-2),C(-1,-1).图略.‎ ‎17.(2,-4)　　　(3,-4)‎ ‎18.-2　　　-3‎ ‎19.(2.5,-3),(3.5,-3)‎ ‎20.解:(1)所得图案与原图案关于y轴对称;‎ ‎(2)所得图案与原图案关于x轴对称.‎ ‎21.C ‎22.A ‎23.D ‎24.解:由题意可知,点Q的坐标为(-2,-3),点P的坐标为(2,-3),所以a=2,b=-3.‎ ‎25.解:(1)(2)如图; ‎ ‎(3)点B’的坐标为(2,1).‎