- 2021-11-01 发布 |
- 37.5 KB |
- 12页
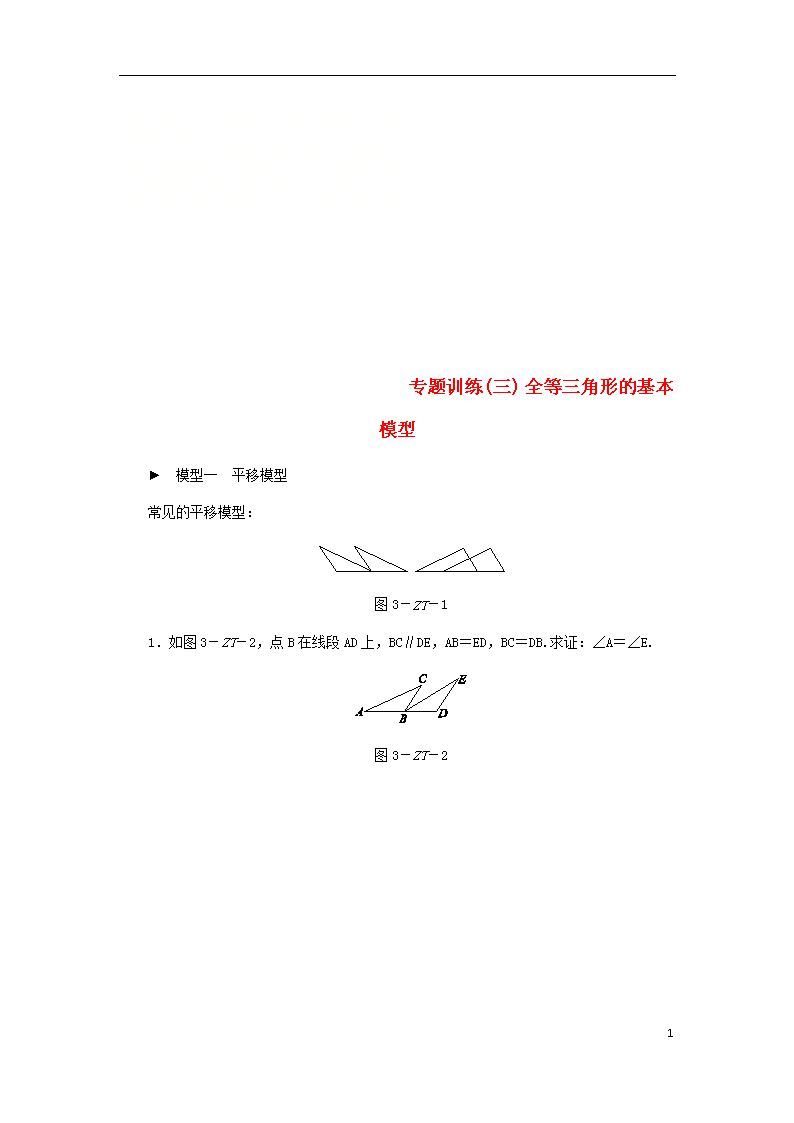

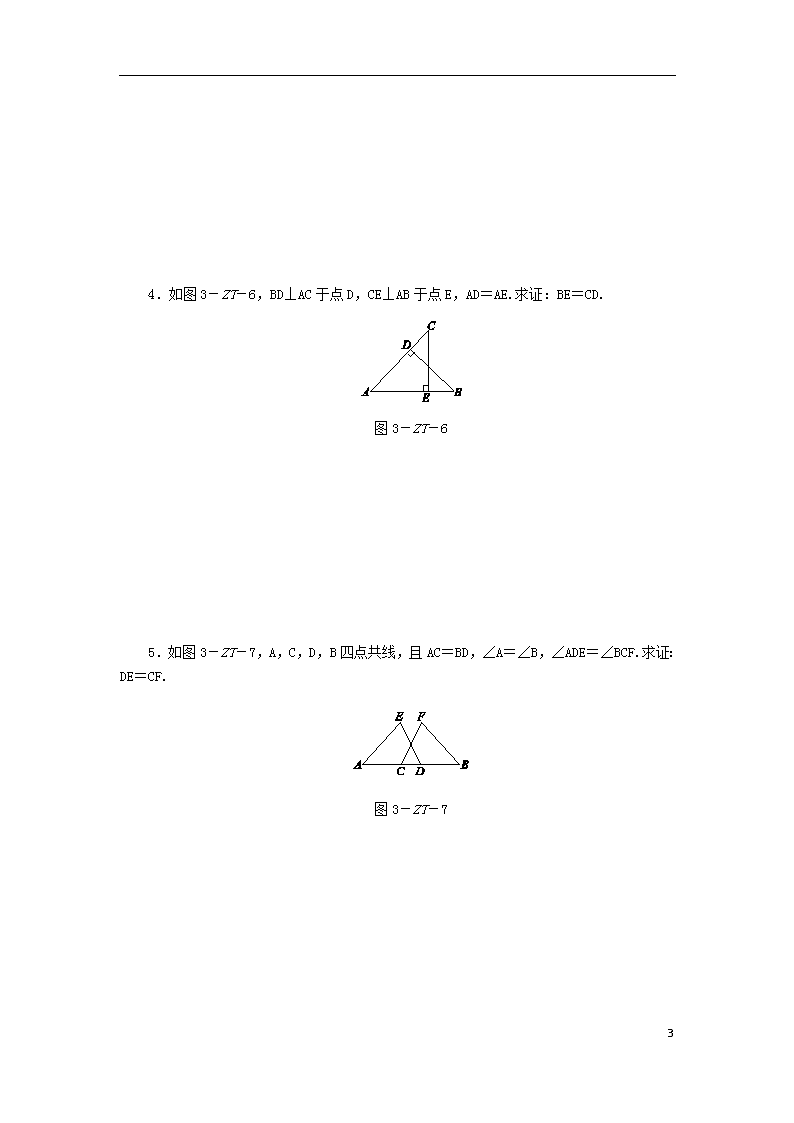
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020八年级数学上册第13章全等三角形专题训练(三)全等三角形的基本模型练习
专题训练(三) 全等三角形的基本模型 ► 模型一 平移模型 常见的平移模型: 图3-ZT-1 1.如图3-ZT-2,点B在线段AD上,BC∥DE,AB=ED,BC=DB.求证:∠A=∠E. 图3-ZT-2 12 专题训练(三) 全等三角形的基本模型 ► 模型一 平移模型 常见的平移模型: 图3-ZT-1 1.如图3-ZT-2,点B在线段AD上,BC∥DE,AB=ED,BC=DB.求证:∠A=∠E. 图3-ZT-2 12 2.如图3-ZT-3,点A,B,C,D在同一条直线上,AB=CD,AE∥BF,CE∥DF.求证:AE=BF. 图3-ZT-3 ► 模型二 轴对称模型 常见的轴对称模型: 图3-ZT-4 3.如图3-ZT-5,∠B=∠D,请添加一个条件(不得添加辅助线),使得△ABC≌△ADC,并说明理由. 图3-ZT-5 12 4.如图3-ZT-6,BD⊥AC于点D,CE⊥AB于点E,AD=AE.求证:BE=CD. 图3-ZT-6 5.如图3-ZT-7,A,C,D,B四点共线,且AC=BD,∠A=∠B,∠ADE=∠BCF.求证:DE=CF. 图3-ZT-7 12 6.如图3-ZT-8,BE⊥AC,CD⊥AB,垂足分别为E,D,BE=CD.求证:AB=AC. 图3-ZT-8 ► 模型三 旋转模型 常见的旋转模型: 图3-ZT-9 7.如图3-ZT-10,已知AB=AC,AB⊥AC,AD⊥AE,且∠ABD=∠ACE.求证:AD=AE. 12 图3-ZT-10 ► 模型四 一线三等角模型 图3-ZT-11 8.如图3-ZT-12,B,C,E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B. (1)求证:BC=DE; (2)若∠A=40°,求∠BCD的度数. 12 图3-ZT-12 ► 模型五 综合模型 平移+对称模型: 平移+旋转模型: 图3-ZT-13 图3-ZT-14 9.如图3-ZT-15,点B,F,C,E在同一条直线上,FB=CE,AB∥ED,AC∥FD,求证:AC=DF. 图3-ZT-15 12 10.如图3-ZT-16,AB=BC,BD=CE,AB⊥BC,CE⊥BC.求证:AD⊥BE. 图3-ZT-16 12 详解详析 1.证明:∵BC∥DE, ∴∠ABC=∠D. 在△ABC和△EDB中, ∵AB=DE,∠ABC=∠D,BC=DB, ∴△ABC≌△EDB(S.A.S.), ∴∠A=∠E. 2.证明:∵AE∥BF,∴∠A=∠FBD. ∵CE∥DF,∴∠D=∠ACE. ∵AB=CD,∴AB+BC=CD+BC, 即AC=BD. 在△ACE和△BDF中, ∵∠A=∠FBD,AC=BD,∠D=∠ACE, ∴△ACE≌△ABDF(A.S.A.), ∴AE=BF. 3.解:答案不唯一,如添加∠BAC=∠DAC. 理由:在△ABC和△ADC, ∵∠B=∠D,∠BAC=∠DAC,AC=AC, ∴△ABC≌△ADC(A.A.S.). 4.证明:∵BD⊥AC,CE⊥AB, ∴∠ADB=∠AEC=90°. 在△ADB和△AEC中, ∵∠ADB=∠AEC,AD=AE,∠A=∠A, 12 ∴△ADB≌△AEC(A.S.A.), ∴AB=AC. 又AD=AE, ∴AB-AE=AC-AD, 即BE=CD. 5.证明:∵AC=BD, ∴AC+CD=BD+CD, 即AD=BC. 在△AED和△BFC中, ∵∠A=∠B, AD=BC, ∠ADE=∠BCF, ∴△AED≌△BFC(A.S.A.), ∴DE=CF. 6.证明:∵BE⊥AC,CD⊥AB, ∴∠BEA=∠CDA=90°. 又∵∠A=∠A,BE=CD, ∴△ABE≌△ACD, ∴AB=AC. 7.证明:∵AB⊥AC,AD⊥AE, ∴∠BAC=∠DAE=90°. ∴∠BAC-∠DAC=∠DAE-∠DAC, 即∠BAD=∠CAE. 在△ABD和△ACE中, ∵∠BAD=∠CAE,AB=AC,∠ABD=∠ACE, 12 ∴△ABD≌△ACE,∴AD=AE. 8.解:(1)证明:∵AC∥DE, ∴∠ACB=∠E,∠ACD=∠D. ∵∠ACD=∠B, ∴∠D=∠B. 在△ABC和△CDE中, ∵∠ACB=∠E,∠B=∠D,AC=CE, ∴△ABC≌△CDE(A.A.S.), ∴BC=DE. (2)∵△ABC≌△CDE, ∴∠A=∠DCE=40°, ∴∠BCD=180°-40°=140°. 9.证明:∵FB=CE, ∴FB+FC=CE+FC,∴BC=EF. ∵AB∥ED,AC∥FD, ∴∠B=∠E,∠ACB=∠DFE. 在△ABC和△DEF中, ∵∠B=∠E,BC=EF,∠ACB=∠DFE, ∴△ABC≌△DEF(A.S.A.), ∴AC=DF. 10.证明:设 AD,BE交于点F. ∵AB⊥BC,CE⊥BC,∴∠ABD=∠C=90°. 在△ABD和△BCE中, ∵AB=BC,∠ABD=∠C,BD=CE, ∴△ABD≌△BCE, 12 ∴∠A=∠CBE. ∵∠CBE+∠ABE=90°, ∴∠A+∠ABE=90°, 则∠AFB=90°, ∴AD⊥BE. 12查看更多