勾股定理的应用复习学案

勾股定理的应用复习学案

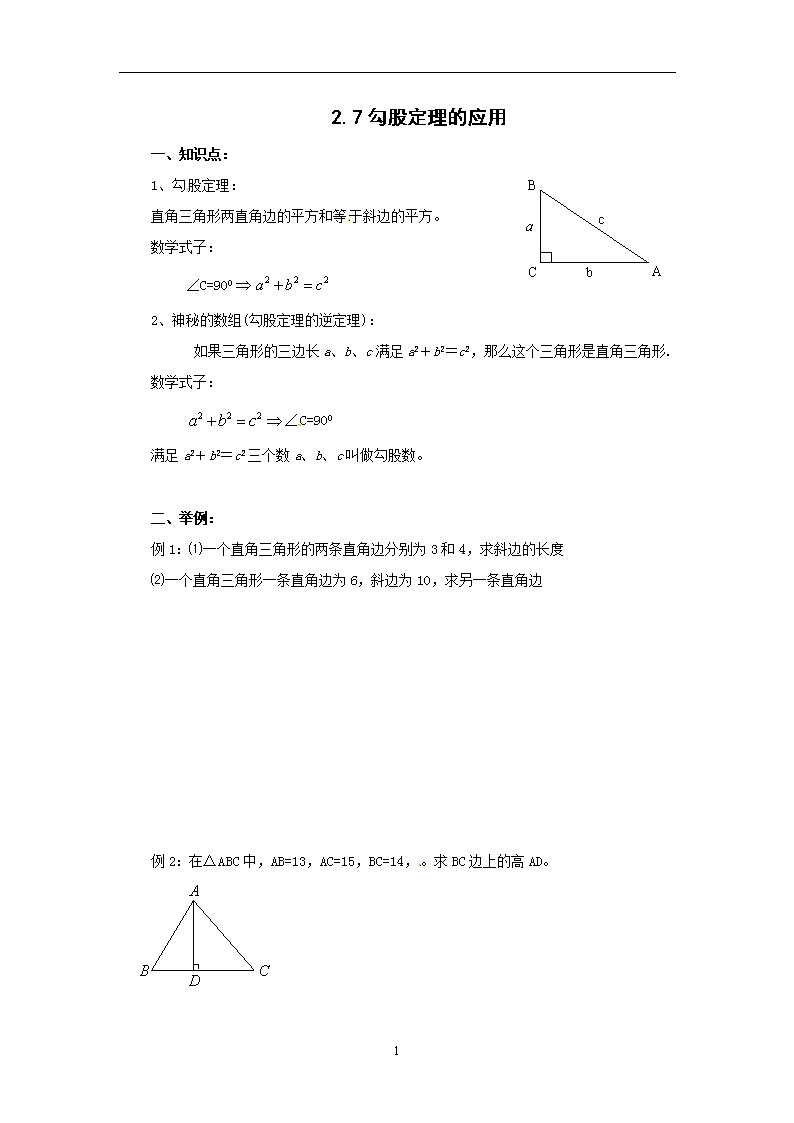
‎ ‎ ‎2.7勾股定理的应用 一、知识点：‎ C B A c b a ‎1、勾股定理：‎ 直角三角形两直角边的平方和等于斜边的平方。‎ 数学式子：‎ ‎ ∠C=900‎ ‎2、神秘的数组(勾股定理的逆定理)：‎ 如果三角形的三边长a、b、c满足a2＋b2＝c2，那么这个三角形是直角三角形.‎ 数学式子：‎ ‎ ∠C=900‎ 满足a2＋b2＝c2三个数a、b、c叫做勾股数。‎ 二、举例：‎ 例1：⑴一个直角三角形的两条直角边分别为3和4，求斜边的长度 ‎⑵一个直角三角形一条直角边为6，斜边为10，求另一条直角边 例2：在△ABC中，AB=13，AC=15，BC=14，。求BC边上的高AD。 ‎ 5‎ ‎ ‎ 例3：在△ABC中，AB=15，AC=20，BC边上的高AD=12，试求BC的长．(两解)‎ 例4：如图，在△ABC中，AC=AB，D是BC上的一点，AD⊥AB，AD=9cm，BD=15cm，求AC的长．‎ 例5：一轮船在大海中航行，它先向正北方向航行8 km，接着，它又掉头向正东方向航行15千米．⑴ 此时轮船离开出发点多少km? ⑵ 若轮船每航行1km，需耗油0.4升，那么在此过程中轮船共耗油多少升?‎ 例6：如图，有一块直角三角形纸片，两直角边AC＝6cm， BC＝8cm，现将直角边AC沿直线折叠，使它落在斜边AB上，且点C落到E点，则CD的长是多少?‎ 5‎ ‎ ‎ 例7：如图，四边形ABCD中，AB=3，BC=4，CD=12，AD=13，∠B=90°，求四边形ABCD的面积。‎ ‎ ‎ B ‎ ‎ A ‎ ‎ C ‎ ‎ D ‎ ‎ 例8：有一根70cm的木棒，要放在50cm，40cm，30cm的木箱中，试问能放进去吗？‎ 例9：甲、乙两人在沙漠进行探险，某日早晨8∶00甲先出发，他以6千米/时速度向东南方向行走，1小时后乙出发，他以5千米/时速度向西南方向行走，上午10∶00时，甲、乙两人相距多远？‎ 5‎ ‎ ‎ 例10：如图，由5个小正方形组成的十字形纸板，现在要把它剪开，使剪成的若干块能够拼成一个大正方形。‎ （1） 如果剪4刀，应如何剪拼？‎ （2） 少剪几刀，也能拼成一个大正方形吗？‎ 三、作业： ‎ ‎1、Rt△ABC中，∠C=900‎ ‎⑴如果BC=9，AC=12，那么AB= 。‎ ‎⑵如果BC=8，AB =10，那么AC = 。‎ ‎⑶如果AC=20，BC =25，那么AB= 。‎ ‎⑷如果AB=13，AC=12，那么BC= 。‎ ‎⑸如果AB=61，BC=11，那么AC= 。‎ ‎2、若直角三角形两直角边长分别为5和12，求其斜边上的高为。 ‎ ‎3、若直角三角形的三边分别为x，6，8，求x的值。‎ ‎4、已知：等边三角形 ABC的边长为6cm，求一边上的高和三角形的面积。‎ 5‎ ‎ ‎ ‎5、等腰三角形ABC的腰长为10，底边上的高为6，则底边的长为多少？ ‎ 5‎