河南省洛阳市洛宁县2019-2020学年第二学期期末考试八年级数学试卷

河南省洛阳市洛宁县2019-2020学年第二学期期末考试八年级数学试卷

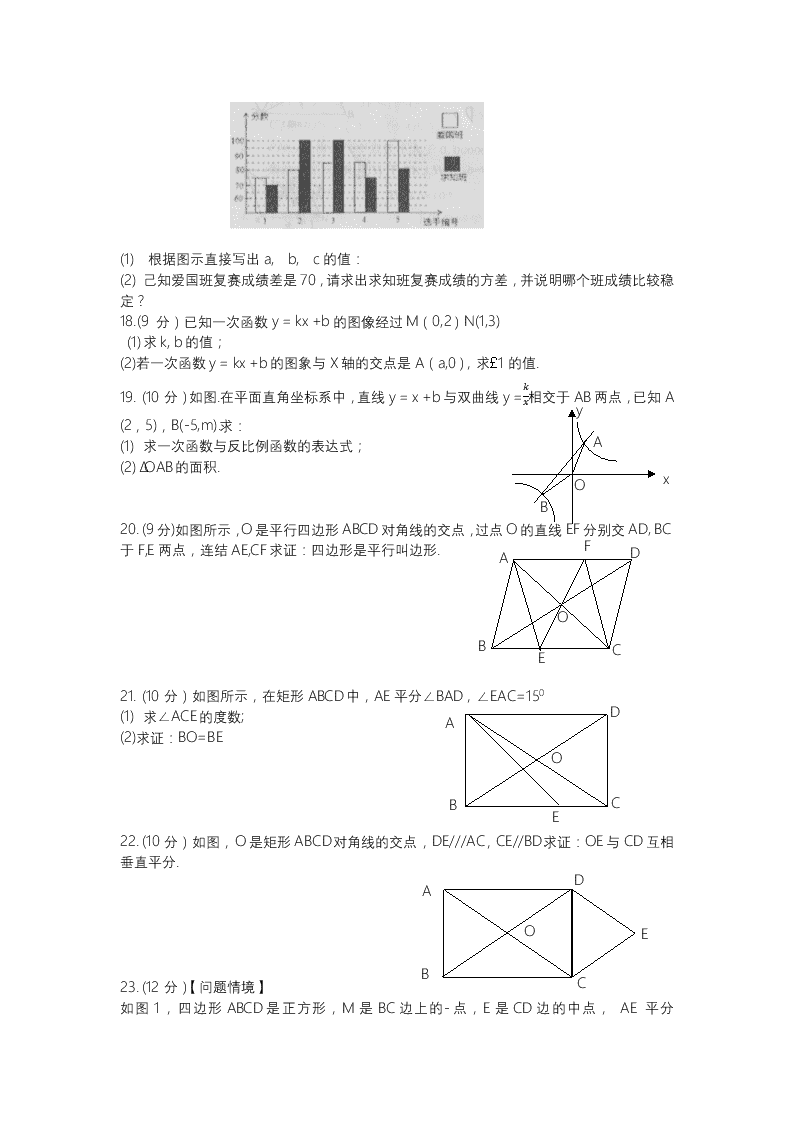
河南省洛阳市洛宁县2019-2020学年第二学期期末考试八年级 数学试卷 一、选择题（本大题共10小题，共30分）‎ ‎1. 使分式‎2‎x-3‎有意义的x的取值范围是（ ）‎ A. x>3 B.‎ x≠‎3 C. x<3 D.‎ x=3‎ ‎2. 将‎1‎‎5‎‎-1‎‎,‎-3‎‎0‎,‎‎(-4)‎‎2‎这三个数按从小到大的顺序排列，结果正确的是( )‎ A. ‎1‎‎5‎‎-1‎‎<‎-3‎‎0‎<‎‎(-4)‎‎2‎ B.‎‎(-4)‎‎2‎‎<‎‎1‎‎5‎‎-1‎‎<‎‎-3‎‎0‎ C.‎ ‎-3‎‎0‎<‎1‎‎5‎‎-1‎<‎‎-4‎‎2‎ D. ‎‎-3‎‎0‎‎<‎‎-4‎‎2‎‎<‎‎1‎‎5‎‎-1‎ ‎3. PM‎2.5‎是指大气中直径不大于0. 0000025米的颗粒物，将0. 0000025用科学记数法表示为（ ）‎ A. 2.5x10-7 B. 2.5x10-6 C. 25 x 10-7 D. 0.25x10-5‎ ‎4. 下表记录了甲、乙、丙、丁四名同学参加某区“中华魂”主题教育演讲比赛的相关数据：根据表中数据，要从中选择一名成绩好且发挥稳定的同学参加市级比赛，应该选择（ ）‎ 甲 乙 丙 丁 平均数（分）‎ ‎90‎ ‎80‎ ‎90‎ ‎80‎ 方差 ‎2.4‎ ‎2.2‎ ‎5.4‎ ‎2.4‎ A.甲 B.乙 C.丙 D. 丁 ‎5. 已知正比例函数y = kx(k‎≠‎0)的函数值y随的增大而减小，‎ y = x +k 的图象大致是图中的( )‎ ‎6. 如图，点A在反比例函数y = kx (x>0, k>0)的图象上，AB丄x轴于点B,点C在X轴的负半轴上，且BO = 2CO,若ΔABC面积为18,则k的值为（ ）‎ A. 12 B. 18 C. 20 D.24‎ ‎7. 下列判断错误的是（ ）‎ A.两组对边分别相等的四边形是平行四边形 B.四个内角都相等的四边形是矩形 C.两条对角线垂直且平分的四边形是正方形 D.四条边都相等的四边形是菱形 ‎8. 如图所示，‎▫‎ABCD中，AC的垂直平分线交于点E，且ΔCDE的周长为8,则‎▫‎ABCD的周长是（ ）‎ A. 10 B. 12 C. 14 D. 16‎ ‎9. 如图，四边形是菱形， AC=8, DB=6, DH丄AB于H,‎ A B C D H DH等于（ ）‎ A. ‎24‎‎5‎ B. ‎12‎‎5‎ C. 5 D. 4‎ A B C D E F ‎10. 如图，在‎▫‎ABCD中，用直尺和圆规作∠BAD的平分线AG交BC点E，若BF=12,AB=10，则AE的长为（ ）‎ A. 15 B. 16 C. 14 D. 13‎ 二、填空题（本大题共5小题，共15分）‎ ‎11. 计算：m‎2m+1‎+m+1‎‎2m+1‎=‎ ‎12. 在‎▫‎ABCD中，∠B +∠D = 2000，则∠A=‎ ‎13. 已知正比例函数;y = (3m-2)x的图像上两点A（x1, y1),B(x2 , y2)，当x1 < x2时 ,有y1 >y2那么m的取值范围是 . ‎ ‎14. 如果一组数据-3, -2，0，1, x, 6，9，12的平均数为3,那么这组数据的中位数是 .‎ ‎15. 如图所示，正方形ABCD的边长为4, E是边BC上的一点，且BE=1，p是对角线AC上的一动点，连接PB、PE，当点P在AC上运动时，△PBE周长的最小值是 ‎ A B C D P E 三、解答题（本大题共8小题，共75分） &‎ ‎16. (7分）先化简，再求值：a‎2‎‎-2ab+‎b‎2‎‎2a-2b‎÷(‎‎1‎b-‎1‎a),其中a=2,b= 3 ^‎ ‎17. (8分）某校初一开展英语拼写大赛，爱国班和求知班根据初赛成绩，各选出5 名选手参加复赛，两个班备选出的5名选手的复赛成绩如图所示：‎ 班级 平均数（分）‎ 中位数（分）‎ 众数（分）‎ 爱国班 a ‎85‎ c 求知班 ‎85‎ b ‎100‎ ‎(1) 根据图示直接写出a, b, c的值：‎ ‎(2) 己知爱国班复赛成绩差是70，请求出求知班复赛成绩的方差，并说明哪个班成绩比较稳定？ ‎ ‎18.(9 分）已知一次函数y = kx +b的图像经过M（0,2）N(1,3)‎ ‎ (1)求k, b的值；‎ ‎(2)若一次函数y = kx +b的图象与X轴的交点是A（a,0），求£1的值.‎ B O x y A ‎19. (10分）如图.在平面直角坐标系中，直线y = x +b与双曲线y =kx相交于AB两点，已知A (2，5)，B(-5,m).求：‎ ‎(1) 求一次函数与反比例函数的表达式；‎ ‎(2)ΔOAB的面积.‎ A B C D O E F ‎20. (9分)如图所示，O是平行四边形ABCD对角线的交点，过点O的直线EF分别交AD, BC于F,E两点，连结AE,CF求证：四边形是平行叫边形.‎ D ‎21. (10分）如图所示，在矩形ABCD中，AE平分∠BAD，∠EAC=150‎ A ‎(1) 求∠ACE的度数;‎ O ‎(2)求证：BO=BE C B E A B D C E O ‎22. (10分）如图，O是矩形ABCD对角线的交点，DE///AC，CE//BD.求证：OE与CD互相垂直平分.‎ ‎23. (12分）【问题情境】‎ 如图1，四边形ABCD是正方形，M是BC边上的-点，E是CD边的中点， AE 平分 ‎∠DAM.‎ ‎【探究展示】‎ D ‎ (1)证明：AM= AD+MC;‎ ‎(2)AM=AD+MC是否成立？若成立，请给出证明；若不成立，请说明理由. ‎ ‎【拓展延伸】‎ C ‎ (3)若四边形ABCD是长与宽不相等的矩形，其他条件不变，如图2,探究 展示（1)、（2)中的结论是否成立？请分别作山判断，不需要证明.‎ A B C D E M A C B D E M 八年级参考答案 ‎1.B 2.C 3.B 4.A 5.B 6.D 7.C 8.D 9.A 10.B ‎11.1 12.​80 13.​ 14.1 15.6 16.原式................................................................2分 ‎............................................................................................4分 ‎，..........................................5分 当a=2，b=3时，‎ 原式．..................................7分 ‎ ‎ ‎ ‎ ‎ ‎ ‎17.解：（1）a=85 ；b =80； c=85； ..................................6分（各2分） （2）爱国班比求知班成绩更平稳一些．理由如下： S2爱国班=70， S2求知班=[（70-85）2+（100-85）2+（100-85）2+（75-85）2+（80-85）2]=160，..7分 ∵S2爱国班＜S2求知班， ∴爱国班比求知班成绩更平稳一些．.......................8分 ‎ ‎18.解：（1）由题意得：，.......................4分 解得：；...........................................6分 （2）把A（a，0）代入y=x+2得，a+2=0，..................8分 解得a=-2；..............................................9分 19. 解：（1）把点A（2，5）代入反比例函数得：，........1分 解得：k=10，...................................................2分 即反比例函数的解析式为：y=，..................................3分 把点A（2，5）代入y=x+b得：2+b=5，............................4分 解得b=3，........................................................5分 即一次函数的表达式为：y=x+3，....................................6分 （2）把点B(-5,m)代入y=x+3得，m=-2...............................7分 ∴点B（-5，-2），...........................8分 把y=0代入一次函数y=x+3得： x+3=0， 解得：x=-3， 即点C的坐标为：（-3，0），OC的长为3， 点A到OC的距离为5，点B到OC的距离为2， S△AOB=S△OAC+S△OBC = =，............................................10分 20.证明：∵四边形ABCD是平行四边形， ∴OD=OB，OA=OC，....................................2分 ∵AB∥CD， ∴∠DFO=∠BEO，∠FDO=∠EBO，..................................4分 ∴在△FDO和△EBO中， ∴△FDO≌△EBO（AAS），..................................6分 ∴OF=OE，.................................................7分 ∵OA=OC，.................................................8分 ​∴四边形AECF是平行四边形．...............................9分 21.（1）解：∵在矩形ABCD中，AE平分∠BAD，∠EAC=15°， ∴∠AEB=∠EAD=45°，....................................3分 ∴∠ACE=∠AEB-∠EAC=45°-15°=30°；........................5分 （2）证明：由（1）可知∠ACE=30°， ∴∠BAO=60°，.......................................................6分 ‎ ‎∵OA=OB ∴是等边三角形................................................7分 ∴OB=AB，............................................................8分 ∵∠AEB=∠EAD=∠BAE=45°， ∴AB=BE，..........................................................9分 ∴BO=BE........................................................................................................................10分 22.证明：∵四边形ABCD是矩形， ∴AC=BD，OA=OC=OD=OB（矩形的对角线相等且互相平分），...........2分 又∵DE∥AC，CE∥BD， ∴四边形OCED是平行四边形，................................5分 又∵OC=OD， ∴四边形OCED是菱形，........................................8分 ∴OE⊥CD且OE与CD互相平分（菱形的对角线互相垂直平分）．.....10分 ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎23.【答案】方法一： （1）解：（6分）如图1（1）过点E作EF⊥AM交AM于F点，连接EM，........1分 ∵AE平分∠DAM ∴∠DAE=∠EAF.........................................2分 在△ADE和△AFE中， AE=AE ∠D=∠AFE=90° ∴△ADE≌△AEF（ASA）..................................3分 ∴AD=AF，EF=DE=EC，..................................4分 在中， ∴△EFM≌△ECM（HL）..................................5分 ∴FM=MC，AM=AF+FM=AD+MC....................................................6分 方法二： 证明：延长AE、BC交于点N，如图1（2），................1分 ∵四边形ABCD是正方形， ∴AD∥BC． ∴∠DAE=∠ENC ∵AE平分∠DAM， ∴∠DAE=∠MAE． ∴∠ENC=∠MAE． ∴MA=MN．....................................................2分 ‎ 在△ADE和△NCE中， ∴△ADE≌△NCE（AAS）．...................................4分 ∴AD=NC．..................................................5分 ∴MA=MN=NC+MC =AD+MC．...................................6分 （2）（4分）AM=DE+BM成立．.........................7分 方法一： 证明：将△ADE绕点A顺时针旋转90°，得到新△ABF，如图1（3） ∴BF=DE，∠F=∠AED．........................8分 ∵AB∥DC， ∴∠AED=∠BAE． ∵∠FAB=∠EAD=∠EAM， ∴∠AED=∠BAE=∠BAM+∠EAM=∠BAM+∠FAB=∠FAM． ∴∠F=∠FAM． ∴AM=FM．.............................................9分 ∴AM=FB+BM=DE+BM.......................................................................10分 方法二： 证明：过点A作AF⊥AE，交CB的延长线于点F，如图1（4）所示． ∵四边形ABCD是正方形， ∴∠BAD=∠D=∠ABC=90°，AB=AD，AB∥DC． ∵AF⊥AE， ∴∠FAE=90°． ∴∠FAB=90°-∠BAE=∠DAE． 在△ABF和△ADE中， ∴△ABF≌△ADE（ASA）．.....................................8分 ∴BF=DE，∠F=∠AED． ∵AB∥DC， ∴∠AED=∠BAE． ∵∠FAB=∠EAD=∠EAM， ∴∠AED=∠BAE=∠BAM+∠EAM =∠BAM+∠FAB =∠FAM． ∴∠F=∠FAM． ∴AM=FM．..................................................9分 ∴AM=FB+BM=DE+BM．.........................................10分 ‎ ‎（3）（2分）①结论AM=AD+MC仍然成立．②结论AM=DE+BM不成立．..............12分