小结与思考（2）

小结与思考（2）

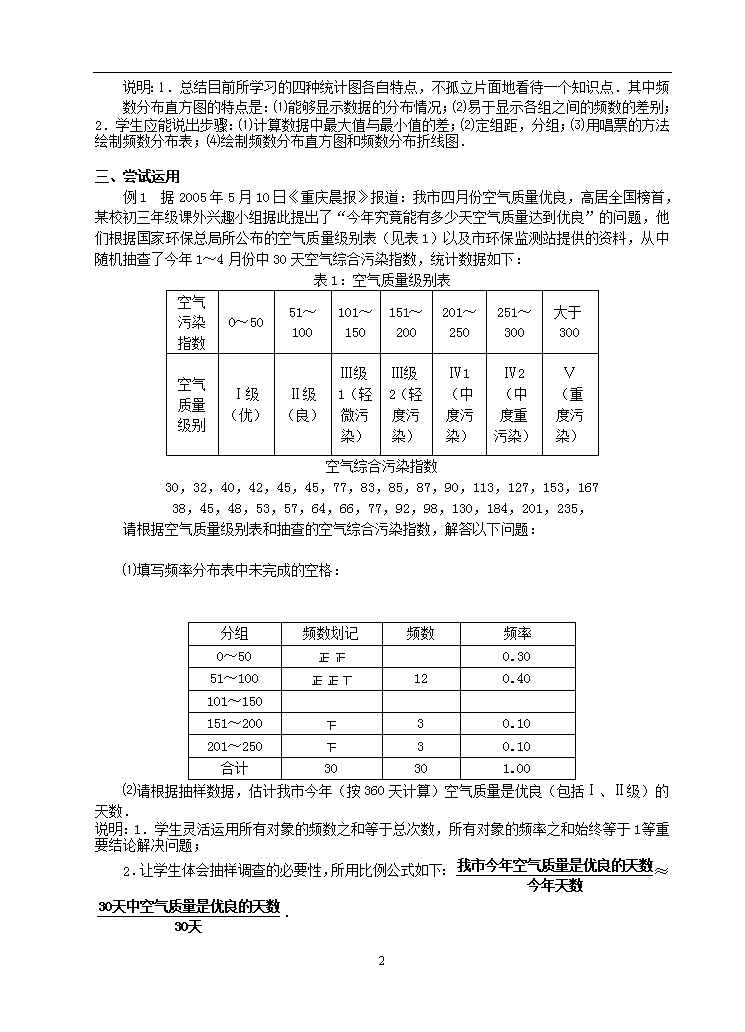
学科 数学 年级 八 课题 小结与思考（2）‎ 主备人 潘明璋 教 学 目 标 ‎1.从事收集、整理、描述和分析数据的活动，并能用计算器处理较为复杂的统计数据。‎ ‎2.会用三种统计图表示数据。‎ 教 学 重难点 教学重点 会用三种统计图表示数据 教学难点 会用三种统计图表示数据 教学过程 一、情境创设 情景1 学生回忆本章所学习的内容，画出知识框图．‎ ‎ 说明：通过回忆和画知识框图，会进一步强化学生对本章知识的整体把握．‎ 二、新知探究 情景2 为配和新课程的实施，某市举行了“应用与创新”知识竞赛，共有1万名学生参加了这次竞赛（满分100分，得分全为整数）．为了解本次竞赛成绩情况，从中随机抽取了部分学生的竞赛成绩，进行统计，整理见下表：‎ 组别 分 组 频 数 频率 ‎1‎ ‎49.5～59.5‎ ‎60‎ ‎0.12‎ ‎2‎ ‎59.5～69.5‎ ‎120‎ ‎0.24‎ ‎3‎ ‎69.5～79.5‎ ‎180‎ ‎0.36‎ ‎4‎ ‎79.5～89.5‎ ‎130‎ ‎5‎ ‎89.5～99.5‎ ‎0.02‎ 合 计 ‎1.00‎ 解答下列问题：‎ ‎⑴在这个问题中，样本容量a ＝ ；‎ ‎⑵第五小组的频数b ＝ ，第四小组的频率c ＝ ．‎ 说明：1．此情景通过实际问题，让学生感受抽样调查的必要性，复习了频数、频率、频数分布表等概念；‎ ‎2．该题要求学生灵活运用所有对象的频数之和等于总次数，所有对象的频率之和始终等于1 等重要结论解决问题；‎ ‎3．频数和频率都能够反映每个对象出现的频繁程度．‎ 答案：500，10，0.26．‎ 问题1 扇形统计图、条形统计图、折线统计图和频数分布直方图各有什么特点？‎ 问题2 用频数分布直方图、频数分布折线图对数据进行表示和处理的步骤是什么？‎ 5‎ 说明：1．总结目前所学习的四种统计图各自特点，不孤立片面地看待一个知识点．其中频 数分布直方图的特点是：⑴能够显示数据的分布情况；⑵易于显示各组之间的频数的差别；‎ ‎2．学生应能说出步骤：⑴计算数据中最大值与最小值的差；⑵定组距，分组；⑶用唱票的方法绘制频数分布表；⑷绘制频数分布直方图和频数分布折线图．‎ 三、尝试运用 例1 据2005年5月10日《重庆晨报》报道：我市四月份空气质量优良，高居全国榜首，某校初三年级课外兴趣小组据此提出了“今年究竟能有多少天空气质量达到优良”的问题，他们根据国家环保总局所公布的空气质量级别表（见表1）以及市环保监测站提供的资料，从中随机抽查了今年1～4月份中30天空气综合污染指数，统计数据如下：‎ 表1：空气质量级别表 空气污染指数 ‎0～50‎ ‎51～100‎ ‎101～150‎ ‎151～200‎ ‎201～250‎ ‎251～300‎ 大于300‎ 空气质量级别 Ⅰ级（优）‎ Ⅱ级（良）‎ Ⅲ级1（轻微污染）‎ Ⅲ级2（轻度污染）‎ Ⅳ1（中度污染）‎ Ⅳ2（中度重污染）‎ Ⅴ（重度污染）‎ 空气综合污染指数 ‎30，32，40，42，45，45，77，83，85，87，90，113，127，153，167‎ ‎38，45，48，53，57，64，66，77，92，98，130，184，201，235，‎ 请根据空气质量级别表和抽查的空气综合污染指数，解答以下问题：‎ ‎⑴填写频率分布表中未完成的空格：‎ 分组 频数划记 频数 频率 ‎0～50‎ ‎0.30‎ ‎51～100‎ ‎12‎ ‎0.40‎ ‎101～150‎ ‎151～200‎ ‎3‎ ‎0.10‎ ‎201～250‎ ‎3‎ ‎0.10‎ 合计 ‎30‎ ‎30‎ ‎1.00‎ ‎⑵请根据抽样数据，估计我市今年（按360天计算）空气质量是优良（包括Ⅰ、Ⅱ级）的天数．‎ 说明：1．学生灵活运用所有对象的频数之和等于总次数，所有对象的频率之和始终等于1 等重要结论解决问题；‎ ‎2．让学生体会抽样调查的必要性，所用比例公式如下：≈．‎ 5‎ 解：⑴ 9，，3，0.10；‎ ‎⑵因为（天），所以估计我市今年空气质量是优良的天数有252天．‎ 例2 为了参加学校年级之间的广播体操比赛，七年级准备从63名同学中挑出身高相差不多的40名同学参加比赛．为此收集到这63名同学的身高（单位：cm）数据如下：‎ ‎158‎ ‎158‎ ‎160‎ ‎168‎ ‎159‎ ‎159‎ ‎151‎ ‎158‎ ‎159‎ ‎168‎ ‎158‎ ‎154‎ ‎158‎ ‎154‎ ‎169‎ ‎158‎ ‎158‎ ‎158‎ ‎159‎ ‎167‎ ‎170‎ ‎153‎ ‎160‎ ‎160‎ ‎159‎ ‎159‎ ‎160‎ ‎149‎ ‎163‎ ‎163‎ ‎162‎ ‎172‎ ‎161‎ ‎153‎ ‎156‎ ‎162‎ ‎162‎ ‎163‎ ‎157‎ ‎162‎ ‎162‎ ‎161‎ ‎157‎ ‎157‎ ‎164‎ ‎155‎ ‎156‎ ‎165‎ ‎166‎ ‎156‎ ‎154‎ ‎166‎ ‎164‎ ‎165‎ ‎156‎ ‎157‎ ‎153‎ ‎165‎ ‎159‎ ‎157‎ ‎155‎ ‎164‎ ‎156‎ 选择身高在哪个范围的学生参加呢？‎ 说明：此例题应把握以下几点：‎ ‎１．让学生体会将数据分组的必要性，做到合理分组，即当数据在100个以内时，根据数据的多少通常分成5～12个组；‎ ‎２．注意识图的重要性，从图表中获取重要的信息；‎ ‎３．根据数据处理的结果，做出合理的判断和预测，体会统计对决策的作用．‎ 解：为了使参赛选手的身高比较整齐，需要了解数据（身高）的分布情况．将数据适当分组整理可得下面的频数分布表：‎ 身高分组 频数划记 频 数 ‎148.5～151.5‎ ‎2‎ ‎151.5～154.5‎ 正 ‎6‎ ‎154.5～157.5‎ 正正 ‎12‎ ‎157.5～160.5‎ 正正正 ‎19‎ ‎160.5～163.5‎ 正正 ‎10‎ ‎163.5～166.5‎ 正 ‎8‎ ‎166.5～169.5‎ ‎4‎ ‎169.5～172.5‎ ‎2‎ 为了更清楚地看出频数分布的情况，可以根据上表画出频数分布直方图、频数分布折线图：‎ 5‎ 从图中可以看出，身高在154.5～157.5，157.5～160.5，160.5～163.5三个组的人数最多，一共有12＋19＋10＝41人，因此可以从身高在154.5～163.5之间的学生中选队员．‎ 四、解决问题 ‎1、为调查居民生活环境情况，环保局对所辖的52个居民区进行了噪音（单位：分贝）水平的调查，结果如下图．‎ 请根据直方图回答下列问题：‎ ‎⑴在噪音最高的居民区，噪音水平在那个范围内？‎ ‎ ⑵噪音水平低于65分贝的有多少个居民区？‎ ‎⑶最高的长方形的高代表了哪个范围的噪音水平？‎ ‎⑷了解有关噪音方面的知识，并尝试评价这个地区的噪音污染情况，提出几条降低噪音的建议．‎ ‎2、七年级1班40个学生某次数学测验成绩如下：‎ ‎63，84，91，53，69，81，61，69，91，78，75，81，80，67，76，81，79，94，61，69，89，70，70，87，81，86，90，88，85，67，71，82，87，75，87，95，53，65，74，77‎ 数学老师按10分的组距分段，算出每个分数段学生成绩出现的频数，填入频数分布表：‎ ‎⑴请把频数分布表及频数分布直方图补充完整；‎ ‎⑵请说明哪个分数段的学生最多？哪个分数段的学生最少？‎ ‎⑶请你帮老师统计一下这次数学考试的及格率（60分以上含60分为及格）及优秀率（90分以上含90分为优秀）.‎ 说明：练习1是让学生从直方图中获取信息，做出判断及合理推测；练习2是中考题，体现了中考的考察方向．‎ 五、 课堂小结 本章内容有什么收获?‎ 5‎ 作业设计：‎ 同步练习 小结与思考 5‎