湖南省邵阳市隆回县2019-2020学年八年级下学期期末考试数学试题

湖南省邵阳市隆回县2019-2020学年八年级下学期期末考试数学试题

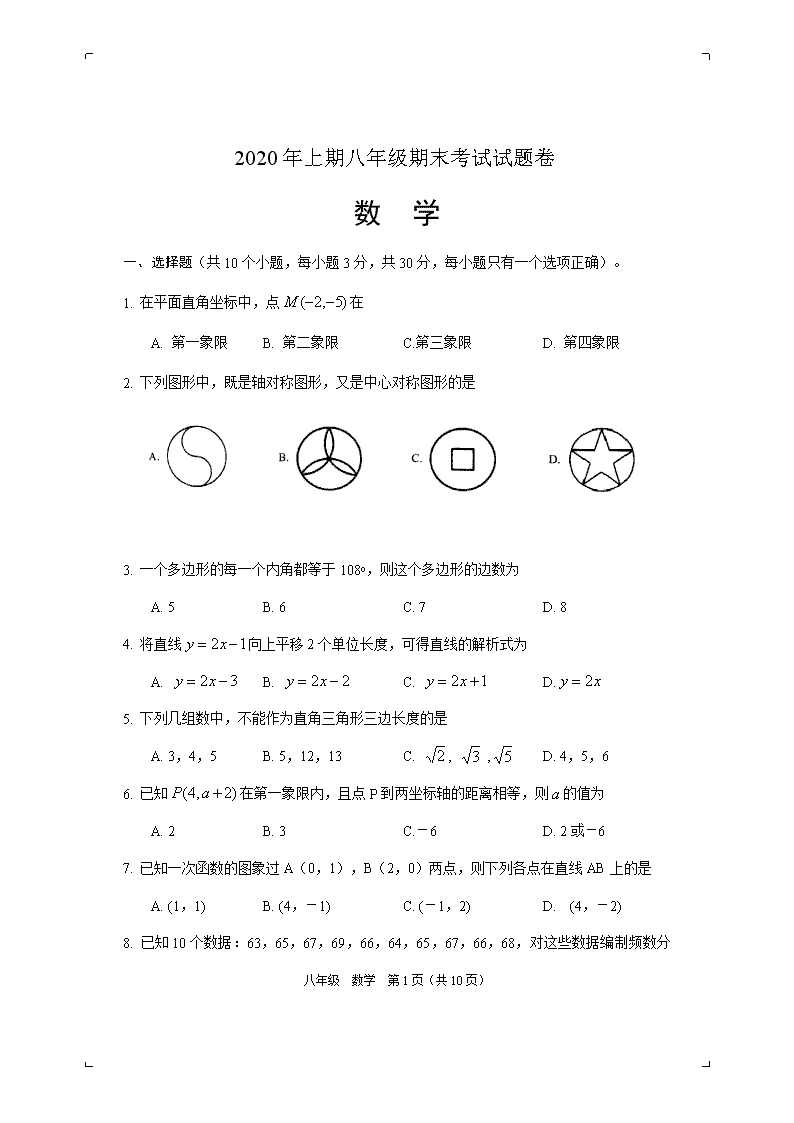
‎2020年上期八年级期末考试试题卷 数 学 一、选择题（共10个小题，每小题3分，共30分，每小题只有一个选项正确）。‎ ‎1. 在平面直角坐标中，点在 A. 第一象限 B. 第二象限 C.第三象限 D. 第四象限 ‎2. 下列图形中，既是轴对称图形，又是中心对称图形的是 ‎ ‎ ‎ ‎ ‎3. 一个多边形的每一个内角都等于108o，则这个多边形的边数为 A. 5 B. 6 C. 7 D. 8‎ ‎4. 将直线向上平移2个单位长度，可得直线的解析式为 A. B. C. D.‎ ‎5. 下列几组数中，不能作为直角三角形三边长度的是 A. 3，4，5 B. 5，12，13 C. , , D. 4，5，6‎ ‎6. 已知在第一象限内，且点P到两坐标轴的距离相等，则的值为 A. 2 B. 3 C.－6 D. 2或－6‎ ‎7. 已知一次函数的图象过A（0，1），B（2，0）两点，则下列各点在直线AB上的是 A. (1，1) B. (4，－1) C. (－1，2) D. (4，－2)‎ 八年级 数学 第10页（共10页）‎ ‎8. 已知10个数据：63，65，67，69，66，64，65，67，66，68，对这些数据编制频数分布表，那么数据在64.5~67.5之间的频率为： ‎ A. 0.5 B. 0.6 C. 5 D. 6‎ ‎9. 已知矩形的对角线长为10，两邻边之比为3:4，则矩形的面积为 A. 50 B. 48 C. 24 D. 12‎ ‎10. 已知四边形ABCD是平行四边形，从以下四个条件：①AB=BC，②∠ABC=900，③AC=BD，④AC⊥BD中选出两个条件，能得到□ABCD是正方形，下列四种选法中错误的是 A. 选①② B. 选①③ C. 选②④ D. 选②③‎ 二、填空题（共8个小题，每小题3分，共24分）‎ ‎11. 若直角三角形的斜边长为16，则这个直角三角形斜边的中线长为 。‎ ‎12. 若一次函数是正比例函数，则m= 。‎ ‎13. 已知点A（，2）与点B（4，2）关于轴对称，则= 。‎ ‎14. 如图，在△ABC中，AB=3，AC=5，点D，E，F分别为AB，BC，AC边的中点，则四边形ADEF的周长为 。‎ ‎（14题图）‎ ‎15. 菱形的周长是20，一条对角线长为8，则这个菱形的面积为 。‎ ‎（16题图）‎ ‎16. 如图，△ABC中，已知AB=5，AC=4，AD平分∠BAC交BC于D，DE⊥AC交AC于点E，若DE=2，则△ABC的面积为 。‎ ‎17. 如图，已知点P是正方形ABCD对角线BD上一点，且BP=BC，‎ 则∠DCP的度数为 。‎ ‎（17题图）‎ ‎18. 某书定价每本20元，如果一次购买超过10本，超过10本的部 八年级 数学 第10页（共10页）‎ 分每本只需15元，若未超过10本，每本仍需20元，则购书金 额（单位：元）与购买数量（单位：本）之间的函数表达式为 。‎ 三、解答题（共7个小题，19~21小题每小题6分。22~25小题每题7分，共46分）‎ ‎19. 如图，已知点M（－2，0）点N（0，6），A为线段MN上一点，AB⊥轴，垂足为B，AC⊥轴，垂足为点C。‎ ‎（1）求直线MN的函数表达式 ‎（2）若点A的横坐标为－1，求矩形ABOC的面积 20. ‎△ABC在平面直角坐标系中的位置如图所示 （1） 作出△ABC关于轴对称的△A1B1C1；并写出点A的对应点A1的坐标。‎ （2） 将△ABC向下平移5个单位长度，画出平移后的△A2B2C2，并写出点A的对应点A2的坐标。‎ ‎21. 如图，在平行四边形ABCD中，E为BC边上的一点，连结AE，BD且AE=AB。‎ ‎（1）求证：∠ABE=∠EAD ‎（2）若∠AEB=2∠ADB，求证平行四边形ABCD是菱形。‎ 八年级 数学 第10页（共10页）‎ 22. 某校举行了书法比赛，评委对所有参赛选手作品进行了打分，将成绩绘制成频数分布表和频数直方图的一部分如下：‎ 成绩 频数（人数）‎ 频率 ‎50≤＜60‎ ‎35‎ ‎0.175‎ ‎60≤＜70‎ ‎70≤＜80‎ ‎70‎ ‎0.35‎ ‎80≤＜90‎ ‎40‎ ‎0.2‎ ‎90≤＜100‎ ‎10‎ ‎0.05‎ 根据以上信息，解答下列问题：‎ （1） 参赛选手的总人数为 （人），= ，= ；‎ （2） 请补全频数分布直方图。‎ （3） 拟对参赛选手前25%进行奖励，问获奖选手的最低分数线是多少？‎ 23. 如图，把长方形ABCD沿对角线BD折叠，重合部分为△EBD。‎ （1） 求证：△EBD为等腰三角形 （2） 若AB=2，BC=8，求AE的长。‎ 八年级 数学 第10页（共10页）‎ 八年级 数学 第10页（共10页）‎ 22. 端午节期间，小明一家自驾游去了离家200km的某地，下图是他们离家的距离与汽车行驶时间的函数图象，根据图象解答下列问题：‎ （1） 求出线段AB函数表达式 （2） 求他们离家182km时，共用了多少小时？（提示：图中的OA，AB，BC均为线段）‎ 23. 将两个全等的直角三角形ABC和DBE按图①方式摆放，其中∠ACB=∠DEB=900，∠A =∠D=300，点E落在AB上，DE所在直线交AC所在直线于点F。‎ （1） 连接BF，求证：CF=EF。‎ （2） 若将图①中的△DBE绕点B按顺时针方向旋转角，且0o＜＜60o，其他条件不变，如图②，求证：AF+EF=DE。‎ （3） 若将图①中的△DBE绕点B按顺时针方向旋转角β，且60o＜β＜180o，其他条件不变，如图③，你认为（2）中的结论还成立吗？若成立，写出证明过程：若不成立，请直接写出AF、EF与DE之间的数量关系。 ‎ 八年级 数学 第10页（共10页）‎ 八年级 数学 第10页（共10页）‎ ‎2020年上期八年级期末考试 数学参考答案 一、选择题（每题3分，共30分）。‎ CCACD ABBBD 二、填空题（每题3分，共24分）‎ ‎11. 8； 12. 2； 13. -4； 14. 8； 15. 24； 16. 9； 17. 22.5o； ‎ ‎18.‎ 三、解答题。‎ ‎19.（1）设直线MN的表达式为（1分），把M,N坐标代入直线方程得 （2分） 解得 直线MN函数表达式为：（3分）‎ ‎（2）把代入，得，点A坐标为（，3）（4分）‎ AB=3，AC=1（5分），矩形ABOC的面积S=1×3=3（6分）‎ ‎20.（1）图略（2分），A1（2，3）（3分）‎ ‎（2）图略（5分），A2（-2，-2）（6分）‎ ‎21.（1）ABCD为平行四边形，（1分）‎ 又AB=AE （2分）‎ 八年级 数学 第10页（共10页）‎ ‎（3分）‎ ‎（2） ABCD是平行四边形，（4分）‎ 又由（1）知 ‎（5分）‎ ‎∴AB=AD ‎∴□ABCD为菱形（6分）‎ 22. ‎（1）总人数为：200人（1分），a=45（2分） b=0.225（3分）‎ ‎（2）略（5分）‎ ‎（3）奖励人数为200×25%＝50（人）（6分）∴获奖选手的最低分数为80分（7分）‎ ‎23. （1）∵Rt△BDC’≌Rt△BDC ∴∠EBD=∠DBC（1分）‎ 又∵ABCD为长方形 ∴∠EDB=∠DBC（2分） ∴∠EDB=∠EBD，‎ ‎∴△BED为等腰三角形（3分）‎ ‎（2）设AE=，则BE=ED=8－（4分）‎ ‎ 在Rt△BAE中，BE2=AB2+AE2, ∴（8－）2=22+2（6分）‎ 解得：= ∴AE的长为（7分）‎ ‎24. （1）设线段AB的表达式为=（1≤≤2）（1分）‎ ‎ 把A（1，60） B（2，170）代入=得 ‎ 解得 ‎ ∴ 线段AB的表达式为=110－50（1≤≤2）（3分）‎ ‎（2）同（1）的求法可得线段BC的方程为：=60+50（2≤≤3）（4分）‎ ‎ 把=182代入=60+50得=2.2（6分）‎ 答：他们离家182km时，共用了2.2小时（7分）‎ ‎25.（1） ∵ Rt△ABC≌Rt△DBE ∴ BC=BE，又BF=BF，∠BCA=∠BEF=90o ‎ ∴ Rt△BCF≌Rt△BEF ∴ CF=EF（3分）‎ （2） 同（1），CF=EF仍然成立 ∴ AF+EF=AC 又 ∵ △BCA≌△BED 八年级 数学 第10页（共10页）‎ ‎∴ AC=DE ∴ AF+EF=DE（5分）‎ （3） ‎（2）中结论不成立（6分），应为：AF=DE+EF（7分）‎ 八年级 数学 第10页（共10页）‎