2020年八年级数学下册10微专题一次函数的实际应用—路程、工程问题习题（新版）冀教版

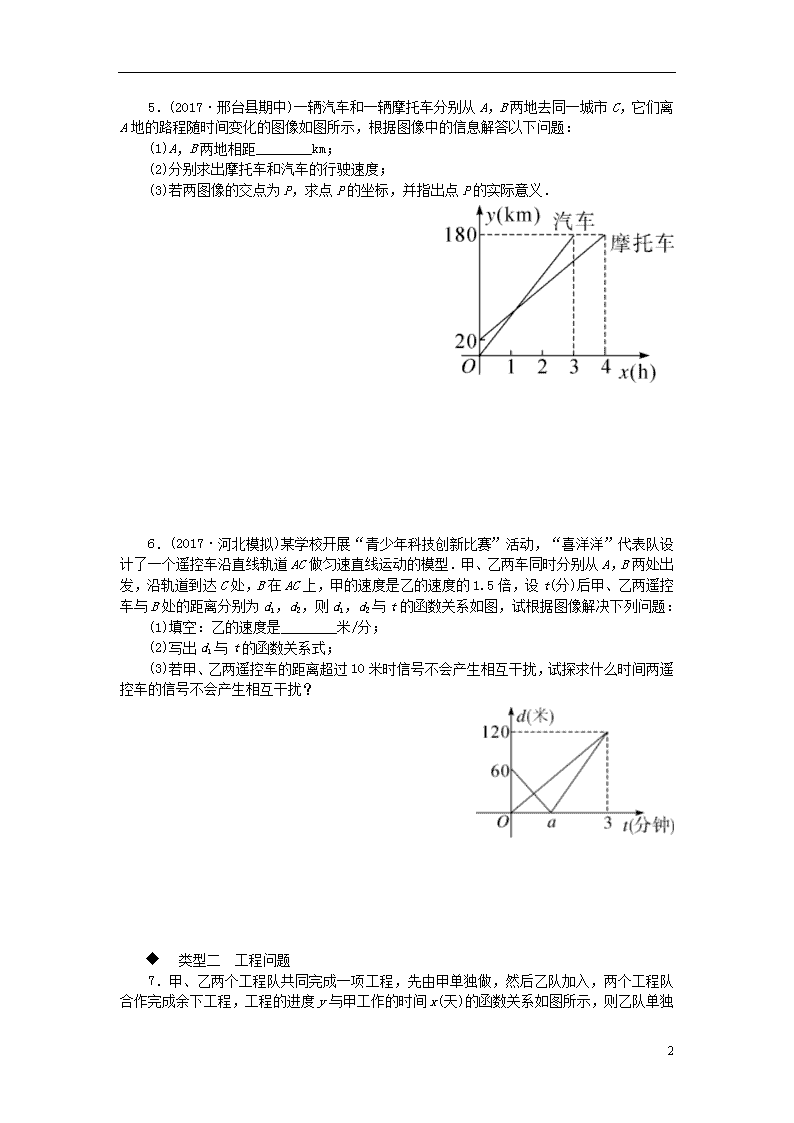
2020年八年级数学下册10微专题一次函数的实际应用—路程、工程问题习题（新版）冀教版

微专题：一次函数的实际应用——路程、工程问题 类型一　路程问题 ‎1．现有甲、乙两支解放军小分队将救灾物资送往某灾区小镇，从部队基地到该小镇只有唯一通道，且路程长为‎24km，甲小队先出发，如图是他们行走的路程与时间的函数图像，四位同学观察此函数图像得出有关信息，其中正确的个数为(　　)‎ A．1个 B．2个 C．3个 D．4个 ‎ ‎ ‎ 第1题图 第2题图 ‎2．(2017·辽阳中考)甲、乙两人分别从A，B两地同时出发，相向而行，匀速前往B地、A地，两人相遇时停留了4min，又各自按原速前往目的地，甲、乙两人之间的距离y(m)与甲所用时间x(min)之间的函数关系如图所示．有下列说法：①A，B之间的距离为‎1200m；②乙行走的速度是甲的1.5倍；③b＝960; ④a＝34.以上结论正确的有(　　)‎ A．①② B．①②③ C．①③④ D．①②④‎ ‎3．(2017·南充中考)小明从家到图书馆看报然后返回，他离家的距离y(km)与离家的时间x(min)之间的对应关系如图所示．如果小明在图书馆看报30min，那么他离家50min时离家的距离为________km.‎ ‎ ‎ 第3题图 第4题图 ‎4．(2017·达州中考)甲、乙两动点分别从线段AB的两端点同时出发，甲从点A出发，向终点B运动，乙从点B出发，向终点A运动．已知线段AB长为‎90cm，甲的速度为‎2.5cm/s.设运动时间为x(s)，甲、乙两点之间的距离为y(cm)，y与x的函数图像如图所示，则图中线段DE所表示的函数关系式为______________________(并写出自变量取值范围)．‎ 4‎ ‎5．(2017·邢台县期中)一辆汽车和一辆摩托车分别从A，B两地去同一城市C，它们离A地的路程随时间变化的图像如图所示，根据图像中的信息解答以下问题：‎ ‎(1)A，B两地相距________km；‎ ‎(2)分别求出摩托车和汽车的行驶速度；‎ ‎(3)若两图像的交点为P，求点P的坐标，并指出点P的实际意义．‎ ‎6．(2017·河北模拟)某学校开展“青少年科技创新比赛”活动，“喜洋洋”代表队设计了一个遥控车沿直线轨道AC做匀速直线运动的模型．甲、乙两车同时分别从A，B两处出发，沿轨道到达C处，B在AC上，甲的速度是乙的速度的1.5倍，设t(分)后甲、乙两遥控车与B处的距离分别为d1，d2，则d1，d2与t的函数关系如图，试根据图像解决下列问题：‎ ‎(1)填空：乙的速度是________米/分；‎ ‎(2)写出d1与t的函数关系式；‎ ‎(3)若甲、乙两遥控车的距离超过‎10米时信号不会产生相互干扰，试探求什么时间两遥控车的信号不会产生相互干扰？‎ 类型二　工程问题 ‎7．甲、乙两个工程队共同完成一项工程，先由甲单独做，然后乙队加入，两个工程队合作完成余下工程，工程的进度y与甲工作的时间x 4‎ ‎(天)的函数关系如图所示，则乙队单独完成此项工程需________天．‎ ‎ ‎ 第7题图 第8题图 ‎8．甲、乙两工程队分别同时开挖两条‎600米长的管道，所挖管道长度y(米)与挖掘时间x(天)之间的关系如图所示，则下列说法中：‎ ‎①甲队每天挖‎100米；‎ ‎②乙队开挖两天后，每天挖‎50米；‎ ‎③甲队比乙队提前3天完成任务；‎ ‎④当x＝2或6时，甲乙两队所挖管道长度都相差‎100米．‎ 正确的有________(填序号)．‎ ‎9．(2017·长春中考)甲、乙两车间同时开始加工一批服装．从开始加工到加工完这批服装甲车间工作了9小时，乙车间在中途停工一段时间维修设备，然后按停工前的工作效率继续加工，直到与甲车间同时完成这批服装的加工任务为止．设甲、乙两车间各自加工服装的数量为y(件)，甲车间加工的时间为x(小时)，y与x之间的函数图像如图所示．‎ ‎(1)甲车间每小时加工服装件数为________件；这批服装的总件数为________件；‎ ‎(2)求乙车间维修设备后，乙车间加工服装数量y与x之间的函数关系式；‎ ‎(3)求甲、乙两车间共同加工完1000件服装时甲车间所用的时间．‎ 4‎ ‎参考答案与解析 ‎1．D ‎ ‎2．D　解析：①当x＝0时，y＝1200，∴A，B之间的距离为‎1200m，结论①正确；②乙的速度为1200÷(24－4)＝60(m/min)，甲的速度为1200÷12－60＝40(m/min)，60÷40＝1.5，∴乙行走的速度是甲的1.5倍，结论②正确；③b＝(60＋40)×(24－4－12)＝800，结论③错误；④a＝1200÷40＋4＝34，结论④正确．故选D.‎ ‎3．0.3‎ ‎4．y＝4.5x－90(20≤x≤36) 　解析：观察图像可知，乙的速度为90÷45＝2(cm/s)，相遇时间为90÷(2.5＋2)＝20(s)，甲到达终点的时间为90÷2.5＝36(s)．∴图中线段DE所表示的函数关系式y＝(2.5＋2)(x－20)＝4.5x－90(20≤x≤36)．‎ ‎5．解：(1)20‎ ‎(2)摩托车的行驶速度为＝40(km/h)，汽车的行驶速度为＝60(km/h)．‎ ‎(3)设摩托车离A地的路程y(km)随时间x(h)变化的函数表达式为y＝kx＋b.将(0，20)，(4，180)代入，得解得即y＝40x＋20.同理可求得汽车离A地的路程y(km)随时间x(h)变化的函数表达式为y＝60x.联立解得则点P的坐标为(1，60)，实际意义：汽车出发后1h，在距离A地‎60km处追上摩托车．‎ ‎6．解：(1)40‎ ‎(2)v甲＝1.5v乙＝1.5×40＝60(米/分)，60÷60＝1(分钟)，∴a＝1，d1＝ ‎(3)易求d2＝40t.当0≤t＜1时，d2＋d1＞10，即－60t＋60＋40t＞10，解得t＜2.5.∵0≤t＜1，∴0≤t＜1，此时两遥控车的信号不会产生相互干扰；当1≤t≤3时，d2－d1＞10，即40t－(60t－60)＞10，解得t＜2.5.∵1≤t≤3，∴1≤t＜2.5，此时两遥控车的信号不会产生相互干扰．综上所述，当0≤t＜2.5时，两遥控车的信号不会产生相互干扰．‎ ‎7．24‎ ‎8．①②④　解析：①根据函数图像得甲队的工作效率为600÷6＝100(米/天)，故①正确；②根据函数图像得乙队开挖两天后的工作效率为(500－300)÷(6－2)＝50(米/天)，故②正确；③乙队完成任务的时间为2＋(600－300)÷50＝8(天)，∴甲队比乙队提前的时间为8－6＝2(天)．故③错误；④当x＝2时，甲队完成的工作量为2×100＝200(米)，乙队完成的工作量为‎300米．当x＝6时，甲队完成的工作量为‎600米，乙队完成的工作量为‎500米．∵300－200＝600－500＝100，∴当x＝2或6时，甲乙两队所挖管道长度都相差‎100米，故④正确．故答案为①②④.‎ ‎9．解：(1)80　1140‎ ‎(2)乙车间每小时加工服装件数为120÷2＝60(件)，乙车间从开始加工到修好设备的时间为9－(420－120)÷60＝4(小时)．∴乙车间维修设备后，乙车间加工服装数量y与x之间的函数关系式为y＝120＋60(x－4)＝60x－120(4≤x≤9)．‎ ‎(3)易知甲车间加工服装数量y与x之间的函数关系式为y＝80x.当80x＋60x－120＝1000时，x＝8.‎ 答：甲、乙两车间共同加工完1000件服装时甲车间所用的时间为8小时．‎ 4‎