2019学年八年级数学下学期期初摸底试题 新人教版新版 人教版

2019学年八年级数学下学期期初摸底试题 新人教版新版 人教版

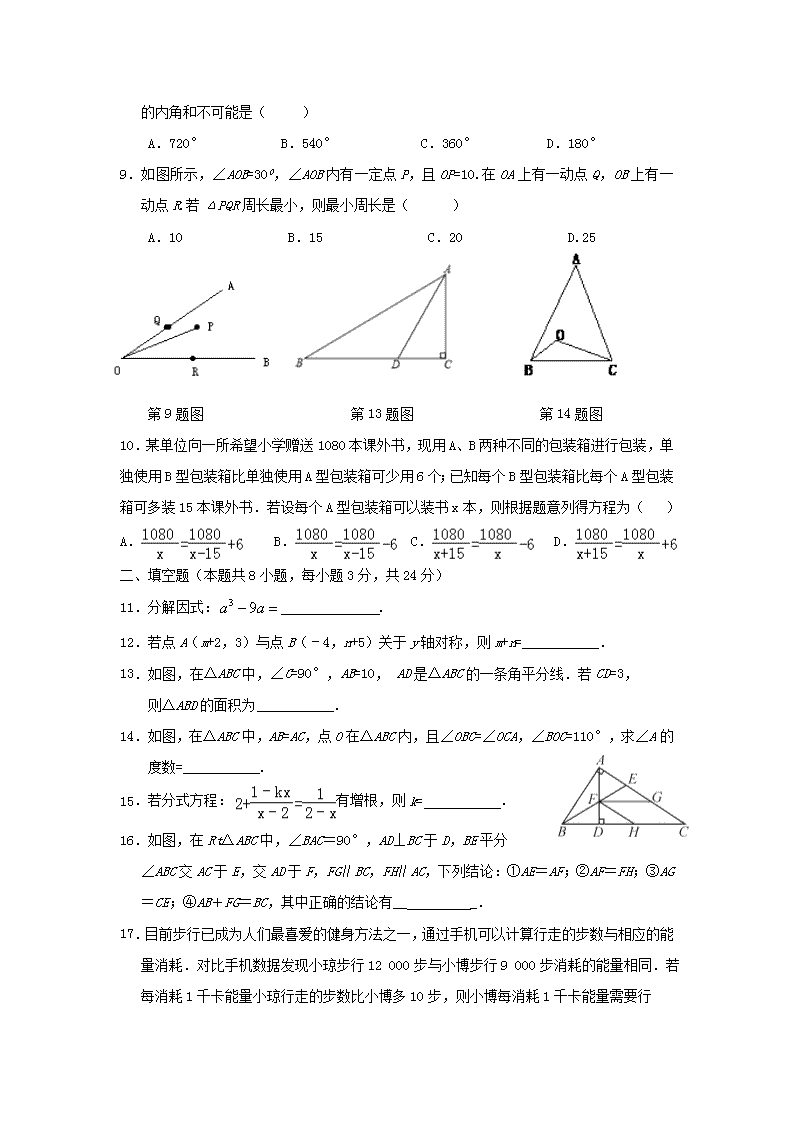
‎2019学年八年级数学下学期期初摸底试题 ‎ ‎ 答卷时间：90 分钟，满分：150分 一、选择题（本题共10小题，每小题3分，共30分）‎ ‎1．下列各式正确的是（ ）.‎ A. B. C. D. ‎ ‎2．在、、、、、中分式的个数有（ ）‎ A. 2个 B. 3个 C. 4个 D. 5个 ‎3．如图，在△ABC和△BDE中，点C在边BD上，边AC交边BE于点F．若AC=BD，AB=ED， BC=BE，则∠ACB等于（ ）‎ A． ∠EDB B． ∠BED C． ∠AFB D． 2∠ABF 第3题图 第4题图 第5题图 ‎ ‎4. 如图，在△ABC中，∠B=∠C=60，点D在AB边上，DE⊥AB，并与AC边交于点E. ‎ 如果AD=1，BC=6，那么CE等于（ ）‎ ‎ A. 5 B. 4 C. 3 D. 2‎ ‎5．如图，锐角三角形ABC中，直线L为BC的中垂线，直线M为∠ABC的角平分线，L与M相交于P点．若∠A=60°，∠ACP=24°，则∠ABP的度数为（ ）‎ ‎ A． 24 B． 30 C． 32 D． 36‎ ‎6.若分式有意义，则的取值范围是（ ）‎ A B. C. D.‎ ‎7．下列各式：①x2﹣10x+25；②x2﹣2x﹣1；③4a2﹣4a﹣1；④﹣m2+m﹣；⑤4x2﹣x2+．‎ 其中不能用完全平方公式分解的个数为（　 　）‎ ‎　 A． 1个　　　　B． 2个　　　　　 C． 3个 　　　　　　D． 4个 ‎8．把一张形状是矩形的纸片剪去其中某一个角，剩下的部分是一个多边形，则这个多边形的内角和不可能是（ ）‎ A．720° B．540° C．360° D．180°‎ ‎9．如图所示，∠AOB=30O，∠AOB内有一定点P，且OP=10.在OA上有一动点Q，OB上有一动点R.若ΔPQR周长最小，则最小周长是（ ）‎ A．10 B．15 C．20 D.25‎ ‎ 第9题图 第13题图 第14题图 ‎ ‎10．某单位向一所希望小学赠送1080本课外书，现用A、B两种不同的包装箱进行包装，单独使用B型包装箱比单独使用A型包装箱可少用6个；已知每个B型包装箱比每个A型包装箱可多装15本课外书．若设每个A型包装箱可以装书x本，则根据题意列得方程为（ ）‎ A． B． C． D．‎ 二、 填空题（本题共8小题，每小题3分，共24分）‎ ‎11．分解因式： .‎ ‎12．若点A（m+2，3）与点B（﹣4，n+5）关于y轴对称，则m+n=___________．‎ ‎13．如图，在△ABC中，∠C=90°，AB=10， AD是△ABC的一条角平分线．若CD=3，‎ 则△ABD的面积为 _________ ．‎ ‎14．如图，在△ABC中，AB=AC，点O在△ABC内，且 ∠OBC=∠OCA，∠BOC=110°，求∠A的度数=___________.‎ ‎15．若分式方程：有增根，则k= ．‎ ‎16．如图，在Rt△ABC中，∠BAC＝90°，AD⊥BC于D，BE平分 ‎∠ABC交AC于E，交AD于F，FG∥BC，FH∥AC，下列结论：①AE＝AF；②AF＝FH；③AG＝CE；④AB＋FG＝BC，其中正确的结论有__ _．‎ ‎17．目前步行已成为人们最喜爱的健身方法之一，通过手机可以计算行走的步数与相应的能量消耗．对比手机数据发现小琼步行12 000步与小博步行9 000步消耗的能量相同．若每消耗1千卡能量小琼行走的步数比小博多10步，则小博每消耗1千卡能量需要行 走 步．‎ ‎18. 对于实数定义运算如下：，例如:,‎ 计算[22]×[32]=_____________.‎ 三、解答题（本题共10小题，共96分）‎ ‎19、（10分）用乘法公式计算 ‎ （1）； （2）‎ ‎20、（10分）（1）因式分解 a（n-1）2-2a（n-1）+a． （2）解方程：‎ ‎21.（8分）先化简，再求值：（﹣）÷，在﹣2，0，1，2四个数中选一个合适的代入求值．‎ ‎ ‎ ‎22. （10分）在等边△ABC中，AO是角平分线，D为AO上一点，以CD为一边，在CD下方作等边△CDE，连接BE.‎ ‎（1）求证：△ACD≌△BCE；‎ ‎（2）过点C作CH⊥BE，交BE的延长线于H，若BC＝8，求CH的长．‎ ‎23. （6分）如图，已知：AD是△ABC的角平分线，CE是△ABC的高，∠BAC=60°，∠BCE=40°，求∠ADB的度数．‎ ‎24. （8分）如图，某市有一块长为（3a+b）米，宽为（2a+b）米的长方形地块，规划部门计划将阴影部分进行绿化，中间将修建一座雕像，则绿化的面积是多少平方米？并求出当a=3，b=2时的绿化面积．‎ ‎25．（8分）作图题： ‎ ‎（1）如图，在△ABC中，AB=3，AC=4，BC=5，EF垂直且平分 BC，点P在直线EF上，直接写出PA+PB的最小值，回答 PA+PB取最小值时点P的位置并在图中标出来；‎ 解：PA+PB的最小值为 ，PA+PB取最小值时点P的 位置是 ；‎ ‎（2）如图3，点M，N分别在直线AB两侧，在直线AB上找一点P，使得.要求画图，并简要叙述确定点P位置的步骤.（无需尺规作图，保留画图痕迹，无需证明）‎ ‎26. （10分）阅读下列材料：‎ 小铭和小雨在学习过程中有如下一段对话：‎ 小铭：“我知道一般当m≠n时，≠.可是我见到有这样一个神奇的等式：‎ ‎=（其中a，b为任意实数，且b≠0）.你相信它成立吗？”‎ 小雨：“我可以先给a，b取几组特殊值验证一下看看.”‎ 完成下列任务： ‎ ‎（1）请选择两组你喜欢的、合适的a，b的值，分别代入阅读材料中的等式，写出代入后得到的具体等式并验证它们是否成立（在相应方框内打勾）；‎ ‎ ① 当a= ，b= 时，等式 （□成立；□不成立）；‎ ‎② 当a= ，b= 时，等式 （□成立；□不成立）.‎ ‎ （2）对于任意实数a，b（b≠0），通过计算说明=是否成立.‎ ‎27. （12分）荣庆公司计划从商店购买同一品牌的台灯和手电筒，已知购买一个台灯比购买一个手电筒多用20元，若用400元购买台灯和用160元购买手电筒，则购买台灯的个数是购买手电筒个数的一半．‎ ‎（1）求购买该品牌一个台灯、一个手电筒各需要多少元？‎ ‎（2）经商谈，商店给予荣庆公司购买一个该品牌台灯赠送一个该品牌手电筒的优惠，如果荣庆公司需要手电筒的个数是台灯个数的2倍还多8个，且该公司购买台灯和手电筒的总费用不超过670元，那么荣庆公司最多可购买多少个该品牌台灯？‎ ‎28.（14分）在等腰Rt△ABC中，∠BAC＝90°，AB＝AC，点A，点B分别是y轴，x轴上两个动点，直角边AC交x轴于点D，斜边BC交y轴于点E.‎ ‎（1）如图①，已知C点的横坐标为－1，直接写出点A的坐标；‎ ‎（2）如图②，当等腰Rt△ABC运动到使点D恰为AC中点时，连接DE，‎ 求证：∠ADB＝∠CDE；‎ ‎（3）如图③，若点A在x轴上，且A(－4，0)，点B在y轴的正半轴上运动时，分别以OB，AB为直角边在第一、二象限作等腰直角△BOD和等腰直角△ABC，连接CD交y轴于点P，问当点B在y轴的正半轴上运动时，BP的长度是否变化？若变化请说明理由，若不变化，请求出BP的长度．‎ 八年级数学寒假作业检测卷参考答案 一、选择题（每小题3分）‎ ‎ 1.B 2. B 3. C 4. B 5. D 6. B 7. C 8. D 9.A 10. C 二． 填空题 （每小题3分）‎ ‎11. a(a+3)(a-3) 12.0 13.15 14.40° ‎ ‎15.K=2 16.①②③④ 17.30 18.9/4‎ 三、 解答题（共96分）‎ 19. ‎(1) 解：原式= ‎ ‎ = .................3分 ‎ =1000000-4 ‎ ‎ =999996 .................5分 ‎ ‎ ‎（2） 解：原式= .................8分 ‎ = .................10分 20. ‎(1) 解：原式= ‎ ‎ = ‎ ‎ = .................5分 ‎ （2） 解： .................9分 ‎ 经检验 是原方程的解.................10分 21. ‎.解：原式=•‎ ‎ ‎ ‎ =2x+8， .................5分 ‎ 当x=1时，原式=2+8=10．.................8分 ‎22.解（1）证明：∵△ABC和△CDE都是等边三角形，‎ ‎∴CA=CB，CD=CE，∠ACB=60°，∠DCE=60°，‎ ‎∴∠ACD+∠BCD=∠ACB=60°，∠BCE+∠BCD=∠DCE=60°，‎ ‎∴∠ACD=∠BCE．‎ 在△ACD和△BCE中，‎ ‎，‎ ‎∴△ACD≌△BCE（SAS）； .................5分 ‎（2）解：∵△ABC是等边三角形，AO是BC边上的高，‎ ‎∴∠BAC=60°，且AO平分∠BAC，‎ ‎∴∠CAD=∠BAC=×60°=30°．‎ ‎∵△ACD≌△BCE，‎ ‎∴∠CAD=∠CBE，‎ ‎∴∠CBE=30°．‎ 又∵CH⊥BE，BC=8，‎ ‎∴在Rt△BCH中，CH=BC=×8=4，即CH=4． .................10分 ‎23. 解：∵AD是△ABC的角平分线，∠BAC=60°，‎ ‎∴∠DAC=∠BAD=30°，‎ ‎∵CE是△ABC的高，∠BCE=40°，‎ ‎∴∠B=50°，‎ ‎∴∠ADB=180°﹣∠B﹣∠BAD=180°﹣30°﹣50°=100°．................ .6分 ‎24.解：阴影部分的面积=（3a+b）（2a+b）﹣（a+b）2‎ ‎=6a2+5ab+b2﹣a2﹣2ab﹣b2‎ ‎=5a2+3ab， .................5分 当a=3，b=2时，原式=5×32+3×3×2=63．.................8分 ‎25.解：（1）4（2分），直线EF与AC边的交点（4分），‎ ‎ （2）先画点M关于直线AB的对称点，射线 与直线AB的交点即为点P. （见图3）‎ ‎………………………………… 8分 ‎26. （1）例如：‎ ‎①当a= 2 ，b= 3 时，等式成立；…………………………… 3分 ‎② 当a= 3 ，b= 5 时，等式成立. ……………………………6分 ‎（2）解：，…………………… 7分 ‎. …………………………… 8分 所以等式=成立.…………………………………… 10分 ‎ ‎27.解：（1）设购买该品牌一个手电筒需要x元，则购买一个台灯需要（x+20）元．‎ 根据题意 得 =×. ................4分 ‎ 解得 x=5 .................5分 ‎ 经检验，x=5是原方程的解．‎ ‎ 所以 x+20=25． .................6分 ‎ 答：购买一个台灯需要25元，购买一个手电筒需要5元；‎ ‎（2）设公司购买台灯的个数为a，则还需要购买手电筒的个数是（2a+8）‎ 由题意得 25a+5（2a+8）≤670‎ ‎ 解得 a≤18 .................12分 所以 荣庆公司最多可购买18个该品牌的台灯．www.czsx.com.cn ‎28.解：（1）如图（1），过点C作CF⊥y轴于点F，‎ ‎∵CF⊥y轴于点F，‎ ‎∴∠CFA=90°，∠ACF+∠CAF=90°，‎ ‎∵∠CAB=90°，‎ ‎∴∠CAF+∠BAO=90°，‎ ‎∴∠ACF=∠BAO，‎ 在△ACF和△ABO中，‎ ‎，‎ ‎∴△ACF≌△ABO（AAS），‎ ‎∴CF=OA=1，‎ ‎∴A（0，1）； .4分 ‎（2）如图2，过点C作CG⊥AC交y轴于点G，‎ ‎∵CG⊥AC，‎ ‎∴∠ACG=90°，∠CAG+∠AGC=90°，‎ ‎∵∠AOD=90°，‎ ‎∴∠ADO+∠DAO=90°，‎ ‎∴∠AGC=∠ADO，‎ 在△ACG和△ABD中，，‎ ‎∴△ACG≌△ABD（AAS），‎ ‎∴CG=AD=CD，∠ADB=∠G，‎ ‎∵∠ACB=45°，∠ACG=90°，‎ ‎∴∠DCE=∠GCE=45°，‎ 在△DCE和△GCE中，‎ ‎，‎ ‎∴△DCE≌△GCE（SAS），‎ ‎∴∠CDE=∠G，‎ ‎∴∠ADB=∠CDE； .4分 ‎（3）BP的长度不变，理由如下：‎ 如图（3），过点C作CE⊥y轴于点E．‎ ‎∵∠BAC=90°，‎ ‎∴∠CBE+∠ABO=90°．‎ ‎∵∠BAO+∠ABO=90°，‎ ‎∴∠CBE=∠BAO．‎ ‎∵∠CEB=∠AOB=90°，AB=AC，‎ ‎∴△CBE≌△BAO（AAS），‎ ‎∴CE=BO，BE=AO=4．‎ ‎∵BD=BO，‎ ‎∴CE=BD．‎ ‎∵∠CEP=∠DBP=90°，∠CPE=∠DPB，‎ ‎∴△CPE≌△DPB（AAS），‎ ‎∴BP=EP=2． .6分