2020八年级数学上册第1章三角形的初步知识1

2020八年级数学上册第1章三角形的初步知识1

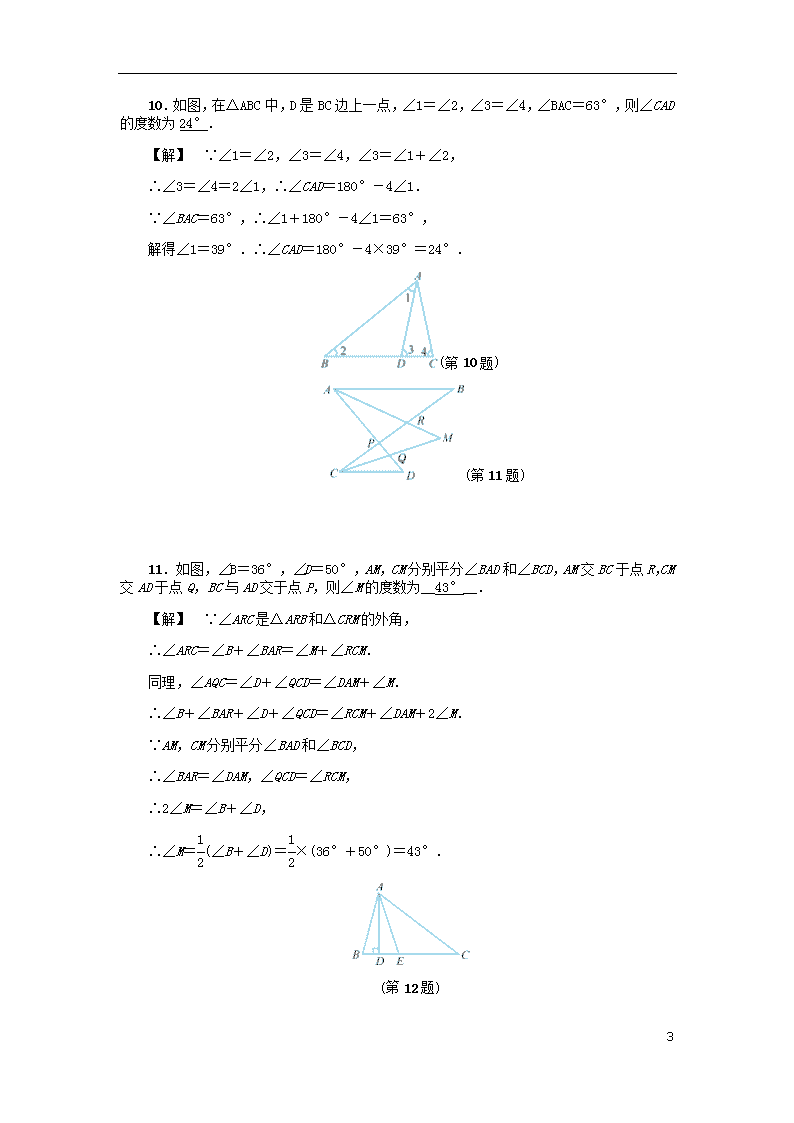
‎1.3 证明（二）‎ A组 ‎1．如图，∠ACD＝120°，∠B＝20°，则∠A的度数为(C)‎ A． 120° B． 90°‎ C． 100° D． 30°‎ ‎,(第1题))　　,(第2题))‎ ‎2．如图，CE是△ABC的外角∠ACD的平分线．若∠B＝35°，∠ACE＝60°，则∠A的度数为(C)‎ A．35° B．95°‎ C．85° D．75°‎ ‎3．如图，平面上直线a，b分别过线段OK的两端点，则a，b相交所成的锐角是(A)‎ A． 60°　　　B． 30°　　　C． 70°　　　D． 8°‎ ‎,(第3题))　　,(第4题))‎ ‎4．如图，直线AB∥CD，∠A＝70°，∠C＝40°，则∠E等于(A)‎ A． 30°　　　B． 40°　　　C． 60°　　　D． 70°‎ ‎5．若三角形的三个外角的度数之比为2∶3∶4，则与之对应的三个内角的度数之比为(C)‎ A． 4∶3∶2　　 B． 3∶2∶4‎ C． 5∶3∶1　　 D． 3∶1∶5‎ ‎6．如图，l1∥l2，则下列式子成立的是(B)‎ A．∠α＋∠β＋∠γ＝180° ‎ B．∠α＋∠β－∠γ＝180°‎ C．∠β＋∠γ－∠α＝180° ‎ D．∠α－∠β＋∠γ＝180°‎ ‎,(第6题))　　,(第7题))‎ 4‎ ‎7．如图，点A，C，F，B在同一条直线上，CD平分∠ECB，FG∥CD．若∠ECA的度数为α，则∠GFB＝90°－(用含α的代数式表示)．‎ ‎(第8题)‎ ‎8．如图，已知D为△ABC的边BC的延长线上一点，DF⊥AB于点F，且交AC于点E，∠A＝34°，∠D＝42°．求∠ACD的度数．‎ ‎【解】　∵DF⊥AB，‎ ‎∴∠BFD＝90°．‎ ‎∵∠BDF＋∠B＋∠D＝180°，‎ ‎∴∠B＝180°－∠BFD－∠D＝180°－90°－42°＝48°，∴∠ACD＝∠A＋∠B＝34°＋48°＝82°．‎ B组 ‎9．如图，∠1，∠2，∠3，∠4的数量关系为(A)‎ ‎(第9题)‎ A． ∠1＋∠2＝∠4－∠3‎ B． ∠1＋∠2＝∠3＋∠4‎ C． ∠1－∠2＝∠4－∠3‎ D． ∠1－∠2＝∠3－∠4‎ ‎【解】　∵∠AEF是△BED的外角，‎ ‎∴∠AEF＝∠2＋∠3．‎ ‎∵∠4是△AEF的外角，∴∠4＝∠1＋∠AEF，‎ ‎∴∠4＝∠1＋∠2＋∠3，‎ ‎∴∠1＋∠2＝∠4－∠3．‎ 4‎ ‎10．如图，在△ABC中，D是BC边上一点，∠1＝∠2，∠3＝∠4，∠BAC＝63°，则∠CAD的度数为24°．‎ ‎【解】　∵∠1＝∠2，∠3＝∠4，∠3＝∠1＋∠2，‎ ‎∴∠3＝∠4＝2∠1，∴∠CAD＝180°－4∠1．‎ ‎∵∠BAC＝63°，∴∠1＋180°－4∠1＝63°，‎ 解得∠1＝39°．∴∠CAD＝180°－4×39°＝24°．‎ ‎(第10题)‎ ‎　　(第11题)‎ ‎11．如图，∠B＝36°，∠D＝50°，AM，CM分别平分∠BAD和∠BCD，AM交BC于点R，CM交AD于点Q，BC与AD交于点P，则∠M的度数为__43°__．‎ ‎【解】　∵∠ARC是△ARB和△CRM的外角，‎ ‎∴∠ARC＝∠B＋∠BAR＝∠M＋∠RCM．‎ 同理，∠AQC＝∠D＋∠QCD＝∠DAM＋∠M．‎ ‎∴∠B＋∠BAR＋∠D＋∠QCD＝∠RCM＋∠DAM＋2∠M．‎ ‎∵AM，CM分别平分∠BAD和∠BCD，‎ ‎∴∠BAR＝∠DAM，∠QCD＝∠RCM，‎ ‎∴2∠M＝∠B＋∠D，‎ ‎∴∠M＝(∠B＋∠D)＝×(36°＋50°)＝43°．‎ ‎(第12题)‎ 4‎ ‎12．已知：如图，在△ABC中，∠B>∠C，AE为∠BAC的平分线，AD⊥BC于点D．求证：∠DAE＝(∠B－∠C)．‎ ‎【解】　∵AE为∠BAC的平分线，‎ ‎∴∠BAE＝∠BAC＝(180°－∠B－∠C)．‎ ‎∵AD⊥BC，∴∠BAD＝90°－∠B，‎ ‎∴∠DAE＝∠BAE－∠BAD＝(180°－∠B－∠C)－(90°－∠B)＝(∠B－∠C)．‎ 数学乐园 ‎(第13题)‎ ‎13．如图，∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠G＝__540°__．‎ 导学号：91354003‎ ‎【解】　连结DG，AC，DF．‎ ‎∵∠BAG＝∠CAG＋∠BAC，∠BCD＝∠ACB＋∠ACD，∠CDE＝∠CDF＋∠EDF，∠EFG＝∠DFE＋∠DFG，∠CAG＋∠ACD＝∠CDG＋∠AGD，∴∠BAG＋∠B＋∠BCD＋∠CDE＋∠E＋∠EFG＋∠AGF＝∠GAC＋∠BAC＋∠B＋∠ACB＋∠ACD＋∠CDF＋∠EDF＋∠E＋∠DFE＋∠DFG＋∠AGF＝(∠BAC＋∠B＋∠ACB)＋(∠CAG＋∠ACD＋∠CDF＋∠DFG＋∠AGF)＋(∠EDF＋∠E＋∠DFE)＝180°＋(∠CDG＋∠AGD＋∠CDF＋∠DFG＋∠AGF)＋180°＝180°＋180°＋180°＝540°．‎ 4‎