- 2021-11-01 发布 |
- 37.5 KB |
- 16页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
八年级上数学课件《全等三角形》 (16)_苏科版
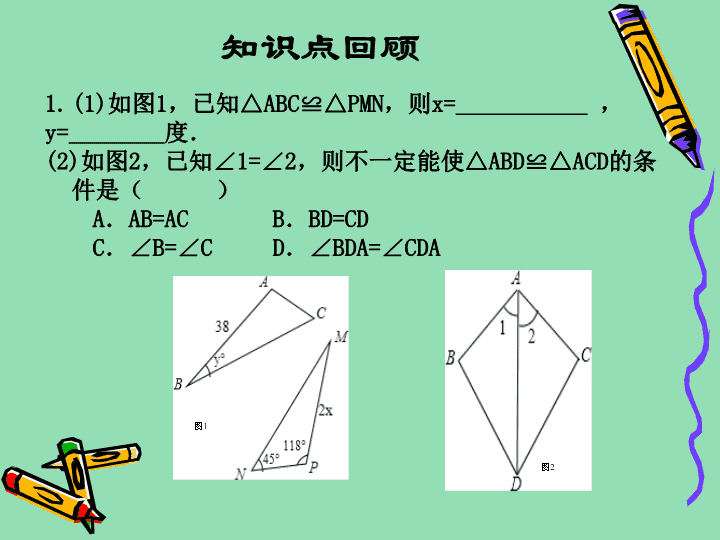
知识点回顾 1.(1)如图1,已知△ABC≌△PMN,则x= , y= 度. (2)如图2,已知∠1=∠2,则不一定能使△ABD≌△ACD的 条件是( ) A.AB=AC B.BD=CD C.∠B=∠C D.∠BDA=∠CDA 图1 图2 探索活动 请同学们将课前准备好的两个全等的三角形拿出 来,然后任意的组合(可以将一边重合、错开, 可以将一个顶点重合……),进行不同的“平移、 旋转、翻折”变换,你能得到哪些图形呢? …… 探究性问题:若∠BAD=∠CAD,则添加什么条 件可得△ABD≌ △ACD? (1)边角边方案:添加 AB=AC (2)角边角方案:添加∠ADB=∠ADC (3)角角边方案:添加∠B=∠C (通过看图,挖掘图中的隐含条件) B A C D 挖掘“隐含条件”判全等 1.如图,AB=AC,BE和CD相交于P,AD=AE。 说明:∠B=∠C. A B C D E P 解:在△ABE和△ACD中 AB=AC(已知) ∠ A= ∠ A(公共角) AE=AD(已知) ∴△ABE ≌ △ACD(SAS) ∴ ∠B=∠C(全等三角形对应角相等) 变式一: 如图,AB=AC,BE和CD相交于P,BD=CE, 说明:∠B=∠C A B C D E P 解:∵AB=AC,BD=CE ∴ AB-BD=AC-CE 即AD=AE ∴在△ABE和△ACD中 AB=AC(已知) ∠ A= ∠ A(公共角) AE=AD(已证) ∴△ABE ≌ △ACD(SAS) ∴∠B=∠C (全等三角形对应角相等) 挖掘“隐含条件”判全等 变式二: 如图,AB=AC,BE和CD相交于P,BP=CP, 说明:∠B=∠C. 适当添加辅助线 解:连接AP 在△ABP和△ACP中 AB=AC(已知) AP=AP(公共边) BP=CP(已知) ∴△ABP ≌ △ACP(SSS) ∴ ∠B=∠C(全等三角形对应角相等) 挖掘“隐含条件”判全等 A B C D E P 如图,下面四个条件中,请你选择两个作为已 知条件,再从剩下的两个当中选择一个作为结论, 写出一个正确的论断,并写出这个论断正确的理 由. ①AC=BD;②AD=BC;③∠CAB=∠DBA;④OC=OD. ①② → ③ ①② → ④ ①③ → ④ ②④ → ③ A B DC O 如图,CE⊥AB,DF⊥AB,垂足分别为E、F,且 AE=BF,∠C=∠D, 则(1)△ADF和△BEC全等吗?为什么? (2)图中还有那些全等的三角形?你能再找 出一对来证明吗? M N C D E F A B O 1.要测量河两岸相对的两点A、B的距离,先在AB的 垂线BF上取两点C、D,使CD =BC,再定出BF的垂线DE, 使A、C、E在一条直线上,可以证明△EDC≌△ABC, 得到ED=AB,因此测得ED的长就是AB的长(如图),判定 △EDC≌△ABC的理由是( ) A.边角边 B.角边角 C.边边边 D.斜边-直角边 B 2.如图,有一湖的湖岸在A、B之间呈一段圆弧 状,A、B间的距离不能直接测得.你能用已学 过的知识或方法设计测量方案,求出A、B间的 距离吗? 3.你能按以下图形,编一个题目给你的同 桌吗? A B C D E 1.你有什么收获? 2.你还有哪些疑惑? 课本P127 2、3、4、5、6 = = 两边和其中一边的对角对应相等的 两个三角形不一定全等查看更多