- 2021-10-27 发布 |
- 37.5 KB |
- 16页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
人教版八年级上册数学同步练习课件-第11章-三角形 复习与巩固11
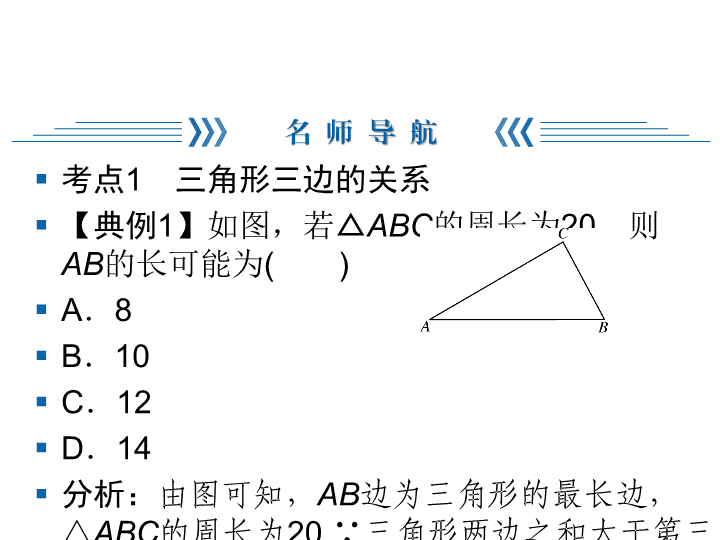
《三角形》复习与巩固 § 考点1 三角形三边的关系 § 【典例1】如图,若△ABC的周长为20,则 AB的长可能为( ) § A.8 § B.10 § C.12 § D.14 § 分析:由图可知,AB边为三角形的最长边, △ABC的周长为20.∵三角形两边之和大于第 三边,∴AB的长小于10. § 答案:A 2 § 考点2 与三角形有关的角的计算 § 【典例2】如图,△ABC中,∠A=30°, ∠B=62°,CE平分∠ACB,CD⊥AB于点 D,DF⊥CE于点F,求∠CDF的度数. § 分析:若想求∠CDF的度数,则可求∠CDF 的余角∠FCD,∠FCD=∠FCB-∠DCB.又 ∠FCB是∠ACB的一半,∠ACB可利用 △ABC的内角和定理求出;∠DCB可通过 ∠B的余角求出.这样就可求出∠CDF的度 数. 3 4 § 考点3 三角形外角性质的应用 § 【典例3】如图,已知D是△ABC边BC延长 线上一点,DF⊥AB于点F,交AC于点E, ∠A=35°,∠D=42°.求: § (1)∠ACD的度数; § (2)∠AEF的度数. § 分析:(1)若想求∠ACD的度数,则可由 ∠ACD是△ABC的外角求得,即∠ACD= ∠B+∠A,其中∠B通过是∠D的余角求得; (2)若想求∠AEF的度数,可由△AEF的内角 和求得. 5 § 解答:(1)∵DF⊥AB,∴∠B=90°-∠D= 48°. § ∵∠ACD是△ABC的一个外角,∴∠ACD= ∠A+∠B=83°. § (2)∵DF⊥AB,∴∠AFD=90°,∴∠AEF =90°-∠A=55°. 6 § 考点4 多边形内、外角和的应用 § 【典例4】正多边形的一个内角的度数恰好等 于它的相邻外角的度数的3倍,则这个正多边 形的边数为________. § 分析:设正多边形的一个外角等于x°. § ∵正多边形一个内角的度数恰好等于它的外 角的度数的3倍, § ∴这个正多边形的一个内角为3x°, § ∴x+3x=180,解得x=45. § ∴这个多边形的边数是360°÷45°=8. § 答案:8 7 § ★考点1 三角形三边的关系 § 1.一个等腰三角形一边长为4 cm,另一边 长为5 cm,那么这个等腰三角形的周长是( ) § A.13 cm B.14 cm § C.13 cm或14 cm D.以上都不对 8 C § 2.已知三角形三边长分别为2,x,13,若x为 正整数,则这样的三角形个数为 § ( ) § A.2 B.3 § C.5 D.13 § 解析:∵11<x<15,且x为整数,则x= 12,13,14,∴有3个三角形. § 3.已知三角形三边长分别为a、b、c,其中 a、b满足(a-6)2+|b-8|=0,求这个三角形 最长边c的取值范围. § 解:∵(a-6)2+|b-8|=0,∴a-6=0,b- 8=0,∴a=6,b=8.∵这个三角形的最长 边为c,∴b查看更多
相关文章
- 当前文档收益归属上传用户