2018-2019学年河北保定八年级上数学期中试卷
2018-2019学年河北保定八年级上数学期中试卷
一、选择题
1. 下列各组数中,是勾股数的是( )
A.12,8,5 B.30,40,50 C.9,13,15 D.16,18,110
2. 在下列各数中是无理数的有( )
−(−5)2、36、17、0、−π、311、3.1415、15、2.010101…(相邻两个1之间有1个0).
A.1个 B.2个 C.3个 D.4个
3. 下列计算正确的是( )
A.20=210 B.(−3)2=−3 C.4−2=2 D.2⋅3=6
4. 已知直角三角形的两边长分别为3和4,则此三角形的周长为( )
A.12 B.7+7 C.12或7+7 D.以上都不对
5. 下列说法中错误的是( )
A.9的算术平方根是3 B.16的平方根是±2
C.27的立方根为±3 D.立方根等于1的数是1
6. 414、226、15三个数的大小关系是( )
A.414<15<226 B.226<15<414 C.414<226<15 D.226<414<15
7. 下列函数中,一次函数为( )
A.y=x3 B.y=−2x+1 C.y=2x D.y=2x2+1
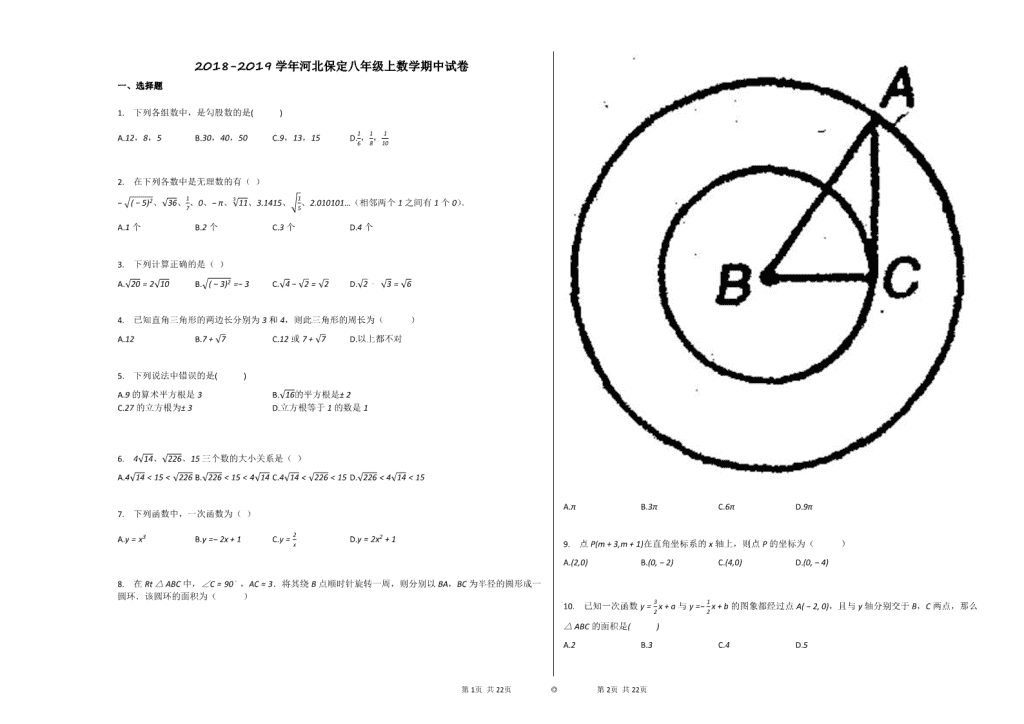
8. 在Rt△ABC中,∠C=90∘,AC=3.将其绕B点顺时针旋转一周,则分别以BA,BC为半径的圆形成一圆环.该圆环的面积为( )
A.π B.3π C.6π D.9π
9. 点P(m+3,m+1)在直角坐标系的x轴上,则点P的坐标为( )
A.(2,0) B.(0,−2) C.(4,0) D.(0,−4)
10. 已知一次函数y=32x+a与y=−12x+b的图象都经过点A(−2, 0),且与y轴分别交于B,C两点,那么△ABC的面积是( )
A.2 B.3 C.4 D.5
第21页 共22页 ◎ 第22页 共22页
11. 如图:一个三级台阶,它的每一级的长,宽和高分别是50cm,30cm,10cm,A和B是这个台阶的两个相对的端点,A点上有一只壁虎,它想到B点去吃可口的食物,请你想一想,这只壁虎从A点出发,沿着台阶面爬到B点,最短路线的长是多少( )
A.13cm B.40cm C.130cm D.169cm
12. 正比例函数y=kx(k≠0)函数值y随x的增大而增大,则y=kx−k的图象大致是( )
A. B. C. D.
13. 已知函数y=(m+1)xm2−3是正比例函数,且图象在第二、四象限内,则m的值是( )
A.2 B.−2 C.±2 D.12
14. 对于任意的正数m、n定义运算※为:m※n=m−n(m≥n),m+n(m
b).例如:化简7+43解:首先把7+43化为7+212,这里m=7,n=12;由于4+3=7,4×3=12,即(4)2+(3)2=7 4⋅3=12,∴7+43=7+212=(4+3)2=2+3.
由上述例题的方法化简:
(1)13−242
(2)7−40
(3)2+3
第21页 共22页 ◎ 第22页 共22页
如图,直线y=kx+6与x轴、y轴分别相交于点E、F,点E的坐标为(−8,0),点A的坐标为(−6,0),点P(x,y)是第二象限内的直线上的一个动点.
(1)求k的值;
(2)在点P的运动过程中,写出△OPA的面积S与x的函数表达式,并写出自变量x的取值范围;
(3)探究,当点P运动到什么位置(求P的坐标)时,△OPA的面积是△OEF的面积的三分之二?
第21页 共22页 ◎ 第22页 共22页
参考答案与试题解析
2018-2019学年河北保定八年级上数学期中试卷
一、选择题
1.
【答案】
B
【考点】
勾股数
【解析】
根据勾股定理的逆定理分别进行分析,从而得到答案.
【解答】
解:判断是否为勾股数,必须根据勾股数是正整数,同时还需验证两小边的平方和是否等于最长边的平方.
A,∵ 52+82≠122,∴ 此选项不符合题意;
B,∵ 302+402=502,∴ 此选项符合题意;
C,∵ 92+132≠152,∴ 此选项不符合题意;
D,∵ (16)2+(18)2≠(110)2,∴ 此选项不符合题意.
故选B.
2.
【答案】
C
【考点】
无理数的判定
【解析】
无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.
【解答】
解:−π、311、15是无理数,
故选:C.
3.
【答案】
D
【考点】
二次根式的相关运算
二次根式的性质与化简
【解析】
结合二次根式加减法的运算法则进行求解即可.
【解答】
A、20=25≠210,本选项错误;
B、(−3)2=3≠−3,本选项错误;
C、4−2≠2,本选项错误;
D、2×3=6,本选项正确.
故选D.
4.
【答案】
C
【考点】
勾股定理
【解析】
先设Rt△ABC的第三边长为x,由于4是直角边还是斜边不能确定,故应分4是斜边或x为斜边两种情况讨论.
【解答】
解:设Rt△ABC的第三边长为x,
①当4为直角三角形的直角边时,x为斜边,
由勾股定理得,x=5,此时这个三角形的周长=3+4+5=12;
②当4为直角三角形的斜边时,x为直角边,
由勾股定理得,x=7,此时这个三角形的周长=3+4+7=7+7.
故选C.
5.
【答案】
C
【考点】
立方根的实际应用
算术平方根
平方根
【解析】
根据算术平方根,平方根,立方根的定义求出每个的值,再判断即可.
【解答】
解:A,9的算术平方根是3,故本选项不符合题意;
B,16的平方根是±2,故本选项不符合题意;
C,27的立方根是3,故本选项符合题意;
D,立方根等于1的数是1,故本选项不符合题意.
故选C.
6.
【答案】
A
【考点】
实数大小比较
【解析】
把第一个数根号外的数移到根号内,第3个数用根式表示出来,然后比较被开方数,被开方数大的数,它本身就大.
【解答】
第21页 共22页 ◎ 第22页 共22页
解:∵ 414=224,
15=225,
224<225<226,
∴ 414<15<226.
故选A.
7.
【答案】
B
【考点】
一次函数的定义
【解析】
根据形如y=kx+b(k≠0,k、b是常数)的函数,叫做一次函数进行分析即可.
【解答】
解:A、不是一次函数,故此选项错误;
B、是一次函数,故此选项正确;
C、不是一次函数,故此选项错误;
D、不是一次函数,故此选项错误;
故选:B.
8.
【答案】
D
【考点】
勾股定理
圆的有关概念
【解析】
本题考查了圆的认识,勾股定理的应用.
【解答】
解:圆环的面积=π⋅AB2−π⋅BC2=π(AB2-BC2),
在直角三角形ABC中,AC2=AB2-BC2,
所以圆环的面积是π⋅AC2=9π.
故选D.
9.
【答案】
A
【考点】
点的坐标
【解析】
本小题考察学生对于点的坐标以及对坐标轴的认知.
【解答】
解:由题意知,点P(m+3,m+1)在直角坐标系的x轴上,则点的纵坐标为0,
可得m+1=0,即m=−1,
∴m+3=−1+3=2.
∴点的横坐标为2.
故选A.
10.
【答案】
C
【考点】
两直线相交非垂直问题
【解析】
可先根据点A的坐标用待定系数法求出a,b的值,即求出两个一次函数的解析式,进而求出它们与y轴的交点,即B,C的坐标.那么三角形ABC中,底边的长应该是B,C纵坐标差的绝对值,高就应该是A点横坐标的绝对值,因此可根据三角形的面积公式求出三角形的面积.
【解答】
解:把点A(−2, 0)代入y=32x+a,
得:a=3,
∴ 点B(0, 3).
把点A(−2, 0)代入y=−12x+b,
得:b=−1,
∴ 点C(0, −1).
∴ BC=|3−(−1)|=4,
∴ S△ABC=12×2×4=4.
故选C.
11.
【答案】
C
【考点】
平面展开-最短路径问题
勾股定理的应用
【解析】
此类题目只需要将其展开便可直观的得出解题思路.将台阶展开得到的是一个矩形,蚂蚁要从B点到A点的最短距离,便是矩形的对角线,利用勾股定理即可解出答案.
【解答】
解:将台阶展开,如图,
因为BC=30×3+10×3=120,AC=50,
所以AB2=AC2+BC2=16900,
所以AB=130cm,
所以壁虎爬行的最短路线的长是130cm.
故选C.
12.
第21页 共22页 ◎ 第22页 共22页
【答案】
B
【考点】
一次函数的图象
正比例函数的性质
【解析】
直接利用正比例函数的性质得出k的取值范围,进而得出一次函数经过的象限.
【解答】
∵ 正比例函数y=kx(k≠0)函数值y随x的增大而增大,
∴ k>0,
∴ y=kx−k的图象经过第一、三、四象限,
13.
【答案】
B
【考点】
正比例函数的性质
正比例函数的定义
【解析】
根据正比例函数的定义得出m2−3=1,m+1<0,进而得出即可.
【解答】
∵ 函数y=(m+1)xm2−3是正比例函数,且图象在第二、四象限内,
∴ m2−3=1,m+1<0,
解得:m=±2,
则m的值是−2.
14.
【答案】
B
【考点】
定义新符号
二次根式的混合运算
【解析】
根据题目所给的运算法则进行求解.
【解答】
解:∵ 3>2,
∴ 3※2=3−2.
∵ 8<12,
∴ 8※12=8+12=2×(2+3),
∴ (3※2)×(8※12)=(3−2)×2×(2+3)=2.
故选B.
15.
【答案】
D
【考点】
勾股定理
等腰三角形的判定与性质
【解析】
首先连接AD,由△ABC中,AB=AC=13,BC=10,D为BC中点,利用等腰三角形的三线合一的性质,即可证得:AD⊥BC,然后利用勾股定理,即可求得AD的长,然后利用面积法来求DE的长.
【解答】
解:连接AD,
∵ △ABC中,AB=AC=13,BC=10,D为BC中点,
∴ AD⊥BC,BD=12BC=5,
∴ AD=AB2−BD2=12,
又∵ DE⊥AB,
∴ 12BD⋅AD=12AB⋅ED,
∴ ED=BD⋅ADAB=5×1213=6013,
故选D.
16.
【答案】
A
【考点】
规律型:点的坐标
【解析】
设第n次跳动至点An,根据部分点An坐标的变化找出变化规律“A4n(−n−1, 2n),A4n+1(−n−1, 2n+1),A4n+2(n+1, 2n+1),A4n+3(n+1, 2n+2)(n为自然数)”,依此规律结合2015=503×4+3即可得出点A2015的坐标.
【解答】
解:设第n次跳动至点An,
观察,发现:A(−1, 0),A1(−1, 1),A2(1, 1),A3(1, 2),A4(−2, 2),A5(−2, 3),A6(2, 3),A7(2, 4),A8(−3, 4),A9(−3, 5),…,
∴ A4n(−n−1, 2n),A4n+1(−n−1, 2n+1),A4n+2(n+1, 2n+1),A4n+3(n+1, 2n+2)(n为自然数).
∵ 2015=503×4+3,
∴ A2015(503+1, 503×2+2),即(504, 1008).
故选A.
二、填空题
【答案】
0,−6
【考点】
坐标与图形变化-平移
关于x轴、y轴对称的点的坐标
第21页 共22页 ◎ 第22页 共22页
【解析】
本题主要考查了已知点的平移以及关于坐标轴的对称点问题,向右平移2个单位,横坐标加2,纵坐标不变,向下平移3个单位,纵坐标减3,横坐标不变,由此可得x+2=2y−3=3,求得P0,6,其对称点P′坐标为0,−6.
【解答】
解:设P点坐标为x,y,
那么向右移动2个单位后的坐标为x+2,y,
再向下移动3个单位后的坐标为x+2,y−3,
根据题意:x+2=2,y−3=3,
∴x=0,y=6,
即P点坐标为0,6,
P关于x轴对称点P′的坐标0,−6.
故答案为:0,−6.
【答案】
−14,4916
【考点】
平方根
【解析】
根据正数的平方根互为相反数,两平方根相加等于0求出a值,再求出一个平方根,平方就可以得到这个正数.
【解答】
解:根据题意,(a+2)+(3a−1)=0,
解得a=−14,
∴ a+2=74,(74)2=4916,
∴ 这个正数是4916.
故答案为−14;4916
【答案】
(32, 0)
【考点】
一次函数图象上点的坐标特点
规律型:点的坐标
【解析】
在Rt△OA1B1中,由OA1=1、A1B1=3OA1=3,利用勾股定理可得出OB1=2,进而可得出点A2的坐标为(2, 0),同理,即可求出点A3、A4、A5、A6的坐标,此题得解.
【解答】
解:在Rt△OA1B1中,OA1=1,A1B1=3OA1=3,
∴ OB1=OA12+A1B12=2,
∴ 点A2的坐标为(2, 0).
同理,可得出:点A3的坐标为(4, 0),点A4的坐标为(8, 0),点A5的坐标为(16, 0),点A6的坐标为(32, 0).
故答案为:(32, 0).
三、解答题
【答案】
解:(1)原式=42×2−5
=8−5
=3.
(2)原式=5−1−2
=2.
(3)原式=75+4−203−5+7
=81−203.
(4)原式=43×(123−2−93)
=43×(33−2)
=36−46.
【考点】
实数的运算
【解析】
(1)本小题考察学生们关于实数的运算.
(2)本小题考察学生们关于实数的运算及二次根式的运算.
(3)本小题考察学生们关于实数的运算,平方差公式和完全平方公式.
(4)本小题考察学生们关于实数的运算及二次根式的化简.
【解答】
解:(1)原式=42×2−5
=8−5
=3.
(2)原式=5−1−2
=2.
(3)原式=75+4−203−5+7
=81−203.
(4)原式=43×(123−2−93)
=43×(33−2)
=36−46.
【答案】
第21页 共22页 ◎ 第22页 共22页
连接AC,
∵ ∠ABC=90∘,AB=4,BC=3,
∴ 根据勾股定理AC=32+42=5(cm),
又∵ CD=12cm,AD=13cm,
∴ AC2+DC2=52+122=169,
AD2=132=169,
根据勾股定理的逆定理:∠ACD=90∘.
∴ 四边形ABCD的面积=S△ABC+S△ACD=12×3×4+12×5×12=36(cm2).
【考点】
三角形的面积
勾股定理
勾股定理的逆定理
【解析】
连接AC,得到直角三角形△ABC,利用勾股定理可以求出AC,根据数据特点,再利用勾股定理逆定理可以得到△ACD也是直角三角形,这样四边形的面积就被分解成了两个直角三角形的面积,代入面积公式就可以求出答案.
【解答】
连接AC,
∵ ∠ABC=90∘,AB=4,BC=3,
∴ 根据勾股定理AC=32+42=5(cm),
又∵ CD=12cm,AD=13cm,
∴ AC2+DC2=52+122=169,
AD2=132=169,
根据勾股定理的逆定理:∠ACD=90∘.
∴ 四边形ABCD的面积=S△ABC+S△ACD=12×3×4+12×5×12=36(cm2).
【答案】
解:(1)根据题意可作出如图所示的坐标系;
(2)如图,△A1B1C1即为所求;
(3)由图可知,B1(2, 1);
(4)S△ABC=3×4−12×2×4−12×2×1−12×2×3=12−4−1−3=4.
【考点】
作图-轴对称变换
【解析】
(1)根据A点坐标建立平面直角坐标系即可;
(2)作出各点关于y轴的对称点,再顺次连接即可;
(3)根据点B1在坐标系中的位置写出其坐标即可;
(4)利用矩形的面积减去三个顶点上三角形的面积即可.
【解答】
解:(1)根据题意可作出如图所示的坐标系;
(2)如图,△A1B1C1即为所求;
(3)由图可知,B1(2, 1);
(4)S△ABC=3×4−12×2×4−12×2×1−12×2×3=12−4−1−3=4.
【答案】
y=0.5x (x≤3000),y=0.8x−900 (x>3000),1660,1400
【考点】
一次函数的综合题
【解析】
第21页 共22页 ◎ 第22页 共22页
首先由股定求斜AC5然后由锐角三角函数的定义sinA=对边斜边,然后相线段的长代入计算即可.
【解答】
解:在R△BC中,∠A=90∘,AB=,BC=4,
∴ inA=BCAC=45.
故答是:45.
【答案】
3,24
2设函数解析式为Q=kt+b,根据图像可知b=36,将(3,6)代入函数解析式得:
6=3k+36,即k=−10,
分析可知Q=−10t+36(0≤t≤3).
3油箱中的油是够用的.
∵ 200÷80=2.5(小时),需用油10×2.5=25L<30L,
∴ 油箱中的油是够用的.
【考点】
一次函数的应用
【解析】
(1)观察图中数据可知,行驶3小时后油箱剩油6L,加油加至30L;
(2)先根据图中数据把每小时用油量求出来,即:(36−6)÷3=10L,再写出函数关系式;
(3)先要求出从加油站到景点需行几小时,然后再求需用多少油,便知是否够用.
【解答】
解:1从图中可知汽车行驶3h后加油,
中途加油30−6=24L.
故答案为:3;24.
2设函数解析式为Q=kt+b,根据图像可知b=36,将(3,6)代入函数解析式得:
6=3k+36,即k=−10,
分析可知Q=−10t+36(0≤t≤3).
3油箱中的油是够用的.
∵ 200÷80=2.5(小时),需用油10×2.5=25L<30L,
∴ 油箱中的油是够用的.
【答案】
解:(1)这里m=6,n=7,由于6+7=13,6×7=42,
即(6)2+(7)2=13,6×7=42
原式=(6−7)2=7−6.
(2)原式=7−210 ,
这里m=5,n=2,
由于2+5=7,2×5=10,即(2)2+(5)2=7,2×5=10,
∴ 7−40=7−210=(5−2)2=5−2.
(3)2+3=2+234,
这里m=32,n=12,
由于32+12=2,,32×12=34,
即322+122=2,32×12=34,
∴ 2+3=2+234=(32+12)2=32+12=62+22.
【考点】
二次根式的应用
【解析】
本题主要考查二次根式的运用,根据题意凑出相关的m,n,再化简二次根式即可.
【解答】
解:(1)这里m=6,n=7,由于6+7=13,6×7=42,
即(6)2+(7)2=13,6×7=42
原式=(6−7)2=7−6.
(2)原式=7−210 ,
这里m=5,n=2,
由于2+5=7,2×5=10,即(2)2+(5)2=7,2×5=10,
∴ 7−40=7−210=(5−2)2=5−2.
(3)2+3=2+234,
这里m=32,n=12,
由于32+12=2,,32×12=34,
即322+122=2,32×12=34,
∴ 2+3=2+234=(32+12)2=32+12=62+22.
【答案】
解:(1)∵直线y=kx+6过点E(−8,0),
∴ 0=−8k+6,
∴ k=34.
(2)∵点A的坐标为(−6,0),
∴ OA=6,
∵点P(x,y)是第二象限内的直线上的一个动点,
∴ΔOPA的面积:S=12×6×(34x+6)=94x+18.
∵94x+18>0,且x<0.
∴ x∈(−8,0)
第21页 共22页 ◎ 第22页 共22页
∴S=94x+18 ,x∈(−8,0).
(3)由函数关系式令x=0,得到y=6.
ΔOEF的面积S=12×8×6=24,
由ΔOPA的面积是ΔOEF的23,得到ΔOPA的面积为S=24×23=16.
令S=94x+18=16,解得x=−89.
当x=−89时,y=34×(−89)+6=163.
所以当点P的坐标为(−89,163)时,ΔOPA的面积为16.
【考点】
一次函数图象与系数的关系
动点问题
一次函数图象与几何变换
一次函数的图象
一次函数的性质
待定系数法求一次函数解析式
【解析】
(1)本题考查了根据已知点的坐标,求一次函数的系数值,只需要将已知点的坐标带入就能解得函数的系数值.
(2)本题主要考察了从坐标系中通过动点P的运动,所得到的面积的变化用函数表达出来.根据三角形的面积公式结合解析式,根据题意求出自变量的取值范围.
(3)根据(2)中得到的S与x的函数关系式,求出面积S.解出方程x的值,再代入直线的解析式求出y的值,即可得到动点P的坐标.
【解答】
解:(1)∵直线y=kx+6过点E(−8,0),
∴ 0=−8k+6,
∴ k=34.
(2)∵点A的坐标为(−6,0),
∴ OA=6,
∵点P(x,y)是第二象限内的直线上的一个动点,
∴ΔOPA的面积:S=12×6×(34x+6)=94x+18.
∵94x+18>0,且x<0.
∴ x∈(−8,0)
∴S=94x+18 ,x∈(−8,0).
(3)由函数关系式令x=0,得到y=6.
ΔOEF的面积S=12×8×6=24,
由ΔOPA的面积是ΔOEF的23,得到ΔOPA的面积为S=24×23=16.
令S=94x+18=16,解得x=−89.
当x=−89时,y=34×(−89)+6=163.
所以当点P的坐标为(−89,163)时,ΔOPA的面积为16.
第21页 共22页 ◎ 第22页 共22页