- 2021-10-27 发布 |
- 37.5 KB |
- 3页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
三角形的中位线教案1
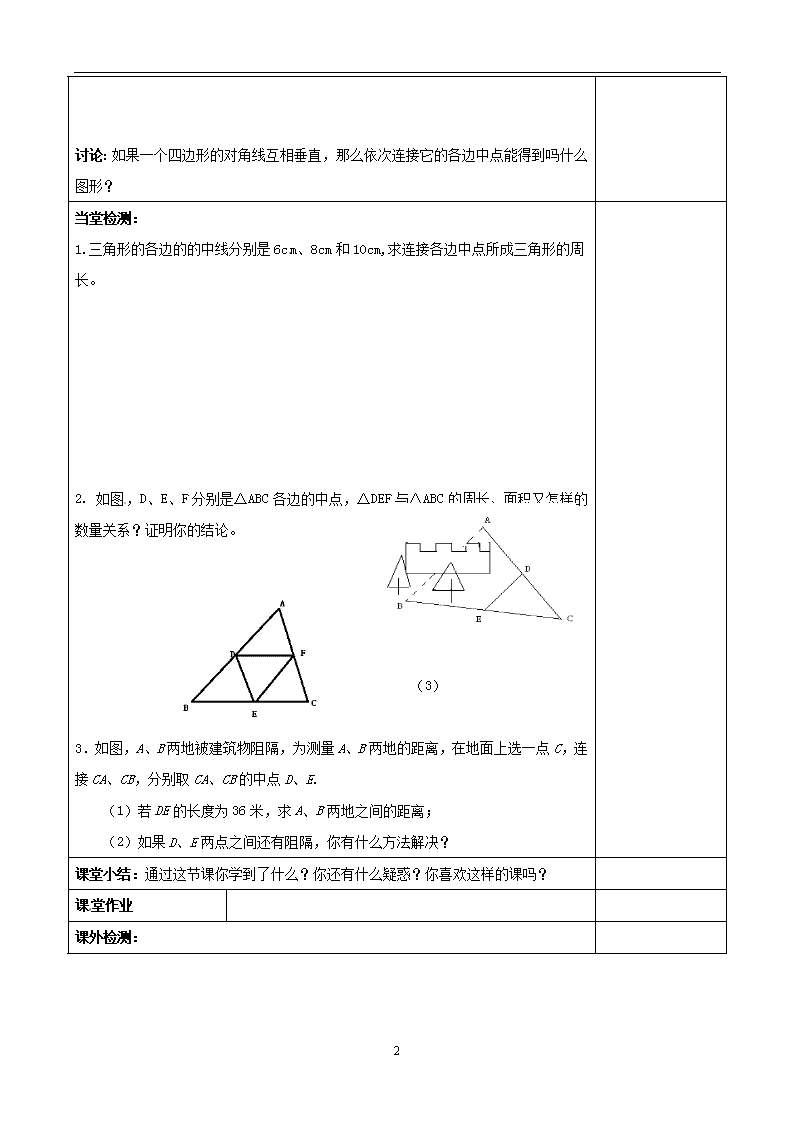
三角形的中位线 教学目标 1.探索并掌握三角形的中位线的概念、性质。 2.会利用三角形中位线的性质解决有关问题。 3.经历探索三角形中位线性质的探索过程,发展学生观察能力及抽象思维能力。 教学重点 探索并掌握三角形中位线的概念、性质 教学难点 三角形中位线的性质的灵活运用 教学过程 二次备课、设计思路 合作交流: 1.动手操作 ①剪一个三角形记为△ABC; ②分别取AB、AC的中点D、E,连接DE; ③沿DE将△ABC剪成两部分,将△ADE绕点E旋转180°,得四边形BCFD,如右图: ④四边形BCFD是平行四边形吗?请说明理由。 ⑤还有什么发现? 2.说一说三角形的中线与三角形的中位线的区别。 3.根据图中的条件,回答问题。 (1)如图(a),已知D、E分别为AB和AC的中点,DE=5,求BC的长。 (2)如图(b),D、E、F分别为AB、AC、BC的中点,AC=8,∠C=70°,求DF的长和∠EDF的度数。 (3)如图(c ),若△DEF的周长为10cm,求△ABC的周长; 若△ABC的面积等于20cm,求△DEF的面积。 (a) (b) (c) 4.例1: 如图,在四边形ABCD中,AC=BD,E、F、G、H分别是AB、BC、CD、DA的中点。求证:四边形EFGH是菱形 3 讨论:如果一个四边形的对角线互相垂直,那么依次连接它的各边中点能得到吗什么图形? 当堂检测: 1.三角形的各边的的中线分别是6cm、8cm和10cm,求连接各边中点所成三角形的周长。 2. 如图,D、E、F分别是△ABC各边的中点,△DEF与△ABC的周长、面积又怎样的数量关系?证明你的结论。 (3) 3.如图,A、B两地被建筑物阻隔,为测量A、B两地的距离,在地面上选一点C,连接CA、CB,分别取CA、CB的中点D、E. (1)若DE的长度为36米,求A、B两地之间的距离; (2)如果D、E两点之间还有阻隔,你有什么方法解决? 课堂小结:通过这节课你学到了什么?你还有什么疑惑?你喜欢这样的课吗? 课堂作业 课外检测: 3 4.顺次连结下列各四边形中点所得的四边形是矩形的是---------------( ) A.等腰梯形 B.矩形 C.平行四边形 D.菱形或对角线互相垂直的四边形 5.已知△ABC中,D是AB上一点,AD=AC,AE⊥CD,垂足是E、F是BC的中点,试说明BD=2EF。 6.如图,四边形ABCD中,AB=CD,M、N分别是AD、BC的中点,延长BA、NM、 CD分别交于点E、F。试说明∠BEN=∠NFC。(提示:连结AC并取中点)。 3查看更多