巩固练05一次函数-2020年【衔接教材·暑假作业】八年级数学（人教版）（解析版） (8)

巩固练05一次函数-2020年【衔接教材·暑假作业】八年级数学（人教版）（解析版） (8)

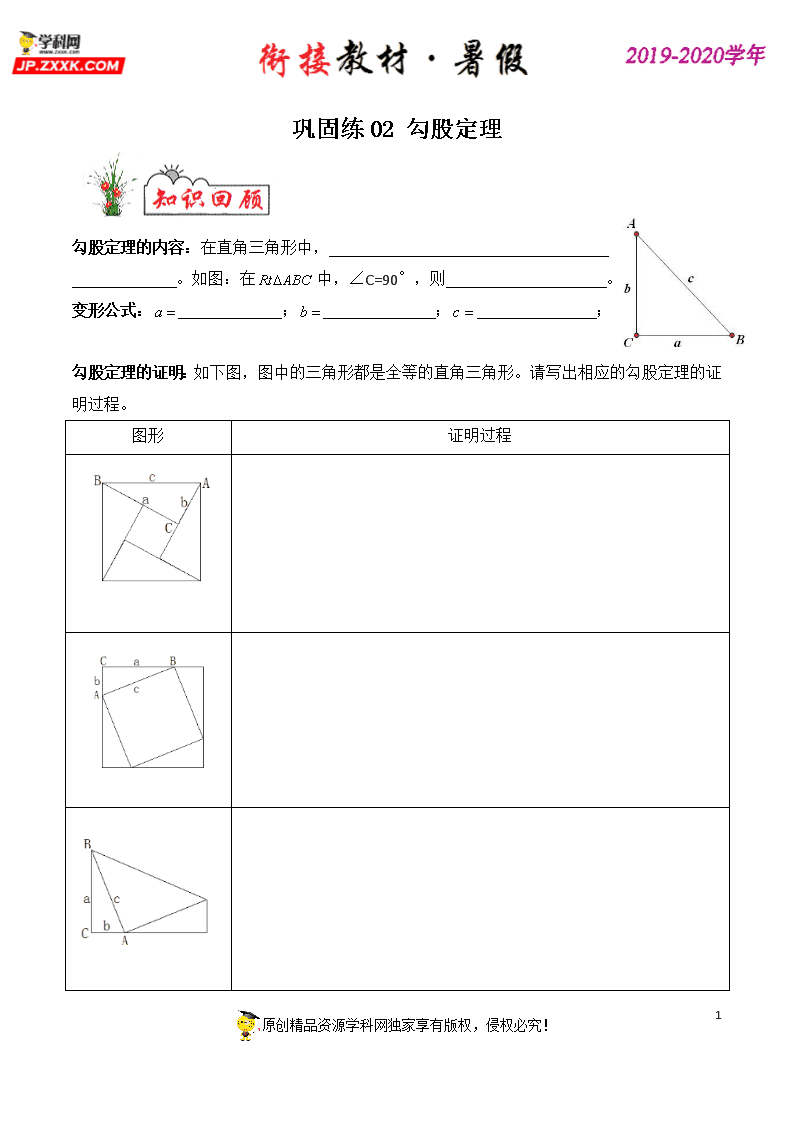
巩固练02 勾股定理 勾股定理的内容：在直角三角形中， ‎ ‎ 。如图：在中，∠C=90°，则 。‎ 变形公式： ； ； ；‎ 勾股定理的证明：如下图，图中的三角形都是全等的直角三角形。请写出相应的勾股定理的证明过程。‎ 图形 证明过程 5‎ 原创精品资源学科网独家享有版权，侵权必究！‎ 定理的定义：经过证明被确认为正确的命题叫做定理。‎ 互逆命题的定义：明天有题设和结论。我们把 、 正好相反的两个命题叫做互逆命题。‎ 互逆定理的定义：如果一个定理的逆命题也是正确的，则它也是一个定理。我们把这两个定理称之为 。‎ 勾股定理的逆定理：在任意三角形中，若三角形的三边分别是，且满足 ，则这个三角形一定是 。且直角边是 ，斜边 。‎ 勾股数：满足 的三个整数叫做勾股数。例如： 。‎ 直角三角形的判定方法：①三角形中有一个角是 的三角形是直角三角形。‎ ‎ ②三角形中有两个角的和是 的三角形是直角三角形。‎ ‎ ③三角形的三边满足 的三角形是直角三角形。‎ ‎1．下列条件中，使△ABC不是直角三角形的是（　　）‎ A． B． ‎ C． D．‎ ‎2．已知△ABC的三边为，下列条件不能判定△ABC为直角三角形的是（　　）‎ A． B．‎ C． D．‎ ‎3．如图，以直角三角形的一条直角边和斜边为一边作正方形M和N，它们的面积分别为9平方厘米和25平方厘米，则直角三角形的面积为（　　）‎ A．6平方厘米 B．12平方厘米 C．24平方厘米 D．3平方厘米 4. 如图，分别以Rt△ABC的三条边为边向外作正方形，面积分别记为S1，S2，S3．‎ 若S1＝36，S2＝64，则S3＝（　　）‎ A．8 B．10 C．80 D．100‎ 5‎ 原创精品资源学科网独家享有版权，侵权必究！‎ ‎5．在Rt△ABC中，，则AB的长是（　　）‎ A． B．2 C．1 D．‎ ‎6．如图，矩形ABCD中，AB＝3，AD＝1，点A，B在数轴上，若以点A为圆心，对角线AC的长为半径作弧交数轴的正半轴于点M，则点M表示的数为（　　）‎ A． B． C． D．‎ ‎7．如图，Rt△ACB中，∠ACB＝90°，AB＝13cm，AC＝5cm，动点P从点B出发沿射线BC以2cm/s的速度运动，设运动时间为ts，当△APB为等腰三角形时，t的值为（　　）‎ A． B．‎ C． D．‎ ‎8．如图，四边形ABCD中，AB＝4，BC＝，CD＝，AD＝4，∠A＝90°，则∠ADC的度数为（　　）‎ A．120° B．105° C．135° D．125°‎ ‎ 第6题 第7题 第8题 ‎9．若点P（a，﹣3）在第四象限，且到原点的距离是5，则a＝　 　．‎ ‎10．图中阴影部分是一个正方形，则此正方形的面积为　 　．‎ ‎ 第10题 ‎11．已知一个直角三角形的两条直角边的长分别是cm和cm，则这个直角三角形的周长为　 　．‎ ‎12．三角形两边分别是6和8，要使这个三角形是直角三角形，则第三条边长是　 　．‎ ‎13．如图，一架长为4m的梯子，一端放在离墙脚3m处，另一端靠墙，则梯子顶端离墙脚　 　．‎ 5‎ 原创精品资源学科网独家享有版权，侵权必究！‎ ‎14．把图1中长和宽分别为3和2的两个全等矩形沿对角线分成四个全等的直角三角形，将这四个全等的直角三角形拼成图2所示的正方形，则图2中小正方形ABCD的面积为　 　．‎ ‎15．如图所示，一根长为7cm的吸管放在一个圆柱形杯中，测得杯的内部底面直径为3cm，高为4cm，则吸管露出在杯外面的最短长度为　 　cm．‎ ‎16．如图，一座城墙高11.7米，墙外有一个宽为9米的护城河，那么一个长为15米的云梯　 　（填“能”或“否”）到达墙的顶端．‎ ‎ 第14题 第15题 第16题 ‎17．在一条东西走向河的一侧有一村庄C，河边原有两个取水点A，B，其中AB＝BC，由于某种原因，由C到B的路现在已经不通，该村为方便村民取水决定在河边新建一个取水点D（A、D、B在同一条直线上），并新修一条路CD，测得CA＝6.5千米，CD＝6千米，AD＝2.5千米．‎ ‎（1）问CD是否为从村庄C到河边最近的路？请通过计算加以说明；‎ ‎（2）求原来的路线BC的长．‎ ‎18．如图，小明将升旗的绳子拉到旗杆底端，并在绳子上打了一个结，然后将绳子拉到离旗杆底端9米处，发现此时绳子底端距离打结处约3米，请算出旗杆的高度．‎ 5‎ 原创精品资源学科网独家享有版权，侵权必究！‎ ‎19．如图，在四边形ACBD中，AC＝6，BC＝8，AD＝，BD＝，DE是△ABD的边AB上的高，且DE＝4，求△ABC的边AB上的高．‎ ‎20．如图，在两面墙之间有一个底端在A点的梯子，当它靠在左侧墙上时，梯子的顶端在B点；当它靠在右侧墙上时，梯子的顶端在D点．已知∠BAC＝60°，∠DAE＝45°，点D到地面的垂直距离DE＝．‎ ‎（1）求梯子的长度；‎ ‎（2）求BC和CE的长度．‎ 5‎ 原创精品资源学科网独家享有版权，侵权必究！‎