- 2021-10-27 发布 |
- 37.5 KB |
- 10页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
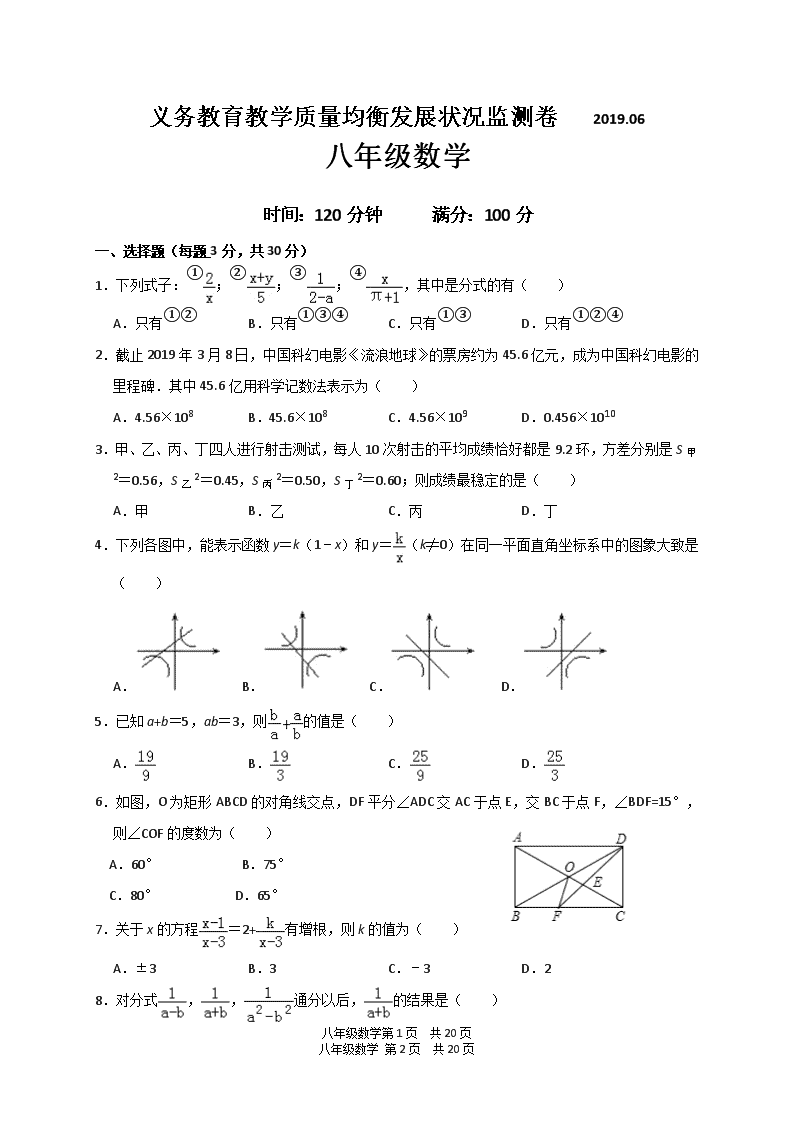
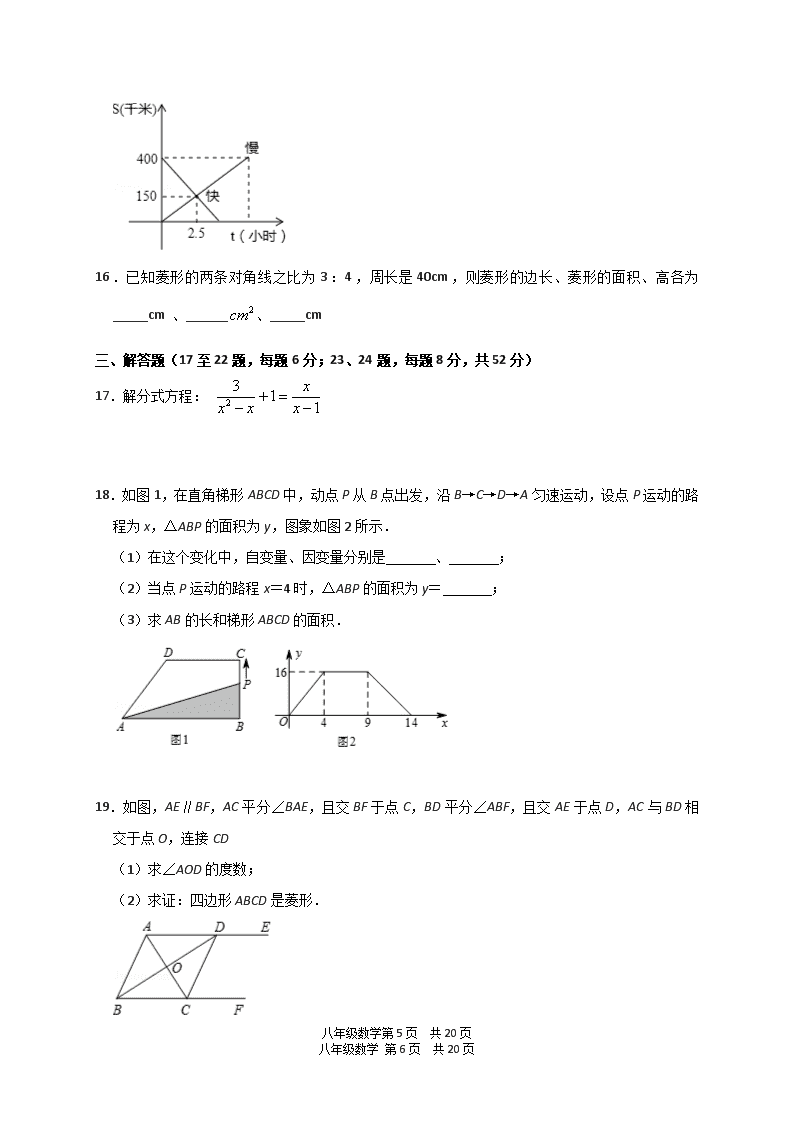
四川省攀枝花市米易县2018-2019学年八年级下学期期末监测数学试题
义务教育教学质量均衡发展状况监测卷 2019.06 八年级数学 时间:120分钟 满分:100分 一、选择题(每题3分,共30分) 1.下列式子:①;②;③;④,其中是分式的有( ) A.只有①② B.只有①③④ C.只有①③ D.只有①②④ 2.截止2019年3月8日,中国科幻电影《流浪地球》的票房约为45.6亿元,成为中国科幻电影的里程碑.其中45.6亿用科学记数法表示为( ) A.4.56×108 B.45.6×108 C.4.56×109 D.0.456×1010 3.甲、乙、丙、丁四人进行射击测试,每人10次射击的平均成绩恰好都是9.2环,方差分别是S甲2=0.56,S乙2=0.45,S丙2=0.50,S丁2=0.60;则成绩最稳定的是( ) A.甲 B.乙 C.丙 D.丁 4.下列各图中,能表示函数y=k(1﹣x)和y=(k≠0)在同一平面直角坐标系中的图象大致是( ) A. B. C. D. 5.已知a+b=5,ab=3,则的值是( ) A. B. C. D. 6.如图,O为矩形ABCD的对角线交点,DF平分∠ADC交AC于点E,交BC于点F,∠BDF=15°,则∠COF的度数为( ) A.60° B.75° C.80° D.65° 7.关于x的方程=2+有增根,则k的值为( ) A.±3 B.3 C.﹣3 D.2 8.对分式,,通分以后,的结果是( ) 八年级数学第19页 共20页 八年级数学 第20页 共20页 A. B. C. D. 9.如图,正方形ABCD的对角线AC、BD相交于点O,E是AC上的一点,且AB=AE,过点A作AFBE,垂足为F,交BD于点G.点H在AD上,且EH∥AF.若正方形ABCD的边长为2,下列结论: ①OE=OG;②EH=BE; ③AH=2-2;其中正确的有( ) A.①③ B.②③ C.①② D.①②③ 10.如图,两个反比例函数y=和y=在第一象限内的图象分别是C1 和C2,设点P在C1上,PA⊥x轴于点A,交C2于点B,则△POB的面积为( ) A.1 B.2 C.4 D.无法计算 C1 C2 二、填空题(每题3分,共18分) 11.已知反比例函数,那么k的值是 . 12.计算:(3.14﹣)0+(﹣3)2= . 13.用换元法解方程+=﹣时,如果设y=,那么原方程可化成关于y的整式方程,这个整式方程是 . 14.如图,若在象棋盘上建立平面直角坐标系xOy,使“帥”的坐标为(﹣1,﹣2),“馬”的坐标为(2,﹣2),则“兵”的坐标为 . 15.一列快车从甲地开往乙地,一列慢车从乙地开往甲地,两车同时出发,两车离乙地的距离s(千米)与行驶时间(小时)的关系如图所示,则快车的速度比慢车快 千米/时. 八年级数学第19页 共20页 八年级数学 第20页 共20页 16.已知菱形的两条对角线之比为3:4,周长是40cm,则菱形的边长、菱形的面积、高各为_____cm 、______、_____cm 三、解答题(17至22题,每题6分;23、24题,每题8分,共52分) 17.解分式方程: 18.如图1,在直角梯形ABCD中,动点P从B点出发,沿B→C→D→A匀速运动,设点P运动的路程为x,△ABP的面积为y,图象如图2所示. (1)在这个变化中,自变量、因变量分别是 、 ; (2)当点P运动的路程x=4时,△ABP的面积为y= ; (3)求AB的长和梯形ABCD的面积. 19.如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,AC与BD相交于点O,连接CD (1)求∠AOD的度数; (2)求证:四边形ABCD是菱形. 八年级数学第19页 共20页 八年级数学 第20页 共20页 20.如图,在正方形ABCD中,G是CD边上任意一点,连结BG,作AE⊥BG于点E,CF⊥BG于点F. (1)求证:BE=CF. (2)若BC=5,CF=3,求EF的长. 21.先化简,再求值. (1+)÷,其中x=﹣5. 22.如图,在 ABCD中,E,F为对角线BD上的两点,且∠DAE=∠BCF. 求证:(1)AE=CF; (2)四边形AECF是平行四边形. 八年级数学第19页 共20页 八年级数学 第20页 共20页 23.已知一次函数的图象经过A(2,8),B(0,4)两点. (1)求一次函数的表达式. (2)在x轴上是否存在一点P,使得△AOP是等腰三角形?如果存在,请求出点P的坐标;如果不存在,请说明理由. 八年级数学第19页 共20页 八年级数学 第20页 共20页 24.如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标为(4,2),过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N. (1)求直线DE的解析式和点M的坐标; (2)求△OMN的面积; (3)若反比例函数y=(x>0)的图象与△MNB有公共点,请直接写出m的取值范围. 八年级数学第19页 共20页 八年级数学 第20页 共20页 八年级数学参考答案 一.选择题(每小题3分,共30分) 1.C 2.C 3.B 4.D 5.B 6.B 7.D 8.B 9.D 10.A 二.填空题填空题(每小题3分,共18分) 11.±2 12.10 13.2y2+7y+6=0 14.(﹣3,1) 15.40 16.10,96,9.6 三.解答题解答题(17、18、19、20、21、22每小题6分,23、24每小题8分,共52分) 17.解:方程两边都乘x(x﹣1),得 3+x2﹣x=x2, 解得x=3 3分 检验:当x=3时,x(x﹣1)=6≠0, ∴原分式方程的解为x=3. 6分 18.解:(1)x,y; 2分 (2)16; 4分 (3)根据图象得:BC=4,此时△ABP为16, ∴AB•BC=16,即×AB×4=16, 解得:AB=8; 5分 由图象得:DC=9﹣4=5, 则S梯形ABCD=×BC×(DC+AB)=×4×(5+8)=26. 6分 19.解:(1)∵AC、BD分别是∠BAD、∠ABC的平分线, ∴∠DAC=∠BAC,∠ABD=∠DBC, ∵AE∥BF, ∴∠DAB+∠CBA=180°, ∴∠BAC+∠ABD=(∠DAB+∠ABC)=×180°=90°, ∴∠AOD=90°; 3分 (2)证明:∵AE∥BF, 八年级数学第19页 共20页 八年级数学 第20页 共20页 ∴∠ADB=∠DBC,∠DAC=∠BCA, ∵AC、BD分别是∠BAD、∠ABC的平分线, ∴∠DAC=∠BAC,∠ABD=∠DBC, ∴∠BAC=∠ACB,∠ABD=∠ADB, ∴AB=BC,AB=AD ∴AD=BC, ∵AD∥BC, ∴四边形ABCD是平行四边形, ∵AD=AB, ∴四边形ABCD是菱形. 6分 20.解:(1)在正方形ABCD中,BC=AB,∠ABC=90°. ∵AE⊥BG,CF⊥BG, ∴∠ABE+∠CBE=90°,∠ABE+∠BAE=90°. ∴∠CBE=∠BAE. ∴△BCF≌△ABE(AAS). ∴BE=CF; 3分 (2)在Rt△BCF中,BF==4. ∵BE=CF=3, ∴EF=BE﹣BF=1. 6分 21.解:原式=•=, 3分 当x=﹣5时,原式=; 6分 22.证明:(1)∵四边形ABCD是平行四边形, ∴AB=CD,AB∥CD,∠DAB=∠BCD. ∵∠DAE=∠BCF, ∴∠ABE=∠CDF,∠BAE=∠DCF. 在△ABE和△CDF中, 八年级数学第19页 共20页 八年级数学 第20页 共20页 , ∴△ABE≌△DCF(ASA). ∴AE=CF. 3分 (2)∵△ABE≌△DCF, ∴∠AEB=∠CFD, ∴∠AEF=∠CFE, ∴AE∥CF, ∵AE=CF, ∴四边形AECF是平行四边形. 6分 23.解:(1)∵B(0,4), ∴设直线AB的表达式为y=kx+4, ∵A(2,8)在此直线上, ∴2k+4=8,∴k=2, ∴直线AB的表达式为y=2x+4; 2分 (2)存在, 设点P(m,0), ∵A(2,8),O(0,0), ∴OP2=m2,OA2=68,AP2=(m﹣2)2+64, ∵△AOP是等腰三角形, ∴①当OP=OA时,m2=68, ∴m=±2, ∴P(2,0),或(﹣2,0) 4分 ②当PO=PA时,m2=(m﹣2)2+64, ∴m=17, ∴P(17,0) 6分 ③当AO=AP时,68=(m﹣2)2+64, ∴m=0(舍)或m=4, ∴P(4,0), 8分 即:满足条件的点P的坐标为P(2,0),或(﹣2,0)或(17,0)或(4,0). 八年级数学第19页 共20页 八年级数学 第20页 共20页 24.解:(1)设直线DE的解析式是y=kx+b, 根据题意得:, 解得:, 则直线DE的解析式是:y=﹣x+3, 2分 令y=2,得到2=﹣x+3,解得:x=2,则M的坐标是(2,2); 3分 (2)把x=4代入y=﹣x+3,解得y=1,则N(4,1), ∴MN==, 则△OMN的面积S=S矩形OABC﹣S△OAM﹣S△BMN﹣S△OCN=2×4﹣﹣﹣=8﹣2﹣1﹣2=3, 6分 (3)经过M的反比例函数的解析式是:y=,同时经过点N, 经过点B的反比例函数的解析式是:y=, 则反比例函数y=(x>0)的图象与△MNB有公共点时, k的范围是:4≤k≤8. 8分 八年级数学第19页 共20页 八年级数学 第20页 共20页查看更多